基于层次分析法和物元分析的拉月滑坡稳定性评估

张 孟 帅

(西南交通大学土木工程学院，四川 成都 610031)

1 概述

拉月滑坡位于林芝县排龙乡东久河左岸上，川藏线测设里程K4108+250～K4108+800，路线长550 m。1967年在东久河左岸发生山体滑坡，超过千万方的物质从坡体剪出，堵塞东久河，形成拉月大滑坡[1,2]。在此事件发生后，除堵江坝体被河流冲走，其他滑坡体堆积于坡体中下部，在坡体上形成以崩塌、滑坡、残坡积体共存的复合堆积体斜坡，该堆积体存在结构松散、强度较低、固结性差的问题，在外界诱发因素作用下可能会产生滑动。因此，基于对川藏铁路选线风险调控的实际需求，需对拉月滑坡稳定性发展趋势进行评价，即对拉月松散堆积体斜坡再次发生滑动的风险进行评估。

2 评估体系的确定

影响坡体稳定性指标因素较多，且他们之间的具体影响权重尚无准确数值给出，只能相对去比较因素之间的作用强度，那就需要我们在主观赋权法中选择一个合适的方法。其中层次分析法作为主观赋权法的一种，具有系统性分析、简洁实用、所需定量信息少的优点，与坡体稳定性分析所需条件较为匹配，因此本文采用层次分析法计算各指标的权重。

2.1 评估体系的建立

在应用层次分析法解决各类决策问题时，需把复杂问题分解为对应组成元素，并按照元素属性不同自上而下分解成若干层。同一层元素对上层元素为从属关系，对下层元素为支配作用，然后根据分层情况建立一个递阶层次结构评价模型[3]。

在对坡体进行风险评估时，我们需要选取客观公正的指标去反映坡体的实际情况，基于此原则，结合工程资料采用层次分析法将坡体稳定性分析分为三个层次，分别为目标层、准则层和方案层。主要从坡体总特征、形态特征、结构特征和诱发因素四个子系统对坡体进行分析，我们构建如表1所示的指标体系。

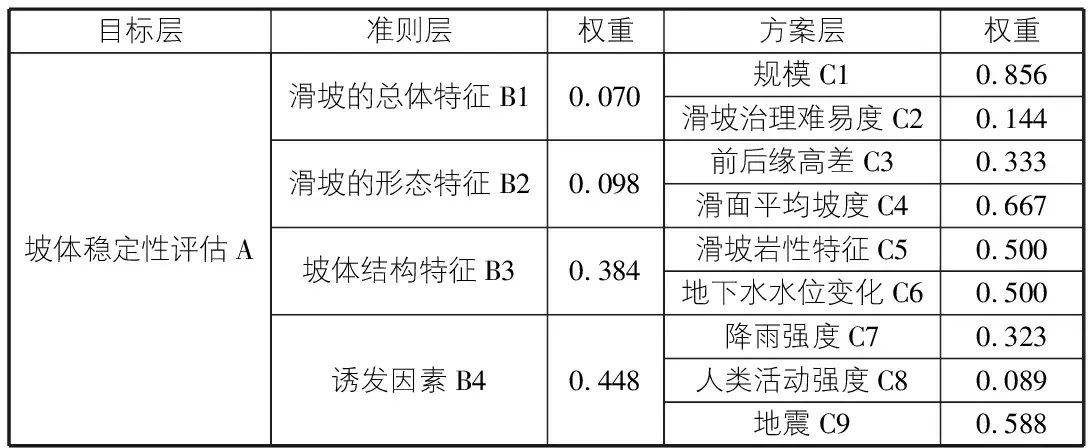
表1 坡体稳定性分析指标体系

2.2 确定评估体系权重

确定好体系之后，接着根据专家意见对同层元素两两进行对比，构建判断矩阵。其次对层次进行单排序和一致性检验，求得最大特征根和特征向量，最后确定各指标权重。根据专家调查表中每位专家所给标度，分别建立判断矩阵，再将所有的判断矩阵所求出的权重值算术平均，得到总的评价权重值[4]。例如，根据其中一位专家所给标度，可建立如下判断矩阵，准则层判断矩阵如表2所示。

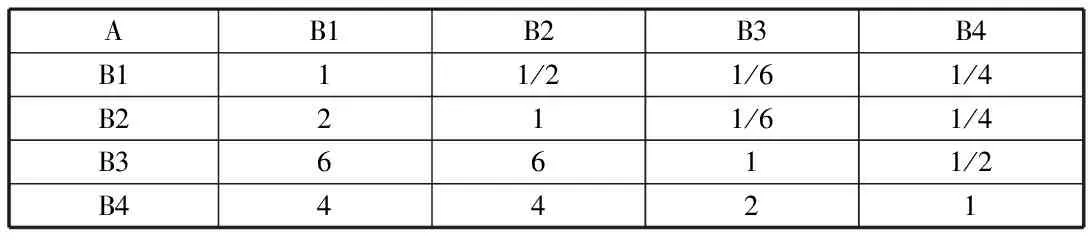
表2 准则层判断矩阵

由此判断矩阵可得：

一致性检验指标：

准则层的权重分别B1=0.070；B2=0.098；B3=0.384；B4=0.448。

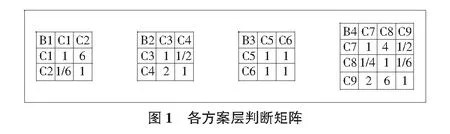
同理可得到该专家给定的各方案层判断矩阵，如图1所示。进而求得各方案层的权重，即可得准则层和方案层各层的权重,如表1所示。

3 物元分析

采用物元分析对某一事件的评价应用较多，如梁川采用物元分析对水质量评价[5]；李祚泳利用物元分析对自然灾害灾情进行评估等[6]。但目前尚未应用于坡体稳定性风险评估中，基于此，我们采用其对坡体稳定性进行综合评价，并探究其在灾害稳定性评判和减灾策略上应用。

3.1 物元分析的基本概念

物元分析是一种介于数学和实验科学的新学科，由我国学者蔡文在论文《可拓集合和不相容问题》中首次提出物元分析，该方法通过促进事物转化以解决不相容问题，并与创造思维学有着紧密的联系[7]。我们可利用物元分析方法，建立基于事物多指标的质量评定模型，并对指标参数进行定量分析最终以定量的数值表示评定结果。

由N，c，v构成有序的三元组R=(N,c,v)即为描述事物的基本元，简称物元。其中，N为给定事物；c为事物具有的特征；v为特征的量值；则N，c和v称为物元R的三要素。

3.2 计算过程

物元分析方法主要有以下几步：

1)确定经典域、节域和待识别的对象形成的物元。

经典域即选定对象、指标、指标标准值区间的分级，节域即选定的评价对象、指标、指标标准值的所有范围，待评物元即关于检测所得的具体数据。

2)确定权重。

3)建立关联函数，计算关联函数值。

4)关联度及评定等级。

4 坡体稳定性风险评估

4.1 经典域、节域的确定

本文选取了滑坡规模、滑坡治理难易度、前后缘高差、平均坡度、岩性、地下水水位、降雨量、人类活动强度和地震九项指标，根据该流域历史数据对这九个因素间的量值进行划分，其中岩性、滑坡治理难易度、人类活动强度这三个指标根据实际情况由专家给出定量化评估。对于地下水水位变化对坡体稳定性影响，依据刘明发在地下水对坡体稳定性影响中的结论，水位在0 m～20 m区间内增长时，边坡稳定系数一直在下降，水位在0 m～6 m变化时，对坡体稳定性影响最小，且边坡稳定系数最高，当在6 m～10 m变化时对坡体稳定性影响增大，10 m～15 m时稳定性影响下降趋势开始变缓，当地下水位为20 m时，稳定系数最低[8]。本文将坡体稳定状态分为非常安全、较安全、偶然不安全、较不稳定、不稳定五个等级，对于各个指标在五种等级中的取值范围主要依据各项指标在该变化范围内对坡体的影响程度不同进行划分，得到如表3所示的等级划分，即确定滑坡风险评估中的经典域和节域。

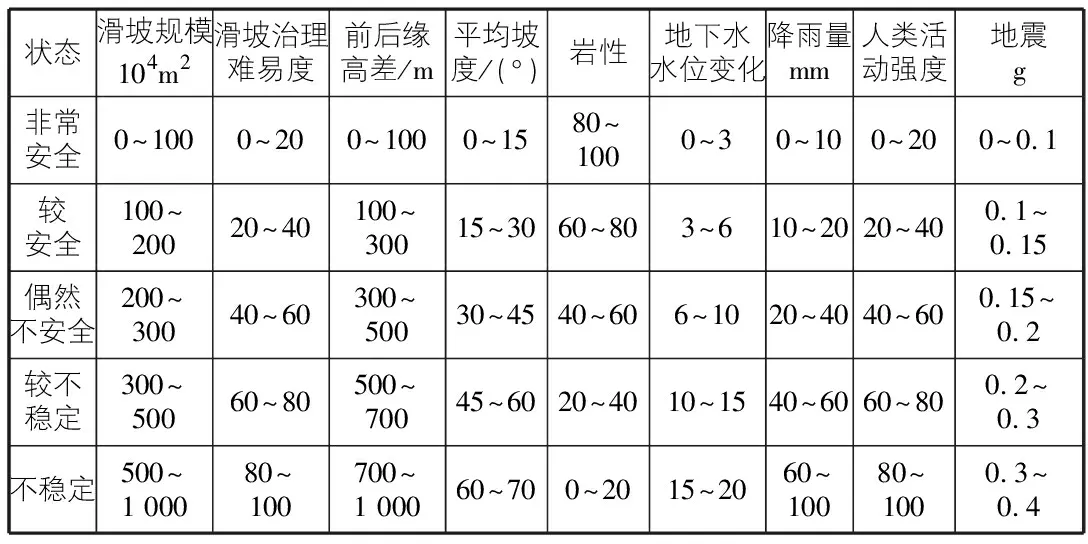
表3 拉月滑坡评价指标及标准划分

进而得到经典物元矩阵和节域物元矩阵如下所示：

表4 拉月滑坡评价归一化指标及标准划分

4.2 拉月滑坡目前状态

拉月滑坡在1967年发生滑动后，其原有状态已经改变，原滑坡体下滑堆积在坡体下部，使得坡体下部变厚，堆积滑坡体体积约为200×104。坡度变缓，坡度为30°左右，堆积层前后缘高差349 m。在雨季平均单日降雨量影响下，地下水位上升为2.1 m。每年8月份～10月份，冰川仍在消融期，且处在降雨期，我们依照波密气象站记录的数据为依据，选取其12 h降雨量为30 mm。该区域位于强地震影响区，其地震动峰值加速度为0.20g，相当于地震基本烈度8度[1]。对于拉月滑坡坡体，经过专家评审给出的岩性得分为45分，滑坡治理得分为50分，人类活动得分为30分。我们得到九项指标数据如表5所示，并对其进行了归一化处理。

表5 指标值及其归一化值

根据上述物元分析计算过程，我们得出各项指标的等级关联度，如表6所示。

表6 关联度计算结果

结合采用层次分析法求得的九项指标的权重值，进而求得坡体目前状态与五个等级之间的隶属度关系，如表7所示。

表7 综合关联度计算结果

由上述计算结果可知，拉月滑坡坡体在雨季12 h降雨量30 mm(暴雨水平)的情况下，坡体会处于偶然不安全状态，有触发滑坡的风险，此时会随着降雨时长增加和降雨量的增加，致使坡体出现滑动的可能性变大。斜坡也可能在强地震动力响应下产生崩滑灾害。故其在天然状态下自稳情况相对较好，在无强烈地震或极端降雨，大型人类工程活动等外界条件的激发下，坡体不会出现大的整体滑动。

5 结语

1)在应用物元分析对坡体稳定性进行风险评估时，计算方法简单便捷，关联度真实反映了坡体目前的状态，与实际较为接近。并采用层次分析法计算指标权重，具有逻辑性强实用性好的优点，并能准确得出各指标权重值。

2)拉月滑坡堆积体在降雨、地震诱发因素作用下其危险性处于偶然不安全状态，说明拉月滑坡体在天然条件下相对稳定，但在极端降雨、地震等诱发因素作用下，滑坡仍有一定的发生可能性，若线路经过该区域，需对坡体进行综合治理。