基于依赖频率AVO反演的高含气饱和度储层预测方法

罗 鑫 陈学华 张 杰 蒋 伟 孙雷鸣 肖 为

(①成都理工大学地球勘探与信息技术教育部重点实验室，四川成都 610059； ②成都理工大学油气藏地质及开发工程国家重点实验室，四川成都 610059； ③中海油田服务股份有限公司物探事业部特普公司，广东湛江 524057)

0 引言

有效预测高含气饱和度储层对于勘探、开发具有重要意义，但预测储层的含气饱和度难度较大。由常规的叠前或叠后反演得到的弹性参数对含气饱和度的敏感性很弱，因此寻求对含气饱和度敏感的流体因子势在必行。

传统的AVO分析技术基于Zoeppritz方程，讨论反射系数与界面上、下地层的纵、横波速度及密度之间的关系，通过地层弹性参数变化对地震振幅的影响预测油气储层[1]。孙鹏远[2]基于AVO理论详细研究了正演模拟、流体替换、弹性参数反演，对AVO储层预测和流体识别具有重要意义。然而，由常规AVO反演技术获得的弹性参数对含气饱和度的敏感性很弱，较难识别高含气饱和度的有效储层。岩石物理观测和多孔介质弹性理论研究发现，地震波穿过饱含流体储层时会产生频散和衰减现象[3-5]，并且频散属性对含气饱和度具有很强的敏感性。如：王峣钧等[6]基于斑块饱和模型分析了地震波频散与含气饱和度的关系；张广智等[7]研究了微观与介观波致流下的速度频散与衰减，并讨论了含水饱和度与频散、衰减的关系；Chen等[8-9]分析了孔隙岩石饱含多相流体时的速度频散和衰减；李世凯等[10-11]基于斑块饱和模型分析了含气饱和度对频散的影响，基于黏滞—弥散理论模拟了含气砂岩的地震响应特征。因此，可充分利用频散特性预测高含气饱和度储层。

常规AVO分析仅利用原始地震反射振幅随入射角的变化，忽略了频率因素，没有考虑不同频率分量的特征参数随入射角变化的差异，不能提取与储层流体有关的地震频散异常。Chapman等[12-14]基于喷射流理论提出了动态等效介质模型，发现由岩石中流体流动引起的频散与衰减效应导致依赖频率的AVO响应，即地震反射系数不仅与入射角有关，且随频率而变。Wilson等[15]、吴小羊[16]将时频分析技术与传统AVO技术相结合，提出依赖频率的AVO技术，Chen等[17]利用该技术模拟了储层流体流度变化所致的地震响应异常；高刚[18]详细分析了含流体孔隙介质的地震响应特征，并利用纵、横波频散属性识别流体；张震等[19]实现了基于Russell反射系数依赖频率的AVO反演；罗鑫等[20]实现了基于Gray反射系数依赖频率的AVO反演；钟晗等[21]分析了依赖频率的AVO的影响因素。上述研究为利用依赖频率的AVO反演提供了技术方法。

Li等[22]、Wu等[23]利用依赖频率的AVO方法，通过数值模拟和实际资料分析定量估算含气饱和度。Chen等[24]基于地震波的频散反演定量计算含气饱和度。上述工作主要基于理论分析与数值模拟，研究了频散、衰减与含气饱和度的关系。

1 方法原理

1.1 Chapman动态等效介质理论

Chapman等[26]基于孔隙介质的喷射流模型，提出了一种喷射局部流模型的理论，该喷射局部流模型考虑了储层孔隙度、渗透率、裂缝密度和方向、孔隙流体特征(流体黏度或黏滞系数)、体积模量和密度等与频率有关的地震各向异性特征，可计算依赖频率的有效矩阵张量，了解频散和衰减特征。基于此模型的有效刚度矩阵为

Cijkl=C0ijkl-φpC1ijkl-εcC2ijkl-εfC3ijkl

(1)

式中：C0表示介质的拉梅系数为λ、μ时的各向同性弹性张量；C1、C2和C3为对应孔隙介质的孔隙度φp、裂隙密度εc和裂缝密度εf的校正弹性张量，这三个校正量均是拉梅系数、流体和裂缝特性、频率及弛豫时间(松弛时间或时间尺度因子)的函数；ijkl为矩阵元素的下标。

(2)

Cijkl(ω)=C0ijkl(Λ,M,ω)-φpC1ijkl(λ0,μ0,ω,τ)-

εcC2ijkl(λ0,μ0,ω,τ)-εfC3ijkl(λ0,μ0,ω,τ)

(3)

计算与频率有关的各向异性弹性张量。式中φp、εc和εf体现了岩石弹性性质的频率依赖性和各向异性特征，可由计算实测速度参数得到。

岩石物理实验证实，孔隙岩石中的流体流动存在颗粒尺度(微裂隙和孔隙)和裂缝尺度，从而出现与松弛时间有关的两个特征频率。颗粒尺度的流体流动对应传统的喷射流频率(或松弛时间τm)；裂缝内外的流体流动则对应较低的特征频率(或很大的松弛时间τf)，由裂缝尺度决定。随着裂缝半径增加，裂缝表面积与其体积比降低，因此流体流动达到压力平衡的时间就越长(松弛时间越大)。两种松弛时间存在以下关系

(4)

式中：af为裂缝半径；ζ为骨架的颗粒尺寸。当纵横比较小时，有

(5)

式中：a为孔隙半径；σ为固体矿物的泊松比；κ为岩石渗透率；μ为剪切模量；η为流体黏度。

式(5)说明η影响τm，而τm与地震波频散和衰减的特征频率有关。因此，η直接影响频散和衰减的变化特征。

通过矩阵张量

(6)

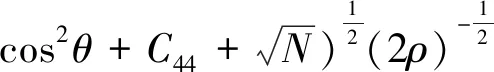
(7)

式中

N= [(C11-C44)sin2θ-(C33-C44)cos2θ]2+

(C13+C44)2sin22θ

(8)

进而可以求得依赖频率的相速度VP(ω)和逆品质因子1/Q(ω)

(9)

1.2 混合流体黏度、密度及体积模量的计算

为了研究随含气饱和度的变化产生的速度频散和能量衰减，引入混合流体黏度计算方法。混合流体黏度的每个分量可用黏度混合数(VBN)表示，给定混合流体各组分的黏度，则计算混和流体黏度的步骤如下。

(1)计算混合流体每个成分的VBN。

VBNi=14.535×ln[ln(ηi+0.8)]+10.975

(10)

式中ηi为运动黏度，是在固定温度和压力条件下测得的。

(2)计算混合流体的VBNm。

(11)

式中xi为第i个流体成分所占的百分比。

(3)计算混合流体的运动黏度η。

(12)

此外，不同饱和度时的流体密度以及饱和砂岩密度为

(13)

式中：ρm、ρf、ρg和ρw分别为岩石骨架、饱和流体、气和水的密度；Sg为含气饱和度；φ为孔隙度。

混合体积模量Kf可以由Wood公式求得

(14)

式中：Kg为气的体积模量；Kw为水的体积模量。

1.3 依赖频率的AVO反演

Russell等推导了基于f-μ-ρ的AVO反射系数近似表达式

(15)

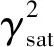
(16)

(17)

则有

(18)

(19)

令

(20)

(21)

与其他参数相比，Δρ/ρ的变化非常小，忽略式(15)中的密度项，并考虑频散效应，形成依赖频率的AVO反演公式

(22)

R(θi,ωi)

(23)

定义

(24)

1.4 谱均衡进行反演优化

在进行依赖频率的AVO反演中，需要消除由于子波效应导致的能量不均衡现象。文中用广义S变换(Generalized S-transform，GST)进行时频谱分析[28]，GST定义式为

(25)

式中：β、p为调节因子；x(t)为原始信号；F为频率。

某个n道的地震道集可以表示为s(t,n)，对其进行广义S变换可以求得不同频率的瞬时谱Sωi(t,n)。为了消除瞬时谱中的子波效应，利用谱均衡的方法对所有的频率成分加权求和求取加权因子，其表达式为

(26)

式中：Sω0(n)是接收道为n、参考角频率为ω0的瞬时振幅谱；Sωi(n)是接收道为n、角频率为ωi的瞬时振幅谱。利用式(26)得到加权函数，然后对叠前AVO道集的瞬时谱进行谱均衡处理

(27)

依赖频率AVO反演的流程如图1所示。

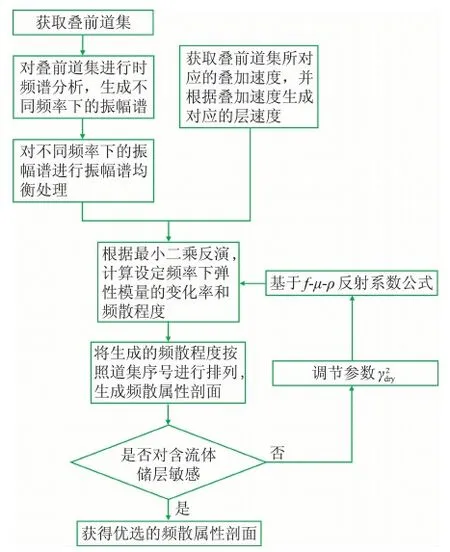
图1 依赖频率的AVO反演流程图

2 数值模拟

2.1 地震响应的数值计算方法

利用与频率、时间尺度因子等参数有关的弹性张量计算依赖频率的纵横波速度参数VP(ω)和VS(ω)，基于Wiggins等[29]提出的AVO三项线性近似公式，将其拓展至入射角—频率域，可建立依赖频率的AVO反射系数分布

RP(ω,θ)=A(ω)+B(ω)sin2θ+C(ω)tan2θsin2θ

(28)

其中

(29)

式中：VP(ω)和VS(ω)分别为界面两侧介质依赖频率的纵、横波速度的均值； ΔVP(ω)和ΔVS(ω)分别为界面两侧介质依赖频率的纵、横波速度的差值；ρ为界面两侧介质密度的均值； Δρ为界面两侧介质密度的差值。

由上述公式可以得到依赖频率的反射系数，结合得到的依赖频率的速度，由相移法波动方程正演模拟得到依赖频率的合成角道集。在此采用一维波动方程

(30)

式中：u为介质的标量位移；V为依赖频率的纵波速度。

对于平面波有

u=e-ikzzei ω t

(31)

将式(31)代入式(30)，并对t做傅里叶变换，可得到与V(ω)有关的垂直波数表达式

(32)

利用频率—波数域相移法[30]进行波场延拓，即可完成数值模拟，相移式为

u(z+Δz,ω)=u(z,ω)eikz(ω)Δz

(33)

从而可获得依赖频率的AVO响应。

2.2 模型试算

文中讨论储层含气和含水两种情况，设计四层地质模型(图2)，其中第二层饱含流体。分析不同含水饱和度的依赖频率的地震响应以及频散和衰减，模型参数如表1和表2所示。

首先分析动态黏度随含水饱和度的变化(图3)，结果表明，流体的动态黏度随含水饱和度的增大而增大。基于Chapman动态等效介质理论计算不同含水饱和度的频率—速度以及频率—逆品质因子关系曲线(图4)，结果表明，速度和逆品质因子都是频率的函数，不同含水饱和度的频散和衰减情况不同，随着含水饱和度的增加速度值增大，速度和逆Q值均增大，且特征频率向低频方向移动。因此，利用与含水(含气)饱和度有关的速度频散和衰减信息预测高含气饱和度储层非常有效。

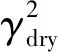
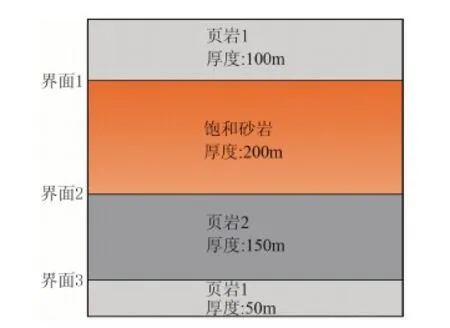
图2 地质模型

物理参数值VP/(m·s-1)2755页岩1VS/(m·s-1)1402ρ/(g·cm-3)2.07VP/(m·s-1)2975页岩2VS/(m·s-1)1595ρ/(g·cm-3)2.20

表2 饱和砂岩参数

注：r为裂隙纵横比

图3 动态黏度随含水饱和度的变化

图4 依赖频率的纵波速度(a)、逆Q(b)

图5 饱气(a)和饱水(b)状态下的地震角道集

图6 不同时的If随时间的变化

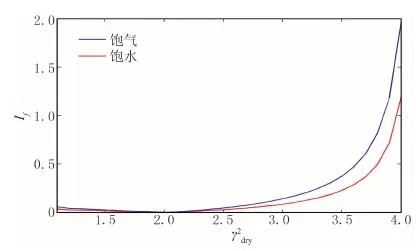
图7 界面3的If值随的变化

3 实际资料分析

为了更好地说明频散因子If对高含气饱和度有效储层的预测效果，选取A区的地震资料进行分析。

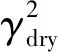
为了进一步对比、分析利用If识别高含气储层的效果，抽取井位处的频散曲线和测井含水饱和度Sw曲线进行对比、分析(图10)。由图可见：If对含水饱和度的敏感性很高，可以更好地区分有效储层，当Sw<60%时，主要为气层，频散异常较大，当Sw>80%时，主要为水层，频散异常较小；而纵波属性Ia对饱和度的敏感性较差，难以区分不同饱和度的储层。因此，利用优选的频散属性If可以更好地识别高含气饱和度有效储层。

图8 A区过井X的叠后剖面(a)及井位处的地震道时频分析结果(b)

图9 频散因子If剖面

图10 井位处频散属性与测井含水饱和度Sw对比

4 结束语

本文引入混合流体黏度的计算方法，分析了含水饱和度与流体黏度的关系以及对频散和衰减的影响，并基于频变AVO反演方法，优选了对流体敏感的频散因子，实现了对高含气饱和度储层的预测，得到以下认识。

(1) 流体黏度会影响松弛时间，并与含水饱和度之间存在密切关系，直接影响速度频散和衰减的变化特征。不同流体的频散和衰减程度不同，并且依赖含水(含气)饱和度的变化。

(2)基于Russell提出的f-μ-ρ反射系数公式，通过依赖频率的AVO反演，得到了对流体敏感的频散因子，并通过谱均衡方法提高了反演精度。

(3)优选的频散属性对流体储层具有很强的敏感性，可识别高含气饱和度储层，且受背景干扰小，并可以精确地刻画高含气饱和度储层的空间分布位置。