基于BP神经网络和SVR的Fundão尾矿坝排水数据预测对比研究*

戴健非，杨 鹏,2，王昕宇

(1.北京联合大学 北京市信息服务工程重点实验室，北京 100101； 2.北京科技大学 土木与资源工程学院，北京 100083)

0 引言

尾矿库是维持矿山企业正常运营的必要设施，由1个或多个尾矿坝堆筑拦截谷口或围地所构成的矿山生产设施，是具有高势能的人造危险源。其稳定性与安全性对矿山企业的正常生产和区域安全至关重要[1-3]。因此，研究尾矿坝溃坝失效的早期预警是很有必要的。在Fundão尾矿坝倒塌1 年后，超过4 300万m3的铁矿石尾矿仍然造成环境破坏，污染了从Doce河流域到大西洋的668 km水道。污染物的数量和受影响的生态系统的范围占据了前所未有的比例，涉及巴西大西洋森林河口，沿海和海洋环境[4]。对溃坝原因调查后发现[5]，尾矿坝由于一系列“施工缺陷”导致了砂土液化。其中，基础排水沟的施工缺陷最为严重，排水系统有缺陷，导致库内尾矿饱和度过高，小型地震诱发溃坝。由此可见，排水能力是否正常在尾矿坝安全领域起着重要的指示作用。本文根据专家小组的数据支持预测排水数据flow即每秒排水量(L/s)。国内外学者在尾矿库安全预警方面做了大量研究。在尾矿坝数据预测方面， Dong等[6]通过考虑潜水线预测方程，极限平衡状态参数，水库水位和降雨量建立数值模拟模型，通过远程实时预警获得尾矿坝稳定或危险的预警信号；王英博等[7]采用修正型果蝇算法优化的BP神经网络对滩顶高度、库水位、浸润线、干滩长度和安全超高5个指标拟合,显示出较高的预测精度；李娟等[8]使用SVM预测尾矿坝浸润线,实现了小样本情况下的高精度预测； Tongle等[9]基于遗传算法和BP神经网络预测尾矿浸润线的未来状态。在尾矿坝安全理论方面，何学秋等[10]经过多次实验得出尾矿坝变形需经历衰减、稳定、加速3个阶段的结论，基于流变-突变理论,分别制定预警准则；王昆等[11]综合分析了国内外尾矿库溃坝灾害防控现状及发展情况；张兴凯等[12]采用物理模型试验方法建立尾矿库漫顶溃坝演化模型，证明了尾矿库洪水漫顶溃坝位移与坝体饱和程度有关，坝体浸润线越高,尾矿库溃坝时滑动位移越大，溃口破坏程度取决于溢流对坝体的冲刷侵蚀作用。在传感器稳定采集数据方面，陈凯等[13]研究了矿山监测系统的防护、供电能力、网络通信等技术,来确保极端天气环境下的数据获取。

为实现尾矿库排水流量数据的实时预测，本文建立基于BP神经网络(Back Propagation Neural Network)和支持向量回归(Support Vector Regression， SVR)的巴西Fundão尾矿坝流量数据的预测回归模型。分析库水位、降雨量和干滩长度对排水数据的影响。本文所述模型可为Fundão坝的溃坝预警提供决策支持，对防止溃坝事故和保护尾矿安全具有参考价值。

1 数据来源与传感器

本文所用数据均来自于文献[5]。

巴西Fundão尾矿坝的流量监测是采用位于海拔826 m处的流量传感器采集得到。在826 m处安装有27个排洪隧洞进行排水，材料为混凝土材质。2011年的ITRB(Independent Tailings Review Board)报告指出，排水系统朝向右侧和左侧基台，但是，只能从右侧基台附近的水槽进行测量[5]。

排水数据监测有每小时排水立方米和每秒排水升数2种计量模式。本文仅采用每秒排水升数作为模型的输出特征，并记为flow。库水位和降雨量来自于小组审查的Samarco现场监测数据。安装的监测仪器类型是振弦式压力计和水位指示器(立管)。主要数据来源是Samarco的月度仪表报告和Samarco电子数据表格。干滩长度数据每月更新1次。数据来源共有4种：月度尾矿排放报告、使用无人机地形测量估算干滩长度及上升率电子表格、每月岩土监测报告和地形测量数据。选取的溃坝灾害数据包含3个特征属性：库水位(m)、降雨量(mm)、干滩长度(m)。本文提取了2011年7月至2015年11月的巴西Fundão坝的上述3种溃坝灾害特征数据和排水数据共62组数据作为数据源。其中，2011年7月至 2015年3月的数据作为训练集，部分历史数据如表1所示。

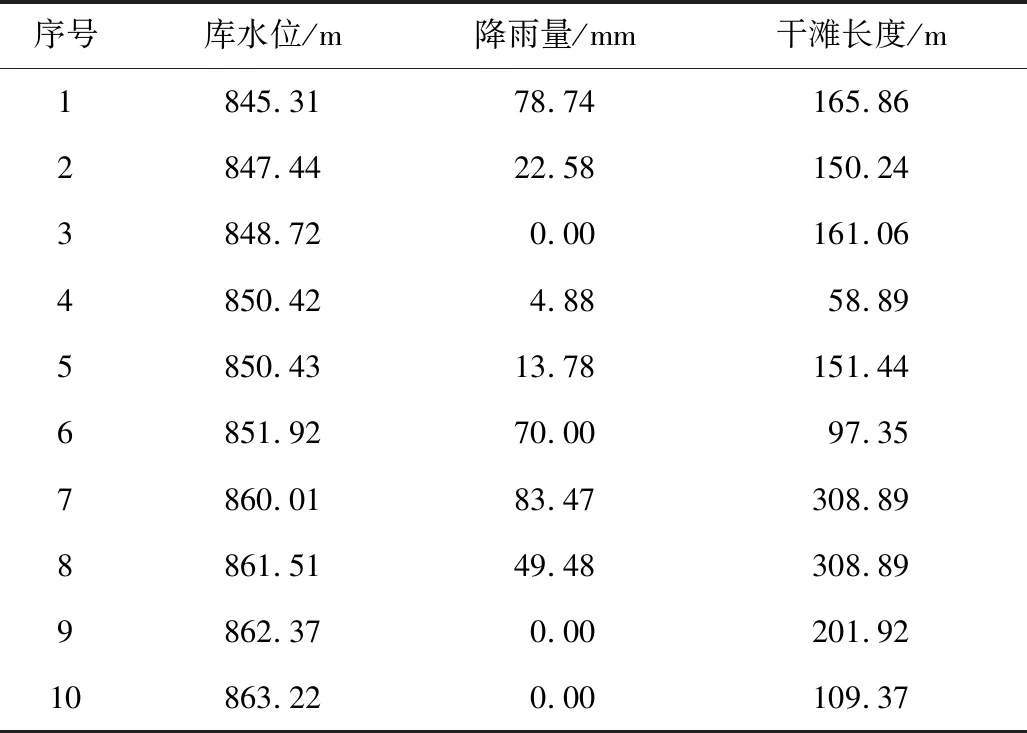
表1 Fundão坝部分历史数据Table 1 Partial historical datas of the Fundão

2 基于BP神经网络预测模型

人工神经网络技术是对大脑功能的模拟、抽象和简化，具有学习、联想和记忆功能，以及高度的非线性预测能力[14]。本文采用基于Levenberg-Marquardt算法的BP双隐层神经网络对巴西Fundão坝的排水数据进行预测建模。该双隐层网络包含1个输入层，1个输出层，2个隐藏层。其中输入层有3个神经元节点，输出层包含1个神经元节点。为了全面分析巴西Fundão坝的排水流量规律，本文提取了2011年7月至2015年3月的库水位、降雨量和干滩长度数据做训练集的输入，而对应的排水流量则为输出特征。在BP神经网络模型中，回归系数R用于评估模型的有效性，R越接近1，模型的预测能力越精准。

2.1 Levenberg-Marquardt算法

Levenberg-Marquardt算法结合了高斯牛顿法和梯度下降法的优点，是目前使用广泛的优化算法。设x(i)为当前状态的权重向量，x(i+1)为BP神经网络中更新后的权重向量，Δx为权重更新值，有：

x(i+1)=x(i)+Δx

(1)

Δx=-[2E(x)]-1E(x)

(2)

(3)

式中：E(x)为损失函数，选用均方误差；ei为排水数据真实值与预测值之差；2E(x)为损失函数的Hessian矩阵，即JT(x)J(x)；E(x)为其梯度；N为样本个数。这时对于BP神经网络：

x(i+1)=x(i)-[JT(xi)J(xi)+μiI]-1JT(xi)ei

(4)

即

Δx=-[JT(xi)J(xi)+μiI]-1JT(xi)ei

(5)

式中：μ为大于0的比例系数；I为单位矩阵；J(x)为损失函数E(x)的雅可比矩阵，即误差向量与更新权重向量的一阶微分矩阵。

此时的Levenberg-Marquardt算法由μ来控制，μ越大，越接近梯度下降法，当μ=0时，Levenberg-Marquardt变为高斯牛顿法。

2.2 神经网络结构和模型训练

多层前向神经网络具有理论上可逼近任意非线性连续映射的能力，因而非常适合于非线性系统的建模及控制[15]。根据专家小组提供的数据和Fundão大坝排洪隧洞遭到破坏的实际情况，影响尾矿排水能力的应变因素主要包括库水位(Res)、降雨量(Rai)和干滩长度(Bre)3个因素[13]。将这3个因素作为BP网络的输入层神经元，排水数据flow作为输出层的神经元。而隐含层神经元个数则根据式(6)初步确定[16]：

(6)

式中：m为隐含层节点数；n为输入层节点数；l为输出层节点数；α为1～10之间的常数。网络的初步结构设定为3-3-3-1。

网络隐含层的传递函数选用双曲正切S型传递函数tansig，输出层则使用线性传递函数 purelin。模型的训练选用trainlm，即Levenberg-Marquardt优化算法。凭此设置，使用MATLAB工具建立BP神经网络模型，经

过多次调整确定网络结构为3-4-4-1，网络结构如图1。此时的回归系数是0.985 6，说明网络的训练效果良好，训练效果如图2。其中，最大迭代次数为5 000次，网络的学习率为0.01，目标误差为0.65×10-3。

图1 BP双隐层神经网络结构Fig.1 Structure of BP double hidden layer neural network

图2 BP神经网络训练效果Fig.2 BP neural network training effect

2.3 模型预测效果验证

为了验证模型的效果好坏，取10组训练样本之外的数据即2015年3月-11月的数据输入模型中进行预测，其中，只保留库水位、降雨量和干滩长度。预测的结果与实际真值对比如图3、表2所示。

图3 BP神经网络预测结果Fig.3 BP neural network prediction results

序号日期库水位/m降雨量/mm干滩长度/m样本真值/(L·s-1)样本预测值/(L·s-1)相对误差/%12015-3-1884.988.66209.1370.5169.131.9622015-4-1885.4033.82194.7170.5169.151.9332015-5-1886.9011.67197.1164.6066.162.4142015-6-1887.542.82290.8656.2857.672.4752015-6-5887.9713.17304.0861.7559.653.4062015-6-10888.180.00295.8759.7857.184.3572015-7-1889.462.86168.2665.4764.681.2182015-9-1890.952.90290.8657.8156.622.0792015-10-1891.590.00216.3570.9569.192.48102015-11-1892.8716.26240.3869.8569.081.10

由图3可知，神经网络的预测结果与实际结果之间相差不大，变换趋势基本相同，表示该模型训练成功。由表2可知，排水数据flow(L/s)对应的10组验证数据的相对误差范围在1.10%至4.35%之间，该BP神经网络的运行时间为8 s。可见，BP神经网络预测模型的误差范围相对较小，准确度较高。

3 基于SVR算法的回归预测模型

3.1 SVR回归预测模型的建立

SVR回归即找到1个高维的回归平面，让数据集内的所有样本到该平面距离最近。SVR也是小样本数据集下性能可观的预测模型。

已知数据样本是三维向量，训练集可表示为{(xi,yi),…,(xk,yk)}，其中xi∈R3是输入变量即库水位、降雨量和干滩长度，yi∈R是排水数据实际值，i=1,2,…,k是训练样本的个数。此时构建回归超平面：

f(x)=ω·x+b

(7)

式中：f(x)为排水数据的预测值；ω为权值向量，ω·x做内积运算；b为偏移值。

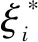
(8)

式中：ε为损失界限，控制了模型对数据的误差宽度。引入拉格朗日(Lagrange)乘子a,a*将凸二次优化问题转变为对偶问题：

(9)

求解参数，符合决策变量的数据成为支持向量回归，此时的目标函数为：

(10)

因为输入特征与输出特征属于非线性关系，本模型采用径向基核函数，函数如式(11)：

(11)

式中：y为核函数中心；σ为核函数的宽度参数， 控制了函数的径向作用范围；x为样本点。高斯核函数将数据从其特征空间映射到无穷维空间，解决了非线性不可分的问题，拟合出1条高维的曲线达到预测效果[18]。最后模型的目标函数为：

(12)

模拟过程如图4所示。

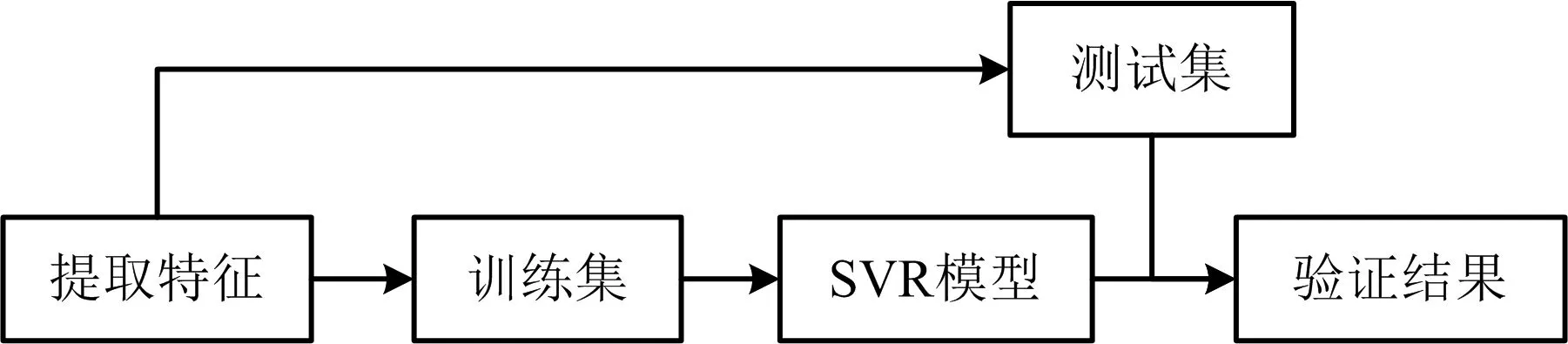
图4 SVR预测模型流程Fig.4 SVR prediction model flow chart

1)回归预测模型是基于特征属性搭建的，将2011年7月至2015年3月Fundão尾矿大坝的库水位(Res)、降雨量(Rai)和干滩长度(Bre)作为特征输入，排水数据作为输出。

2)采用和BP神经网络预测排水数据一样的测试集。调用sklearn中的svm库，核函数设置为rbf径向基函数，拟合SVR回归曲线，采用试凑法经过多次试验找到最优参数确定为gamma=26,C=1。

3)完成模型回归，得到预测结果，与真值对比计算误差。

3.2 结果验证

借助Anaconda+Pycharm集成开发环境，调用sklearn库中的svm模块，对数据集进行支持向量回归预测。目前，常用的最优参数选取方法有K折交叉验证法、留一法和试凑法。留一法和交叉验证法不能固定训练样本，无法与BP神经网络方法做结果对比，因此选用试凑法。试凑法的基本原理为：首先为函数固有的参数赋初始值，然后开始实验测试，根据测试精度重复调整参数值，直至得到满意的测试精度为止[19]。选取默认参数gamma=1，C=1，固定gamma选用不同C值确定最低均方根误差(Root Mean Squard Error, RMSE)，此时gamma=1，C=5，RMSE=3.61。再固定C值，选用不同gamma确定最低RMSE值，此时gamma=25，C=5，RMSE=2.76。重复上述步骤直至RMSE值不再降低。经过多次调试，最优参数设置为gamma=26,C=1，此时RMSE=2.74。调试过程见图5。表3为SVR模型预测结果，可知，预测排水数据相对误差范围在1.64%～9.21%之间，最大误差小于10%，运行时间为0.08 s，所以认为该模型的预测效果良好。

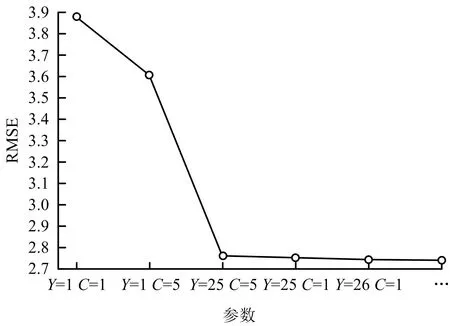
图5 SVR模型参数调试Fig.5 SVR model parameter modulation

序号日期样本真值/(L·s-1)样本预测值/(L·s-1)相对误差/%12015-3-170.5171.671.6522015-4-170.5171.681.6532015-5-164.6067.405.0142015-6-156.2859.535.7852015-6-561.7562.921.8862015-6-1059.7865.299.2172015-7-165.4761.496.0882015-9-157.8158.972.0192015-10-170.9572.121.64102015-11-169.8571.011.67

综合对比BP神经网络与SVR回归预测模型，二者的预测机制不同，预测效果也不一样。前者通过反向传播误差更新权值来预测数据，后者通过在高维空间拟合超平面使样本点距离平面最近预测数据。2个模型对比结果如表4所示，SVR回归预测模型的平均相对误差为3.66%，而BP神经网络模型的平均相对误差则只有2.34%。从时间上看，SVR预测模型要更快。

表4 模型对比结果Table 4 Results of model comparison

4 结论

1)以库水位、降雨量和干滩长度为输入，运用BP神经网络预测模型和SVR回归预测模型2种方法预测排水数据，2种模型的最大误差分别为4.35%和9.21%，均小于10%，说明模型的建立和预测结果是可行的。

2)BP神经网络和SVR预测模型克服了排水数据复杂且非线性的特点。前者的预测精度高，平均误差为2.34%，后者的运行速度快，运行时间为0.08 s。其中，核函数为径向基函数，参数gamma=26，C=1时，SVR模型预测结果最优。

3)借助BP神经网络预测模型和SVR回归预测模型，矿山安全管理部门可根据模型预测结果预测排水数据，对于尾矿库安全管理具有一定参考价值。