基于L0梯度最小化滤波和对比度受限直方图均衡的色调映射算法

段瑞，郭铖

(中国传媒大学 信息工程学院，北京 100024)

1 引言

高动态范围图像和普通数字图像相比，是一种能完整记录场景光照数据的新兴图像解决方案，它可以展现出和真实场景相同的视觉感官。真实场景中光照的动态范围可以达到，而普通的显示设备的动态范围只有102，由于在动态范围方面的巨大差距，高动态范围图像无法直接在显示设备上输出。色调映射算法通过将高动态范围图像映射为一张和真实场景具有相同感官的普通图像，进而解决了高动态范围引发的矛盾。

近年来随着高动态范围图像的普及，色调映射算法已经成为学界研究的热点。Reinhard[1]等人首先提出了一种基于摄影理论中遮光-曝光思想的色调映射方法。Reinhard首先通过全局平均亮度将整幅图像压缩到一个较小的范围中，然后利用两个不同高斯核函数对图像块分别做卷积运算的差值等操作进而形成中心-环绕函数，最后用该估值结合前面的全局压缩进行色调映射。Durand[2]等人首先提出了一种基于保边滤波分层处理的色调映射算法。该方法的贡献在于使用双边滤波将图像分为基础层和细节层，双边滤波一种既可以保留图像物体边缘又可以模糊物体内部的滤波方法，动态范围的压缩仅对基础层进行。Ji[3]等人提出了一种基于K均值聚类和自适应gamma值的色调映射算法。该方法首先对输入图像进行全局压缩，然后用双边滤波的对图像进行分层，得到的结果作为k均值聚类的输入，由此将图像分割为若干个区域。计算每个聚类簇中心可得到该类的gamma值，最终由全局压缩后的图像和gamma值决定最终色调映射的结果图像。Li[4]等人提出了一种基于视觉显著性的色调映射算法。该算法将显著性加权和边缘加权加入到导引滤波之中，利用导引滤波将输入图像分为基本层和细节层，而显著性加权用来进行全局色调压缩。

本文提出了一种基于L0梯度最小化滤波和对比度受限直方图均衡的色调映射算法。由于运用高斯核函数的图像分层很容易造成光晕现象，本文使用L0梯度最小化滤波抑制了光晕现象的发生；而经过压缩之后的图像往往对比度较弱，本文提出了基于比例分配的对比度受限直方图均衡，结果图像的对比度得到了显著提升。

2 本文算法

本文沿用Retinex算法的思想，将图像分为基础层和细节层来处理，但Retinex算法使用的高斯滤波在运算过程中会造成梯度弥散，从而在最终的效果中会产生光晕现象，所以本文使用L0梯度最小化滤波代替了高斯滤波；而单纯地经过全局压缩后，恢复图像的对比度提升不足，最终图像细节部分不突出，本文经过研究使用基于比例分配的对比度受限直方图均衡解决了这一问题。本文所提出的色调映射算法流程图如图1所示。首先利用Reinhard全局压缩将高动态范围数据归化到一个合理的区间，然后利用L0梯度最小化滤波将图像分为基础层和细节层，针对全局压缩后对比度较弱的问题，对基础层进行基于比例的对比度受限直方图均衡，然后合并细节层和基础层，利用原有的图像颜色信息进行Gamma校正。

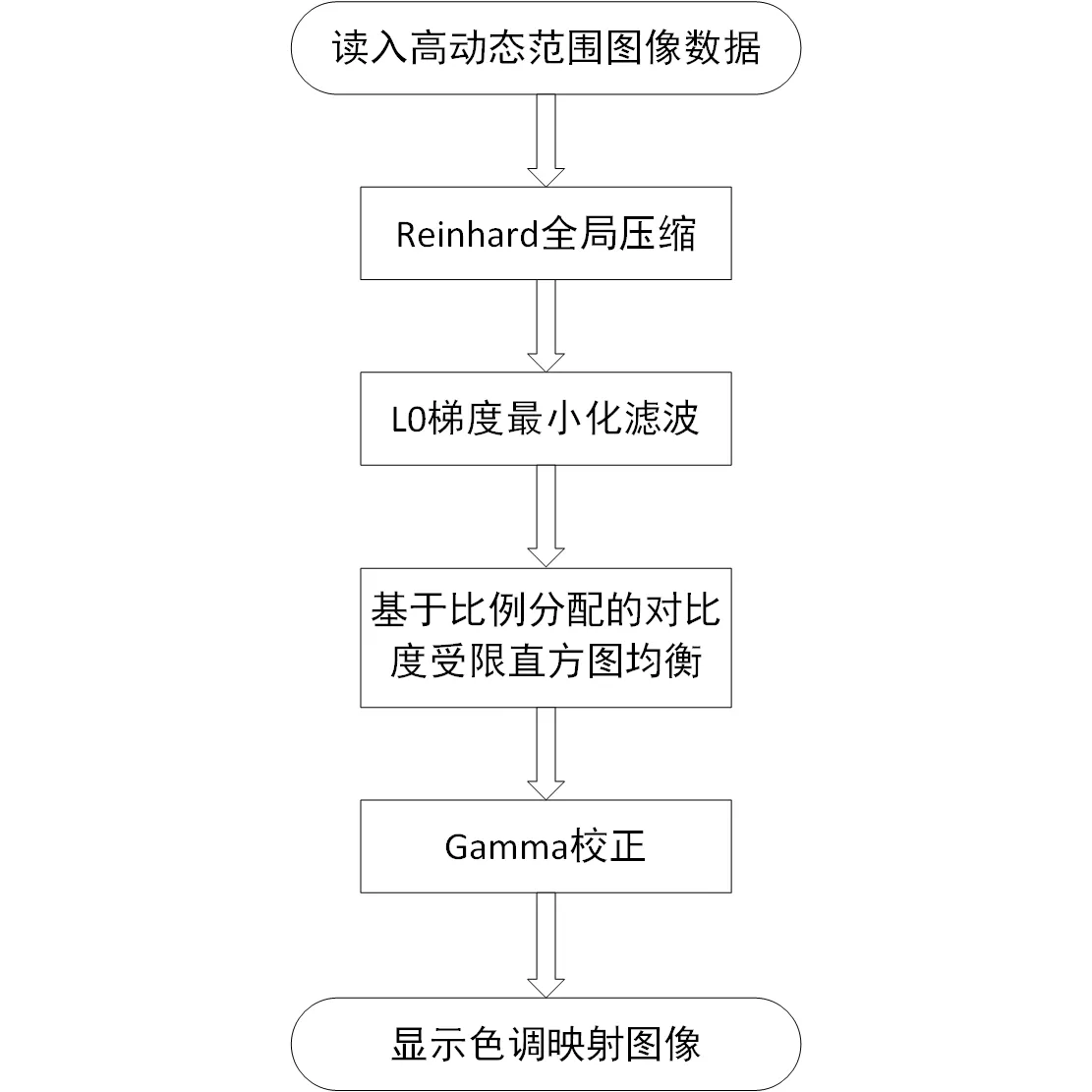
图1 本文算法流程图

2.1 Reinhard全局压缩

读入高动态范围图像后，首先进行全局压缩。Reinhard全局压缩是在色调映射算法中经常被用到的一种大幅度压缩方法。该方法首先计算整幅图像的平均对数亮度：

(1)

其中，N为图像中像素值的个数，Lw(x，y)是像素点的亮度值，δ是一个很小的修正值，作用是避免纯黑像素点对运算的影响。

那么可以利用平均对数亮度对全部像素点进行缩放，可得式如下：

(2)

其中，L(x，y)为经过缩放后的像素值，α为一个比例调整系数。

然后通过引入Lwhite就可以将像素值控制在可以显示的动态范围之中：

(3)

其中，Lwhite代表能被映射到白色的最小亮度值

2.2 L0梯度最小化滤波分层

在获得了全局压缩后的亮度后La(x，y)，考虑将图像数据进行分层处理。

基于中心环绕方程的Retinex理论认为，物体在人眼中形成的视觉感官由两部分构成，数学模型如下：

S(x，y)=R(x，y)*L(x，y)

(4)

其中，S表示人眼最终形成的视觉映像，R表示由物体本身决定的反射性质，L表示入射光因素。

并且Retinex理论指出，图像的动态范围主要是由入射光因素造成的，所以如果能够准确的分离出入射光因素，那么就能大尺度地压缩图像的动态范围。Retinex理论中，入射光形成的大尺度的低频信息，可以把这一部分称为图像的基础层；而物体本身性质决定的细节纹理等高频信息，可以把这一部分称为细节层。

对式4取对数并移项得：

logR(x，y)=logS(x，y)-logL(x，y)

(5)

而入射光因素可以用一个卷积核和原图的卷积近似表示，上可以改写为：

logR(x，y)=logS(x，y)- log(S(x，y)⊗F(X，Y))

(6)

上式的本质就是通过一个卷积核将图像亮度分为由入射光因素形成的基础层和由物体本身性质形成的细节层。

而卷积核的选取就决定了分层的是否准确和合理。最初学界提出了使用高斯滤波作为卷积核进行分层，随后发现由于高斯函数的模糊效应使得图像边缘被模糊，经过色调映射后会出现光晕现象。本文在前人的基础上，使用L0梯度最小化滤波作为卷积核，有效地解决了光晕现象的问题。

Xu[5]等人在2011年提出了L0梯度最小化滤波。L0梯度最小化滤波受到加权最小二乘滤波的启发，通过全局控制非0梯度的数量来保留物体的边缘，并平滑物体的内部。

设I为输入的原图像，S为所求的输出图像，则某个像素点p的梯度可以表示为：

▽Sp=(∂xSp，∂ySp)T

(7)

那么所求图像中梯度不为0的像素的个数可以表示为：

C(S)=#{P|∂xSp|+|∂ySp|≢0}

(8)

式8表明，只要点p在垂直或者水平方向有一个梯度不为0，则认为其梯度不为0。

最后用最小均方差的最优化框架表示所求问题：

(9)

其中，I为输入的原图像，S为所求的输出图像，第一项保证了图像结构的整体相似性，第二项保证了图像整体的平滑性。λ为平衡结构项和平滑项的比例系数，λ越大则输出图像越平滑，否则图像越尖锐。L0梯度最小化滤波利用两者之间的矛盾通过最小化均方差实现了保留边缘平滑内部的效果。

利用L0梯度最小化滤波就可以将Ld(x，y)分为细节层DL和基础层BL。

2.3 基于比例分配的对比度受限直方图均衡化

得到了图像的基础层BL之后，由于之前的全局压缩导致图像的局部对比度减弱，所以需要提升图像的局部对比度以符合人眼的感官效果。

对比度受限的直方图均衡化算法是很经典的提升对比度算法。Zuiderveld[6]等人认识到图像均衡化存在的问题在于图像直方图中尖峰的处理，那么如果用某种方法限制图像直方图中的尖峰，就可以避免直方图均衡中出现的问题。由数学推导可以知道，图像的局部对比度直接与图像直方图的尖峰正相关，所以对比度受限的直方图均衡化算法就被构造出来。

受到自适应直方图算法的启发，对比度受限直方图算法将图像划分成大小相同互不重叠的矩阵块，对每个块做对比度受限直方图均衡。对比度受限直方图均衡与传统直方图均衡的最大区别在于其设定了一个灰度值出现频率的阈值，当某个灰度值像素点出现的频率超过阈值时，就将超过阈值的部分裁剪下来分配给所有灰度值，然后再用像素值所处矩阵块的邻域矩阵块进行像素插值进而完成最终的图像变换，实现图像对比度的提升。

对比度受限的直方图均衡算法具体做法如下：

1)首先，将图像分成若干个大小相同且互不重叠的矩形块，每个矩形块内的像素数为M。

2)对每个子块计算其直方图，用h(k)表示，k为此子块中存在的灰度级数，L代表总的灰度数。

3.裁剪阈值用如下公式确定：

(10)

其中，ClipLimit时最终裁剪的阈值，normClipLimit则是裁剪参数，它决定了裁剪的阈值。直方图裁剪过程示意图如下图2：

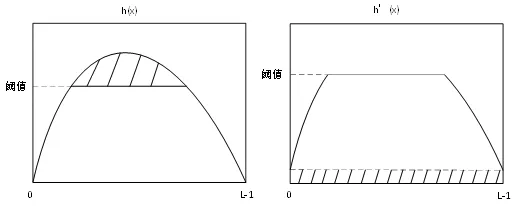
图2 对比度受限直方图均衡的裁剪过程示意图

4.将裁剪下来的像素点重新分配到每个灰度值中，分配方法采用平均分配。使用公式表达为：

(11)

avgBincr=totalE/L

(12)

其中，totalE是直方图中所有超过阈值的像素数，avgBlncr是平均分到每个灰度级的像素数。

5.再对分配过的直方图进行直方图均衡。

有时，经过一次经过裁剪和均衡形成的直方图中的某部分又超过了阈值，所以往往需要迭代地进行(4)和(5)这两步，直至没有超过阈值的灰度级数。

到底为止，每个子块都进行了对比度受限的直方图均衡算法，局部对比度都受到了限制，但直接将其作为结果会发现，因为分块的原因，使得图像的块效应严重，所以引入了后面的块插值部分。

6.由于需要消除分块造成的块边界效应，所以使用基于邻域块中心像素的插值算法来计算非块中心的像素点的最终值。

在原始的对比度受限的直方图算法中，直方图中超阈值的像素被剪切并平均的分给每一个灰度值，但经过实验发现，如果分配给较暗和较亮的区域会出现一些噪声或者过曝过暗的现象，为了消除这些噪声，此本文提出一种基于比例分配的对比度受限直方图均衡化算法。

设图像块内的灰度值概率密度函数为：

p(k)=nk/n，k0，1，，N-1

(13)

其中，n代表图像中总像素的个数，nk是所有灰度值为k的像素点数量。

定义一个参数∝，0<∝<0.5，设某灰度值imin和某灰度值imax，则∝和imin、∝和imax分别满足如下关系：

(14)

(15)

上式表明存在一个参数∝，灰度值在[0，imin]范围内的像素点的累计概率密度为∝，灰度值在[imax+1，255]范围内的像素点的累计概率密度为∝。∝值可以根据3σ准则设定：

(16)

其中，μ为子块图像像素的平均亮度，σ子块图像像素的标准差。

当子块的直方图中存在超过阈值的像素时，裁剪下来的像素不再按照均分的方式分配给各个灰度值，而是将图像灰度值分为两部分，即灰度值为[imin，imax]和灰度值为[0，imin)∪(imax，255]，两部分分到的像素数按照以下规则：

avgBlncr(i)=

(17)

式(17)表明，被裁剪的像素不再均匀的分配给每个灰度级，而是将灰度级按照分为两部分，按照这两部分的比例分配所能增加的像素数，在两部分内部再按平均原则进行分配。

将基于比例分配的对比度受限直方图均衡化作用于基础层BL，得到新的基础层数据nBL，再将nBL和细节层DL结合，即可得到初步的图像亮度数据Lnew。

2.4 Gamma校正

由于色调映射算法是对亮度数据进行运算的，所以为了保留原来的颜色信息，并且使图像更加符合人眼的视觉特性，引入基于颜色信息的Gamma校正。

首先在读入高动态范围图像时，计算像素数据各颜色通道所占比例：

Y=0.299*R+0.587*G+0.144*B+10-6

(18)

(19)

其中，10-6是为了防止纯黑点的亮度值作为分母。

最终图像各颜色通道的数值由Lnew和各原通道比例共同运算得到。定义饱和度值为s，Gamma校正值，最终可得RGB的结果为：

Rnew=((CR)S*Lnew)γGnew=((CG)S*Lnew)γBnew=((CB)S*Lnew)γ

(20)

由此就得到了最终的色调映射图像。

3 实验及结果分析

图像质量评价主要分为主观质量评价和客观质量评价。主观质量评价是通过人眼对图像的适应度和满意度来衡量结果的优劣，而客观质量评价是通过对图像某些特征的量化，通过合理的数学模型，将图像质量分数化。由于不同的色调映射算法产生的结果不同，本文通过主观评价和客观评价两种评价方法来衡量本文提出的色调映射算法，参照对象选用了5种经典的色调映射算法，以证明所提色调映射算法的有效性。

本文选用三张不同的高动态范围图像，分别使用5种经典算法和本文所提算法进行色调映射，逐一分析所得结果。

3.1 主观实验结果分析

本次采用三幅不同的高动态范围图像，运用不同的色调映射算法分别得到如图3、图4两组结果：

(a)图为本文所提算法结果 (b)图为Mantink算法结果 (c)图为Durand算法结果

(d)图为Reinhard算法结果 (e)图为Drago算法结果 (f)图为iCAM06算法结果图3 desk不同色调映射结果

如图3所示，Mantiuk算法在亮区的对比度较弱且明暗层次较少；Durand算法在暗区的层次则不够丰富，桌椅的细节都没有体现出来；Reinhard算法无大范围抑制高亮的缺点暴露出来，整幅图像出现过曝现象；Drago算法对于颜色的恢复则较弱，饱和度不足；iCAM06对于本图则抑制过度，导致整幅图像的偏灰。本算法层次性较好，对比度明显，在高亮区域的表现有明显的优势。

如图4所示，Mantiuk算法虽然保留了细节信息，但导致整幅图像的亮度过低；Reinhard算法、Drago算法和Durand算法在高亮区域的细节丢失；iCAM06算法保留颜色信息的能力较突出且层次丰富；本算法的优势在于保留了原图像中的彩色信息，但局部噪声也被放大了。

(a) (b) (c)

(d) (e) (f)图4 okas不同色调映射结果

3.2 客观实验结果分析

由于不同的色调映射算法作用同一副高动态范围图像会得到不同的结果图像，但某些结果图像之间的差别人眼是几乎无法判别的，此外还存在个人喜好因素的影响，所以没有适当的色调映射客观质量评价标准，是无法对色调映射算法做出比较的，进而无法指明色调映射算法下一步的改进方向。

TMQI指数[7]是目前学界用来评价色调映射算法的主流客观评价标准。TMQI指数主要从两个方面来衡量色调算法的优劣：1.人类视觉系统对图像的结构性信息具有选择倾向性，也就是说结构性信息更能给人留下深刻的印象，所以结构保真度是质量评价的重要参数。2.图像的自然属性，即是否与人眼观测的真实场景具有相同的感受，且TMQI中将自然属性量化，加入到最终的质量评价当中。

对上述三组图像结果求TMQI得表1。

由表1可知，本文所提算法在客观质量方面也优于一些经典算法，具备一定的有效性。本算法的优点在于对局部对比度的增强并且能恢复原图中的色彩信息。

表1 色调映射图像TMQI

4 结论

本文提出了一种基于梯度最小化滤波和对比度受限直方图均衡的色调映射算法。其中通过梯度最小化滤波进行了图像分层，抑制了光晕现象的发生，并且起到了图像增强的作用；使用了基于比例分配的对比度受限直方图均衡来提升全局压缩后的对比度，同时又引入了颜色比例信息来保证图像色偏现象的发生，在主客观实验中都有较好的表现。