极区惯导编排中地球近似模型的适用性分析

林秀秀，卞鸿巍，马 恒，王荣颖

海军工程大学电气工程学院，湖北 武汉 430033

地球的真实形状是一个不规则的球体[1-2]，所以地球的数学模型可分为第一近似模型和第二近似模型。其中第一近似为球体模型，其数学表达式简单，几何误差一般不可忽略，在中低纬度地区多应用于复杂的误差分析。地球的第二近似为椭球模型，参考旋转椭球体更接近地球的真实形状，几何误差可以忽略不计，在中低纬度地区多应用于惯导解算。在极区，地球球体模型的几何误差减小，地球椭球模型的惯导解算复杂度增加，而且由于基于椭球模型的横向坐标系横向经纬线不正交的问题引入了编排原理性误差[3-5]，球体模型也被应用于极区惯导解算[6]中。在极区导航算法的进一步研究中，球体模型由于表达式简单得到了更广泛的研究。文献[7]研究了基于球体模型的极区组合导航算法；文献[8—10]分别提出基于球体模型的极区对准方法；文献[11]研究了基于球体模型的中低纬度对极区导航模拟方法。针对具体极区导航应用中选用的地球近似模型类型一直没有明确的界定。惯导极区编排地球近似模型适用性研究对极区导航针对性研究具有重要意义。

为了实现地球近似模型的适用性分析，首先定义适用于极区的第一近似模型和第二近似模型，然后通过误差分析方法，对球近似模型的几何误差进行惯导误差分析，明确球体模型几何误差对惯导编排的影响形式，最后通过仿真对比地球近似模型的惯导误差。仿真结果表明，球近似模型几何误差会随惯导运行时间发散，而椭球近似模型的编排误差随时间变化不大，当惯导运行时间长则球近似模型不再适用于极区。

1 地球近似模型定义

1.1 球近似模型半径的选取

当选用球近似模型作为地球模型时，其原点必定位于地心，故地球模型半径的选取关系到模型对地球的拟合程度，直接影响地球模型的几何误差。在不同的应用领域中，地球模型半径选取形式都不同，常用的球体半径有等面积半径Ra、等体积半径Rv、椭球长半轴半径Re、椭球短半轴半径Rp等。在极区应用中，常选取切换位置椭球体曲率半径Rs[12]或椭球短半轴半径作为球体模型的半径[13]。本文通过取N个地球椭球模型上的点p0i(xi,yi)使用最小二乘法拟合出与椭球模型半径误差最小的地球模型。由于椭球表面上的点到地心的距离与所在位置的经度无关，所以本文以过本初子午线的切面为例。

椭球上点到球面距离的平方和M为

(1)

式中，R为由最小二乘法确定的球体模型半径。

最小二乘法要求椭球点到地心的距离与球半径的误差值的平方和为最小值，故存在

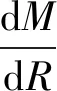
(2)

结合式(1)和式(2)求得

(3)

在极区范围的椭球弧线上分别取N=1120、N=11 112、N=111 112，得到最小二乘法拟合半径均为R=6 356.968 km，设切换位置为80°N，即取样范围为80°～90°的弧线，通过计算对球体模型半径进行对比，球体模型半径对比参数见表1。

表1球体模型半径对比参数

Tab.1Comparisonparametersoftheradiusoftheearthspheremodel

半径类型半径/km椭球上点到球面距离的平方和MN=1120N=11112N=111112等表面积半径Ra6371.010219286.842191386.1721912379.48等体积半径Rv6371.004219099.512189514.1921893660.90椭球长半轴半径Re6378.137498333.624979895.4449795513.57椭球短半轴半径Rp6356.75293.61932.859325.24切换位置椭球体曲率半径Rs6357.398246.492464.9024649.00最小二乘法拟合半径R6356.96841.48413.394132.45

椭球上的点到球面距离的平方和M的大小可以表示为球体模型与椭球体模型在忽略经纬度误差情况下的高度误差平方和。由于在惯导解算中高度误差发散，故选择的M值应尽可能小，椭球上的点到球面距离的平方和M值可以表征球体模型对椭球体模型的拟合程度，由计算结果可知，在极区范围内，与椭球体模型最相近的球体模型的半径为最小二乘法拟合半径R。

1.2 地球模型定义与对比

tan ΔL≈ΔL≈fsin 2L

(4)

由关系式可见两者最大偏差出现在纬度45°处，在极区纬度误差减小[15]，故而球体模型在一定的误差范围内可以使用。

图1 球体模型与椭球模型定义对比图Fig.1 Comparison diagram between the sphere model and ellipsoid model

2 横向坐标系惯导编排及其误差分析

2.1 横向坐标系惯导编排

横向坐标系能解决极点处计算存在奇异值的问题，在极区导航实际应用中横向坐标系的研究具有重要意义。本文使用的横向坐标系如图2所示，载体位置为横向坐标系(t系)的原点，沿参考球体模型的法线指向天为Zt轴，Xt轴沿横向纬度线指向横向正东，Yt轴沿当地横向子午线指向横向正北，Xt轴与Yt轴均与Zt轴符合右手定则。其横向经纬线如图所示，φ′为横向纬度，λ′为横向经度。

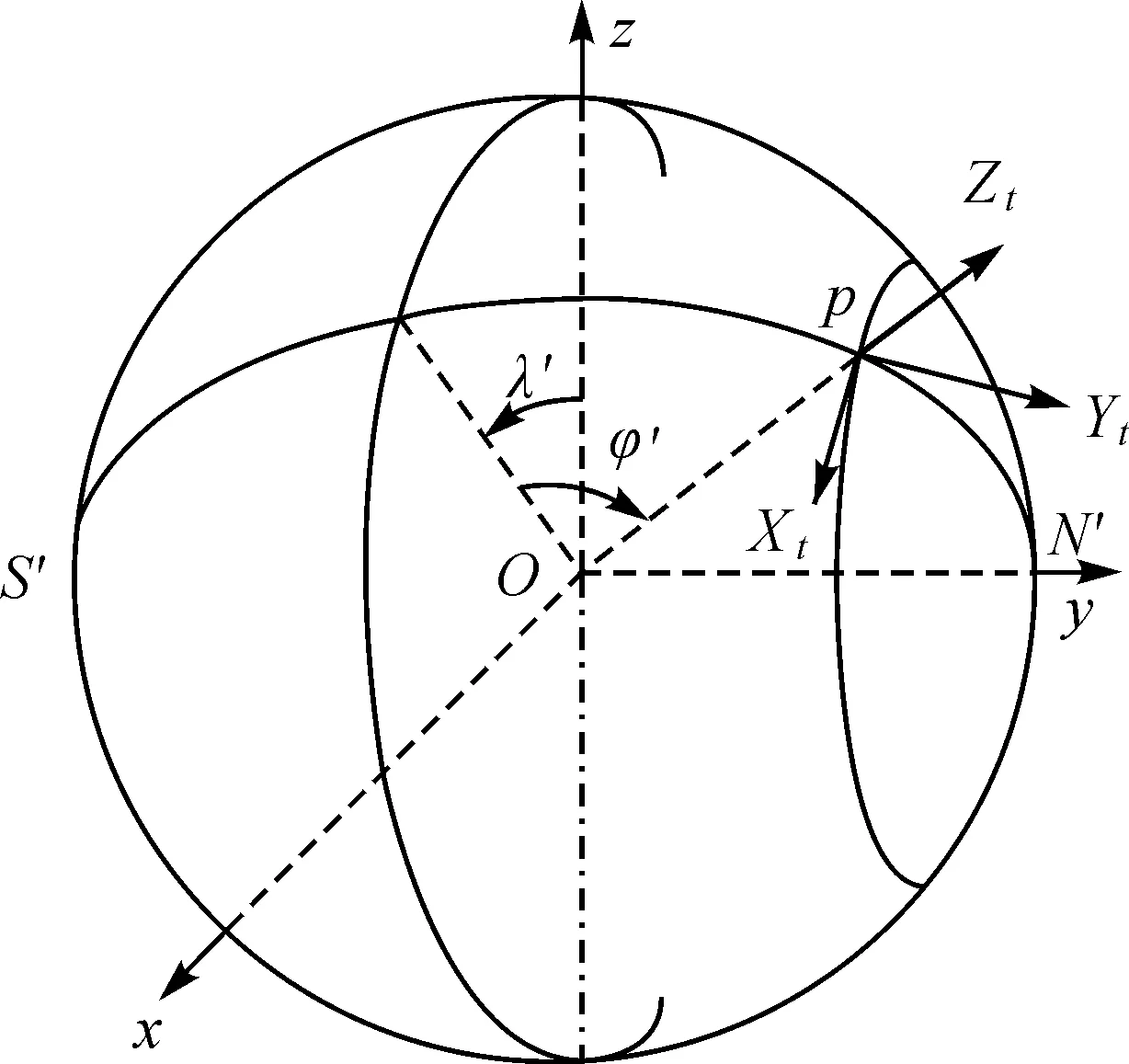
图2 横向经纬度与横向坐标系示意图Fig.2 A schematic diagram of transverse longitude and latitude and transverse coordinate system

横向坐标系的编排可分别由以下速度、姿态和位置更新方程确定(具体推导过程从略)

(5)

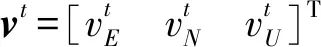
通过计算值减去真实值推导横向坐标系误差方程(具体推导过程从略)

(6)

(7)

(8)

2.2 横向坐标系误差分析

结合1.2节和2.1节可知球近似模型的几何误差会引起解算的位置误差和高度误差。在惯导解算中高度误差是发散的，且姿态误差将影响到垂线偏角误差，即球体模型的选用不仅仅会带来几何误差，还会引起惯导解算误差。本节参考文献[16]中惯导横向坐标系导航性能研究方法，推导球体模型几何误差引起惯导解算误差的具体形式，该误差分析形式与惯导解算中初始误差对惯导系统误差分析基本一致。

为了分析球体模型和椭球模型的几何误差对惯导系统的影响，在静基座条件下进行误差分析，可将误差方程写成矩阵形式

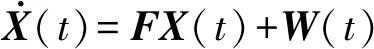
(9)

进行拉普拉斯变换得

X(s)=(sI-F)-1[X(0)+W(s)]

(10)

推导可得其特征

(11)

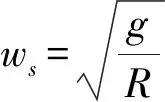
为简化计算，忽略傅科周期成分及元器件误差，推导出由几何误差引起的横向坐标系的系统误差

(12)

(13)

(14)

(15)

(16)

(17)

(18)

结合上述分析可知，球体模型的横向纬度几何误差以及姿态几何误差引起的常值误差和振荡性误差的叠加，其余项产生振荡性误差，几何误差影响随时间发散。

3 地球近似模型适用性范围分析

球体模型存在几何误差会产生惯导误差，同时在椭球体模型的编排中，为了解决横向经纬线不正交的问题，对编排作了一定的近似，带来了原理性的误差，故在地球模型和椭球体模型的选用中，要考虑两者误差的大小，将两者误差进行比较。

由于器件误差会随时间发散，为了对球体模型的惯导误差和椭球体模型的惯导误差进行对比，本文对无器件误差对球体模型误差和椭球体模型误差进行对比仿真，并通过不同时长的仿真观察球体模型误差发散对模型对比的影响。

本文以航海任务为例，对极区地球近似模型无器件误差惯导编排误差进行仿真，通过不同时长仿真结果对在航海任务中地球近似模型的使用范围进行给定，为极区模型研究提供理论依据。

3.1 无器件误差对比仿真

为了对不同地球近似模型误差仿真进行分析，假设载体初始地理位置为(80°N,125°E)，在静基座条件下，仿真周期分别为24、240、360 h。在轨迹发生器中忽略元器件带来的误差。仿真结果如图3—图5所示。

表2无器件误差不同时长地球模型编排误差对比数据

Tab.2ThecomparisondataofdifferenttimeINSarrangementerrorwithnondeviceerror

统计量24h240h360hΔδφ′/m0.033711.22.59×106Δδλ′/m0.017638.72.46×106ΔδvtE/(m/s)7.19×10-60.813.23×103ΔδvtN/(m/s)2.12×10-50.923.34×103ΔϕtE/(′)1.39×10-50.351.4×103ΔϕtN/(′)1.72×10-50.381.27×103ΔϕtU/(′)1.19×10-50.0343.48×102

对仿真结果进行分析可知，在极区无器件误差条件下：①24 h内，地球球体模型几何误差和地球椭球模型编排误差引起的惯导误差差异不大，故24 h内地球模型可以使用，极区编排选用球近似模型；②240 h后球体模型和椭球体模型引起的编排误差差异变大，两种模型差异明显，故时长超过240 h，地球模型误差较大，建议极区编排选用椭球近似模型；③在极区无器件误差条件下，地球球体模型几何误差引起的惯导编排随着时间积累，静基座条件下，360 h后球体模型的经纬度误差超过2.4×106m，速度误差超过3.2×103m/s，球体模型编排已经发散，不能使用，极区编排选用椭球近似模型。

图3 极区地球近似模型无器件误差惯导24 h编排误差对比结果Fig.3 The comparison result of 24 hours INS arrangement error of non device error with the approximate model in polar region

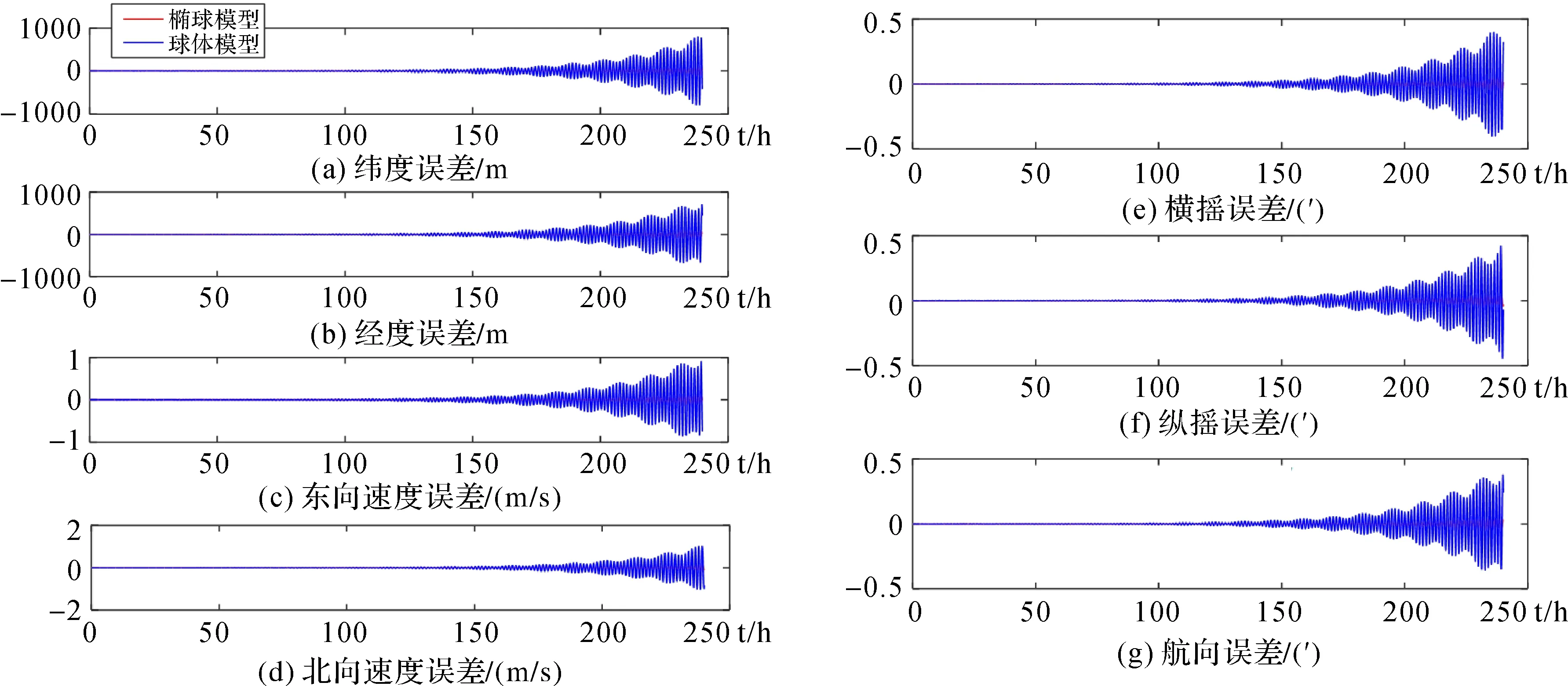
图4 极区地球近似模型无器件误差惯导240 h编排误差对比结果Fig.4 The comparison result of 240 hours INS arrangement error of non device error with the approximate model in polar region

图5 极区地球近似模型无器件误差惯导360 h编排误差对比结果Fig.5 The comparison result of 360 hours INS arrangement error of non device error with the approximate model in polar region

3.2 实际应用地球近似模型选用分析

实际极区导航应用中，元器件误差不可忽略，载体形式不同，元器件误差和惯导运行时长都不一致，本文以舰艇为例，通过对比球体模型和椭球模型横向坐标系编排误差仿真，进一步验证上一节结论，并分析极区导航应用中适用的球体模型。

由于元器件误差会使极区惯导编排发散[17]，故当航行时间达到240 h时，基于椭球模型横向坐标系编排和基于球体模型横向坐标系编排均发散，其仿真结果已经不再有效。由于极区特殊的地理环境[18-21]，组合导航[22]以及校准模式[23-25]实际应用的可行性还需要得到进一步的验证。为了验证3.1节得出的结论同样适用于存在元器件误差的实际应用，对纯惯导模式分别进行时长24 h和120 h的仿真。假设载体初始地理位置为(80°N,125°E)，地理速度为0.01 m/s，地理航向角为0°，横摇角设置为0.3°sin(πt/4)rad，纵摇角设置为0.3°sin(πt/4)rad。在轨迹发生器中将3个陀螺的常值漂移为0.001(°)/h，随机白噪声标准差为0.001(°)/h，3个加速度计零偏为10-5g，随机白噪声标准差为10-5g。仿真周期分别为24、120 h仿真结果如图6—图7所示。

图6 极区地球近似模型航海级器件误差24 h编排误差对比结果Fig.6 The comparison result of 24 hours INS arrangement error of seafaring level device error with the approximate model in polar region

图7 极区航海级器件误差地球近似模型编排误差120 h对比结果Fig.7 The comparison result of 120 hours INS arrangement error of seafaring level device error with the approximate model in polar region

分析以上仿真结果可知，航海级器件误差120 h地球模型差异大于24 h地球模型差异，与3.1节中结论一致。可以证实舰船实际航行中，运行时长超过240 h时必须选用椭球近似模型，时长少于240 h时，可选用球近似模型，以减少编排复杂度。同理，根据表3数据，飞机和导弹等短时间导航任务载体在极区可以使用球近似模型。在实际航行中，由于元器件误差的存在会使惯导系统随时间发散，一般不会存在运行时长超过240 h的无校准和组合导航的纯惯导导航模式，但元器件误差不会对几何误差引起的惯导误差产生影响，故所得结论不会因为导航模式为组合导航或校准模式而改变。

表3不同载体类型地球模型编排误差对比数据

Tab.3ThecomparisondataofINSarrangementerrorofdifferentcarriertypes

统计量导弹飞机舰船舰船5h24h24h120hΔδφ′/m0.1676.42.47348.8Δδλ′/m1.49153.62.81516.5ΔδvtE/(m/s)0.0010.080.0070.59ΔδvtN/(m/s)0.0020.043.4×10-40.42ΔϕtE/(′)9.4×10-50.065.8×10-40.39ΔϕtN/(′)8.6×10-40.053.7×10-40.19ΔϕtU/(′)8.2×10-40.010.00130.01

4 结 论

本文首先通过不同球体模型半径对比，给出极区地球近似模型的定义。在此基础上，针对球近似模型几何误差，进行横向坐标系惯导编排误差分析，明确球体模型几何误差引起的惯导误差的形式，最后通过对比球体模型几何误差引起的惯性误差仿真和椭球模型编排误差引起的惯性误差仿真差异值，对几种常见的导航载体适用的模型进行判断。得到以下结论：①在极区通过最小二乘法拟合的半径R=6 356.968 km确定的球体模型与椭球模型最相近；②球体模型的横向纬度几何误差以及姿态几何误差会引起常值误差和振荡性误差的叠加，其余几何误差项产生振荡性误差，几何误差影响会随时间发散；③在无器件误差静基座下判断出球体模型适用于时长小于240 h(10 d)的导航任务，椭球体模型适用于时长大于240 h的导航任务；④针对不同载体类型，根据其不同器件误差和不同任务时长对舰船、飞机和导弹进行分析，建议在极区舰船使用椭球模型，而飞机和导弹使用球体模型。