具有腐蚀缺陷的输气管道的可靠性分析

孙萍萍

中国石化胜利油田分公司滨南采油厂

随着国民经济的持续发展，各地的地铁系统以及高压输电系统也在不断建设，地铁和高压输电系统在运行过程中会有直流杂散电流流入、流出，当电流以金属管道作为导体形成回路时管道将面临严重的腐蚀危害。在西气东输一线、二线等大型工程中，输气管道大多采用埋地敷设的方式，由于输气管道会穿越部分一线、二线城市，不可避免地会受到杂散电流的干扰而产生腐蚀，在管道敷设以及服役过程中，会在局部产生应力集中现象，最终将会导致管道失效。近年来国内外学者通过可靠性理论对管道进行了大量的研究[1]，如帅健[2]将影响管道剩余寿命的各种因素看成是分布各异的随机变量，建立了预测管线失效的概率数学模型，并研究了腐蚀速率、缺陷深度、管道壁厚和工作压力等因素对管线可靠性的影响；张广利等[3]引入可靠性理论，利用蒙特卡洛模拟技术研究管道可靠度随缺陷尺寸变化的规律，以及通过敏感性分析，对比评价参数对管道安全可靠性的影响，并进行排序，建立含腐蚀缺陷管道评价准则的概率评价方法；AHAMMED[4]研究了含局部腐蚀管道的可靠性。

本文介绍了输气管道可靠度的计算方法，根据ASME B31G—2009给出了基于B31G的极限状态方程，采用Monte-Carlo法对目前西气东输使用最为广泛的X80管道进行了可靠度评估，最后分析了不同参数对管道可靠度影响的敏感性。

1 具有缺陷的输气管道的可靠度计算

采用B31G—2009标准对具有缺陷的管道进行可靠性分析，功能函数为

式中：Z为极限状态方程；M为Folias膨胀系数；pf为失效压力，MPa； pop为运行压力，MPa；t为管道壁厚，mm；SMSY为材料的屈服强度，MPa； D为管道外径，mm；d为腐蚀缺陷深度，mm；L为腐蚀缺陷长度，mm。

Z＞0时，管道处于安全状态；Z=0时，管道处于极限状态；Z＜0时，管道则为失效状态。

可靠性也被称之为可靠度，是指产品在规定的时间以及条件下能否完成预定功能的度量。基于可靠性的设计和评价方法的核心在于极限状态方程的计算，可以通过多种方法完成，为了回避管道可靠度分析中的数学困难，不考虑功能函数的复杂性，将采用Monte-Carlo法对管道进行可靠性分析。

由概率定义可知，某事件的概率可以用大量试验中该事件发生的频率来估算，当样本容量足够大时，可以认为该事件的发生频率即为其概率。因此，可以先对影响其可靠度的随机变量进行大量的随机抽样，然后把这些抽样值一组一组地代入功能函数式，确定结构是否失效，最后从中求得结构的失效概率。

应用Monte-Carlo法根据管道的基本参数产生1组符合随机变量分布的1个样本Xi（i=1，2，…， k），代入到极限状态方程Z=g(x1，x2，…，xk)中，可以计算出1个随机数。通过此方法反复进行n次模拟，可以得到n个随机数，最后统计出大于零的数量为m，当n→∞时，根据伯努利大数定理及正态随机变量的特性，可以得到可靠度为m/n。对于输气管道，具体的操作流程见图1，由于取值的数量较多，在Matlab程序中通过编程实现可靠度的计算，为了保证计算结果的准确性，取仿真次数n为106。

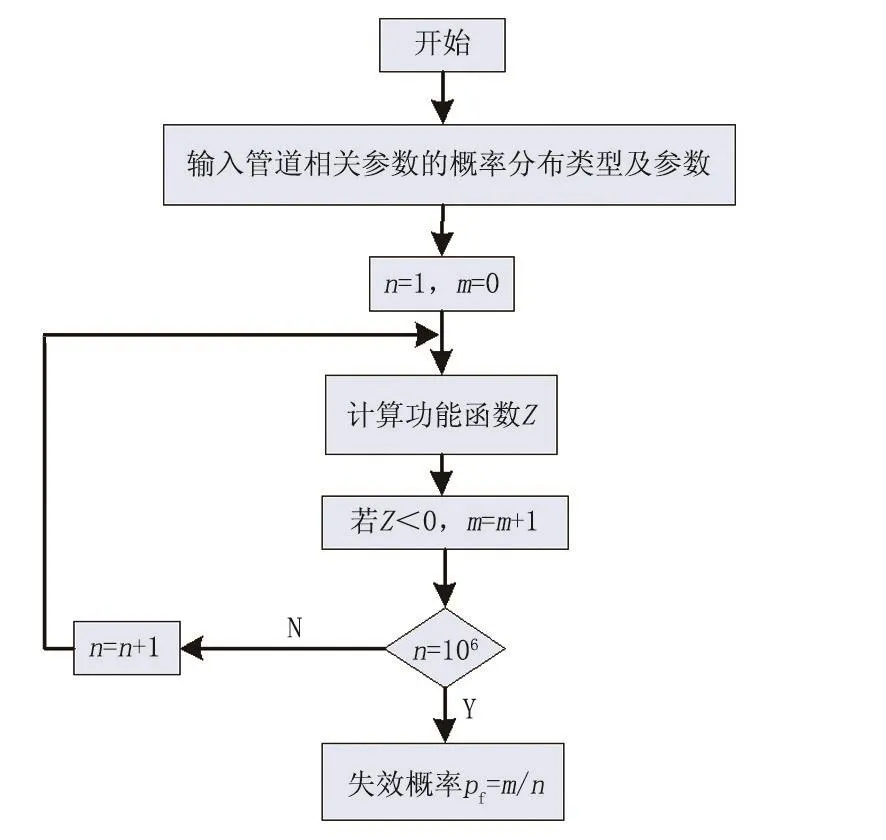
图1 Mont e-Car l o法计算流程图Fig.1 Calculation flow chart of Monte-Carlo method

2 实例计算

根据参考文献[5]，管道的基本参数如表1、表2所示。

表1 管道尺寸Tab.1 Pipe dimensions

表2 管道运行压力Tab.2 Pipeline operating pressure

2.1 目标可靠度

本文采用基于可靠性理论的分析方法来评估腐蚀管线。为此，以API 579—2007提出的管道目标可靠度为依据，其中一类地区对应低风险，二类地区对应中风险，三、四类地区对应高风险（表3）[6]。受干扰较大的管道一般处于高风险地区，所以下文取0.999 99为管道目标可靠度。

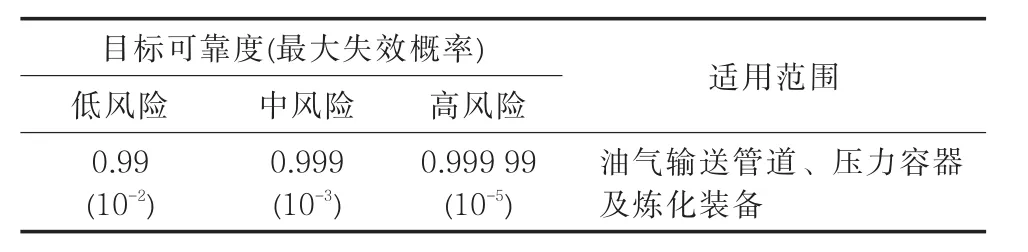
表3 目标可靠度Tab.3 Target reliability

2.2 可靠度计算

取腐蚀缺陷平均长度为管道外径的一半，变异系数为0.1；取缺陷深度分别为壁厚的10%、20%、30%、40%、50%，变异系数为0.1。采用基于B31G的Monte-Carlo法计算管径为1 219 mm的X80管道的可靠度。计算结果（表4）表明，当腐蚀深度小于管道壁厚的30%时，可靠度都远高于0.999 99，随着腐蚀深度的加深，当深度大于管道壁厚的40%时管道运行时的可靠度小于目标可靠度0.999 99。所以当腐蚀深度大于管道壁厚的40%时应当采取相应的安全措施，如更换新的输气管道或者降低当前的运行压力。

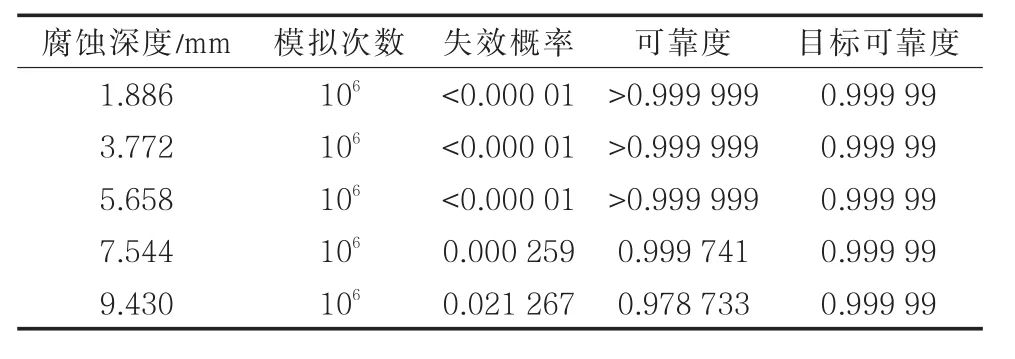
表4 可靠度计算结果Tab.4 Reliability calculation results

2.3 敏感性分析

对于有腐蚀缺陷的输气管道，管道的不确定参数包括管道外径、管道壁厚、拉伸强度和管道内压、缺陷长度和缺陷深度，分别取参数标准差的50%、100%、150%、200%、250%、300%对管道进行可靠度分析，为保证结果的精确性，每次模拟次数为106。结果如图2所示，控制各随机管道参数变异系数不变，当增大管道壁厚、拉伸强度、管道外径、管道内压、缺陷长度和缺陷深度六个参数中一个参数的变异系数之后，管道的可靠度有所降低。其中对管道可靠度影响最大的是缺陷深度，其次是管道内压和管道壁厚。

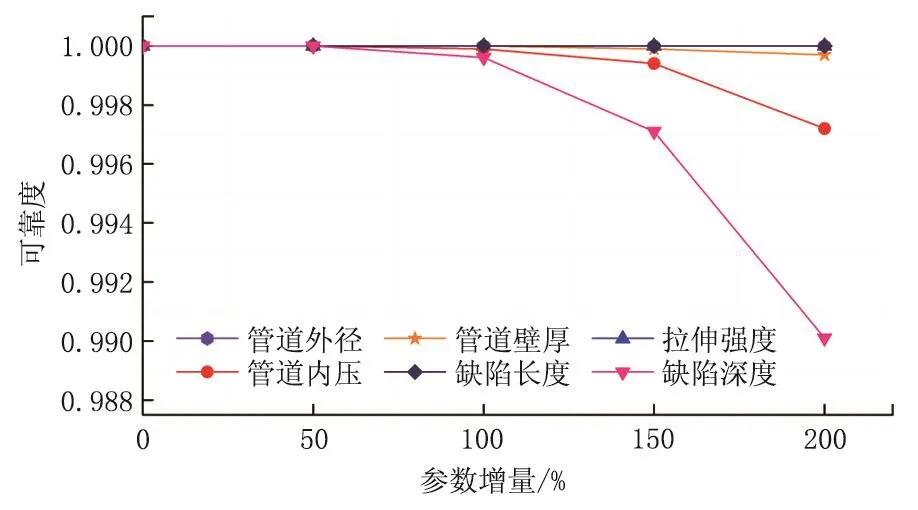
图2 参数标准差变化对可靠度的影响Fig.2 Influence of the variation of parameters standard deviation on reliability

3 结束语

地铁及高压直流输电系统在运行时会对管道产生杂散电流干扰，电流的流出端会加速管道的腐蚀。以西气东输二线所用的X80管道为算例，基于B31G标准对含有腐蚀缺陷的管道建立了可靠性模型，将各不确定的输气管道参数带入到极限状态方程中，由于计算难度较大，采用了Monte-Carlo法来获得可靠度结果。经过分析得到当腐蚀深度大于管道壁厚的40%时，管道可靠度计算结果小于目标可靠度，应采取相应的安全措施，如更换新的输气管道或者降低当前的运行压力。对各个参数进行敏感性分析表明，对管道可靠度影响最大的是缺陷深度，其次是管道内压，所以在管道运行期间应当主要关注管道的腐蚀程度以及管道压力的变化。