黄茨滑坡时间预测预报

李嘉祺 康 田 周鹏超 孙 昊

(中国地质大学(武汉)，湖北 武汉 430074)

1 概述

大量的研究与实践表明:由于滑体变形规律的复杂性，滑坡的中长期预报较难，不确定性较为显著；而在短期和临滑预报阶段，滑坡位移时序变化相对确定，此时滑坡剧滑时间预报才有实现的可能[1]。

1995年1月30日凌晨，甘肃省兰州市盐锅峡镇黄茨村北侧黑方台南缘突然发生滑坡，但由于铁科院西北分院已预报其即将于1995年1月31日～2月7日整体下滑，从而避免了大量的人员伤亡和经济财产损失[2,3]。本文以黄茨滑坡为例，采用斋藤迪孝法、曲线回归分析模型和灰色GM(1,1)模型分别对黄茨滑坡进行短期时间预测。

2 黄茨滑坡概况

黄茨滑坡位于甘肃省兰州市盐锅峡镇黄茨村北侧黑方台南缘，是一个典型的由灌溉引发的台缘滑坡，其自软塑黄土至卵石层底面为18 m为持水层，地下水渗流层面(5 cm厚的饱水软塑黏土)即为滑面位置。

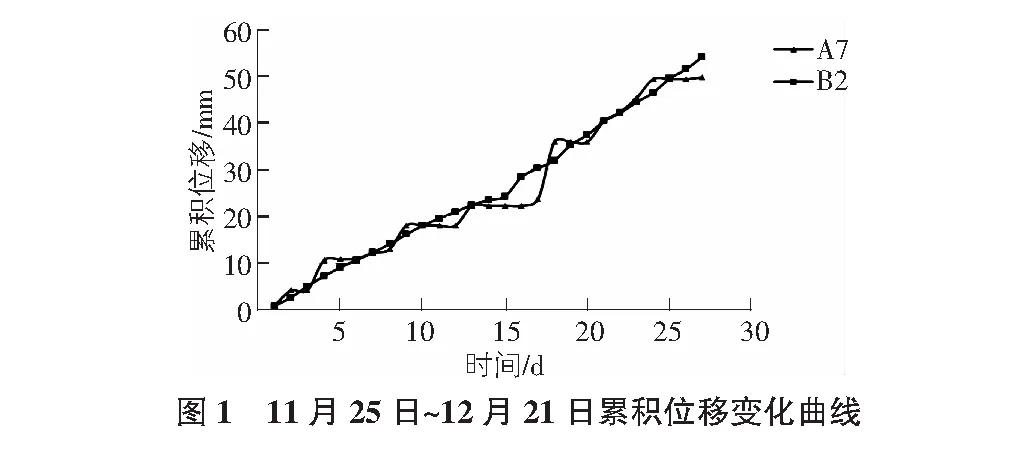
1994年8月～1995年1月，铁科院西北分院对其进行了长达半年的监测，积累了大量的监测资料，文章预测模型主要以电子自记单点位移计的数据为基础。12月22日～1月22日，仪器故障，无资料。分析A7和B2的监测数据，1995年11月25日～12月21日共27 d数据见图1，1996年1月23日～1996年1月29日数据见图2。

3 时间预测预报

3.1 Verhulst灰色模型预测

Verhulst生物生长模型最早由晏同珍教授应用于滑坡预测预报研究[4-6]，其微分方程形式是：

(1)

(2)

(3)

设位移观测数据的时间间隔为Δt，则式(3)可写成：

(4)

滑坡位移监测数据(等时间距=Δt)为：

对监测数据处理得到累加生成数列：

(5)

式(4)和(5)联立得:

(6)

(7)

a,b系数根据下式求解：

(8)

其中，矩阵(A┆B)为矩阵A和B的合矩阵。

学生自评问卷的调查结果显示，94%的学生认为知晓游泳自救与水上救助知识对学会安全游泳是非常重要的，98%的学生渴望学习游泳自救与水上救助，提升这方面能力，而57%的学生不喜欢上体育课是因为“竞技游泳技术教学为主（蛙泳、自由泳等）与我无关”。

表1 观测点A7日位移值

根据表1所列数据，采用7个点的位移观测数据，数据观测的时间间隔为1 d，t1=1995年1月23日，按照Verhulst灰色系统模型建模的步骤建立预测方程，得到：

a=0.295 563，b=0.001 774。

将a,b代入得时间预测方程为：

(9)

滑坡的预测破坏时间为1995年1月31日13点55分。

表2 观测点B2日位移值

根据表2所列数据，采用7个点的位移观测数据，数据观测的时间间隔为1 d，t1=1995年1月23日，按照Verhulst灰色系统模型建模的步骤建立预测方程，得到：

a=0.625 778，b=0.002 4。

将a,b代入得时间预测方程为：

(10)

滑坡的预测破坏时间为1995年1月30日0点18分。

3.2 GM(1，1)模型

灰色GM(1，1)模型和Verhulst模型思路上是一致的。灰色系统对于信息不完整或不完全的实际情况具有良好的适用性，它能够解决贫信息，少数据的实际问题，其中GM(1,1)模型[7-11]在滑坡预报中得到广泛的运用。其原理如下：

tr=ln(tanα)/a(X(0)(1)-b/a)/(-a)>tn。

其中，tr为滑坡监测资料最后一个数据所对应的时间。

利用11月25日～12月21日监测数据进行滑坡短期预测反分析，结果如表3所示。

表3 基于GM(1,1)模型预测结果

3.3 斋藤的蠕变模型预测

斋藤迪孝方法是以蠕变理论为依据,得出均质土滑坡时间预报的一种经验公式[11-14]，具体如下：

1)计算地面位移:

x1(t1)，x2(t2)，x3(t3)…。

2)计算平均速度的倒数:

4)画直线连接A和B。

5)延长直线，交横轴于点tr，即为滑坡破坏时间。

运用该模型对黄茨滑坡进行预报，选取23,26,29三天数据进行蠕变破坏模型计算，计算结果如图3所示。当y=0时，x分别等于32.606,38.125，即监测点A7和B2的预测时间分别为2月1日14点33分和2月7日3点00分。

3.4 小结

灰色Verhulst模型，依据1月23日～1月29日机械式位移计A7日数据的预报结果为1月31日13点55分，最接近实际时间。而斋藤的蠕变模型得出的破坏时间则分别为2月1日14点33分和1995年2月7日3点00分，不同数据预测的结果差异很大。GM(1，1)模型中进行短期预报时，1994.12.15～1994.12.21时间内电子式位移计B2监测资料预测效果比较好，而其他情况下差别比较大。

4 结语

1)三种预测模型都能大致预测出滑坡的滑动时间，其中Verhulst模型与斋藤的蠕变模型适宜于滑坡的临滑预报，GM(1，1)模型适用于中短期预测预报。

2)滑坡的时间预测精度与选取数据有关，主要包括三部分：监测数据的精度；监测孔的分布位置；滑坡运动所处的阶段。同时在预测前对监测信息数据列进行分析研究，以便获得信息序列的特性，依据得出的特性对其进行相应的预先处理。

3)对于日本斋藤的蠕变模型预测时，其t1与t2的位移s有很大的任意性，而预测精度又与t1和s的取值有很大关系，所以其预测精度与适用性有待进一步研究，其模型有待进一步完善。