基于两个相关资产的亚式期权定价研究

贾念念 谢嘉欣

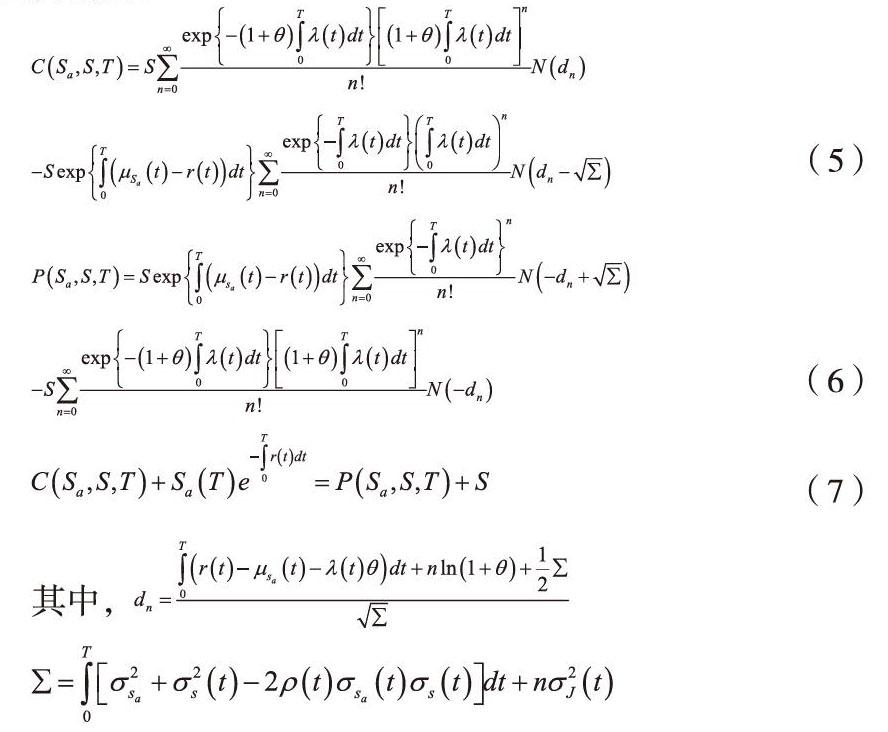
摘要：本文研究具有浮动敲定价格的亚式期权，应用物理概率测度和公平保费原理的理论，求出亚式期权的期权定价公式。假设房价波动遵循非齐次泊松跳跃扩散过程，期权敲定价格满足公式，得到亚式期权的定价公式及亚式看涨期权的平价公式。

关键词：亚式期权定价 公平保费 非齐次泊松跳跃扩散

一、问题介绍

近几十年来，金融衍生市场发展迅速，期权作为一种金融衍生产品，其定价模型依赖于原生资产价格的演化模型。随着市场需求复杂程度的提高，金融机构推出交易方式、交易价格更灵便的新型期权。本文研究的是新型期权中的一种强路径依赖期权，即亚式期权的定价问题。亚式期权已经被广泛的应用于金融市场中，但是其定价问题仍然没有得到很好的解决，主要原因是其需满足市场无套利及市场的完备性。如果市场存在套利机会或者不完备，那么亚式期权无法用传统的Black-Scholes公式进行定价。1998年Mogens Bladt和Tina Hviid Rydberg第一次提出期权的精算定价方法，在没有以上市场假设的前提下，给出了精确的欧式期权定价公式，证明了房价波动满足几何布朗运动，同时求出精算定价和Black-Scholes定价。然而由于他们没有假设市场无套利，所以其公式被广泛的应用于完备的市场，而对于无套利的不完备市场仍不可适用。

亚式期权是一种新型期权，由标准期权衍生而来，按执行价格类型可分为固定执行价格和浮动执行价格。本文只解决具有浮动执行价格的亚式期权定价问题，引入精算思想，假设房屋波动价格满足非齐次的泊松跳跃扩散过程，两资产的浮动价格遵循一个过程相关模型，得出亚式看涨期权表达式及其平价公式。

二、精算定价模型

由精算定价满足公平保费原则，多方期权、期权有效期内的短期收益将承担一些潜在风险，这些风险除了保险费外，还有期权的附加费用，我们将期权定价问题转换为期权承担的风险测度大小问题。考虑到连续时间内金融市场只有两个资产：一个是无风险资产，即在t时刻的无风险利率;另一个是风险资产，即在t时刻的资产价格，考虑到在上，是定义在完备概率空间上的一个随机过程，其中，是一个大于零的常量，在此引入精算定价的期权的概念。

假设风险资产价价格和无风险资产价格满足：

和为负常数，为收益率，为房价的波动率，为完备概率空间下的标准布朗运动。

定义1.1：假设是关于时间t的实值函数，即在t时刻的瞬时收益，则房价的期望值为

定义1.2：，分别表示到期日的看涨看跌期权价格，敲定价格K，在t=0时期权价格为：

和是A和B的指示函数，看涨-看跌期权在到期日可以实施当且仅当满足条件：

注：①定义1.2缺少金融市场对期权定价的先决条件，因此在无套利的平衡市场或是存在套利机會的不平衡市场都是有效的，然而在由预期贴现率计算潜在风险资产、无风险资产贴现到无风险利率的时候仍存在风险。

②与传统实施条件不同的是，精算模型的实施条件为。

③表示由实际概率分布得到的期权价格。

三、亚式期权模型

在金融市场中，房价波动分为两个部分：其一为普通的价格波动，由个人无意识的交易引起，对市场影响较小;其二为不寻常的价格波动，由于一些重要政策、信息的发布使得房价忽高忽低，这样的变化没有理论可以遵循，因此这样变化的房价满足非齐次泊松跳跃扩散过程，该模型在1976年由Merton提出。

具有浮动执行价格的亚式期权其最终收益依赖于某一时间段内随机波动的平均价格，但它的稳定性远远超过房价本身，并没有出现波动异常，其过程由随机过程的价格变化来描述。由于浮动执行价格变化的过程满足过程，所以综上本章中亚式期权下的两个相关资产模型服从非齐次泊松跳跃扩散模型，浮动敲定价格满足公式。

考虑到连续时间内的金融市场已经成熟，在完备的概率空间下，无风险利率为常数，房价和具有浮动敲定价格的亚式看涨期权分别满足以下微分方程：

是定义在概率空间上的二维标准布朗运动，且，，由时间确定函数可得出在此特定环境下随机微分方程的解。表示在上的跳跃次数，是非齐次泊松过程中的独立参数。表示分布随机变量，表示跳跃高度，和、相互独立且，满足标准正态分布

，表示的方差。是的无条件

期望，由泊松跳跃过程在房价中逐渐增长。

定理2.1随机微分方程（3）、（4）的解为：（证明见[3]）

定理2.2，，，对于任意实数a，b，c，d，，有以下结论：（证明见[4]）：

推论2.3表示房价中亚式期权的价格，表示波动区间内（3）、（4）的各自行使价格，亚式期权价格及平价公式分别为：

其中，

注：①当趋于0时，房价不再跳跃，推论2.3是房价波动时的价格公式。

②当连续时，服从均匀泊松跳跃过程。

③对于支付红利的亚式期权同样适用于以上公式，消去红利的贴现值即为当前房产价格。

四、结语

本文参考了[1]中的亚式期权保险精算定价模型，证明了房价的波动遵循几何布朗运动及一致连续的Black-Scholes公式。对于相应市场的亚式期权定价，假设房价遵循非齐次泊松跳跃扩散过程，浮动敲定价格满足公式，得到两种相关资产的亚式期权定价公式及平价公式。

参考文献：

[1]Bladt M，Rydberg T H. An actuarial approach to option pricing under the physical measure and without market assumptions[J]. Insurance：Mathematics and Economics. 1998.22（1）：65-73.

[2]Merton M.C. Option pricing when underlying stock returns are discontinuous[J]. Journal of Financial Economics，1976（3），125-144.

[3]Knut K，Aase. Contingent claims valuation when the security price is combination of an Ito process and a random point process[J]. Stochastic process andt heir Applications，1988.28（2）：185-220.

[4]A.Dravid，m. Richardon，and T.sun. Pricing Foreign Index Contingent Claims：An Application to Nikkei Index Warrants[J]. The Journal of Derivatives，Fall 1993，pp. 33-51.

[5]John. Hull，options futures and derivatives[M]. Zhang Tao wei，translated. Beijing：Huaxia publishing

house 1997：424-426.

[6]Jiang Li，option pricing in mathematical models and methods[M]Beijing：higher education press，2003：74-89.

[7]Yan Hai feng，Liu Sanyang，stock option pricing model with Poisson jump[J]Journal of engineering mathematics，2003（5）：35-4.