一种基于悬臂梁结构的微冲量测量方法
王大鹏,叶继飞,李南雷,王 青,王健博
(1.航天工程大学,激光推进及其应用国家重点实验室,北京 101416;2.西安卫星测控中心,陕西西安 710043)
0 引言
基于多颗微小卫星的编队、集群、星座,可承担更为复杂的空间任务[1],是未来卫星技术发展的趋势之一[2]。微推力器是微小卫星的关键部件,其推进性能直接影响航天器空间任务的完成[3]。单脉冲冲量是衡量微推力器推进性能的重要参数之一,大小通常在10-8~10-3N·s量级,需要在工程应用前对其进行精确测量。
目前测量原理基本都是基于力的动力效果,将冲量测量转换为测量台架的振动幅值或转动位移[4],典型装置有扭摆结构[5]与单摆结构[6]。无论是扭摆结构还是单摆结构,都需要将推力器与测量装置固连,属于直接测量法,存在易受介质供应管路及测控电缆影响、推力器及附件工作引入噪声等局限性[7]。尤其当推力器在研发阶段,工作附件较多,以及装星后测试时,采用扭摆及单摆结构难以进行测量[8]。然而,当采用间接测量法时,测量的是推力器喷射羽流冲击力,为非接触测量,可以避免以上问题。间接法中,悬臂梁结构简单,加工方便,测量时既作为喷射羽流的承接元件,又作为形变元件,还可根据测量需求改变尺寸以调整工作频带,已成为间接法中广泛应用的力学结构。
目前,悬臂梁已广泛应用于推力器稳态推力的测量[9-11],所依据的原理是稳态弯曲量与外力大小成线性关系。相比之下,对于冲量测量的研究相对较少,测量理论显得不足。文献[12]采用悬臂梁测量激光烧蚀推进工质产生的μN·s量级冲量,但在标定系统参数时并没有考虑悬臂梁高频振动的影响。其他领域,文献[13]介绍了悬臂梁在N·s量级脉冲电子束喷射冲量测量中的应用,也未考虑高频影响。
本文在悬臂梁动力学模型的基础上,将高频振动考虑在内,确定了测量系统传递函数。在分析系统脉冲响应特性的基础上,确定了冲量解算及参数标定方法,最后搭建了实验平台,通过实验验证了测量方法的正确性,并分析了测量误差。
1 系统传递函数的建立
单位脉冲力的Laplace变换为1,求得单位脉冲下系统响应,做Laplace变换即可求得测量系统传递函数。
1.1 悬臂梁动力学模型
悬臂梁结构模型如图1所示,截面尺寸为w×h,长度为l,密度为ρ。将阻尼视为线性阻尼,阻尼系数为c,在分布载荷f(x,t)作用下,弯曲振动方程为[14]
(1)
式中:y(x,t)为x处挠度;E为杨氏模量;I为截面二次矩,I=wh3/12;ρ1为单位长度质量。
图1 悬臂梁结构模型
根据悬臂梁边界条件,系统响应是无穷阶主振动的叠加:
(2)
式中:φi(x)、Qi(t)分别为i阶主振动的模态函数、时间函数。
i阶固有频率ωi为
(3)
式中:ωi为角频率,rad/s;ω1为振动基频;ωi(i≥2)为振动高频。
βl由频率方程cosβlchβl+1=0确定。模态函数φi(x)为
φi(x)=cosβix-chβix+ξi(sinβix-shβix)
(4)
(5)
1.2 传递函数求解
为研究方便,将喷射羽流冲击力等效为作用于lf位置处瞬时集中作用力,瞬间冲量为S,则单位长度冲量为Sδ(x-lf)。
零初始条件下,S=1时,在x=lf处取单位长度杆,根据动量增量等于外力冲量可得:
(6)
则梁的初始条件为
(7)
将初始条件带入式(2)可得:
Qi(0)=0
(8)
(9)
上式两端乘以φj(x)(j=1,2,…),并对x积分,根据悬臂梁模态正交性可得:
(10)
瞬间冲击力作用后,悬臂梁开始自由振动。令式(1)中f(x,t)=0,将式(2)带入式(1)并乘以φj(x),结合悬臂梁模态正交性可得:
(11)

(12)
将阻尼系数表示为c=2ρlζjωj,ζj为各阶振动的阻尼比。根据式(2),系统传递函数G(x,s)为
(13)
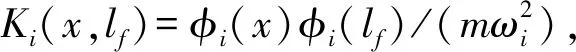
因而,悬臂梁测量系统结构上等效于无数个增益值为Ki(x,lf),固有频率为ωj,阻尼比为ζi的二阶欠阻尼子系统的并联,如图2所示。

图2 悬臂梁测量系统简化结构图
2 冲量测量方法
在分析悬臂梁脉冲响应特性的基础上,确定冲量解算及参数标定方法。
2.1 冲量解算方法
脉冲力Sδ(x-lf)作用时,R(s)=L[Sδ(x-lf)]=S,根据式(13),系统响应为
(14)
易得系统脉冲响应在时域表达式为
(15)
令y′(x,t)=0,可得第i阶响应的第j个极值点对应时间tj为
(16)
将式(16)带入式(15)中,可得第j个极值点Pj为
(17)
其中,j=1 时,即t1=φi/ωdi时,可得yi(x,t)最大值:
(18)
式(18)表明,[yi(x,t)]max值与冲量大小S为线性关系,线性系数记为Mi。
相对于基频振动,高阶振动可视为噪音干扰。测量得到y(x,t),通过低通滤波得到y1(x,t),求得[y1(x,t)]max,标定出M1大小,即可解算出S大小:
(19)
2.2 参数标定方法
式(19)中,M1为待标定参数。由于实际中很难精确产生一定大小冲量的脉冲力,M1无法直接标定,需根据其他参数标定结果间接计算M1。由式(18)可得:
(20)
可以通过标定出K1(x,lf)、ω1、ζ1,再计算得到M1。
K1(x,lf)为一阶子系统增益值,阶跃力f0δ(x-lf)作用下,一阶子系统响应及系统响应的终值分别为
(21)
推力测量中,受温度、推进剂喷射粒子等因素影响,悬臂梁性能参数可能发生变化,需要在测量中进行现场标定[15],电磁力为常用标定力形式[16],本文通过电磁力方法产生f0δ(x-lf),进行动态标定。
阶跃响应的动态分量在阻尼的作用下逐渐衰减,t=∞时,动态分量衰减至零,而稳态分量在外力作用下一直存在,最终结果与静态加载外力(加载过程极其缓慢)相同。由梁的弯曲方程,集中力载荷f0作用在lf处,x处挠度(位移)v(x)表达式为
(22)
式中k(x,lf)反映了外力与弯曲量之间的比例关系,与x处刚度系数为倒数关系。
综合式(21)、式(22)可得:
(23)
式(23)表明,系统增益值等于位移测量位置刚度系数的倒数。根据式(21)、式(23),η可表示为
(24)
η确定后,带入式(21)可得:
(25)
ω1、ζ1为一阶振动固有参数,可以通过自由振动法标定得到:加载脉冲力(控制标定力的快速加载、卸载)获得,脉冲力大小不需明确。对系统响应做低通滤波得到一阶子系统响应,根据式(17),相邻极大值或极小值的幅值比为
(26)
由上式可计算得ζ1:
(27)
相邻极大值或极小值时间间隔即为Td1,进而可得到ω1为
(28)
将ζ1、ωd1代入式(28)后,即可求得ω1。
综合以上,参数标定步骤如下:
(1)加载持续恒定标定力f0,根据系统阶跃响应计算y(x,∞),再计算η,通过y(x,∞)η/f0计算得到K1(x,lf);
(2)加载脉冲力,对系统响应低通滤波得到一阶子系统响应,标定得到ζ1、ω1;
(3)将K1(x,lf)、ζ1、ω1带入式(20)求M1。
3 实验验证
3.1 实验平台及实验步骤
实验平台由推进器、测量模块及控制模块组成,如图3所示。

图3 基于悬臂梁结构的推力测量平台结构图
推进器为冷气推进器样机;测量模块主要负责将冲击力转变为位移信号;控制模块主要用于控制测量模块及推进器工作,接收测量模块输出的位移信号以及推进器输出的入口压力值。由于建立测量模型时将冲击力等效为集中载荷,因而推进器喷口面积要小。同时,输出冲量大小在μN·s~mN·s之间,满足微冲量测量的应用背景。
测量模块及推进器如图4所示。整个推进器集成于一个平板上,喷嘴直径为1 mm。计算机接收并显示无线压力变送器发送的喷口前压力值。悬臂梁(304不锈钢,210 mm×40 mm×0.3 mm)与线圈、位移传感器探头通过同一个光学平板固定在电动位移台上,电动位移台用于调节喷口与悬臂梁之间的距离。

图4 基于悬臂梁结构的测量系统
粘贴在悬臂梁上的磁铁(Φ6 mm×1.5 mm,质量为0.29 g,材料为N35)与线圈(30匝)构成标定力产生装置。经过电子天平标定,线圈电流为0.1 A时,电磁力大小为0.511 mN。位移传感器为电容式位移传感器(分辨力为30 nm,量程为1 mm),该传感器基于变极距电容原理测量位移[17],可以直接以数字量形式输出悬臂梁位移响应。基于确定的冲量解算及参数标定方法,可确定实验步骤如下:
(1)标定M1。施加恒定标定力得到K1(x,lf),再施加脉冲力,标定得到ζ1、ω1。最后根据K1(x,lf)、ζ1、ω1,计算出M1大小。
(2)计算[y1(x,t)]max。控制推进器输出脉冲力后,对悬臂梁系统响应y(x,t)低通滤波,得到y1(x,t),求取最大值得到[y1(x,t)]max。
(3)解算冲量S大小。根据式(19),通过[y1(x,t)]max及M1求解S。
3.2 实验结果
3.2.1 参数标定
在位移测量臂长x=106 mm,采样率ωs=1.041 7 kHz,标定力f0力臂lf=174 mm时,控制线圈电流依次输出0.1、0.2、0.3 A,对应f0为0.511 、1.022、1.533 mN(斥力),然后逐渐减小到0.1 A时,悬臂梁响应如图5所示。

图5 标定力逐渐增大、减小时悬臂梁响应
由图5可得,标定力作用下,系统经过动态振动,最终稳定在新的平衡位置。卸载标定力后,系统回到初始平衡位置。不同大小f0稳态位移y(x,∞)分别等于25.310 1 、60.621 2、75.632 7 μm,可求得系统增益系数K(x,lf)=4.953×10-2。根据式(24),可计算得η=0.962 7,则K1(x,lf)=4.768×10-2。
设置线圈电流为0.1 A,快速加载、卸载电流输出脉冲力时,系统响应如图6所示。电磁脉冲力作用后,振幅围绕初始零点位置逐渐衰减。

图6 电磁脉冲力作用下悬臂梁系统响应
对系统响应频谱分析,得到ωd1=6.393 9 Hz。设计42阶、截止频率为8 Hz的fir1低通数字滤波器,滤波后系统响应及极值点如图7所示。对比图6可得,滤波前,受环境噪声及悬臂梁本身高频振动的影响,系统响应振幅虽然在总体上呈现减小趋势,但在小区间内还出现幅值增大的现象。滤波后,振动曲线变得平滑,振幅随时间连续减小。

图7 电磁脉冲力响应极值点
将图7中极值点大小及对应的时间带入式(27)、式(28),可计算得ζ1=3.2×10-3,ω1=6.393 9 Hz(平均值)。在求得K1(x,lf)、ζ1及ω1后,根据式(20)可计算得M1==4.466 1。
3.2.2 冲量解算
设置开关工作时间为18 ms,保持入口压力为0.45 MPa。设置喷口距离悬臂梁距离为24 μm(通过与扭摆测量结果对比,喷口与悬臂梁轴向距离为24 μm时,悬臂梁测量得到的持续冲击力与实际推力误差最小),推进器输出脉冲力后,悬臂梁响应滤波后如图8所示。

图8 推力脉冲力作用下悬臂梁响应曲线
与图6中电磁脉冲力响应曲线对比,图8中最大位移位于零点以下,这是因为脉冲力与电磁力作用方向相反。根据图8,可求得[y1(x,t)]max=85.419 5μm,已标定得到M1=4.466 1,则推进器脉冲力冲量大小为
(29)
保持推进器工况不变,测量5次,得到该工况下S的平均值为1.879 2×10-5N·s,标准差为3.510 9×10-7N·s。
3.2.3 误差分析
采用非接触测量方式时,由于气流的发散及反射气流对来流等的影响等因素,一部分气流并没有作用在悬臂梁上,悬臂梁测量得到的冲量值与推力器冲量实际值还存在一定误差。将作用在悬臂梁上的冲量部分的测量误差记为US1,作用在悬臂梁上的冲量值与推进器冲量误差记为US2,实际冲量测量误差记为US。
M1由K1(x,lf)、ζ1及ω1计算得到。ζ1由y1(x,t)中极值点计算得到,由式(27),极值点测量误差对ζ1影响较小,同时,ζ1通过多组相邻极值点计算得到,ζ1误差的可忽略。ωd1只与极值点间隔有关,与极值点的大小无关,ωd1误差可忽略,又ζ1误差忽略,故ω1误差忽略。因而,M1误差主要受k1(x,lf)影响,而K1(x,lf)通过K(x,lf)计算得到,K(x,lf)误差主要受标定力误差影响。标定力为1.210%,可认为K1(x,lf)误差为1.210%,则UM=1.210%。综合以上分析,US1大小为
(30)
确定US1大小后,通过实验确定进行US2大小。设置推进器相同的工况,将推进器直接搭载在扭摆横梁上进行测量。扭摆原理结构如图9所示。推力作用于横梁上时,横梁在水平面内转动,扭转角通过位移传感器测量横梁的线位移得到。

图9 扭摆原理结构图
考虑扭摆测量误差在内,扭摆测量结果为2.024×10-5N·s。将悬臂梁测量结果与扭摆结果进行对比,可得US2=-7.170%。
确定US1及SS2后,可得悬臂梁结构测量推进器脉冲力冲量误差US:
(31)
4 结论
(1)悬臂梁测量系统在结构上为无穷多个欠阻尼二阶子系统的并联,系统增益值与位移测量位置的刚度系数为倒数关系;
(2)一阶子系统脉冲响应的最大位移与脉冲力冲量大小为线性关系,线性系数大小由一阶子系统增益值、阻尼比及固有振动频率决定。求出一阶子系统响应最大位移,标定出线性系数后,即可计算出冲量大小,此时悬臂梁测量系统可视为带有噪音的二阶欠阻尼系统;
(3)一阶子系统的阻尼比及固有振动频率通过自由振动法标定得到,增益值需要根据系统增益与一阶子系统增益的比值求出。
本文将高频振动考虑在内,提出并实验验证了所提出的微冲量测量方法。通过综合分析悬臂梁本身测量冲击力误差及间接法的测量误差,得到微冲量测量的相对误差为7.30%,下一步研究重点是进一步细化误差分析。

