下承式梁拱组合连续梁桥结构敏感性参数分析
关 伟,米思颖
(1.山西省交通科学研究院,山西 太原 030006;2.中交通力建设股份有限公司,陕西 西安 710075)
梁拱组合连续梁桥根据支承形式可分为上承式、中承式、下承式,该桥型跨越能力大、结构自身刚度大,造型美观,被广泛应用于公路、铁路、市政桥梁。下承式梁拱组合连续梁桥主要应用于桥下净空受限制、不宜建造上承式、中承式梁拱组合连续梁桥(拱脚存在水平推力)的情况[1]。本文以运城市某省道上一座下承式梁拱组合连续梁桥为研究对象,选取桥梁结构的跨径布置参数及拱轴状态参数进行结构参数敏感性研究,分析出敏感性参数对结构内力状态的影响,这对以后该类型的桥梁设计具有广泛的现实意义。
1 工程概况与有限元模型
位于运城市某省道上的一座下承式梁拱组合连续梁桥桥梁跨越运城市解州镇县道X826,该县道是解州镇通往运城环城解州收费站的唯一一条主干道,县道路基宽度35 m,桥梁与县道前右交叉角度为112°,县道净空预留5.5 m。桥梁建筑高度过大,势必会增加桥梁两侧引道标高,增加工程造价,加之县道以后的拓宽需求,同时考虑桥梁景观要求,桥梁主跨须一跨跨越县道。桥梁跨径布置为(27+60+27)m下承式梁拱组合连续梁桥,桥梁全长120 m,桥梁平面位于直线段上,桥梁分左、右幅进行设计,单幅桥宽16.5 m。
采用有限元软件Midas Civil 2012 建立桥梁模型,上部结构主梁采用整体3 片T梁断面,主梁等高度1.7 m,顶板厚45 cm,悬臂长2.25 cm,悬臂端部厚18 cm,悬臂根部厚45 cm。中跨拱肋矢高9 m,矢跨比为1∶6.667,拱肋轴线为悬链线,拱脚为从主梁桥墩中心线处梁顶面凸起的两条边为曲线的三角形[2],宽度同主梁梁肋宽度,吊杆采用单索面,两榀拱肋横向连接系采用三道一字型连接。桥面铺装采用下层铺设10 cm 厚C50 钢纤维防水混凝土调平层,上层铺设10 cm 厚沥青混凝土,桥面两侧设置防撞墙,汽车荷载等级为公路-I 级。主梁、横梁、拱肋均采用空间梁单元,吊杆采用桁架单元模拟,全桥共划分490 个单元,235 个节点,结构有限元模型见图1。
图1 结构有限元模型图
2 结构敏感性参数分析
2.1 桥梁跨径比例分析
以实例桥梁跨径60 m 为基础,中跨设置拱肋,拱肋矢高9 m,矢跨比为1∶6.667,拱肋轴线为悬链线,分别采用边、中跨比例为0.2、0.3、0.4、0.45、0.5、0.6、0.7 对结构进行建模,计算结构在成桥状态恒载作用下主梁产生的弯矩、活载作用下主梁产生的挠度,计算结果见图2、图3。
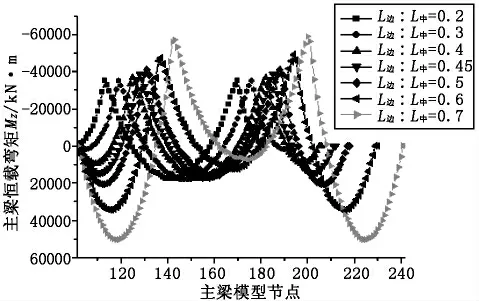
图2 主梁恒载弯矩Mz图
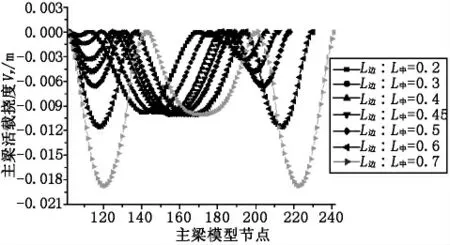
图3 主梁活载挠度Vy图
从图2可以看出,随着边、中跨跨径比例的增大,边跨弯矩呈增大趋势。当边、中跨比例为0.2 时,边跨全部承受负弯矩;当边、中跨比例在0.4~0.5 之间时,边跨弯矩增幅为45%,较其他边、中跨比例增幅小。支点负弯矩绝对值呈增大趋势,中跨正弯矩呈减小趋势,当边、中跨比例在0.4~0.5 之间时,中跨正弯矩增幅为5%。从图3 可以看出,随着边、中跨跨径比例的增大,边跨主梁挠度呈增大趋势,当边、中跨比例在0.4~0.5 之间时,边跨挠度增幅为40%。中跨挠度基本不变。
三跨下承式梁拱组合连续梁桥,由于在中跨采用钢管拱对主梁进行加劲,中跨主梁弯矩通过梁拱间的吊杆转化为拱的轴向压力,中跨弯矩会降低。由于边跨受中跨拱刚度的影响,随着边、中跨比例的增大,边跨跨径增大,边跨弯矩增大,由负弯矩变化为正弯矩,主梁支点负弯矩绝对值增大,中跨正弯矩减小。成桥状态下主梁在活载作用下,边跨跨径增大,主梁挠度会增大,而中跨由于钢管拱对主梁进行加劲,中跨挠度基本不变。因此,在设计当中,梁拱组合连续梁桥边、中跨比例在0.4~0.5 之间是合适的[1],且主梁边、中跨正弯矩接近,这样有利于主梁配置钢束。
2.2 梁拱刚度分析
建立跨径为(27+60+27)m 的连续梁和梁拱组合连续梁模型,比较主梁在有拱与无拱情况下在恒载作用下主梁弯矩和活载作用下主梁挠度的变化,计算结果见图4、图5。

图4 主梁有拱和无拱恒载弯矩Mz图

图5 主梁有拱和无拱活载挠度Vy图
从图4 可以看出,主梁无拱时跨中正弯矩为45 682 kN·m,有拱时跨中正弯矩为10 642 kN·m,无拱时是有拱时的4.293 倍。主梁无拱时支点负弯矩为75 592 kN·m,有拱时支点负弯矩为25 179 kN·m,无拱时是有拱时的3.002 倍。由此可见,梁拱组合连续梁桥拱肋的存在极大地改善了主梁的受力状态,梁拱组合连续梁桥结构将主梁的弯矩通过梁拱间的吊杆转化为拱肋的压力,充分发挥了拱肋的受压性能,有效地降低了主梁的弯矩。从图5 可以看出,在活载作用下梁拱组合结构主跨跨中挠度较无拱时主梁减少很多,无拱时主梁中跨挠度约为有拱时的3.873 倍,可见拱肋的刚度对主梁的刚度贡献较大。
拱肋的抗弯刚度Ka与主梁的抗弯刚度Kb,当Ka>Kb时可不计梁的刚度,弯矩全部由拱肋来承担,即系杆拱。当10Ka<Kb时可不计拱的刚度,弯矩全部由主梁来承担,即柔拱刚梁。在上述二者范围之内时,即刚拱刚梁,弯矩由主梁及拱肋按刚度分担[1]。
2.3 拱轴线拱轴系数m 对拱肋、主梁影响分析
通过调整拱轴线拱轴系数来查看其对结构行为的影响,在桥梁中跨拱肋矢高9 m 不变的情况下,拱轴系数分别取1.5、2.5、3.5、4.5、5.5 数值,分别计算成桥状态恒载作用下拱肋、主梁结构的内力状态。取沿路线前进方向左侧半拱肋为研究对象,不同拱轴系数拱肋轴线纵坐标、拱肋弯矩、拱肋轴力、主梁弯矩见图6~图9。
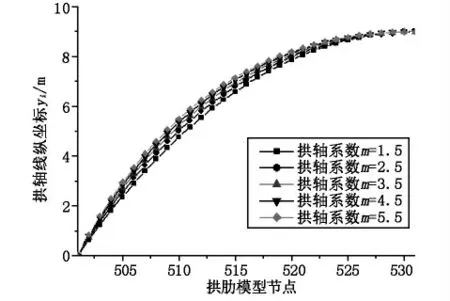
图6 拱轴系数变化拱轴线纵坐标yi图
从图6 可以看出,随着拱轴系数m 的增大,半拱拱轴线纵坐标呈增大趋势,由于拱肋矢跨比不变,拱脚及拱顶拱轴线纵坐标不变,拱肋轴线其余节点纵坐标呈增大趋势,半拱轴线长度增长,半拱轴线由陡变坦,增幅较大区域从拱脚起在半拱长度1/4点~1/2 间,半拱轴线纵坐标最大增加16.9%。
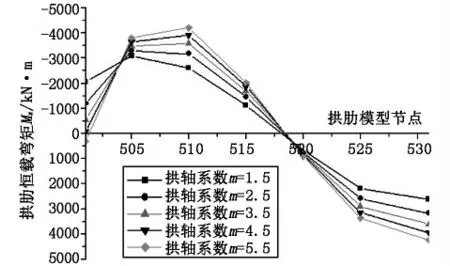
图7 拱轴系数变化拱肋恒载弯矩Mz图
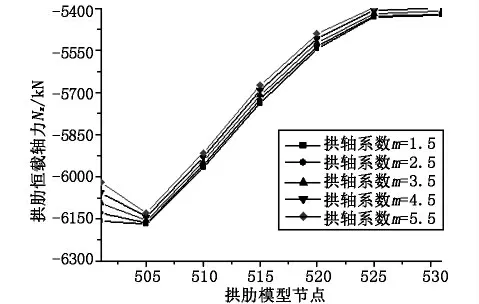
图8 拱轴系数变化拱肋恒载轴力Nx图

图9 拱轴系数变化主梁恒载弯矩Mz图
随着拱轴系数m 的增大,从图7 可以看出,成桥状态下拱肋在恒载作用下,半拱1/4 点、拱顶处弯矩绝对值均呈增大趋势。半拱1/4 点处弯矩呈现负弯矩,拱肋顶缘受拉、底缘受压,拱轴系数m=1.5 增大至拱轴系数m =5.5,半拱1/4 点处负弯矩增大61.2%。半拱拱顶弯矩呈现正弯矩,拱肋顶缘受压、底缘受拉,拱轴系数m=1.5 增大至拱轴系数m=5.5,半拱拱顶处正弯矩增大61.9%。从图8 可以看出,拱肋各节点轴力呈减小趋势,随着拱轴系数的增大,拱肋节点轴力减少2.2%。从图9 可以看出,主梁边跨最大正弯矩、支点负弯矩、跨中正弯距绝对值均呈增大趋势,分别增加8.2%、5.1%、1%。
拱轴系数的增大使从拱脚起在半拱长度1/4点~1/2 区间内拱轴线凸起较明显,对该区段拱肋负弯矩及半拱拱顶正弯矩影响较大,对主梁边跨最大正弯距、支点负弯矩、中跨正弯距影响较小。当拱轴系数m=5.5 时,拱脚出现正弯矩,表明拱脚内侧受拉,这在设计当中应予以重视,悬链线拱轴线拱轴系数在设计中选取时不宜大于3.5[3]。
2.4 拱轴线矢高f对拱肋、主梁影响分析
通过调整拱轴线矢高来查看其对结构行为的影响,在桥梁拱肋拱轴线拱轴系数为1.5 不变的情况下,矢高分别取8 m、9 m、10 m、11 m、12 m 数值,分别计算成桥状态恒载作用下拱肋、主梁结构的内力状态。取沿路线前进方向左侧半拱肋为研究对象,不同拱肋矢高拱轴线纵坐标、拱肋弯矩、拱肋轴力、主梁弯矩见图10~图13。
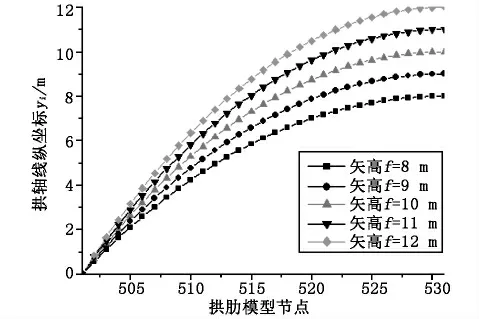
图10 拱轴线纵坐标yi图
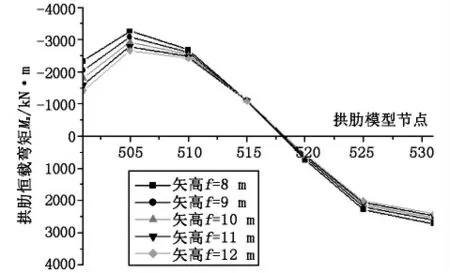
图11 拱轴矢高变化拱肋恒载弯矩Mz图

图12 拱轴矢高变化拱肋恒载轴力Nx图
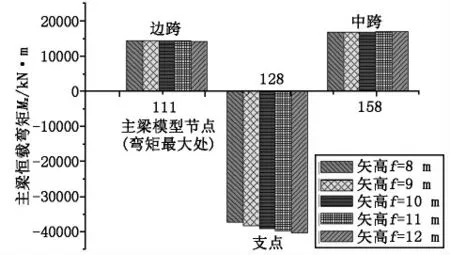
图13 拱轴矢高变化主梁恒载弯矩Mz图
从图10 可以看出,随着矢高f 的增大,半拱拱轴线纵坐标呈增大趋势,半拱轴线长度增长,半拱轴线由坦变陡,半拱拱顶纵坐标增幅最大。随着矢高f的增大。从图11 可以看出,成桥状态下拱肋在恒载作用下,拱肋各节点弯矩绝对值均呈减小趋势,半拱1/4 点、拱顶处弯矩绝对值均变化较大,半拱1/4 点处表现为负弯矩,拱顶处则为正弯矩。从图12 可以看出,半拱轴力各节点轴力表现为轴向受压,其绝对值呈减小趋势,拱轴同一节点在不同矢高情况下,轴力差值呈减小趋势。从图13 可以看出,主梁边跨最大正弯矩呈减小趋势,减小0.99%。主梁支点负弯矩、跨中正弯矩绝对值均呈增大趋势,分别增加8.1%、1.6%。
拱肋矢高的增大使拱肋1/4 点处负弯矩、半拱拱顶正弯矩都有所降低,并且使拱肋轴向压力减小,但是增幅呈减小趋势。对主梁边跨最大正弯矩几乎无影响,对主梁支点负弯矩、跨中正弯矩影响较小。可见矢高的增大在一定范围内变化对拱肋内力状态是有益的,矢高越大会使拱肋轴线变陡,桥梁景观效果变差,悬链线拱轴线在设置拱肋跨的矢高一般取值在跨径的1/5~1/8[1]。
3 结语
a)下承式梁拱组合连续梁桥由于采用钢管拱对主梁进行加劲,主梁弯矩通过梁拱间的吊杆转化为拱的轴向压力,主梁弯矩降低,该桥型结构合理,跨越能力大,桥梁景观效果强。
b)桥梁主梁边、中跨比例在0.4~0.5 之间是合理的。减小或增大边跨跨径会使边跨弯矩与中跨弯矩相差较大,不利于主梁钢束的配置,减小边跨跨径会使边跨主梁承受负弯矩,增大边跨跨径会使边跨主梁挠度增大,对结构不利。
c)拱轴系数对半拱长度1/4 点~1/2 区域拱的内力影响较大,悬链线拱轴线拱轴系数在桥梁设计中选取时不大于3.5 为宜。
d)拱轴矢高的选取会影响桥梁整体的景观效果,悬链线拱轴线在设置拱肋跨的矢高取值在跨径的1/5~1/8 为宜。
e)下承式梁拱组合连续梁桥结构采用杆系结构进行整体分析,拱脚处结构应力计算结果失真,由于拱脚处结构应力状态较复杂,在设计当中须采用实体单元模拟进行分析,以便掌握梁拱结合部即拱脚处真实应力状态,为设计、施工提供依据。

