基于改进主成分分析法的城市需水量预测*

(新疆塔里木河流域希尼尔水库管理局，新疆 库尔勒 841000)

城市需水量预测是进行区域水资源调配的重要基础，其受人口、固定资产投资、经济增长等多种因素的影响，且具有非线性、大时滞和不稳定等特点。因此对城市需水量预测方法进行研究，及时准确掌握未来城市需水量的变化规律，对于提高城市供水保证率、降低城市缺水风险、维护水安全具有重要意义。

目前，国内外学者针对城市需水量预测方法已经进行了大量的研究，取得了一定的成果。如：采用灰色关联模型、主成分回归模型、多元线性回归模型、神经网络模型等[1-5]，但这些方法在处理数据上缺少鲁棒性，导致模型普遍缺乏长效性和扩展能力，不能完全反映数据的本质特征。

鉴于此，本文在前人研究的基础上，以新疆阿克苏市历年城市需水量及相关数据为例，耦合主成分分析(Principal Component Analysis, PCA)和长短时记忆神经网络(Long Short-term Memory，LSTM)的各自优点，构建了基于PCA-LSTM模型的城市需水量预测方法，并取得了一些有价值的研究成果。

1 研究方法

1.1 主成分分析法

PCA方法的主要计算步骤如下：ⓐ原始数据标准化处理；ⓑ计算标准化矩阵的相关系数；ⓒ根据相关系数矩阵计算特征值和特征向量；ⓓ计算特征值及贡献率；ⓔ计算主成分载荷矩阵及得分。具体计算过程参见文献[4]。

1.2 长短时记忆神经网络

LSTM模型具体算法过程参见文献[6]。

1.3 改进主成分分析法的城市需水量预测模型

本文耦合PCA模型与LSTM模型的各自优点，构建了PCA-LSTM模型。其计算步骤如下：ⓐ对历年城市需水量和相关数据进行标准化处理； ⓑ利用PCA降低模型输入参数维度，筛选出需水量的关键因子； ⓒ构建PCA-LSTM预测模型，并对样本参数不断进行优化； ⓓ评价模型性能。

1.4 模型评价指标

选用平均绝对误差(Mean Absolute Error，MAE)、均方根误差(Root Mean Squard Error，RMSE)和平均绝对百分误差(Mean Absolute Percent Error，MAPE)3项指标作为模型优劣评价指标。

2 结果分析

2.1 数据准备

以新疆阿克苏市2000—2016年城市需水量数据为研究对象，采用已经预处理过的试验数据，主要包括全市历年GDP、第一产业增加值、固定资产投资、城镇消费品零售额、总人口、城镇居民人均可支配收入、城市绿化面积和城市需水量数据。以2000—2012年数据为训练集，2013—2016年数据为验证集。

为了进一步提高模型计算结果的可信度，将所构建模型(PCA-LSTM模型)与LSTM模型、粒子群优化BP神经网络与最小二乘支持向量机模型计算结果进行对比研究。

2.2 结果分析

2.2.1 仿真分析

利用SPSS软件计算影响城市需水量的主次因素，主成分计算结果见表1。由表1可以看出，前3个因子的特征值均大于1，且累计贡献率达到83.47%，因此选择前3个因子代替原变量。通过正交旋转法得到各因素对3个主成分的载荷，见表2。对第1因子贡献最大的为全市GDP、第一产业增加值；对第2因子贡献较大的是固定资产投资；城市总人口对第3因子贡献较大。

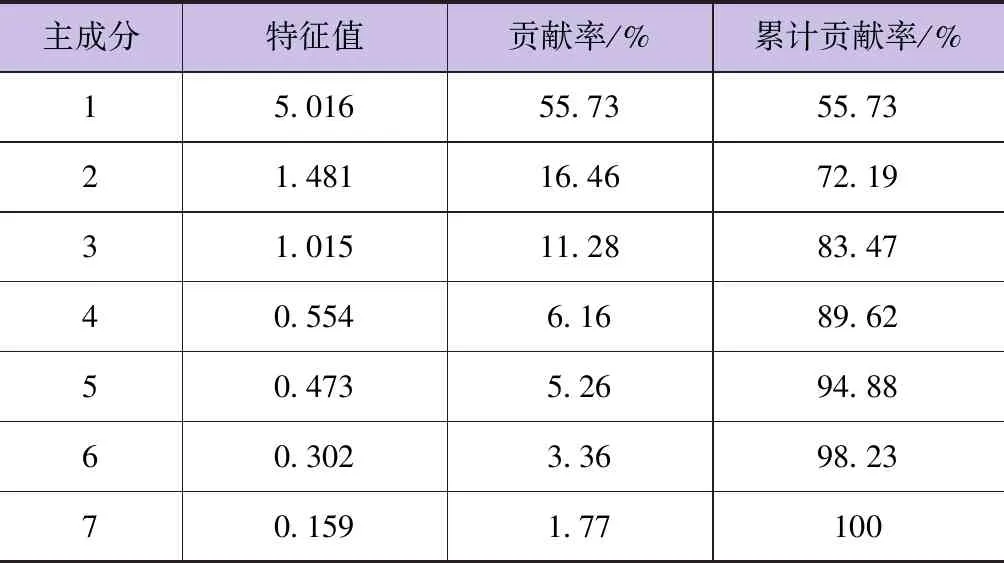
表1 特征值及主成分贡献率

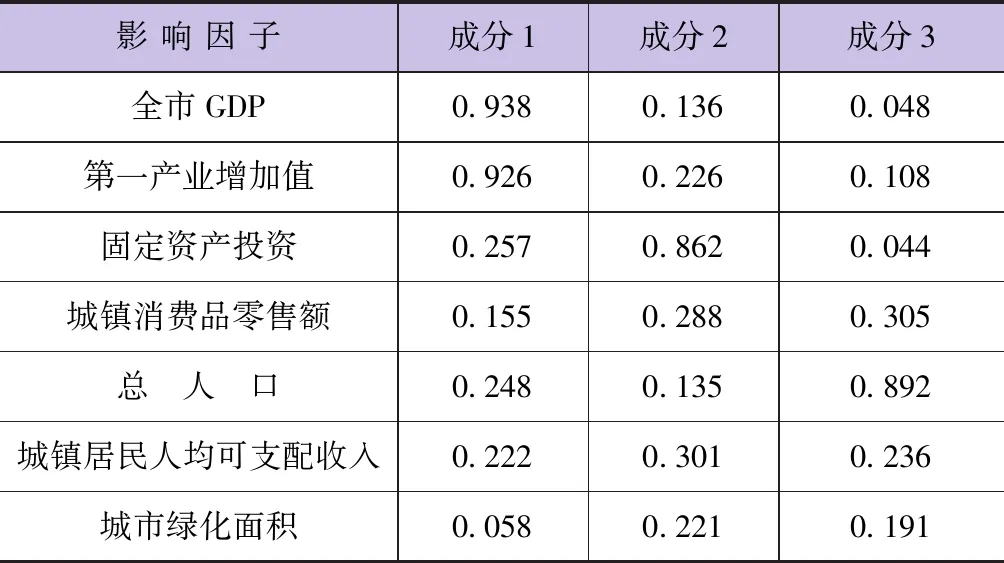
表2 主成分矩阵

因此，本研究选用的主要影响因子有全市GDP、第一产业增加值、固定资产投资与城市总人口，并以此构建未来城市需水量预测模型的输入样本，输出参数为1年后的城市需水量。模型具体参数详见表3。

表3 PCA-LSTM算法参数

由表4可以看出，构建模型的评价指标MAE、MAPE和RMSE分别达到了12.75万m3、0.06%和15.11万m3，证明该模型预测精度较为理想。

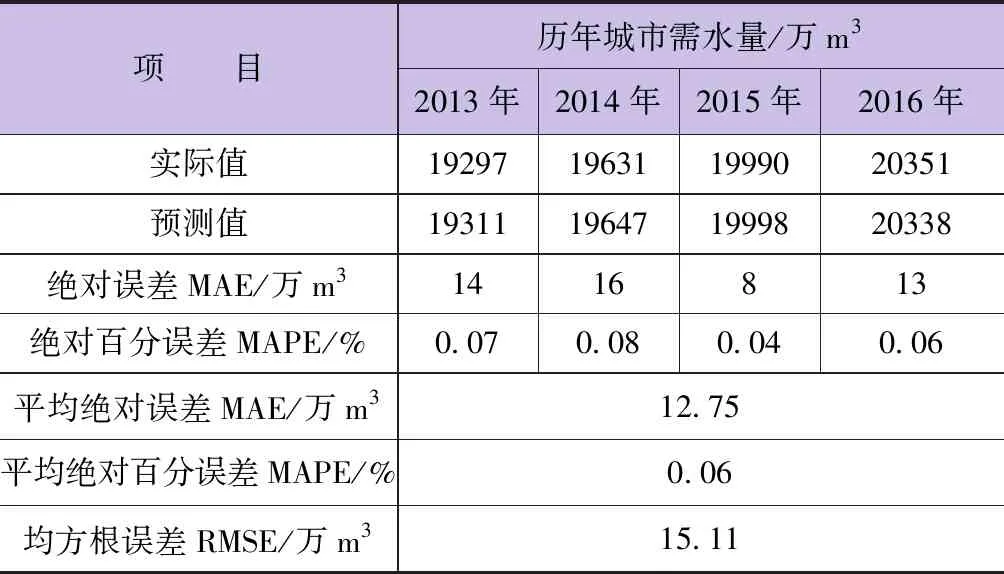
表4 PCA-LSTM预测模型精度分析

2.2.2 模型对比

LSTM模型、PCA-BP模型、PCA-LSSVM等模型计算结果详见表5。

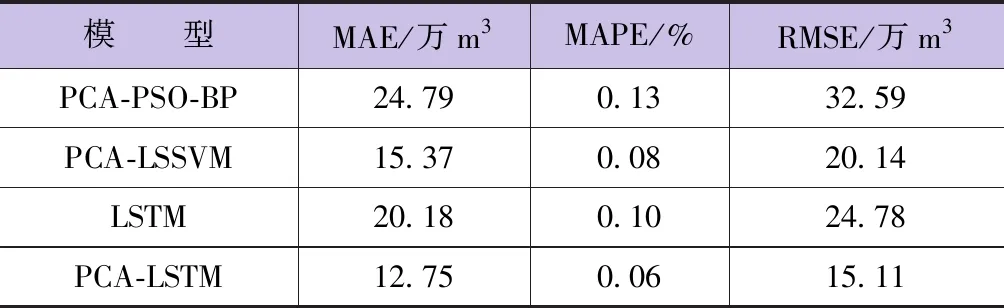
表5 不同模型预测结果精度分析

由表5可知，PCA-LSTM模型的MAE、MAPE和RMSE分别为12.75万m3、0.06%和15.11万m3，较LSTM模型分别提高了7.43万m3、0.04%和9.67万m3的精度，而且评价指标优于PCA-PSO-BP与PCA-LSSVM模型。这表明PCA-LSTM模型可为干旱区城市水资源调度调控提供决策依据。

3 结 论

a.利用PCA方法筛选影响城市需水量的主要因子，实现了模型有效降维，提升了LSTM模型的预测精度和稳定性。

b.构建的PCA-LSTM模型与BP神经网络等其他模型相比，模型评价指标MAE、MAPE和RMSE的误差分别为12.75万m3、0.06%和15.11万m3，均优于传统模型，为干旱区城市水资源调度调控开辟了新方法。