直升机静力试验杠杆加载系统的自动化设计

陈庆童，杨广根，杨 磊，王卫卫

(中国直升机设计研究所，江西 景德镇 333001)

0 引言

直升机的全机或部件结构静力试验是研究全机或部件结构在静载荷作用下的静强度特性，其目的是通过试验来验证结构能否满足设计和强度规范要求[1-5]。由于试验条件的限制，大型静力试验往往需要通过少数加载作动器实现对众多加载点的加载，这就需要大量采用杠杆系统加载以满足加载要求。但是，在杠杆加载系统中，由于杠杆加载系统存在自重，在试验加载过程中必然会对试验件产生附加力，而直升机结构静力试验要求施加等量载荷(实际加载值等于理论载荷值)，因此，在静力试验中必须通过施加配重的方法将加载杠杆系统附加力的影响降到最小。

在大型静力试验中，传统设计方法效率低，容易出错，重复性计算工作量大，且杠杆系统建模装配繁琐费时。因此，本文基于EXCEL VBA技术，采用用户交互式输入界面，结合杠杆原理和载荷系数法，对杠杆系统的各参数(诸如杠杆长度、杠杆合力点坐标、杠杆型号、加载端的配重大小、杠杆系统自身固重、实际加载载荷等)以及杠杆系统的配重进行了VBA程序开发，并结合CATIA二次开发技术，以VBA程序所得结果为建模参数，驱动CATIA软件完成杠杆系统的自动建模和自动装配，从而实现整个杠杆系统的自动化计算和自动化建模，完成杠杆加载系统的自动化设计，极大地提高了试验设计人员的设计效率和设计精度，同时还便于检测杠杆系统的干涉情况以及与试验结构的组装。本文最后通过计算实例验证了该VBA程序的正确性和高效性。

1 VBA和CATIA二次开发简介

Visual Basic for Applications，统称VBA，它是新一代标准宏语言，是基于Visual Basic发展而来的，二者具有相似的语言结构。VBA不但继承了VB的开发机制，而且它们的集成开发环境IDE(Integrated Development Environment)也几乎相同。Visual Basic作为一套独立的Windows系统开发工具，可用于开发Windows环境下的各类应用程序，是一种可视化的、面向对象的、采用事件驱动方式的结构化高级程序设计语言,具有高效率、简单易学及功能强大的特点。经过优化，VBA专门用于Office办公软件各组件的应用开发[6]。

CATIA接口可以通过两种方式与外部程序通信：进程内应用程序(In—Process Application)方式和进程外应用程序(Out—Process Application)方式[7]。进程内访问是指程序脚本和CATIA在同一进程内执行，这一方式主要通过CATIA的宏(Macro)命令运行。宏的方法比较简单，在CATIA环境中即可操作。但宏在运行过程中不能接受输入，无法改变参数值，智能程度较低，只适用于简单的重复性操作过程。进程外开发方式主要的有两种方法：一种是开放的基于构件的应用编程接口CAA V5技术；另一种是自动化对象编程CATIA Automation技术。前者是基于CATIA已有组件的定制开发，后者是交互方式的定制开发。两者的共同特点是程序脚本均由第三方软件开发，通过CATIA提供的连接组件实现两者之间的通信。本文主要是基于CATIA Automation技术，利用VBA语言对CATIA进行二次开发。

2 程序计算原理

2.1 杠杆参数计算

对于如图1所示的杠杆来说，不考虑杠杆系统的自重，杠杆长度为(a+b)，两端受力为PA、PB，则可以通过式(1)-式(4)得出杠杆系统的有关参数：

P=PA+PB

(1)

a=(a+b)·PB/P

(2)

b=(a+b)·PA/P

(3)

M=PA·a=PB·b

(4)

式中，P为杠杆合力点所受载荷大小；M为杠杆所受的弯矩。

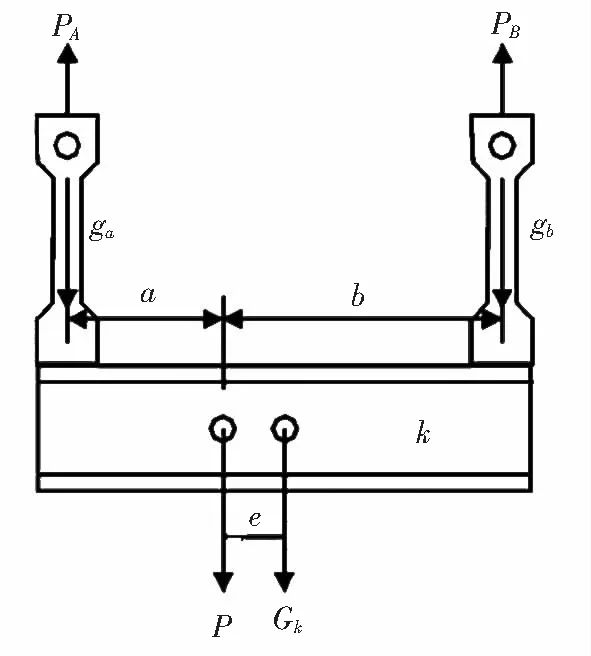
图1 杠杆作用示意图

2.2 配重计算

在静力试验中常用的配重计算方法有力矩法和载荷系数法。

2.2.1 力矩法

图1表示一杠杆，重量为G，重心在g点。杠杆两端作用f1、f2两个力，其合力作用点O点.但是一般O点与g点不重合，从而产生配重问题。当f1、f2已知时，得不平衡力矩M=G*e：若在a点加一向下配重ΔGa=M/la，则g与O重合，ΔGa称为正配重，P=f1+f2-G-ΔGa；若在b点加一向上配重ΔGa=M/lb，则g与O重合，ΔGa称为负配重，P=f1+f2-G+ΔGb。

以上即为力矩法配平的过程。此法的缺点是，需逐级配平，配重数量多，不利于大型杠杆加载系统的配重计算。

2.2.2 载荷系数法

基于力矩法的缺点，本文采用载荷系数法对杠杆系统进行配重计算。

图1中所示杠杆k，重量为Gk，连接件重量左端为ga，右端为gb，外载PA与PB，则Gk、ga、gb分到A、B的重量分别为：

(5)

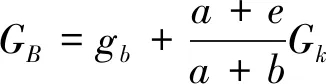
(6)

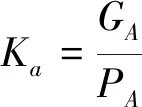
(7)

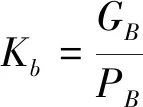
(8)

取KO为公共值，由

KO=(GA+ΔGA)/PA=(GB+ΔGB)/PB

(9)

得：

ΔGA=(K0-Ka)PA

(10)

ΔGB=(K0-Kb)PB

(11)

P=(1-K0)(PA+PB)

(12)

式中，ΔGi为配重，Ki=Gi/Pi称为载荷系数。当各Ki均达K0时，Gi+ΔGi=K0Pi，即加配重后的重量与载荷分布相同，也即杠杆的重心与合力作用点重合。以上方法即成为载荷系数法[8-9]。

载荷系数法可以毫无困难地应用于复杂的杠杆系统。杠杆系统图见图2。

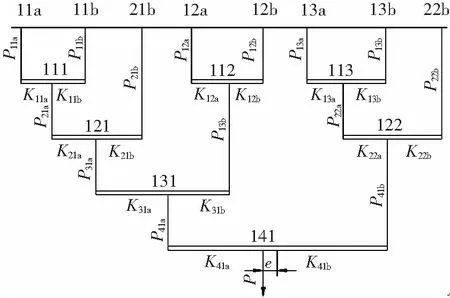
图2 杠杆系统图

图2中，P代表杠杆系统的设计载荷；Pija、Pijb代表每根杠杆的设计载荷；Kija、Kijb代表每根杠杆加载点的载荷系数；lij为杠杆的编号;

在图2所示杠杆系统中，对于杠杆l11来说，由于受杠杆重量G11和杠杆两端连接件重量g11a、g11b的影响，在11a和11b点引起的附加力分别为：

(13)

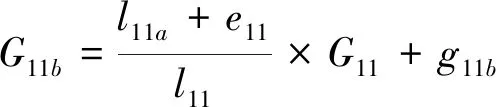
(14)

K11a=G11a/P11a

(15)

K11b=G11b/P11b

(16)

依此类推，对于杠杆l41：

(17)

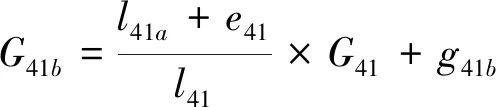
(18)

K41a=G21a/(P11a+P11b+P12a+P12b+P21b)

(19)

K41b=G21b/(P13a+P13b+P22b)

(20)

又根据杠杆加载原理，当41a点加了K41a倍的设计载荷时，与它连接的载荷作用点11a、11b、21a、12a、12b等点上也引起了K41a倍的设计载荷。

把对杠杆l41的结果推广到整个杠杆系统，并假设每级杠杆两端的载荷系数均已求得，整个杠杆系统重量在载荷作用点11a上引起的附加力：

R11=K11a×P11a+K21a×P11a+K31a×P11a+

K41a×P11a=(K11a+K21a+K31a+K41a)×

P11a=ξ11a×P11a

(21)

式(21)中,ξ11a称为11a点的“总载荷系数”。如此类推，各载荷作用点的总载荷系数等于与它相连的各杠杆臂的载荷系数之和。

配重计算就是要求出使各载荷作用点之总载荷系数相等而应加在各加载点的配重值。设各载荷作用点的总载荷系数为ξij，根据经验选出一适当的ξ0作为公共值。则各载荷作用点需加的配重为：

Gij=(ξ0-ξij)×Pij

(22)

式(22)中,Pij为该点的设计载荷。

一般ξ0的选择以少加配重或少加反配重为原则，即一般应为ξij的中间值或最大值。

2.3 CATIA参数化建模

对于杠杆的三维CATIA模型的自动生成，本文采用的是CATIA参数化建模功能。CATIA v5具有完善的系统参数自动提取功能，它能在草图设计时将设计人员输入的尺寸约束作为特征参数保存起来，并且在此后的设计中可视化地对它进行修改，从而达到参数驱动建模的目的。本文将VBA程序所得出的结果作为输入参数，驱动CATIA软件中杠杆模型的特征参数，完成杠杆模型的建立(图3)。

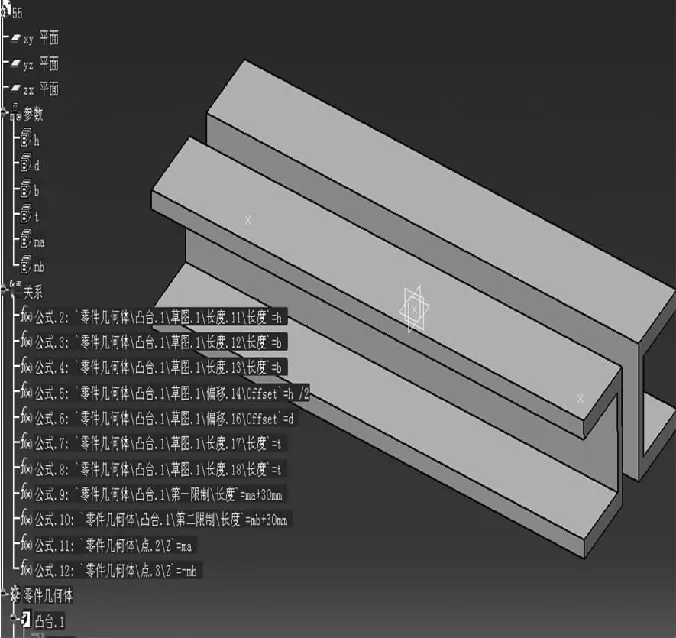
图3 杠杆参数化模型

3 程序实现

由于前期的载荷系数法中对杠杆加载系统中的加载点、加载杠杆以及连接件的编号都是规则化的，这为程序的实现提供了可行性。对于该程序的实现，主要分为五步：

第一步：根据杠杆原理，求出杠杆系统各杠杆的参数，比如杠杆长度，杠杆合力点位置，杠杆型号以及杠杆合力点到杠杆两端的距离。

第二步：生成各级杠杆CATIA零件图。首先建立包括杠杆长度和槽钢型号参数等杠杆结构参数化模型(如图4所示)，如槽钢高度参数h、槽钢腰厚参数b、腿宽参数d以及合力点与杠杆两加载端距离参数la和lb等。以参数化模型为基础，根据第一步的计算结果，对模型进行尺寸驱动，然后不断存储新文件即可生成各级杠杆。

第三步：生成杠杆系统空间位置关系图。根据当前参数下的杠杆系统的分布情况，画出各级杠杆的空间位置，显示其几何关系。

第四步：杠杆系统的装配。将各个杠杆模型与杠杆关系图装配，装配需要满足2个约束条件：杠杆模型两孔中心点与杠杆系统空间位置关系图对于端点重合；槽钢腰厚平面与杠杆关系图杠杆平面平行。

第五步：杠杆系统配重计算。若杠杆系统为z向杠杆，则程序根据载荷系数法原理进行配重计算。

至此，本程序完成了对静力试验杠杆加载系统从参数计算到三维数模的生成，以及配重的计算。图4为本文计算方法流程图。

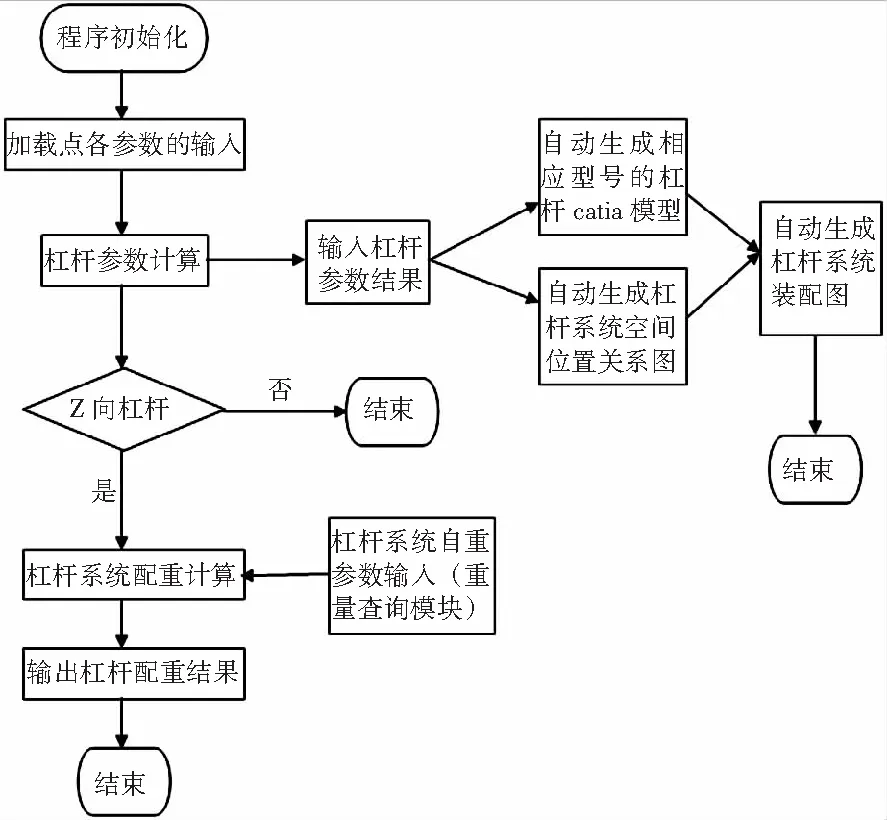
图4 程序流程示意图

4 应用实例

某复合材料整体件静力试验是单点悬吊、多点协调加载的大型静力试验。其各个方向的杠杆系统总数多达近20个。由于试验采用的是单点悬吊的承载方式，如果在试验加载过程中出现不平衡力或力矩，试验件就无法保持平衡。传统计算及设计方法效率较低，为前期试验设计带来很大的工作量，延长了试验设计周期。而利用本程序对该大型试验杠杆加载系统进行自动化设计，仅需数分钟就可完成以往数天的工作量，能极大地提高工作效率，缩短试验设计周期。下面以该复合材料整体件静力试验杠杆加载系统的设计为例进行说明。

表1为该杠杆加载系统中的某一组杠杆(F3375-F3900联合杠杆)的参数。图5为该联合杠杆输入示意图。表2和表3为利用VBA程序得出的该组联合杠杆计算结果以及配重结果。图6为该程序自动输出杠杆3D模型。图7为该组联合杠杆的空间位置关系图，图8为该组联合杠杆的装配图，图9为该复合材料整体件静力试验杠杆加载系统自动化设计完成以后的装配图。

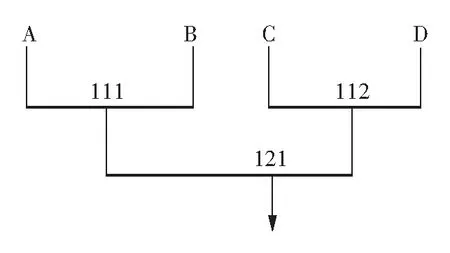
图5 杠杆系统示意图

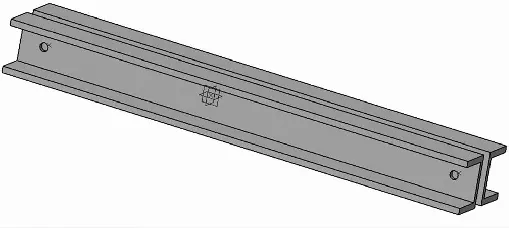
图6 杠杆l11 CATIA 3D模型

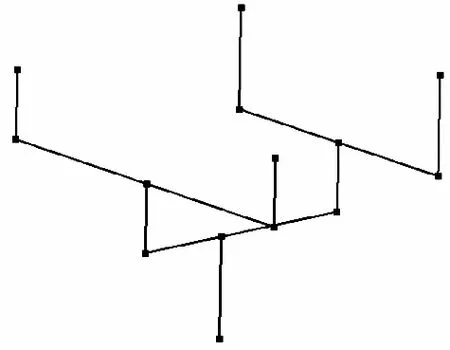
图7 杠杆加载系统中的某一组杠杆的空间位置关系图

图8 杠杆加载系统中的某一组杠杆的装配图

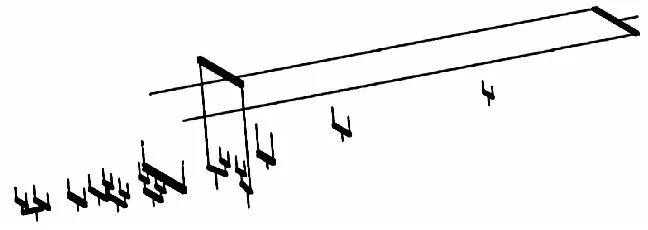
图9 复合材料整体件静力试验杠杆加载系统装配图

名称加载点名称加载点坐标加载点自重/(N)所受载荷大小/(N)F3375-F3900联合杠杆A(3374.455,-321.371,2089.644)79.793185B(3374.455,321.371,2089.644)753185C(3900,-424,2021.446)3514826D(3900,414,2021.466)357.74952

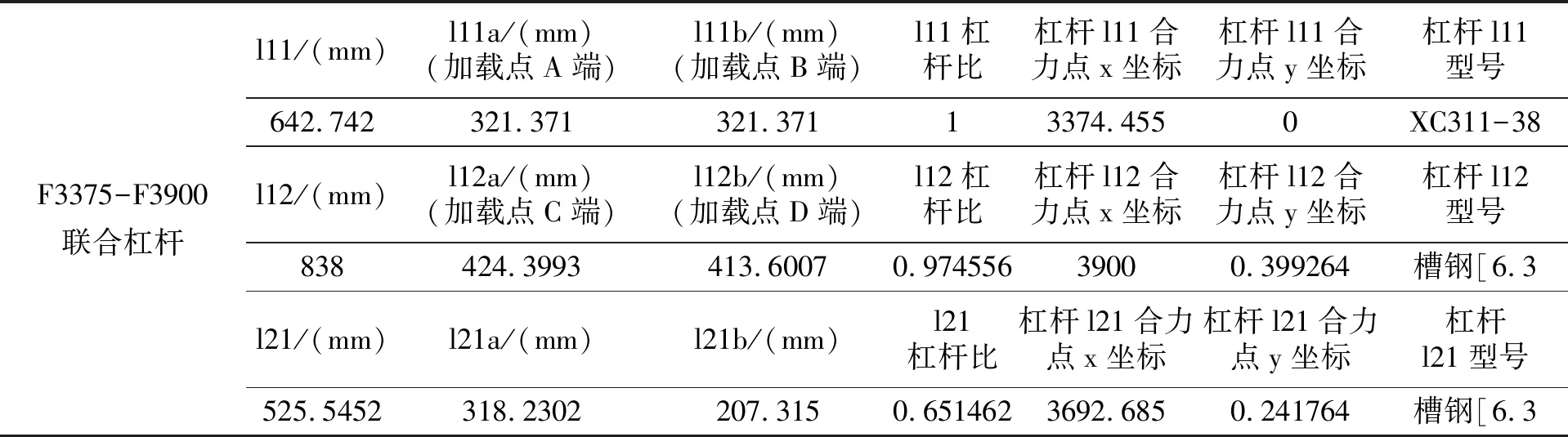
表2 VBA程序计算杠杆参数结果

表3 VBA程序计算杠杆系统配重结果

采用本文程序对该试验的杠杆加载系统进行自动设计后，经试验验证，结果显示试验测量应变数据与理论计算值基本相近，试验加载过程中试验件的三个姿态角始终处在误差范围内，试验件保持平衡，证明了程序自动设计的有效性。

5 结论

在直升机大型静力试验过程中，杠杆加载系统的设计和计算是一项必不可缺的内容，而整个试验包括十几组杠杆系统，每组杠杆系统又分多级，因此，传统的杠杆系统设计方法非常繁琐，且效率低下。本文基于EXCEL VBA技术和CATIA二次开发，通过交互式用户输入界面，可以方便地计算出各级杠杆参数以及杠杆系统的配重，并且能自动生产杠杆系统的三维CATIA模型。通过具体的实例，说明了本文提出的方法能极大地提高杠杆加载系统设计的效率，缩短前期的试验设计时间。本程序除了能保证加载精度、杠杆强度外，还可以检查杠杆系统的干涉情况以及与试验结构的组装。