基于全载荷的整体式立体仓库货架强度分析
王素玉,鹿国庆,曹冲振,许彤然,徐 杰
WANG Suyu,LU Guoqing,CAO Chongzhen,XU Tongran,XU Jie
(山东科技大学 交通学院,山东 青岛 266590)(College of Transportation,Shandong University of Science and Technology,Qingdao 266590,China)
1 仓库概述
某整体式立体仓库位于我国西北地区,存放货物的形式为箱式货物。仓库的允许建筑面积为45亩,即建筑面积为29 700m2,其基本建筑类型为钢结构建筑,立体库货架所采用的钢结构材料为Q235。货架纵向(沿巷道)总长度为96.1m,总宽度为36.5m,总高度为21.8m。其中单排高密度货架宽度为1m,巷道宽度为4m。
2 货架结构
结构设计的核心问题就是围绕着如何设计、制造、安装一个高精度的货架、以保证货架在长期使用下保证具有一定的刚度、强度和稳定性之外,还需满足精度要求而展开的[1]。整体式立体仓库货架的主要功能是对货物进行存储,它的存储单元均为托盘系输送单元,对于立体仓库的货架,应以保证高保有量原则为主,所以立体仓库货架应采用多排的高密度货架,使用双托盘位的存放方法,既增加了保有量又减少了货架材料的使用。
综合立体仓库货架的设计与布局、对所有的货架布置进行整体规划和对货架整体运用三维软件进行建模如图1所示。
对立体仓库货架参数进行标定,具体设计技术参数如表1。

图1 货架整体三维建模
3 货架载荷分析
库内选用整体式高密度货架,其基本建筑类型为钢结构建筑。立体库货架钢结构材料采用Q235,钢结构建筑在设计过程中的稳定性问题、强度问题极为重要。全载荷指货架受货物载荷、风载、雪载以及地震载荷等组合载荷,对于所选货架进行静力学全载荷分析,能有效判断其刚度强度。
该立体仓库每列货架顶部用横梁与每个立柱通过4个高强度螺栓连接,如图2,横梁的尺寸为方钢110mm×110mm×7mm;横梁上端的竖直梁通过2个高强度螺栓固定在横梁上。斜梁H型钢与每个竖直梁用2个高强度螺栓连接,竖直梁尺寸为方钢80mm×80mm×5mm,斜梁H型钢尺寸为 100mm×50mm×5mm。
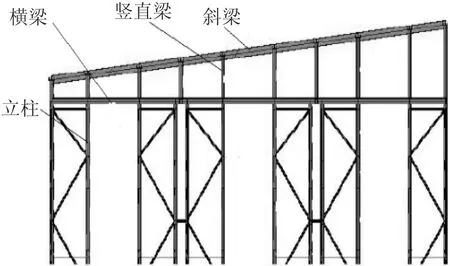
图2 整体式立体仓库货架局部结构图
根据货格的承载要求,每个货格承载两托货物,重量共为1 500kg。如图3,单个货格有4个承载节点,所以满载时每个节点承载375kg。但是考虑到相邻两个货格共用两个立柱,故此时两个立柱上的节点承载应为375×2=750kg,且节点两侧所产生的弯矩互相抵消。如图4,立体库的第一列和最后一列的外侧承载节点由于只承受一个货格的承载重量,所以承载节点承受货物重量375kg,且承载节点还受弯矩的作用。

图3 中间货格受力图

图4 两端货格受力图
(1)中间货格载荷计算

式中:F1—中间节点载荷,N;γQ—可变载荷的分项系数,取值为1.4;m1—承载节点承受货物重量,kg;g—重力加速度,m/s。

(2)两端货格载荷计算

式中:F2—两端节点载荷,N;γQ—可变载荷的分项系数,取值为1.4;m2—承载节点承受货物重量,kg;g—重力加速度,m/s。

(3) 两端弯矩计算

式中:F2—第一列与最后一列的外侧承载节点所受弯矩,N·mm;l—横梁的长度,mm。

3.1 风载能力计算
所设计的立体仓库地处西北地区,风沙现象较为严重,风压系数为0.35kN/m2,整体式立体仓库可能承受风载的面有3个,计算时选取两个面积较大的迎风面进行计算,其中一个是选取货架的第一排迎风面,另外一个是货架的第一列迎风面。
垂直于建筑物表面上的风载荷标准值计算公式[2]为:

式中:Wki—风载荷标准值(N/m);βz—高度z处的风振系数(根据货架钢结构的外形尺寸,可以不考虑风振系数,故取值为1)[3];μs—风载荷体型系数(钢结构的类型为封闭式单坡屋面,风载荷体型系数为0.8)[4];μzi—风压高度变化系数;W0—基本风压,N/m(基本风压为350)。
垂直于建筑物表面上的不同高度区域风载荷标准值计算结果如表2:
(1)第一排迎风面各节点风载

表2 不同高度区域风载荷标准值计算结果
由于风载荷标准值随着高度的变化而变化,所以要计算在不同高度区域的受力节点的载荷值。

式中:Fi—第一排迎风面计算区域各节点的平均风载—可变载荷的分项系数,取值为1.4;H—计算区域的高度,m;L—立体库的总长度,m;N—不同计算区域的节点总数。第一排迎风面不同高度计算区域各节点的平均风载计算结果如表3:

表3 第一排迎风面不同高度计算区域各节点的平均风载计算结果
(2)第一列迎风面各节点风载
当离地面的高度低于10m时:

式中:Fi—第一列迎风面计算区域各节点的平均风载,N, (i=7、8、9、10 );γQ—可变载荷的分项系数,取值为1.4;H—计算区域的高度,m;K—立体库的宽度,m;N—不同计算区域的节点总数。
第一列迎风面不同高度计算区域各节点的平均风载计算结果如表4:

表4 第一列迎风面不同高度计算区域各节点的平均风载计算结果
3.2 雪载计算
立体仓库所在地区冬季下雪较多,积雪会对屋顶施加压力,所以在计算时需要考虑雪载因素,雪载是作用在立体库顶端的载荷,由于仓库遮板与各货架在顶端节点连接,所以在加等效载荷时只需要加在各货架的顶端节点上。
根据立体仓库所放置的地理位置确定基本雪压为0.25kN/m2,顶端各节点的平均雪载[2]:

式中:F11—顶端各节点的平均屋面雪载,N;γQ—可变载荷的分项系数,取值为1.4;L—立体库的总长度,m;K—立体库的侧面宽度,m;J—屋顶载荷系数,N/m2;N—货架顶端节点数(480个)。
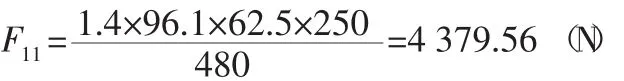
3 .3 地震载荷
根据我国主要城镇抗震设防烈度、实际基本地震加速度和设计地震分组查得设计地区为Ⅱ类场地、设计地震第一组,设计特征周期为0.36s[5],设计地区地震基本烈度为8度,设计基本地震加速度值为0.20g,所以货架地震载荷为0.20mg。
4 基于ANSYS的单排货架偏移结果分析
(1)立体库货架钢结构载荷
在货架结构设计中,货架的变形问题尤为重要[1],即较严格的精度问题。按照《建筑结构荷载规范》要求,立体仓库货架钢结构所承受的载荷分为两类:一类为永久载荷,只有结构自重;另一类为可变载荷,包括货物载荷、风载、雪载及地震载荷等[2]。由于该货架是框架结构,载荷效应组合可采用简化规则,并应按下列组合值中取最不利值确定:

式中:S—最不利载荷效应值;γG—永久载荷的分项系数[6],取值为1.2;γQ—可变载荷的分项系数,取值为1.4;SGK—按永久载荷标准值计算的载荷效应值;SQK—按可变载荷标准值计算的载荷效应值。
(2) ANSYS模型建立
由于货架的连接处和集中力处需要设置节点,而且节点的分布规则不均,故使用ANSYS的APDL模块(钢结构货架模块)对货架建立有限元模型,为了计算方便,建模时只对单排高密度货架以及仓库的连接最高点货架结构进行了建模,模型如图5为X-Z面建模,图7为Y-Z面建模。

图5 X-Z面建模

图6 X-Z面仿真结果

图7 Y-Z面建模

图8 Y-Z面仿真结果
(3)偏移仿真结果分析
在计算偏移时,货架钢结构受货物载荷、结构自重、风载、雪载以及地震载荷等的作用,按组合载荷来施加载荷,约束货架底端节点的所有自由度。有限元仿真结果如图6、图8,对于X—Z面来说,最大偏移点出现在第10层高位置,偏移量为17.814mm,距离地面高度为19 810mm,同样在Y—Z面的相同位置,货架在承受所有载荷的共同作用时,偏移向Y方向约17.814mm。
钢结构的许用挠度如表5[7],表中L代表受弯构件的跨度,由于货架钢结构约束了货架底端所有节点的自由度,故把结构近似认为是一个悬臂梁[4],L取值为货架的高度21 500mm。按照最不利值计算L/1 000=21.5mm来判断。货架的最大偏移值19.704mm小于许用挠度21.5mm。由此可以确定货架钢结构的刚度满足要求。
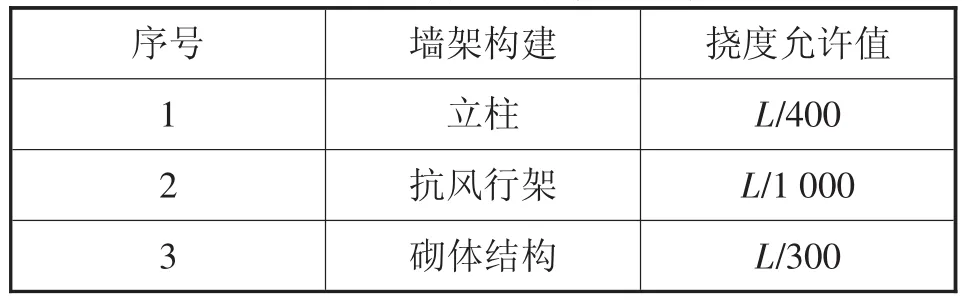
表5 钢结构设计挠度允许值
5 结论
本文简单阐述整体式立体仓库货架结构;并对货架结构进行静力分析、载荷分析与理论计算;通过ANSYS对单排高密度货架偏移结果进行仿真分析,得出该货架结构在正常工作载荷、风载、雪载和地震载荷等全载荷共同作用下,货架钢结构产生的偏移量未超出许用值,可以确定货架钢结构的刚度满足要求。

