基于优惠合同的在线租赁策略设计
徐维军, 董鹏翠, 彭子衿
(1.华南理工大学 工商管理学院,广东 广州 510641; 2.广州市金融服务创新与风险管理研究基地,广东 广州 510641)
0 引言
近年来,租赁以其集融资与融物于一体的特点吸引了越来越多的企业,租赁业己成为当今的“朝阳产业”。《2018上半年中国融资租赁业发展报告》显示,我国融资租赁企业数量、注册资金和业务总量一直在稳步增长。截至2018年6月底,全国融资租赁企业(不含单一项目公司、分公司、SPV公司和收购海外的公司)总数约为10,611家,较上年底的9,676家定比增长9.7%;全国融资租赁合同余额约为63,500亿元,较上年底的60,800亿元定比增长4.4%。随着租赁公司的数量以及业务量的快速增长,租赁公司之间的竞争也会越来越激烈,其中开展优惠活动是其增强自身竞争力的一种方式。因此当面对各种租赁选择时,承租人如何决策才能使得花费最少已成为了众多学者研究的内容。
在设备租赁活动中,出租方拥有设备的所有权,承租方只有在与出租方签订了包含双方权利及义务的合同后才能获得设备的使用权,因此许多学者在Karp[1]的基础上引进了“合同”因素[2]。Duan等[3]利用博弈论研究了两个有竞争力的二级运营商的投资和定价策略,根据收益阈值可以实现运营商投资和价格的均衡。Aurora等[4]介绍了承租方和出租方在识别、分类、确认和计量租赁合同时遇到的一些关键概念。考虑到合同内容的多样性,董玉成等[5]考虑了允许承租方退货的购买合同,研究了可退货在线租赁问题;王扬等[6]考虑了允许出租方回购的购买合同,以非线性指数价格函数为回购合同约束建立了在线租赁模型;杨兴雨等[7]分别研究了租赁合同约束下的单阶段和多阶段在线租赁问题,得到了最优在线租赁策略及其绩效比;徐寅峰等[8]研究了存在周期性折扣租赁合同时的最优在线策略;张桂清等[9]研究了以较优惠的价格租赁多个时间单位的租赁策略;肖鸣宇和沈正翔[10]研究了带有多折扣选项的滑雪租赁问题的最优离线和在线策略。现实生活中除了纯租赁和纯购买设备外,还有一些其他的方式,比如可以先付一定的购买金以减少之后的租金。为此,Lotker等[11,12]从随机算法的角度对不确定因素下的多选择策略进行了分析,给出随机算法下的在线策略及竞争比;Hu和Xu[13]改进了Lotker[12]等人给出的随机策略及竞争比;Fujiwara等[14]从确定性角度对该问题进行了分析,并给出了一个最优下界。
通常租赁公司的客户群体比较稳定,而且提供的产品可替代性较强,因此为了吸引更多的客户,租赁公司就会采取各种各样的营销策略。本文考虑了出租方想增加客户同时又不想损失太多利益、从而只为每个承租方提供一份优惠合同的情况,研究了存在优惠合同时承租人的在线租赁问题。
1 模型介绍与问题描述
在Karp提出的经典租雪橇问题中,承租方每期需要做出继续租用还是立即购买设备的决策。如果承租方是在设备需求期数已知的情况下做决策,则该承租方称为离线者,其面临的决策问题称为离线问题。如果承租方对设备未来需求期数未知则为在线者,在线者只有在每个租赁期开始时才知道是否继续使用设备,如需继续使用,可以选择租用或者购买设备,一旦购买则决策结束,这种决策问题称为在线问题。经典的租雪橇问题使用竞争比理论评价在线策略的优劣,从而得到最优在线策略。
竞争比理论的基本框架如下:将可供在线者选择的策略集记为Ω,离线者可输入的不确定序列集记为Φ。首先由在线者选择出一个在线策略A(A∈Ω),离线者会根据在线者的输出策略输入一个有限的序列I(I∈Φ),同时会在设备需求序列已知的情况下选出使得自己费用最小的策略,该策略即是最优离线策略。将在线策略A和最优离线策略的总费用分别记为CostA(I)和Costopt(I)。竞争比理论可以看作是在线者与离线者之间的博弈,在线者的目的是在未知离线者输入的情况下选出使得自己费用最小的在线策略A,离线者是在已知在线者选择的情况下输入使得策略A费用最大的设备需求序列。假设I是离线者的任一输入序列,如果存在一个与I无关的常数β使得CostA(I)≤β×Costopt(I)恒成立,则β的最小值称为在线策略A的竞争比。竞争比为β的在线策略可以保证对于离线者发出的任意输入序列,其费用不会超过最优离线策略费用的β倍。将策略集Ω中竞争比最小的策略称为最优在线策略,记为A*,其对应的竞争比即为最优竞争比。
本文在经典设备在线租赁研究的基础上,考虑了现实租赁市场中出租方为了吸引更多客户,从而为承租方提供了一份包含租赁期数和折扣信息的优惠合同情形。文中假设设备每期的租赁费用为1,购买费用为p(p>1)。优惠合同的内容为:承租方连续租用设备T期(T是整数),且在优惠合同期初付清所有的费用dT(d是租赁优惠折扣),若承租人在优惠合同期间停止使用,费用不予退回。
考虑到现实租赁活动中,由于承租方在优惠合约期限内违约无法获得补偿,优惠合同中的租期不宜太长,应小于某阈值,否则对客户的吸引力度不够。本文中设备的单位租金为1,购买价格为p,因此只有对设备的需求期数在区间(0,p)内承租方才会选择租赁,否则直接选择购买,为了便于分析,本文取其均值作为租期的阈值,即T
优惠合同的存在使得承租方在每期决策时多了一种选择,承租方在每期获取设备使用权时,需要考虑获取方式为单期租赁的普通合同、连续多期租赁的优惠合同还是购买合同。承租方对每台设备最多只有一次选择优惠合同的机会,一旦签订优惠合同,出租方不会对合同期内停止使用设备的承租方进行退款。本文研究的内容包括承租人是否会选择签订优惠合同,什么时候签订以及什么时候选择购买合同。
基于以上模型介绍以及问题描述可知,当存在一份优惠合同时,最优离线策略有以下结论:
定理1假设设备每期的租金为1,购买价格为p(p>1),优惠合同中的租期为T(T
(1)
接下来,将讨论不同情形下在线策略的费用,然后利用竞争比评价策略的优劣,从而选出最优在线策略和最优竞争比。
2 放弃优惠合同时的最优在线策略
当承租人放弃优惠机会,即选择不签订优惠合同时,可供选择的确定性策略记为A(t):在前t-1期一直选择单期租赁设备,到第t期如果仍需要设备则选择购买设备。在线策略A(t)的费用为:
(2)
其中,l是设备实际的需求期数。
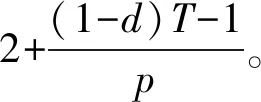
证明在线租赁问题中的需求期数由离线者决定,离线者是在已知在线者策略的情况下做出使得在线策略费用最多的选择,而在线者的目的是找出无论l取何值都能使得竞争比达到最小的t,记为t*。用l表示使用设备的实际期数,rt(l)表示在线策略A(t)的费用与最优离线策略费用的比值。根据在线算法可知,R(t)=maxlrt(l)表示在线者对输入的需求期数未知时确定性策略A(t)的竞争比,所对应的l值为离线者选择的输入序列;R*=minimaxlrt(l)表示在线策略的最优竞争比,对应的t值记为t*,则A(t*)是最优在线策略。下面将对t分情况讨论,从而找出t*以及最优竞争比:
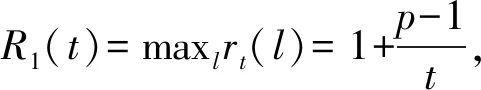
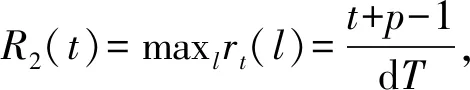
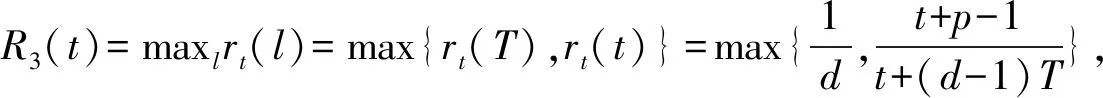
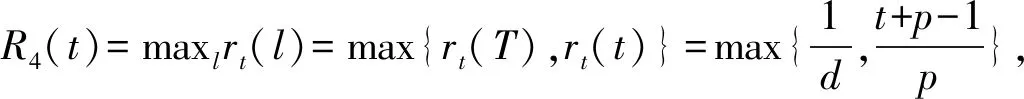

表1 不同情形下rt(l)的值及关于l的单调性
综上所述,放弃优惠机会时的最优竞争比为:
R(t*)=min{R1(t),R2(t),R3(t),R4(t)}

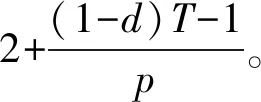
3 选择签订优惠合同时的最优在线策略
如果承租人不放弃优惠机会,则可供选择的确定性策略记为S(t1,t2):在前t1-1期一直选择单期租赁设备,到第t1期如果仍需要设备则选择签订优惠合同,到t2期仍需要设备则选择购买设备,其中t2≥t1+T。在线策略S(t1,t2)的费用为:
(3)
引理假设f(x)是某个区间[a,b)内的连续函数,c是一个常数,则在该区间内有minxmax{f(x),c}=max{minxf(x),c}成立。
证明若对于任意的x∈[a,b)都有f(x)≥c,则有下面的式子成立: 左边=minxmax{f(x),c}=maxxf(x)=max{minxf(x),c}=右边。
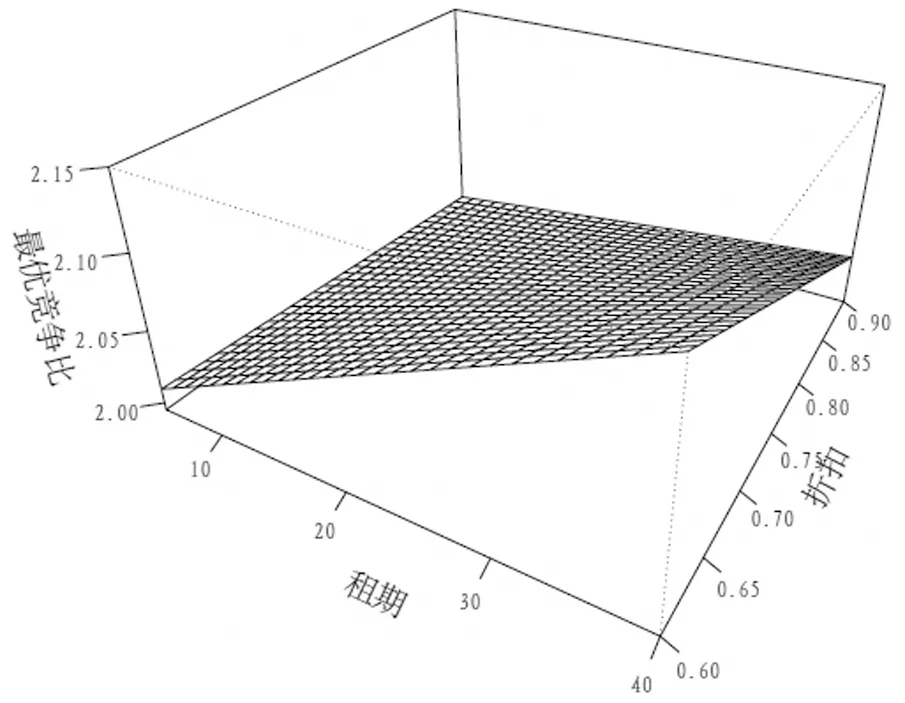
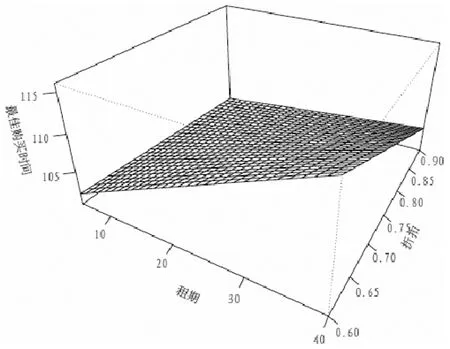
若存在一个x0∈[a,b)使得f(x0) 相应地,左边=minxmax{f(x),c}=c=max{minxf(x),c}=右边。因此引理成立。 证明在线策略S(t1,t2)的费用与最优离线策略费用的比值rt1,t2(l)可由公式(1)和公式(3)得到,接下来通过对t1分情况来讨论竞争比。 情形1当1≤t1 情形1-1当t1+T≤t2≤p+(1-d)T时,由公式(1)和公式(3)可得在线费用与最优离线费用的比值以及单调性如表2情形1-1所示。从单调性的分析中可以得到: =max{rt1,t2(t1),rt1,t2(t2)} 接下来在1≤t1 mint1,t2R11(t1,t2)=mint1,t2R11(t1,t2=p+(1-d)T) >R11(t1=dT,t2=p+(1-d)T) 情形1-2当t2>p+(1-d)T时,在线费用与最优离线费用的比值以及单调性如表2情形1-2所示。从单调性的分析中可以得到: =max{rt1,t2(t1),rt1,t2(t2)} mint1,t2R12(t1,t2)>R12(t1=dT,t2=p+(1-d)T) 综合情形1-1和情形1-2的分析可得,当1≤t1 R1=min{mint1,t2R11(t1,t2), (4) 情形2当dT≤t1 情形2-1当t1+T≤t2≤p+(1-d)T时,在线费用与最优离线费用的比值以及单调性如表2 情形2-1所示。从单调性的分析中可以得到: =max{rt1,t2(t1),rt1,t2(t2)} mint1,t2R21(rt1,t2)=mint1,t2R21(t1,t2=p+(1-d)T) =R21(t1=dT,t2=p+(1-d)T) 情形2-2当t2>p+(1-d)T时,在线费用与最优离线费用的比值以及单调性如表2情形2-2所示。从单调性的分析中可以得到: mint1,t2R22(rt1,t2)>R22(t1=dT,t2=p+(1-d)T) 综合情形2-1和情形2-2的分析可得,当dT≤t1 R2=min{mint1,t2,R21(t1,t2), (5) 情形3当T≤t1 情形3-1当t1+T≤t2≤p+(1-d)T时,在线费用与最优离线费用的比值以及单调性如表2情形3-1所示。从单调性的分析中可以得到: R31(t1,t2)=max{rt1,t2(tT),rt1,t2(t1),rt1,t2(t2)} mint1,t2R31(rt1,t2) >R31(t1=p-dT,t2=p+(1-d)T) 情形3-2当t2>p+(1-d)T时,在线费用与最优离线费用的比值以及单调性如表2情形3-2所示。从单调性的分析中可以得到: R32(t1,t2)=max{rt1,t2(tT),rt1,t2(t1),rt1,t2(t2)} mint1,t2R32(t1,t2)>>R32(t1=p-dT,t2=p+(1-d)T) 综合情形3-1和情形3-2的分析可得,当T≤t1 R3=min{mint1,t2R31(t1,t2),mint1,t2R32(t1,t2)} (6) 情形4当p-dT≤t1 R41(t1,t2)=max{rt1,t2(tT),rt1,t2(t1),rt1,t2(t2)} R4=mint1,t2R41(t1,t2)=mint1R41(t1,t2=t1+T) R4≥mint1max{f(t1),g(t1)} ≥max{f(p+(1-d)T),g(p-dT)} (7) 情形5当t1≥p+(1-d)T时,t2≥t1+T恒成立,在线费用与最优离线费用的比值以及单调性如表2情形5所示。从单调性的分析中可以得到: R5=mint1,t2R51(t1,t2)=mint1R51(t1,t2=t1+T) =R51(t1=p+(1-d)T,t2=t1+T) (8) 从定理3中可看到,选择签订优惠合同时的最优竞争比与不存在合同时的最优竞争比是相等的,该值只与设备的价格有关,与优惠合同内容无关。然而这并不能说明关于优惠合同存在的研究是无意义的,因为两种情况下的最优离线费用是不相等的,不存在优惠合同时的最优离线费用一定大于优惠合同存在时的最优离线费用。因此对于承租者来说,虽然竞争比一样,但其最终支付的费用是小于合同不存在情况的。除此之外,定理3还给出了选择签订优惠合同时的最佳签订合同时间、最佳购买设备时间与合同中租期、折扣之间的函数关系,这为承租者的决策提供了理论依据。 表2 不同情形下rt1,t2(l)的值及关于l的单调性 汽车融资租赁是指出租人根据承租人对汽车和供货人的选择,将其从供货人处取得的汽车按照合同约定出租给承租人并收取租金的经济活动。中国的汽车租赁租赁市场于2008 年起步,目前处于成长初期。有数据显示,我国汽车金融的渗透率约为25%,其中融资租赁的比例只有2%不到,然而在美国等发达国家汽车金融的渗透率高达80%,其中融资租赁占比超过40%。融资租赁是一种强有力的促销手段,未来在中国汽车市场将会迎来快速的发展。汽车融资租赁企业想要增强自身的竞争力,需要不断拓展业务以及加强模式创新,从而为承租方提供更多的选择。面对选择时如何做出最优决策对承租人来说意义重大。 假设某汽车融资租赁企业的某种设备每期的租赁费用为1,购买价格p为100,企业提供的租赁优惠合同中的租期为T,折扣为d。由定理3可知当承租人选择签订优惠合同时的最优竞争比与合同内容无关,仅与设备的购买价格有关,为1.99。图1显示了承租人放弃优惠机会时的最优竞争比随合同中租期和折扣的变化而变化的情况。从图中可以看出,最优竞争恒大于2,且随着合同中租期的增加或者折扣的减少而增大。对比两种情形下的最优竞争比可看出,对承租者来说当存在优惠合同时,选择签订优惠合同是较优的策略。 图1 不放弃优惠合同时最优竞争比与合同中的租期、折扣的关系图(P=100) 图2 最佳签订优惠合同时间与合同中的 租期、折扣的关系图(P=100) 当承租人选择签订优惠合同时,接下来对汽车承租人最佳签订优惠合同时间和最佳购买设备时间进行数值分析。图2显示了最佳签订优惠合同时间随着合同中租期和折扣的变化而变化的情况,从图中可以看出,最佳签订优惠合同时间随着合同中连续租赁期数的增加而推迟,随着合同中优惠力度的增加而推迟。图3显示了最佳购买设备时间随着合同中租期和折扣的变化而变化的情况,最佳购买设备时间随着合同中连续租赁期数的增加而推迟,随着合同中优惠力度的增加而推迟。 图3 最佳购买设备时间与合同中的 租期、折扣的关系图(P=100) 针对设备租赁市场竞争日益激烈的现状,本文基于经典的Karp租雪橇在线竞争比模型,研究了存在一份优惠合同时承租者的在线决策问题。当存在优惠合同时,承租者有权利选择是否签订该合同,因此本文研究了放弃合同和签订合同两种情形下的最优在线策略以及最优竞争比,同时得到了签订合同情形下的最佳签订合同时间和最佳购买设备时间。最后通过汽车租赁的数值算例说明,当存在优惠合同时选择签订合同是更好的选择,签订合同的最佳时间随着合同中租期或者折扣的增加而推迟,最佳购买时间随着合同中租期的增加而推迟、随着折扣的增大而提前。现实租赁市场中,出租方提供的优惠活动形式是多种多样的,除了优惠合同外,影响承租方决策的因素还有通货膨胀、利率以及承租方的风险偏好等,不同影响因素下承租方的在线决策问题都可以使用在线算法和竞争比理论进行研究。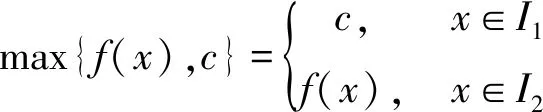

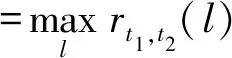
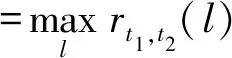
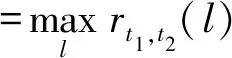

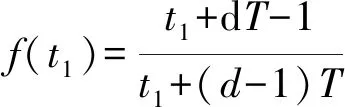
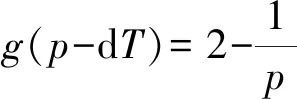


4 数值分析

5 结论

