突扩式消力池R型水跃的长度特征分析
傅铭焕,梁维军,陈炳斌,洪银有,卢志男,张志昌
(1.浙江省水利水电勘测设计院,浙江 杭州 310002;2.浙江铭诚建设有限公司,浙江 绍兴 312030;3.西安理工大学,陕西 西安 710048)
1 研究背景
自贝登(G.Bidone)1818年研究水跃现象以来,距今约有200年的历史。水跃共轭水深关系作为水跃控制的重要参数,备受各家学者关注。但表征水跃特性的另一重要参数——水跃长度,却由于水流的复杂性,其研究成果远没有共轭水深研究的深入与透彻。现阶段水跃长度的研究成果多为各家学者提出的经验或半经验公式,关于水跃长度的理论研究还相对较少。
Rajaratnm[1]和Hughes[2]先后将水跃分为水跃旋滚长度Lr和水跃长度Lj,其中水跃旋滚长度是指水跃跃首断面到水跃表面旋滚末端断面之间的水平距离,而水跃长度是水跃跃首至跃后水深约等于尾水水深时两断面间的水平距离。文献[3]收集了国内外43个水跃长度公式,按其跃后水深、跃前和跃后水深、跃前断面的弗劳德数与跃前或跃后水深以及其他表示方法进行了分类,并明确了水跃长度与旋滚长度的关系。
突扩式消力池作为一种特殊消能工,常被布置于上下游渠道断面宽度不一致的河床上,用以衔接上下游水流。发生于突扩式消力池内的水跃称为突扩式水跃。突扩式水跃有别于一般二元水跃,是一种三元水跃。文献[4]和文献[5]根据突扩式水跃跃首断面位置的不同,将其分为R型、S型和T型共3种水跃。
文献[4]-[9]研究了S型水跃水跃区沿程断面流速分布、水跃跃后水深、水跃长度及消能率的变化规律。其中文献[9]通过建立水跃区水体质点的运动方程,研究突扩式消力池水跃跃长的变化规律,提出了突扩式消力池S型水跃跃长的半理论公式。
文献[4]试验研究了R型水跃跃后水深和水跃旋滚长度、水跃长度的变化规律。研究表明,R型水跃旋滚长度随着扩散出流断面弗劳德数的增大而增大,但由于旋滚长度变化的复杂性,其并未给出具体的计算公式。
由以上研究可以看出,突扩式消力池R型水跃的研究成果较少,虽有学者对其变化规律做了定性分析,但并未提出定量计算公式。作者旨在重新分析文献[4]的试验成果,得出R型水跃各特征长度的定量关系,为R型水跃突扩式消力池设计提供参考。
2 R型水跃参数
图1为一突扩式消力池R型水跃简图。由图1可知,下泄急流从较窄渠道突然出流扩散到较宽渠道时,主流沿渠道前进方向有一滑行段,该滑行段水流断面水深沿程逐渐减小,即断面水深从出流时的h0降到水跃跃前断面水深h1,此时主流滑行的水平距离为L1。由于下游水深的顶托作用,下泄主流在较宽渠道内发生水跃,断面水深相应从h1发展到跃后断面水深h2,此时主流旋滚段长度为Lr。由于衔接渠道断面的突然扩大,水流会在断面突然扩大处附近形成部分回流,回流段水平长度L0见图 1。图中,b 为上游渠道宽度,B 为下游渠道宽度,v0、v1、v2分别为扩散出口断面、跃前和跃后断面的平均流速,ω为水流扩散角。

图1 突扩式消力池R型水跃简图
3 回流段长度与水流扩散角
当消力池边墙沿程向两侧扩散时,下泄水流就有可能扩散不佳,致使边壁处产生回流。文献[10]的试验结果表明当边墙扩散角为9°时,水流出现脱壁现象,在边壁处有回流产生。文献[4]试验结果亦表明,突扩式消力池中(边墙扩散角为90°),下泄水流流经突然扩大断面时,水流会向两侧边墙扩散并形成回流。文献[4]给出了回流段水平长度L0的计算公式,即:

式中,Fr0为扩散出口断面弗劳德数,2.21<Fr0=v0/h0<8.88;g为水流重力加速度。
由公式(1)可知,回流段水平长度L0是扩散出口断面弗劳德数Fr0和消力池上下游断面宽度差B-b的函数。笔者根据文献[4]的试验数据,对公式(1)的计算结果进行了验证。结果表明,公式(1)计算的R型水跃回流段水平长度L0的平均误差为4.62%,最大误差为16.17%。
对公式(1)进行变形可得水流扩散角ω的计算式,即:
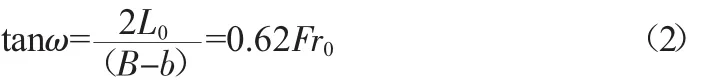
由公式(2)可知,水流扩散角ω是Fr0的函数,并随着Fr0的增大而增大。
文献[11]亦试验研究了突扩式水跃水流扩散角ω的变化规律,提出的水流扩散角ω的计算公式为:

由公式(2)和公式(3)比较可知,文献[4]和文献[11]均认为水流扩散角ω为水流扩散出口断面弗劳德数的函数,但公式(3)的系数略大于公式(2)的系数。分析认为,这是由于突扩式水跃在回流段紊动强烈,使施测者施测困难造成的。由于公式(3)并未给出具体的试验突扩比及扩散出口断面弗劳德数的变化范围,故笔者建议使用公式(2)计算水流扩散角ω和回流段水平长度L0。
4 射流距离
同S型和T型水跃不同,R型水跃由于下游尾水水深相对较浅,下泄水流在流经扩散出口断面后仍有一段急流滑行。在该滑行段内,水流断面水深沿程逐渐减小,直到水跃跃前断面平均水深,后水流发生水跃现象。此时主流滑行段的水平距离为L1(下文称射流距离)。
文献[4]分析了相对射流距离L1/(B-b)随Fr0的变化规律,但其并未给出射流距离L1的具体计算公式。笔者重新整理分析文献[4]的实测资料,得到射流距离L1新的变化规律如图2所示。(文献[4]试验的消力池突扩比β=B/b分别为1.2、1.5、2、3和6共5种体形。由于文献[4]在β=6时的试验工况只有2组,且其与其余4种体形的突扩比变化跨度较大。为了更好的分析射流距离的变化规律,本文图2中并未将只有2组工况的β=6体形列入讨论。)
由图 2可知,在突扩比 β=1.2~3,2.21<Fr0<8.88情况下,突扩式消力池R型水跃的相对射流长度L1/(B-b)与Fr0/β0.2近似呈线性分布,相对射流长度L1/(B-b)随Fr0/β0.2的增大而增大。对图2进行拟合可得射流长度L1的计算公式为:
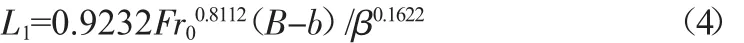
公式(4)计算的最大误差为17.72%,平均误差为6.77%,在43组工况中,只有11组的计算误差超过10%。可见公式(4)具有较高的计算精度。公式(4)的适用条件为突扩比,β=1.2~3,2.21<Fr0<8.88。
用公式(4)检验突扩比β=6时的2组试验工况,计算的射流距离L1分别为61.61 cm和74.19 cm,与实际值71.12 cm和91.44 cm的误差分别为-13.38%和-18.87%。由此可知,公式(4)虽由突扩比β=1.2~3的试验工况得出,但其计算的大突扩比射流距离并未产生明显的偏离,其对大突扩比R型水跃的适用性后续可进一步验证。
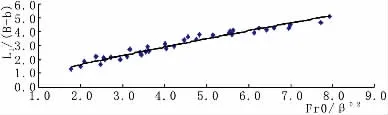
图2 射流距离的变化规律
5 水跃旋滚长度
由图1可知,突扩式消力池R型水跃有别于S型水跃和T型水跃,其跃前断面明显远离扩散出口断面,R型水跃的整个水跃旋滚段位于扩散后的渠道内。但同一般二元水跃不同,R型水跃回流末端后由于水流反射、冲击波等影响,R型水跃跃前断面在两侧边墙附近仍会受到额外的紊动作用力。
1990年,Hager[12]等给出了水跃旋滚长度的公式为:

式中,跃前断面弗劳德数Fr1=2.5~8。
本文忽略R型水跃回流末端后水流的反射、冲击波作用,根据文献[4]的试验工况并结合公式(5)探讨突扩式消力池R型水跃旋滚长度计算的可行性。
文献[3]收录了43个计算水跃长度和水跃旋滚长度公式,并对其进行了分析。分析结果表明,美国垦务局[13]给出的水跃长度公式,即Lj=6.1h2计算的水跃长度比较准确。文献[3]通过分析,发现在弗劳德数为1.82~7.67时,水跃长度是水跃旋滚长度的1.973~1.614倍。
由上述结论可知,一般二元水跃的水跃旋滚长度约大于跃后水深的3倍。笔者分析文献[4]的水跃旋滚长度发现,其施测的部分水跃旋滚长度严重偏小。分析认为,这可能是由于突扩式消力池R型水跃的强烈紊动给施测者施测带来困难造成的。为了更好分析R型水跃旋滚长度的变化规律,同时考虑突扩式消力池R型水跃的特殊性,筛除旋滚长度与跃后水深之比小于2.5的试验工况,对文献[4]中的水跃旋滚长度重新进行分析。文献[4]的具体试验参数与实测结果详见表1。文献[4]试验研究的突扩比分别为1.2、1.5、2、3、6五种消力池体形共45组工况,筛除旋滚长度与跃后水深之比小于2.5及突扩比为6时的2组工况后剩余37组工况。本文用扩散断面弗劳德数代替跃前断面弗劳德数,用公式(5)反算得到的跃前断面水深h1见表1。同时,表中还列出了衰减系数ζ=h1/h0的实测值。

图3 衰减系数ζ的变化规律
笔者对衰减系数ζ进行分析,分析结果见图3。由图3可知,衰减系数ζ是消力池突扩比、跃后断面水深与扩散断面水深之比的函数。对其拟合可得:

另跃后断面水深与扩散断面水深之比为η',则公式(6)变形为:

公式(7)计算的衰减系数ζ值见表1。根据公式(7),即可求得R型水跃跃前断面水深h1为:

将公式(8)带入公式(5),可得R型水跃旋滚长度的计算公式为:

由公式(9)可知,R型水跃旋滚长度随Fr0和h0的增大而增大,随β和η'的增大而减小。由于公式(9)在推导过程中忽略了R型水跃回流末端后水流反射、冲击波等的影响,并且用扩散出流断面Fr0代替原公式(5)中的跃前断面弗劳德数Fr1。故公式(9)计算的R型水跃旋滚长度需进行修正。另修正系数为公式(9)计算值 Lr'与文献[4]实测值 Lr[4]的比值,即 ξ=Lr'/Lr[4]。用文献[4]上下游资料计算的修正系数ξ见图4,对图4进行拟合可得:


图4 修正系数的变化规律
故修正后的突扩式消力池R型水跃旋滚长度,即:
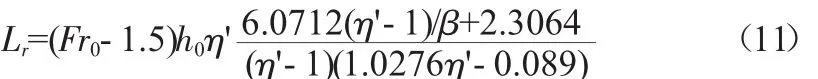
公式(11)的适用条件为突扩比 β=1.2~3,2.21<Fr0<8.88。

表1 文献[4]试验参数表
公式(11)计算的37组R型水跃旋滚长度只有一组误差超过20%,最大误差为20.37%,平均误差为10.25%,计算结果见表1。表1中还列出了用公式(11)计算的另6组(即6组旋滚长度与跃后水深之比小于2.5的工况)试验工况值计算值,43组R型水跃旋滚长度的平均误差为14.46%。由此可知,根据公式(5)探讨突扩式消力池R型水跃旋滚长度计算的可行性。
6 结语
本文通过文献[4]的实测资料,分析与研究了突扩式消力池R型水跃主要特征长度——回流扩散段水平长度、射流长度及旋滚长度的变化规律。研究发现,R型水跃边墙扩散角是出流断面弗劳德数的函数,文献[4]提出的回流扩散段水平长度公式具有较好的计算精度。相对射流长度L1(B-b)随Fr0/β0.2的增大而增大,笔者提出的射流长度公式计算的平均误差为6.77%。定义了表征跃前断面水深和扩散出流断面水深关系的衰减系数概念,分析发现衰减系数ζ是消力池突扩比、跃后断面水深与扩散断面水深之比的函数。给出了R型水跃旋滚长度的计算公式,该公式计算的平均误差为10.25%。

