基于图像重建的CT系统参数标定与成像模型

万 犇，贾昀达，王宏晔，张 勇

(1.电子科技大学 数学科学学院，四川 成都 611731；2.电子科技大学 自动化工程学院，四川 成都 611731)

典型的二维CT系统是由探测器、待重建物体和X射线组成，平行入射的X射线垂直于探测器平面，每个探测器单元看成一个接收点，且等距排列。

X射线的发射器和探测器相对位置固定不变，整个发射-接收系统绕某固定的旋转中心逆时针旋180次。对每一个X射线方向，在具有512个等距单元的探测器上测量经位置固定不动的二维待检测介质吸收衰减后的射线能量，并经过增益等处理后得到180组接受信息。

为了确定CT系统旋转中心在正方形托盘中的位置、探测器单元之间的距离以及该CT系统使用的X射线的180个方向，在正方形托盘上放置固体介质组成的标定模板，模板的几何信息可用一个256维的方阵来表示，其中每一点的数值反映了该点的吸收强度，本文中称为“吸收率”。对应于该模板的接收信息可用一个180维的向量来表示。利用这一模板及其接收信息，可对CT系统进行参数标定。

利用得到的标定参数和某未知介质的接收信息，可确定该未知介质在正方形托盘中的位置、几何形状和吸收率等信息。

1 建模前准备

根据CT系统的工作原理[1]，得到如图1所示的CT系统示意图。为了标定CT系统的参数，这里采用的标定模版由两个均匀固体介质组成，在二维平面上分别是一个椭圆和圆，具体的介质形状和参数如图2所示。

图1 CT系统示意图

图2 模板示意图(单位：mm)

在建立模型之前，先对已有数据进行处理和观察，以简化相应的物理机理，从而降低模型建立的难度。

1.1 CT系统旋转过程的大致确定

根据标定模版的吸收率方阵[2]，画出标定模版的形状，如图3所示，利用标定模版得到180组探测器接收信息，三维图如图4所示。

图3 依标定模板吸收率方阵画的标定模版示意图

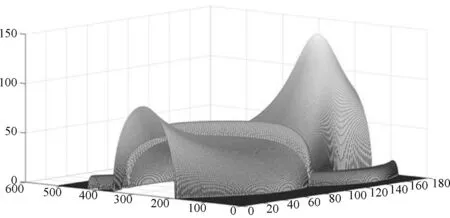
图4 180组探测器接收信息三维图

从图4得到，探测器接收信息的值有高有低，且经过椭圆圆心附近的X射线对应的探测器的值在同一组值中最高，说明探测器接收信息的值与X射线穿透物体的长度成正相关。

利用上述原理，可得到X射线方向经由垂直于椭圆长轴到垂直于椭圆短轴，又由于CT系统是逆时针旋转的，所以可以得到如图5所示的CT系统旋转过程。

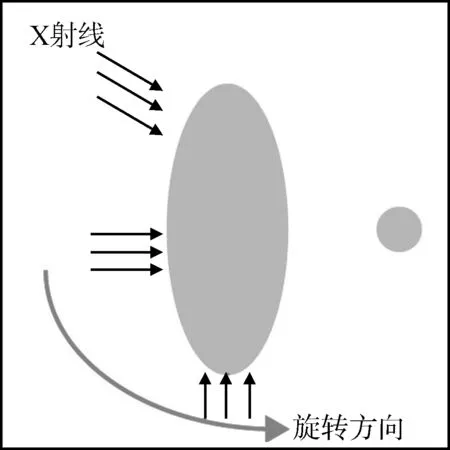
图5 CT系统旋转过程

1.2 三个近似处理

从图4容易看出，圆所对应的探测器值的变化。根据圆所对应的探测器的变化规律，得到CT系统旋转了180°左右，每次旋转在1°左右。由于偏转角度只有1°左右的误差以及探测器之间的间距较小，所以所有的探测器值中有最高值的那组可认为是X射线的方向垂直于模板中椭圆的短轴，如图6所示。

图6 方向垂直椭圆短轴

图7 方向垂直椭圆长轴

当X射线垂直于椭圆长轴时，除去圆对应的探测器，由于经过椭圆圆心的弦长轴最长，原则上，此时探测器不为0的个数是最多的，所以椭圆对应的探测器不为0的个数最多的时候大概是X射线方向垂直于椭圆长轴的时候，如图7所示。

不考虑模板中圆对探测器值的贡献，对于每一个方向下的探测器接收到的值都有一个最大值，根据平行线经过椭圆原点的弦弦长最长的原理，可近似认为每一组探测器接受数值中最大值对应的X射线经过椭圆的圆心，如图8所示。

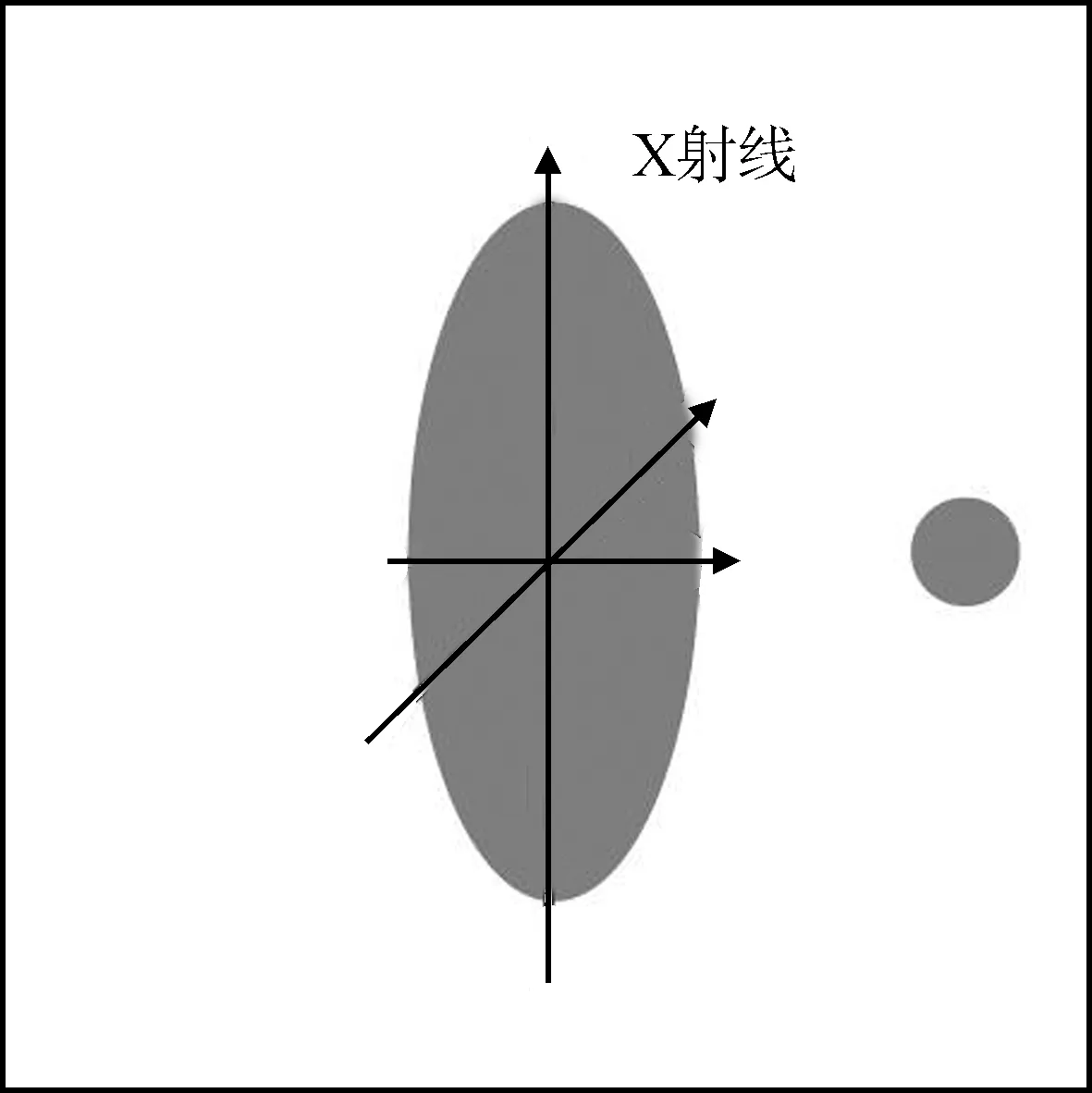
图8 经过椭圆圆心的X射线

由此建立CT系统参数标定和成像模型前，做了如下3个近似处理[3]。

1)所有的探测器值中有最高值的那组为X射线的方向垂直于模板中椭圆的短轴情形下测得。

2)椭圆对应的探测器不为0的个数最多的时候为X射线方向垂直于椭圆长轴。

3)每一组接收信息中，探测器的值最高的对应的X射线经过模板中椭圆的圆心。

1.3 消除圆对探测值的影响

根据图4，有可能会因为圆和椭圆两段长度的叠加，导致每一组最大值对应的X射线并不穿过椭圆的圆心，为了能够让最大值对应的X射线穿过椭圆圆心，必须消除圆对探测值的影响，所以可以采取滤波的方式对其进行处理。

首先分析圆平均会影响多少个探测器的值，每个探测器影响的值大概是多少，然后对每一组数据进行梯度检测，如果相应数据产生的梯度(或者二阶差分值)满足一定的条件，就减去圆对探测器所产生的影响。下文所有提到探测值都是指滤波之后的探测值。

2 CT系统参数标定模型的建立

探测器单元之间的间距可利用某一段实际长度与对应的探测器单元个数求解得到，CT旋转中心和X射线180次方向可基于建立的直角坐标系，经机理分析得到的相应方程求解得到。

2.1 确定探测器单元之间的间距

如果知道多个探测器单元的总长度以及对应的探测器单元的个数，就可以确定探测器单元之间的间距。而对于实际长度，只知道模版以及正方形托盘的相应参数。

首先找到X射线垂直于椭圆直径透射时探测器的值。由之前的近似处理，椭圆对应的探测器不为0的个数最多的时候为X射线方向垂直于椭圆长轴，所以椭圆对应的探测器不为0的个数最多的时候就是X射线垂直于椭圆直径透射的时候。

然后将椭圆的长轴长度作为实际长度，若要计算探测器单元之间的间距，就要知道此椭圆长轴对应的探测器单元个数N，但是此时只能知道探测器值不为0的探测器单元个数Nl。Nl的求解只需要知道第一个不为0的探测器编号和最后一个不为0的探测器编号，对于第一个不为0的探测器编号由如下优化模型确定：

min i

s.t.Rli≠0

其中，Rli表示第l次第i个探测器对应的值。对于最后一个不为0的探测器编号由如下优化模型确定：

max j

s.t.Rli≠0

假设上述问题求解结果为i0和j0，则Nl=j0-i0+1。

此时Nl个探测器单元之间的长度是小于椭圆长轴长度的，但是Nl个探测器单元对应的探测器长度比它们之间的长度之和多出一个探测器单元间距d，而且探测器单元之间的间距较小，所以可直接将椭圆长轴对应于Nl个探测器单元，由此可求解出探测器单元之间的间距：

(1)

式中，b为椭圆长半轴的长度。

2.2 确定CT系统的旋转中心在正方形托盘的位置

若要确定旋转中心，一定要有两个方向，再建立直角坐标系，通过中心旋转的相关知识，设出未知量和参数，联立方程，最后求解可得到CT系统的旋转中心。

首先不妨选取X射线垂直于椭圆长轴和垂直于椭圆短轴时的两种特殊情况。之前已经得到X射线垂直于椭圆长轴透射时的情形，所以只需要得到X射线垂直于椭圆短轴透射时的情形。由探测器的探测值最大所对应的那组数据即为X射线垂直于椭圆短轴透射时的接收信息，即：

max Rij

其中，Rij为X射线垂直椭圆长轴时第j个探测器的值。求解得到的i0对应的Ri0为X射线垂直于椭圆短轴透射时的接收信息。

此时还可以得到两组数据中各自的最大值Rlm和Rsm，对应着的X射线分别与椭圆短轴和长轴重合，分别对应的探测器编号为m与n。

然后以椭圆圆心为圆心，短轴为x轴方向，长轴为y轴方向建立直角坐标系，如图9所示。

图9 求解旋转中心示意图

X射线垂直于椭圆长轴透射时，此时第m个探测器正对于x轴，纵坐标为0，设横坐标为x0；X射线垂直于椭圆短轴透射时，此时第n个探测器正对于y轴，横坐标为0，设纵坐标为y0。

将两次旋转中，对应的探测器单元连接，得到一系列线段。根据中心旋转的原理，这些线段的中垂线将相交于一点，该点就是旋转中心。如图9所示，为方便起见，将X射线垂直于椭圆长轴透射时，从上到下的探测器坐标分别设为(x0,0)、(x0,y1)、(x0,y2)和(x0,y3)。将X射线垂直于椭圆短轴透射时，从左到右的探测器坐标分别设为(x1,y0)、(x2,y0)、(x3,y0)和(0,y0)。

对于第m个探测器，两点连线的斜率为y0/(x1-x0)，所以其中垂线的斜率为(x0-x1)/y0。中垂线还经过两点的中点((x0+x1)/2,y0/2)，所以可以得到对应的中垂线方程：

(2)

同理，可以得到其他3条中垂线方程：

(3)

(4)

(5)

式中，x1=-k1d，x2=-k2d，x3=-k3d，y1=-k3d，y2=-k2d，y3=-k1d,0

将式(2)～式(5)进行联立，可得一个方程组：

(6)

求解方程组(6)，得到(x，y)、(x0，y0)，其中(x,y)即为CT系统旋转中心在坐标系中的坐标，即可确定在正方形托盘中的位置。

2.3 确定X射线的180个位置

由于最大值与透射的长度有关，所以先应用数值拟合得到Rim与对应的透射长度lim的关系，再利用解析几何知识得到投射长度lim与X射线的旋转角度θi关系，从而求解出X射线的180个方向。

2.3.1 数值拟合求探测值和透射长度的关系

不妨假设探测值与透射长度之间存在线性关系，可利用数值拟合求探测值和透射长度之间的线性关系，先求出回归函数的参数，再做出图像，分析残差值，如果残差值较小，则探测值与透射长度之间存在线性关系，并且求得探测值与透射长度的解析表达式。

对着多组数据进行拟合，不妨设拟合函数R=al+b，拟合函数中a、b使得残差平方和最小，即：

利用最小二乘法[4-5]求解上述优化问题，即对a、b求偏导，令其等于0，得到：

(7)

求解方程组(7)，可得到每组探测值中的最大值Rim与穿透长度lsi的线性关系：

Rim=alsi+b

(8)

2.3.2 基于解析几何求解X射线的180个方向

本文为方便起见，X射线的方向θi定义为X射线方向与x轴正方向之间的夹角。首先通过解析几何知识推导出X射线的方向θi与透射长度lsi的关系。如图6所示，将

(9)

(10)

从而得到X射线方向的求解解析式：

(11)

式中，lsi为该组探测值中最大对应的透射长度。

利用处理后的探测值和式(8)、式(11)，可以计算出X射线的180个方向。

2.4 CT系统参数标定模型的求解结果

以正方形托盘左下角为原点建立直角坐标系，通过MATLAB求解得到，CT系统的旋转中心坐标为(59.543 1,43.778 7)，位于正方形托盘中心右偏下33.101 0゜，距离11.391 9 mm处；探测器单元间的距离为0.276 8 mm；X射线的180个方向是绕旋转中心从右偏下60.335 4゜,每次逆时针旋转大约1゜到左偏上61.347 9゜。

3 CT系统成像模型的建立

首先基于傅立叶切片定理利用滤波反投射方法得到原来二维物体的图像，利用灰度表示为矩阵。由于探测器单元的间隔大于正方形托盘上离散点间的距离，所以得到的矩阵维数是大于所求的矩阵维数，需对矩阵进行压缩。利用模版得到矩阵中值与吸收率之间的关系，从而求得二维物体的吸收率。

3.1 基于傅立叶切片定理的滤波反投射方法确定位置与形状

傅立叶切片定理[6]说明了由一维的图像信息可以恢复出二维的图像信息，具体过程如算法1。

算法1：滤波反投射方法[7]

1)计算每个投影的一维傅立叶变换；

2)用滤波函数|ω|乘以每个傅立叶变换；

3)得到步骤2导致的每个滤波后的变换的一维傅立叶反变换；

4)对步骤3得到的一维反变换求和，得到二维函数。

此时，由于旋转中心与正方形托盘中心并不重合，所以还需要对上述得到的图像与矩阵进行平移，然后就可以得到原来二维物体的位置和形状。

3.2 矩阵的压缩处理

由于探测器单元之间的间距为0.276 8 mm，而将正方形托盘离散化后，一共256×256个离散点，每个离散点之间的间距为0.39 mm，所以重建图像中的离散点之间的间隔也为0.276 8 mm，若要使重建图片与原图相同，则需要362×362个离散点，所以经滤波反投射方法得到的矩阵A为362维的，要转化为256维的，需要对矩阵进行降维。矩阵或者图像的压缩可直接使用MATLAB中的imresize函数[8-9]。

3.3 基于数值拟合确定吸收率

一个二维物体可以用一个吸收率矩阵X表示，该二维物体经过CT系统可以得到180组探测数据，同样也可以表示成一个矩阵R。矩阵R经过滤波反投射方法可以变为362维的矩阵A，经过矩阵压缩处理得到256维的矩阵Y，如图10所示。

图10 CT系统成像流程图

此时可以通过上述方法得到矩阵Y，由矩阵Y推算原来二维物体的吸收率矩阵X，所以现在需要寻找矩阵Y与矩阵X之间的关系，也就是X中每一个元素对应到Y是怎么变化的，只要求得矩阵X与矩阵Y之间的关系，即可确定原来物体的吸收率矩阵。

可以利用模板进行求解矩阵X与矩阵Y之间的关系，由于矩阵X中的元素值都为0或1，所以最后得到的矩阵Y应该也是两个常数，由于一些“噪声”的干扰，矩阵Y中的元素为在两个常数之间波动的一些数。主要探究的是矩阵X中值为1的元素经过上述一系列变换变为了多少，所以需要对矩阵Y进行预处理，将小于一定值的元素舍去，求剩下元素的期望，作为矩阵X中值为1的元素变换后的值。

矩阵X前乘上不同的系数，观察变换后的值的变化情况，利用数值拟合求解出两者之间的关系，从而可以通过矩阵Y得到吸收率矩阵X。具体过程如算法2。

算法2：基于数值拟合的确定吸收率算法

1)确定迭代倍数k，迭代次数i=1，终止条件n，以及已知吸收率0-1矩阵X。

2)如果i=n，停止迭代，转步骤4)；否则，Xi=kXi-1，xi=ki，其中xi为Xi中最大元素。将X经CT系统，滤波反投射和矩阵压缩得到对应的矩阵Yi。

3)找出矩阵Yi中最大元素max，舍去小于max/2的元素值，对剩下元素求平均得yi。转步骤2)。

4)分别对xi和对应值yi进行数值拟合，从而确定矩阵X与矩阵Y之间的关系。

如果矩阵X与矩阵Y之间是线性关系，则存在常数K，使得X=KY，从而可根据探测值矩阵推算出吸收率矩阵。

3.4 CT系统成像模型的求解结果

对于滤波反投射方法，可直接利用MATLAB中的iradon[10-12]函数，由于根据CT系统参数标定模型，求得CT系统的旋转中心在椭圆圆心(正方形托盘中心)右偏下33.101 0，距离11.391 9mm的地方，所以对iradon函数得到的图像进行平移，然后再依据X射线的旋转角度，可以得到对应的二维物体的位置和形状，根据文献[1]提供的附件3和附件5数据，两个未知介质的形状如图11和图12所示。

图11 文献[1]的附件3黑白形状图

图12 文献[1]的附件5黑白形状图

从图中可以看出，文献[1]中附件3的二维物体是一个“人脑”CT形状，位于正方形托盘的中心；文献[1]中附件5的二维图片是某个“生物组织”CT形状，位于正方形托盘的中心。

本文吸收率矩阵X选取标定模板的吸收率矩阵，分别用不同的系数xi乘上矩阵X，再经CT系统，滤波反投射和矩阵压缩得到图像矩阵Y，然后对矩阵Y中元素进行筛选和求期望，得yi，利用线性函数数值拟合xi和yi，得如图13所示图像。

图13 吸收率矩阵和图像矩阵线性拟合图像

从图13中可以看出，xi和yi几乎是呈线性关系的，也就是说吸收率矩阵X和图像矩阵Y呈线性关系为：

X=1.944Y

(12)

从而通过上述操作可以将接收器接收到的180组一维接收信息的数据转化成256维的吸收率矩阵。

4 结束语

本文由于近似处理，减小计算量的同时，也损失了精度；在求解CT系统的旋转中心时，由于初值对方程组的求解影响特别大，所以稳定性不高。但是本文所建立的模型对CT系统参数标定和成像都具有一定的指导意义。