高温作业专用服装设计的数学建模
陈天同 崔世宝 鲍骏


摘 要:在高温环境下进行工作具有极高的危险性,因此人们往往会在工作时穿上专用的热防护服以保证自身安全。高温环境下工作时的专用服装一般都是三层织物材料组成的。热防护服装是应用最为广泛的高温防护服装。目前关于热防护服装的设计集中在热防护性能的测定、建立热防护服装内部的传热模型以及发展测定热防护性能的试验方法等。研究的是在一定的环境温度下,身着热防护服的假人的皮肤温度变化的热传导模型。
关键词:热防护服 热传导微分方程 最优化模型 最优厚度 Matlab软件
中图分类号:O175.2;TS941 文献标识码:A 文章编号:1674-098X(2019)11(a)-0119-06
Abstract: It is very dangerous to work in high temperature environment, so people often wear special thermal protective clothing to ensure their own safety. The special clothing when working in high temperature environment is generally composed of three layers of fabric. Thermal protective clothing is the most widely used high temperature protective clothing. At present, the design of thermal protective clothing focuses on the measurement of thermal protection performance, the establishment of heat transfer model in thermal protective clothing and the development of test methods for measuring thermal protection performance. In this paper, the heat conduction model of skin temperature change of dummies dressed in thermal protective clothing at a certain ambient temperature is studied.
Key Words: Thermal protective clothing; Heat conduction differential equation; Optimal model; Optimal thickness; Matlab software
1 問题的重述
1.1 问题的背景
当人们的工作环境超过了人体舒适温度,就极容易发生危险。因此,在高温环境下,人们为了更加安全地工作,通常需要穿上高温作业情况下的专用服装也就是热防护服。这种服装主要由三层织物材料构成。第一层与外界环境接触,记为I层,第三层和皮肤之间存在空隙,将空隙层记为Ⅳ层,其余两层为Ⅱ层和Ⅲ层。
1.2 问题的相关信息
(1)题目中给出了专用服装材料的参数值,包括密度、比热、热传导率和厚度。
(2)把假人体内的温度控制在并放在实验室的高温环境中,测量得到了假人的皮肤外侧温度变化情况即附件2。
1.3 需要解决的问题
(1)根据在环境温度为75℃、Ⅱ层厚度为6mm、Ⅳ层厚度为5mm、工作时间为90min情况下得到的假人皮肤外侧的温度(即附件2)以及附件1的相关信息,建立相应的数学模型,计算出其温度分布,并生成假人皮肤外侧温度分布的Excel文件。
(2)在外界环境温度为65℃、Ⅳ层的厚度为5.5 mm时,试确定Ⅱ层的最优厚度,同时满足以下两个条件:在工作时间为60min时,假人皮肤外侧温度不超过47℃;假人皮肤外侧温度超过44℃的总时间不能超过5min。
(3)在外界环境温度为80℃的情况下,确定Ⅱ层的最优厚度和Ⅳ层的最优厚度,同时满足以下两个条件:假人工作30min时,皮肤外侧温度不超过47℃;且皮肤外侧温度超过44℃的时间不超过5min。
2 问题的分析
2.1 问题一的分析
问题一中要求建立假人的皮肤外侧温度的数学模型如图1所示,得出温度分布。
由于温度分布不均匀,因此热量会从温度较高的地方转移到温度较低的地方,也就是各层之间会发生热传导。由于热防护服不能完全阻挡外界的大部分辐射,所以在传热的过程中,热辐射不能被忽略掉。但是空气间隙层的厚度值不是很大,相对来说热对流的影响较小,所以热对流可被忽略掉。另一方面,温度会随时间的变化而发生相应的变化,因此,本题中的热传导属于非稳态导热。因此,在解决问题时要先建立起一个一般情况下的导热微分方程,然后利用热传导定律和能量守恒定律得到热传导微分方程。最后利用热传导微分方程和单值性条件建立起数学模型,得到温度分布情况。
2.2 问题二的分析
对于问题二的分析,问题二要求在满足工作时间为60min时假人皮肤外侧温度小于等于47℃和假人皮肤外侧温度大于44℃的总时间不能超过5min这两个标准的情况下,得出第层的最优厚度。题目中条件改变为外界的环境温度为65℃,Ⅳ层的厚度为5.5mm。因此,由题意知,在确定第Ⅱ层的最优厚度时,要满足两个约束条件,才能合理地求解出第Ⅱ层厚度的最优解。即约束条件1:在工作60min时,假人皮肤的外侧温度不得高于47℃;约束条件2:在确保满足约束条件1的情况下,在开始工作的前5min,假人的皮肤外侧温度不能高于44℃。综上所述,利用模型一中所建立的热传导模型,将环境温度变换为65℃。此问题中我们需要运用模型一中的热传导模型来求得最优解。
2.3 问题三的分析
对于问题三的分析,问题三题目中要求既满足在假人工作30min时,皮肤的外侧温度不大于47℃又满足外侧温度高于44℃的时间不能够超过5min,求解Ⅱ层和Ⅳ层的最优厚度。因此,此题需要在问题二的基础上,考虑环境温度改变为80℃,并且所求的最优厚度变为Ⅱ层和Ⅳ层,此问题中我们运用问题一中的热传导模型。
3 模型的假设
(1)假设题目中所发生的热传递是一维的;
(2)忽略热对流;
(3)假人身体上各处的温度大小相等;
(4)各层之间的温度分布是连续变化的;
(5)热传递是沿垂直于皮肤方向进行的。
4 模型的建立与求解
4.1 问题一的模型建立与求解
4.1.1 问题一的模型建立
在热防护服中的热传递模型:
本题需要建立起高温作业专用服装——热防护服的热传递模型,由题目中已知信息可知:环境温度即为I层左侧开始向热防护服传导温度,Ⅳ层右侧即为假人皮肤的温度。首先对附件2中的90min实验数据进行观察,可以得知初始时刻假人人体初始温度,然后在0s~1745s时间内假人人体温度由逐渐变为并保持不变。最后对0s和5400s这个过程的数据进行整合分析,得到图2假人皮肤外侧温度变化,如图2所示。
由圖2可知,在0s~5400s的时间内,假人皮肤外侧的温度的变化为渐变过程,最终温度保持在了48.08℃,假人皮肤外侧温度随处在环境中的时间的变化而变化,说明了此温度变化的过程为非稳态变化过程。
根据热传递的偏微分方程可得专用服装材料各层的偏微分方程分别为:
式中,CⅠ、CⅡ、CⅢ分别为Ⅰ,Ⅱ,Ⅲ层的比热容;为各层的温度;t为时间;λ1,λ2,λ3分别为Ⅰ,Ⅱ,Ⅲ各层的热传导率;te为在高温中的工作时间;为关于x的取值范围(i=1,2,3,4,5),;r1,r2,r3分别为Ⅰ,Ⅱ,Ⅲ的厚度。
4.1.2 问题一的模型求解
设置热防护服的左右边界条件,右边界温度取自附件2——假人皮肤外侧的测温度表格中的温度,模型的建立中已有边界条件的建立。在附件2中,当温度在0℃~5400℃范围内变化时,选取温度变化点作为温度突变点,构建函数,建立矩阵,再将所构建的函数作为条件,在Matlab软件中进行矩阵的求解与运算。第Ⅳ层的温度可由附件2中所给数据求得。利用有限差分式解得第Ⅳ层与第Ⅲ层之间的函数关系式,再由所确立的热防护服第Ⅲ层的函数关系式,继而推演出热防护服[4]第Ⅱ层的函数关系表达式,同理得出热防护服第Ⅰ层的函数关系表达式。第Ⅰ、Ⅱ、Ⅲ、Ⅳ层所构建的函数表达式分别如下所示:
最后得出温度分布的Excle表格。
4.2 问题二的模型建立与求解
4.2.1 问题二的模型建立
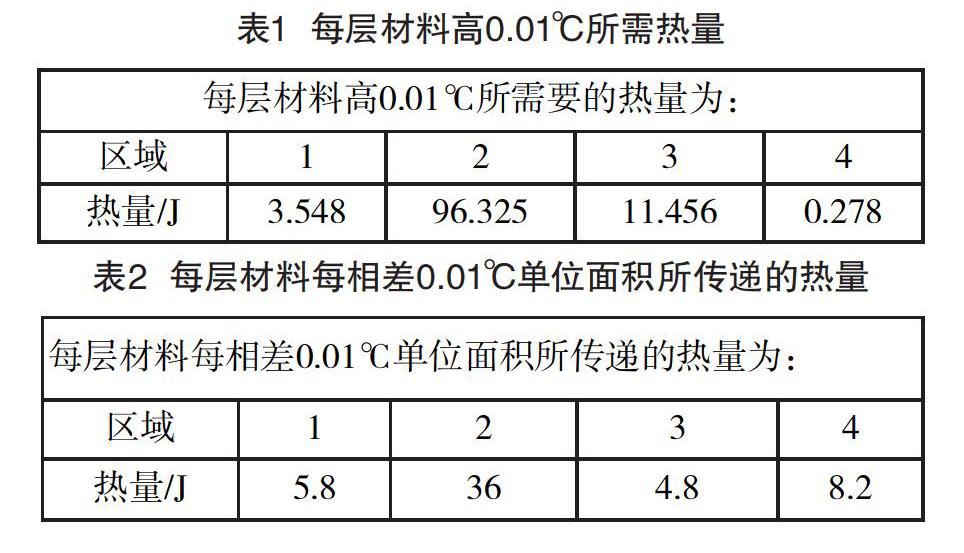
每层材料高0.01℃所需要的热量为:
在附件2中可以得知在工作环境为75℃,工作时间为90min的情形下,假人皮肤外侧温度在578s时,温度超过了47℃,且在274s时,温度超过了44℃,当环境温度改变为65℃时,该模型的最优解为温度在一时间点超过44℃后,在5min之内,假人皮肤外侧温度不得超过44℃。用来表示穿透材料后热辐射减少量的γ消光系数方法,此方法与材料透射率τ和材料厚度ri有关[4-5]。
所以在不同材料的表面的热辐射能量为:
问题二的解决需要利用问题一中所建立的热传导模型。与第一题不同的是,本题中外界环境的温度变为65℃。
4.2.2 问题二的模型求解
4.3 问题三的模型建立与求解
4.3.1 问题三的模型建立
已知问题三中要求在环境温度为80℃,求解Ⅱ层和Ⅳ层的最优厚度,确保工作30min时,假人的皮肤外侧温度不超过47℃,并且超过44℃的时间不得超过5min。因此利用问题二的模型基础,将环境温度改变为80℃,并且把所求的最优厚度改变为第Ⅱ层和第Ⅳ层,外加问题一中的热传导模型进行求解。
4.3.2 问题三的模型求解
利用Lingo软件对以上约束条件进行求解分析,可以得到在环境温度为80℃时,要确保在工作30min时,假人皮肤外侧温度不得高于47℃,且超过44℃的时间不超过5min。则第Ⅱ层和第Ⅳ层的最优厚度分别为:
5 模型的评价与推广
5.1 模型的评价
5.1.1 模型的优点
(1)对于本题所建立的模型与实际相对贴合,从实际出发,在生活中有其实际意义,在日常工作中通用性较强。
(2)利用Matlab软件所绘制的温度分布三维模型,使数据结果更为直观和清晰,操作简洁便利。
(3)所建立的模型数据处理较为精确,利用函数表达式更为准确地表达出各个变量之间的关系。
5.1.2 模型的缺点
由于题中给出的数据较为繁多,处理不易,导致考虑问题以及解决方案不能全面分析,以致会忽略其他影响因素较小的方面。
5.2 模型的推广
通过本题所建立的模型以及利用模型所求的解决结果,我们得到了在一定高温工作环境下,热防护服温度随时间变化而发生的非稳态变化,让人们能够在高温以及其他适当环境中,更好地在生活中得到正确的应用。
参考文献
[1] 卢琳珍,徐定华,徐映红.应用三层热防护服热传递改进模型的皮肤烧伤度预测[J].纺织学报,2018,39(1):25.
[2] 朱方龙,张渭源.新型耐高温服装的热防护性能测试仪[J].产业用纺织品,2006,24(3):36-40,46.
[3] 陶俊,王府梅,刘美娜,等.上装保温性能测试新方法[J].纺织学报,2017,38(6):92-99.
[4] 朱方龙.附加相变材料层的热防护服装传热数值模拟[J].应用基础与工程科学学报,2011,19(4):635-643.
[5] 李东辉,孙创,夏新林.多层隔热材料的热设计方法研究[J].宇航材料工艺,2003.
[6] 四川大学数学学院高等数学、微分方程教研室,高等数学(物理类专业用)[M].北京:高等教育出版社,2015.

