基于因子图的自动驾驶融合定位研究
袁子叶,尹慧琳,伍淑莉
(同济大学 中德学院 电子信息系,上海 201804)
自动驾驶技术在降低交通事故发生率、缓解交通拥堵、实时提供有效最短路径等方面起到了明显的作用[1],其中的关键技术“即时定位与地图构建”(Simultaneous Localization and Mapping,SLAM)也随之备受关注。在SLAM 中,能够根据多个传感器信息,对车辆进行精确定位尤为重要,所以提高即时定位的精确度一直是研究的热点[2]。
对于车辆定位有许多不同的方法,其中利用全球定位系统(Global Positioning System,GPS)与惯性测量元件(Inertial Measurement Unit ,IMU)进行数据融合从而对车辆定位,是最常用的方法之一[3]。GPS 的定位精确度高,且时间以及地域限制对其精度影响较小,但当车辆在有地形遮蔽处驾驶时,GPS信号有可能中断,如隧道、深山等[4]。IMU 能以较高的频率提供多种高精度的导航参数,如速度、加速度、角速度、角加速度等,但由于其数据本身存在噪声干扰,导致位置误差会随时间累计而产生较大偏差,不适合长时间高精度实时定位[5]。然而,由于GPS 数据与IMU 数据具有互补性,所以可通过数据融合实现高精度的实时定位[6]。同GPS 和IMU 数据融合类似的,还有视觉里程计(Visual Odometry,VO)与IMU 的数据融合。VO 主要利用车载相机连续拍摄图片,通过图片中多个明显的特征点与相机的距离对相机进行定位,进而确定车辆位置[7],但在使用VO 定位时,需要提前标定行车地点周围的路标,即照片中的特征点。所以,相对于GPS 定位,VO 需要做大量的前期工作才能确保定位的可靠性[8]。也正是由于VO 需要多个路标点,在对相机定位的同时,可以对陆标点位置进行优化,所以常用于SLAM 中的地图构建。
在处理数据融合问题时,主要使用的方法有加权平均法、卡尔曼滤波法、贝叶斯网络法等[9]。其中,加权平均法模型比较简单,但对于数据类型不同、更新频率不同、噪声模型也不同的多组传感器来说,融合效果并不理想。卡尔曼滤波是最常用的滤波算法,现在许多优化问题都选择采用卡尔曼滤波法解决[10]。卡尔曼滤波是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。卡尔曼滤波非常适合于连续系统,只需要保存当前状态与前一步状态即可。并且,卡尔曼滤波占用内存较小,处理速度快,适合应用于实时系统[11]。但卡尔曼滤波必须已知系统状态方程以及测量方程,并且要求状态方程与测量方程为线性方程,如果方程为非线性,则要先对其进行线性化,才可以使用卡尔曼滤波,但线性化过程本身就导致了误差的产生[12]。贝叶斯网络法是新兴的优化方法,其主要思想是由先验概率以及样本信息得到后验概率,最后由最大后验估计方法对数据进行优化[13]。贝叶斯网络能以有向无环图的形式直观地反映出多组传感器测量值与车辆位置之间的因果关系,在不同的传感器组测量坐标一致时,可以直接对传感器数据进行融合[14],但在计算过程中,发现很多状态之间的关系与所求状态无关,在状态数量过多的情况下采用贝叶斯网络计算将会产生庞大的计算量。同时,当在贝叶斯网络中新增节点时,往往需要对全图进行更新,也增加了优化过程的工作量,不适合用于实时系统。
针对上述问题,考虑到实际应用的准确性和实时性,本文提出采用因子图进行数据融合的方法。因子图同贝叶斯网络一样,也是概率图的一种,它是由KSCHISCHANG 等[15]在2001 年提出的一种二部无向图。因子图可以将一个具有多变量的全局函数分解为几个局部函数的乘积,即在计算过程中可以分离出与当前关系无关的变量[16]。同时,由于因子图与SLAM 底层的优化有更紧密的联系,所以选择用因子图模型进行SLAM 的优化。相比于卡尔曼滤波法和贝叶斯网络法,因子图更直观地表现了不同节点之间的关系。在需要添加状态量时,因子图可以直接在原有图的基础上增添因子,同样,如果测量值可信度较低,或信号丢失,只需要在原图的基础上简单地减少因子即可,不需要特别地编程或者修改模型。因子图的这一特点极大地减少了处理SLAM 问题时的计算量[17]。
1 建立因子图模型
因子图是概率图的一种,其中有两类节点,分别是变量节点与因子节点。本文把车辆位姿、路标位置、传感器测量值等作为变量节点,测量值与位姿之间的概率关系等作为因子节点,建立因子图模型。
1.1 因子图模型介绍
假设在运行的车辆上装备有多种传感器,包括IMU、单目或立体照相机、激光雷达、GPS 等。首先,构建因子图中的变量节点,用xi表示ti时刻的车辆位姿,包括位置、速度、方向,用ci表示ti时刻的标准参数,包括加速度计和陀螺仪的偏差、照相机角度偏差和位置偏差等。此后,可以定义从t1时刻到当前时刻tk所产生的所有状态为:

在有观测地标时,定义第j个观测地标为lj。类似式(1),可以定义从t1时刻到当前时刻tk产生的所有观测地标为lk,则有:

从t1到tk时刻,所有的状态变量可以表示为:

同时,将从t1时刻开始接收到的所有的传感器数据记为Zk,则相应的有:

式中:zi表示在ti时刻接收到的测量值。
构建完所有变量节点之后,开始构建因子节点,因子节点主要描述了变量之间的概率关系。由上述定义得到,当前时刻tk的位姿状态Vk与前一时刻tk-1的状态Vk-1有关,也与tk时刻的标准参数ck有关,同时ck也由前一时刻的ck-1决定,由递推关系以及全概率公式,可以把由观测值Zk得到实际位姿Vk的联合概率函数表示为:

式中:p为联合概率函数。

由式(5)可以看出,联合概率密度函数是非常复杂的,但在实际情况中,当前时刻tk的位姿状态Vk与前一时刻tk-1的状态Vk-1、当前时刻tk的测量值Zk以及标准参数ck有关,即有:

式中:g为由前一时刻tk-1的标准参数ck-1到当前时刻tk的标准参数ck的状态转移方程。
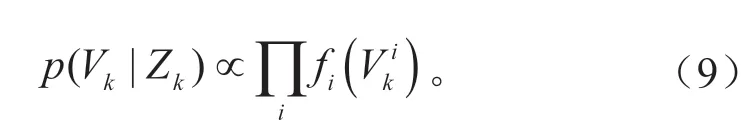
式中:fi为第i组数据的误差方程,在因子图中,fi为变量节点之间的因子节点。
当噪声为高斯白噪声时,有:

式(7)可简单表示为:

在构建完所有的变量节点Vi与因子节点fi之后,建立完整的因子图模型如图1 所示。
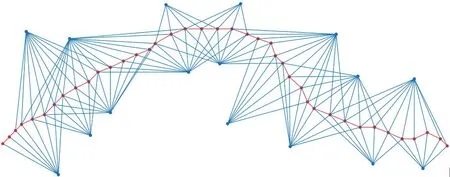
图1 行车路经的因子图模型
在图1 中,红色节点代表由IMU 测量值表示的变量节点,该变量节点构成了链状骨架的主体,两侧的蓝色节点代表由路标位置表示的变量节点,该变量节点是骨架两侧的蓝色线段所代表的二元似然因子,即因子节点,与红色节点相连[18]。
1.2 建立 GPS 及IMU 融合因子图模型
IMU 与GPS 的数据更新频率不同,IMU 相对更新频率较高,具体的数据更新频率由不同的IMU传感器型号所决定。由于IMU 更新较为频繁,考虑以IMU 代表的变量因子作为骨架的主体,构建因子图如图2 所示。

图2 IMU 因子图模型
如图2 所示,xi表示第i时刻车辆的状态,ci表示第i时刻的标准参数。由于IMU 数据会随时间产生误差累积,该误差产生的原因除了测量噪声以外,还有IMU 传感器自身产生的漂移误差,所以需要添加变量节点ci对IMU 传感器的测量值进行矫正。fPrior是一元因子,该因子由式(5)中的p(V0)确定,只和第一步状态x1有关。状态xi+1由xi和ci以及当前时刻测量值zi所确定,因子节点如式(10)所示,其中的为由状态xi和ci到下一状态的状态转移方程[14]。与此类似,因子节点fbias由式(8)确定,为ci到ci+1的转移方程。在实际应用中,可以适当降低标准参数的更新频率,如图3 所示。
骨架构建完成后,为了提高定位的精确度,将GPS 数据与IMU 数据进行融合。在每过一定步长n时,添加因子节点fGPS。其中间隔的步长n由车辆实际装备的IMU 和GPS 的更新频率决定。添加因子节点后的因子图如图4 所示。
如图4 所示,在每个连接了因子节点fGPS的变量节点xi之间,存在多个仅由IMU 数据得到的车辆位姿。考虑将图4 中间隔的步长中的变量节点合并,对因子图化简的结果如图5 所示。

图3 减少参数后的IMU 因子图模型

图4 GPS 及IMU 融合因子图模型

图5 化简后的GPS 及IMU 融合因子图模型
在图5 中,状态xi+1和xi之间实际间隔了nΔt,图中的二元因子节点fEquiv与fIMU类似,但是其中的为第ti时刻到ti+n时刻的状态转移方程。
1.3 建立VO 与IMU 融合因子图模型
随着图像识别技术的发展,利用照片或视频对行车附近的特征点进行标识的技术也日益成熟。反之,如果知道被标识的特征点的具体位置,则可以利用图像得到车辆与特征点间的距离,估计出车辆的具体位置。VO 定位的方式与GPS 不同,GPS 主要通过卫星进行定位,得到的是车辆的全球坐标。利用卫星定位,导致GPS 信号受到空间磁场干扰、建筑物遮蔽等因素的影响,最终导致在某些特定场所或特定时间定位的偏差较大。针对上述问题,不妨考虑用VO 代替GPS。
相比于GPS 信号,利用VO 定位需要有明显的路标作为图像特征,通过对图像与图像或图像与地图之间的特征描述进行匹配,进而确定车辆的确切位置。当然,由于图像特征的局部特性,误匹配的情况还是广泛存在的。根据上文所述,在图2 的基础上,添加路标节点作为变量节点,建立的因子图如图6 所示。
图6 中添加了变量节点li,表示第i个路标。连接路标lj与车辆位姿状态xi之间的因子节点fvision与因子节点fIMU类似,但zk变为车辆位置与特征点距离的测量值。由图6 可知,利用VO 也可以在定位的同时对路标位置进行优化,从而构建车辆驾驶区域的地图。
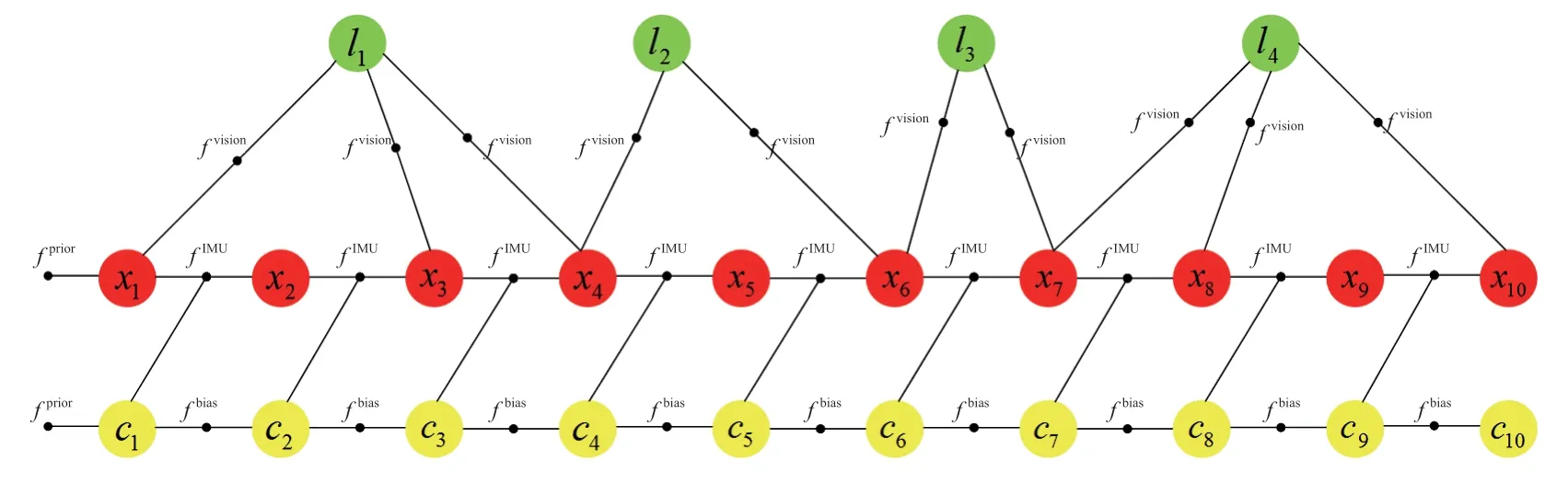
图6 VO 及IMU 融合因子图模型
由于本文主要讨论在SLAM 中的融合定位问题,不考虑构建驾驶区域地图,所以弱化路标在因子图中的作用,仅考虑由路标得到的车辆当前位姿信息,即添加因子节点fVO。又由于VO 与IMU 的数据更新频率也会随具体车载装备而不同,一般情况下,VO 的数据更新频率低于IMU 数据更新频率。根据以上描述,可更新因子图如图7 所示。
与图5 相同,由于因子节点fVO所跨越的所有变量节点均只由IMU 数据优化得到,所以考虑将图7中间的因子节点和变量节点相融合,可得到的因子图如图8 所示。
同样,状态xi+1和xi之间实际间隔了nΔt,图8中的二元因子节点fEquiv中的为第ti时刻到ti+n时刻的状态转移方程。

图7 弱化路标节点后的融合因子图模型

图8 化简后的VO 及IMU 融合因子图模型
2 试验结果及分析
本部分试验测试的硬件环境为内存8 GB,Intel Core i7-8750 处理器,主频2.2 GHz,软件环境为Matlab。试验数据采用KITTI 数据集,KITTI 数据集由德国卡尔斯鲁厄理工学院和丰田美国技术研究院联合创办,是目前国际上最大的自动驾驶场景下的计算机视觉算法测评数据集。试验主要采用右侧的彩色摄像机和GPS 导航系统OXTS 的数据,OXTS 数据同时包括GPS 定位信息和IMU 数据信息。摄像机位置和OXTS 位置如图9 所示。

图9 传感器位置及坐标系
图9 中,红色所标位置为摄像机位置,其中x轴方向为车辆正右方,y轴方向为车辆正下方,z轴方向为车辆正前方。蓝色所标位置为GPS 导航系统OXTS 位置,其中x轴方向为车辆正前方,y轴方向为车辆正左方,z轴方向为车辆正上方。
2.1 GPS 及IMU 定位
由于GPS 数据与IMU 数据均由GPS 导航系统获取,所以本试验的GPS 信号与IMU 信号有相同的时间频率。首先,将GPS 数据与IMU 数据从所获取的OXTS 数据中分离。其次,对GPS 数据进行处理,将GPS 数据由全球经纬坐标,变为地面坐标。最后,将处理后的GPS 数据和IMU 数据带入图5 所示的因子图模型中,得到行车路径的优化结果。流程如图10 所示。

图10 GPS 及IMU 定位
本试验主要根据数据的数量、复杂度等因素,选取了4 组不同的KITTI 数据集进行测试,4 组数据集的数据量分别为76 帧、108 帧、269 帧和313 帧。测试顺序按照数据集中数据信息的数量,由少至多依次排列,测试结果如图11 所示。
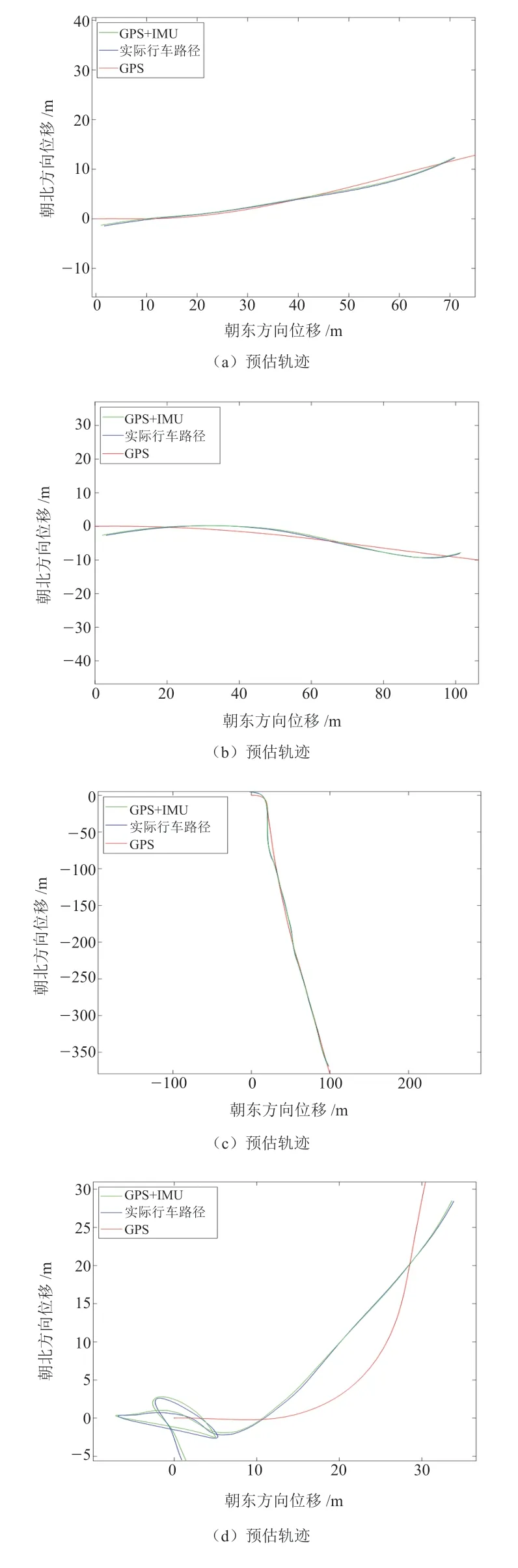
图11 GPS 及IMU 定位后的车辆位姿
图11 分别展示了由4 组数据得到的红色GPS定位路径、绿色的因子图融合后的定位路径以及蓝色的实际行车路经。由图可知,经因子图融合后的定位路径曲线相较于原本的GPS 定位路径曲线,精度更高。在4 组数据中,由图11c 可以观察出第3 组数据相较于其它数据有所不同。在第3 组数据中,车辆在数据采集的初始阶段进行了长时间的转向操作。然而,GPS 并没有明确对当时的车辆位姿进行判断,仅给出了大致定位。但采用因子图对数据融合之后,得到了车辆驾驶过程中明确的车辆位姿。
由第3 组数据中前100 组数据得到的GPS 定位路径与因子图融合后的路径如图12 所示,其中GPS 定位结果在点(0,0)附近 ±0.5 m 的位置 ,并未做明确的移动路径标识。但是由因子图得到的定位结果,明确地表现出车辆经历的位姿。
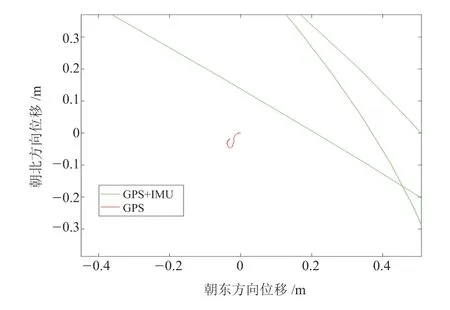
图12 车辆移动幅度较小时的位姿(预估轨迹)
GPS 路径与由因子图融合后的定位路径的具体误差情况如图13 所示。
根据图13 所示的车辆定位误差信息,得到定位误差的均值与均方差值见表1。
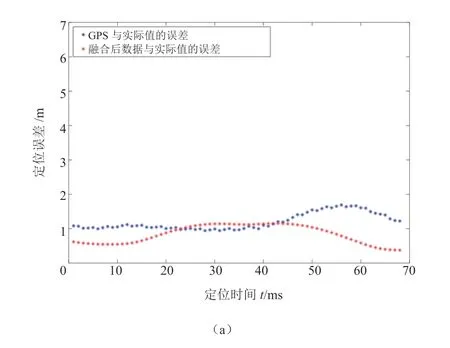
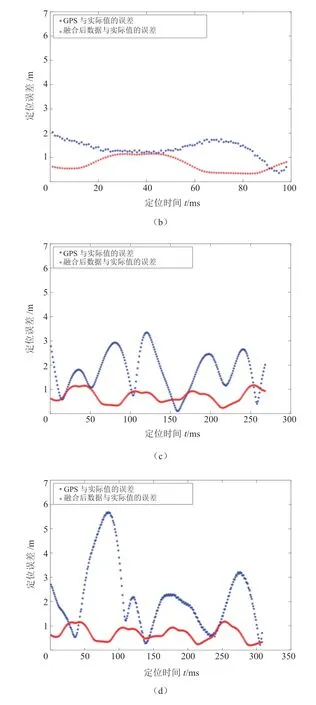
图13 车辆定位误差
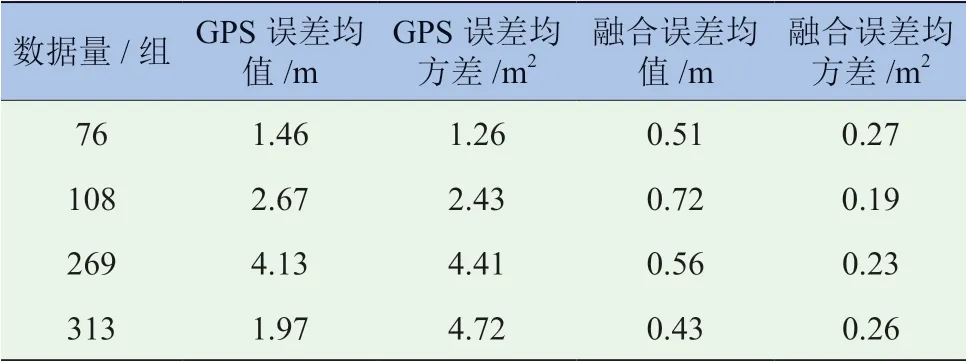
表1 车辆定位误差
由图13 和表1 可知,在第1 组数据中,GPS定位的误差由于数据较少,误差的均值和均方差相对较小。随着数据量的增大,GPS 定位误差均值上升趋势减缓,基本保持在4 m左右,没有明显的上升。经过因子图融合后,定位误差相较于GPS 定位误差有明显减少,误差均值基本可以保持在1 m 左右。综上所述,由因子图对数据进行融合之后得到的车辆位姿更接近真实情况。
2.2 VO 及IMU 定位
VO 及IMU 数据融合的因子图结构与GPS 和IMU 数据融合的因子图结构在骨架部分是相似的,但不同之处在于,VO 数据受到前一时刻和当前时刻车辆位姿的共同影响,GPS 数据仅受到当前时刻测量位姿的影响。
具体流程如图14 所示,首先由彩色摄像机拍摄得到的图像,提取车辆的位姿信息。其次,统一VO 数据和IMU 数据的时间戳。最后,将得到的IMU 数据以及VO 数据带入图8 所示的因子图模型中,得到融合后的车辆位姿。本次试验选取了3组不同的数据进行测试,按照流程图得到的测试结果如图15 所示。
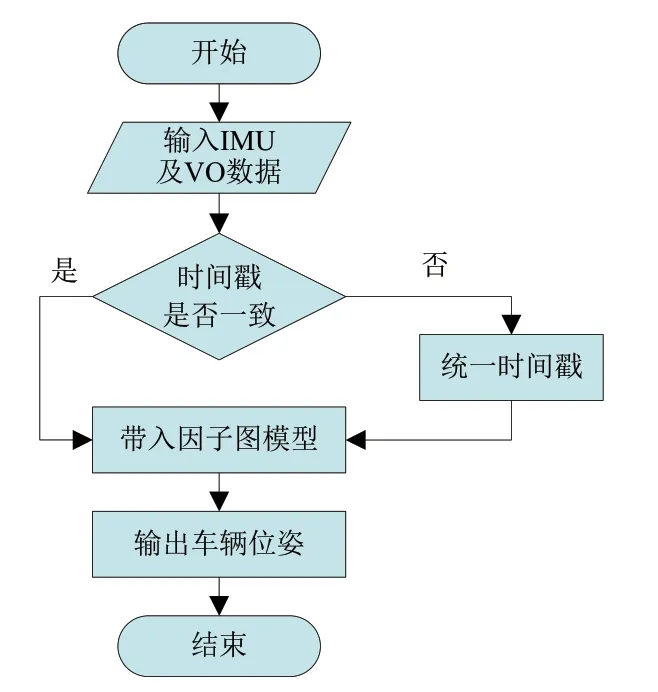
图14 VO 及IMU 定位


图15 VO 及IMU 定位后的车辆位姿
3 结论
为了更精确地实现SLAM 中的定位,本文提出了建立因子图模型的方法,解决了准确判别车辆位姿的问题,包括GPS 与IMU 数据的融合,以及VO 与IMU 数据的融合,这两部分分别利用不同的数据对车辆位姿进行判断。其中,第一部分得到了较为理想的车辆定位结果,第二部分车辆定位结果不太理想,主要原因在于单目VO 对于距离缺乏准确判断,并且随着时间增加漂移误差累积较大。即由于VO 数据的准确度偏低导致定位路径偏差较大,但仍可看出数据融合对车辆定位路径进行了一定的矫正。目前还需要提高VO 数据的准确度,在这方面可以选择双目或多目VO 数据,以期待得到理想的效果。

