基于循环冗余校验的极化码研究

彭文凯 周华

关键词： 极化码; 连续删除译码; 连续删除列表译码; 循环冗余校验码; 译码算法; 译码性能

中图分类号： TN820.1+1?34                    文献标识码： A                       文章编号： 1004?373X（2019）06?0137?05

Abstract： The polar code which has a simple and definite encoding mode and decoding algorithm is proved that it can reach the Shannon limit theoretically， but its successive cancellation decoding （SCD） performs decoding along the single path bit by bit， leading to unsatisfactory practical decoding performance. The successive cancellation list decoding （SCLD） is a modified algorithm of the SCD， which improves the decoding performance of the polar code at the cost of increasing the decoding complexity. The combination of SCLD and the cyclic redundancy check （CRC） can further reduce the probability of decoding errors in the multiple paths of the SCLD without increase of the decoding complexity. Based on this， the performance difference generated by different combinations of CRC codes with polar codes is analyzed in this paper， so as to obtain appropriate combinations of CRC codes with polar codes.

Keywords： polar code; successive cancellation decoding; successive cancellation list decoding; cyclic redundancy check code; decoding algorithm; decoding performance

极化码（Polar codes）是Erikan在2009年提出的基于信道极化理论的一种编译码方式，该编译码具有明确的编码和译码算法数学公式[1]，Erikan在理论上证明了该编译码方式能够达到香农极限。由于极化码在理论上的优异性能，该编译码一经提出便成为众多领域的研究热点。美国当地时间2016年11月17日凌晨0点45分，在美国内华达州里诺召开的3GPP RAN1 87次会议的5G短码方案讨论中，以中国华为公司主推的极化码方案成为5G控制信道eMBB场景（上行/下行）编码方案。

作为极化码的原始算法，SC译码（Successive Cancellation Decoding）[2]在实际仿真实验中的译码性能并不如传统的LDPC码和Turbo码。SCL译码（Successive Cancellation List Decoding）[3]作为SC译码的改进算法，以付出一定的译码复杂度为代价，通过保留尽可能多的路径来获得正确的译码序列，从而提高译码性能。但是随着保留路径的增加，一方面译码复杂度呈倍数增长，另一方面错过正确译码序列的概率也随之增加。CRC?SCL译码[4]是在SCL译码基础上改进的译码算法，该算法在不增加译码复杂度的情况下，能一定程度上提高SCL译码算法的性能。仿真结果表明并不是所有的CRC（Cyclic Redundancy Check）都可以对极化码产生积极的影响，不同的CRC对不同码长的极化码产生的译码性能也不尽相同。

本文以SCL译码算法为基础，在译码复杂度不增加的基础上结合不同的CRC码进行仿真，以找出不同码长下尽可能提高SCL译码性能的CRC，并分析CRC对SCL译码的性能影响。

1  极化码的编码和译码算法

譯码树为SCL译码的另一个概念[7]，每个码长为N的极化码均可以对应一个N层的译码树，译码树中任意上下两个节点之间的边对应一个译码码元，用0或1表示，从根节点到任意叶节点形成的路径对应一段完整的译码序列。每个节点均对应一个路径度量值，根节点为路径度量值的初始值，即[PM?=0]，叶节点为整个译码序列最终的路径度量值。图1为码长为4的译码树。

译码时，从根节点出发按广度优先的方法向下层扩展，每一层向下一层扩展时，当前层每一个节点均有0和1两种选择，每种选择结合前面已经译码出来的码元使用式（4）或式（5）可以计算出当前码元的对数似然比，结合式（3）求出该路径的度量值;然后保留路径度量值较大的L条路径继续向下层扩展直到叶节点;最后从保留的L条路径中选择最大路径度量值对应的路径作为最后的译码序列。

SCL译码算法[8]的详细过程如下：

1） 初始化：初始化路径度量值，即[PM?=0]。

2） 路径扩展：将之前i-1层保留的路径向第i层扩展，计算第i层所有节点选择0或1的路径度量值，并保留所有扩展后的路径。

3） 路径选择：将步骤2）中保留的路径按路径度量值从大到小进行排序，如果此时的路径数量小于L，则保留所有路径，否则保留路径度量值较大的L条，其余的路径不再向下层扩展。

4） 扩展结束：如果译码进行到第i层且i

SCL译码作为SC译码的改进算法，从理论上可以解决SC译码由于单路径的局限性，从而提高译码性能，然而随着保留路径的增加，译码复杂度也随之提高。同时会出现正确的译码序列存在于保留路径中，但其路径度量值并不是最大值，而最大路径度量值对应的序列不是正确的译码序列，保留路径越多，出现这种译码错误的概率也越高。

2  CRC?SCL译码

CRC是一种利用除法和余数原理来进行检查译码错误的校验码[9?10]。实际应用时，发送端计算CRC值并随数据一同发送给接收端，接收端对接收到的软信息进行译码，并检查得到的译码序列能否通过CRC校验。对于一个给定的（N，K）码，可以证明存在一个最高幂次为N-K=R的多项式G（x）。根据G（x）可以生成K位信息的校验码，G（x）为这个校验码的生成多项式。若发送信息用信息多项式C（x）表示，将其整体左移R位，则可表示成C（x）*2R，左移R位后C（x）的右边会空出R位，即校验码的位置，通过C（x）*2R除以生成多项式G（x）得到的余数就是校验码。

SCL译码的信息位为K，码率为[KN]，该算法在译码时会保留L条路径，若编码时在M位信息比特后添加K-M位的检验码可以得到K位含有检验码的信息比特序列，此时码率为[MN]。将含有检验码的序列作为信息比特序列与固定比特序列混合后进行编码，经过信道传输后译码器对接收到的软信息进行译码可以得到L条译码序列，提取信息位上的码元可以得到L条含有K-M位校验码的信息比特序列，如图2所示。将这L条信息比特序列进行CRC校验，将能通过CRC校验的序列除去检验码作为最后的译码序列，若保留的L条信息比特序列都不能通过CRC校验，则将路径度量值最大的序列作为最后的译码序列。CRC?SCL译码系统结构[11]如图3所示。

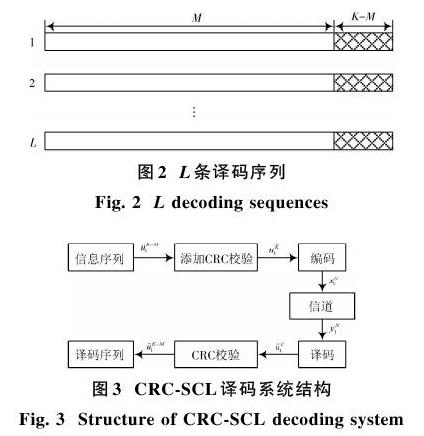
CRC?SCL译码算法[12]的前3个步骤与SCL译码算法相同，只需将最后一步更改如下：

4） 扩展结束：如果译码进行到第i层且i

5） CRC校验：若L=1，则该路径就是最后的译码序列，若L>1，对保留的L条路径进行校验，通过CRC校验的序列作为最后的译码序列，若保留的L条路径都不能通过CRC校验，则将最大路径度量值对应的路径作为最后的译码序列。

3  仿真结果分析

该仿真实验主要以SCL译码为基础，以Matlab软件为平台，所有仿真实验都在AWGN信道下完成，调制方式为BPSK调制。

图4显示了SCL译码在不同的保留路径数下所产生的性能差异，该仿真实验的码长为256，信息比特长度为128，码率为0.5，路径分别为L=1，4，8。从该仿真结果可以看出路径为4和路径为8时的译码性能明显优于路径为1时的译码性能。然而路径为8时的译码复杂度是路径为4时的译码复杂度的2倍，但是两者的譯码性能却相差不大。

图5显示了不同码长对SCL译码性能的影响，该仿真实验的码率为0.5，保留路径数均为4。信噪比小于1.1 dB时，码长为256时的译码性能略优于码长为1 024时的译码性能，当信噪比大于1.1 dB时，码长为1 024时的译码性能优于码长为256时的译码性能，且随着信噪比的增加，码长为1 024时的误码率和码长为256时的误码率差异也随之增大。

图6显示了SCL译码和CRC?SCL译码在保留路径分别为4，8和16时的性能差异。路径L=4时，在信噪比大于3.4 dB的部分，CRC?SCL译码的译码性能优于SCL译码的译码性能;路径L=8时，在信噪比大于2.7 dB的部分，CRC?SCL译码的译码性能优于SCL译码的译码性能;路径为16时，在信噪比大于2.4 dB的部分，CRC?SCL译码的译码性能优于SCL译码的译码性能。造成这种结果的原因是CRC?SCL译码在编码过程中增加CRC冗余导致码率降低，此时码元的能量不能使CRC?SCL译码降低极化码的误码率;当信噪比足够大时，码元的能量也随之增大并且能够满足CRC?SCL译码对极化码产生有利影响，所以在高信噪比区域，CRC?SCL译码的译码性能优于SCL译码的译码性能。

图7显示了在码长为256，保留路径为4时，CRC?SCL译码方式在不同CRC校验码下所产生的性能差异，在信噪比小于2.6 dB的部分，8位CRC校验码的CRC?SCL译码的误码率比其他CRC?SCL译码的误码率更低;而在信噪比大于2.6 dB的部分，12位CRC校验码的CRC?SCL译码的误码率最低。

4  结  论

本文研究了极化码的编码和译码原理，对不同码长的极化码在SCL译码下进行仿真，分析了码长和路径数L对极化码性能的影响。在此基础之上对CRC?SCL译码和SCL译码的仿真结果进行对比分析，分析了CRC?SCL译码在低信噪比部分和高信噪比部分对极化码的性能产生不同影响的原因。同时在码长N=256时，将不同长度的CRC校验码对极化码的性能影响进行仿真，通过大量的仿真数据证明，在码长N=256时，12位CRC校验码的CRC?SCL译码的译码性能较好。

参考文献

[1] ARIKAN E. Channel polarization： a method for constructing capacity?achieving codes for symmetric binary?input memoryless channels [J]. IEEE transactions on information theory， 2009， 55（7）： 3051?3073.

[2] XING C， WANG B， ZHAO S M. A reduced?complexity successive?cancellation decoding algorithm for polar codes [C]// Proceedings of 6th International Congress on Image and Signal Processing. Hangzhou： IEEE， 2013： 5?10.

[3] Tal I， VARDY A. List decoding of polar codes [C]// Proceedings of IEEE International Symposium on Information Theory， St. Petersburg： IEEE， 2011： 1?11.

[4] CAO M， ZHAO S， ZHAO S M. Multiple CRC?aided variable successive cancellation list decoder of polar codes [J]. The journal of China Universities of Posts and Telecommunications， 2017， 24（2）： 83?88.

[5] HASHEMI S A， BALATSOUKAS?STIMMING A， GIARD P， et al. Partitioned successive?cancellation list decoding of polar codes [C]// Proceedings of IEEE International Conference on Acoustics， Speech and Signal Processing. Shanghai： IEEE， 2015： 1?4.

[6] BALATSOUKAS?STIMMING A， PARIZI M B， BURG A. LLR?based successive cancellation list decoding of polar codes [J]. IEEE transactions on signal processing， 2015， 63（19）： 5165?5179.

[7] CHEN K， NIU K， LIN J R. A reduced?complexity successive cancellation list decoding of polar codes [C]// Proceedings of 77th Vehicular Technology Conference （VTC Spring）. Dresden： IEEE， 2013： 1?5.

[8] FAN Y Z， XIA C Y， CHEN J， et al. A low?latency list successive?cancellation decoding implementation for polar codes [J]. IEEE journal on selected areas in communications， 2016， 34（2）： 303?317.

[9] ZHANG Q S， LIU A J， PAN X F， et al. CRC code design for list decoding of polar codes [J]. IEEE communications letters， 2017， 21（6）： 1229?1232.

[10] LI S B， LU L J， DENG Y Q， et al. A reused?public?path successive cancellation list decoding for polar codes with CRC [J]. IEEE communications letters， 2017， 21（12）： 2566?2569.

[11] MURATA T， OCHIAI H. On design of CRC codes for polar codes with successive cancellation list decoding [C]// Proceedings of IEEE International Symposium on Information Theory. Aachen： IEEE， 2017： 1?6.

[12] YU Q P， SHI Z P， YAN Q H， et al. Hybrid parity?check and CRC aided SCL decoding for polar codes [C]// Proceedings of IEEE International Conference on Internet of Things （iThings） and IEEE Green Computing and Communications （GreenCom） and IEEE Cyber， Physical and Social Computing （CPSCom） and IEEE Smart Data （SmartData）. Chengdu： IEEE， 2016： 11?15.