湖北省自然灾害社会脆弱性综合测度及时空演变特征

阮鑫鑫，付小林，侯俊东，董雅深，吕 军

(1.中国地质大学(武汉)经济管理学院，湖北 武汉 430074；2.中国地质调查局武汉地质调查中心，湖北 武汉 430205)

湖北位居华中腹地，地处长江中上游，省内自然灾害种类多、频率高、分布广，局部地区灾情严重[1],各类自然灾害的发生给社会带来了重大的人员伤亡和经济损失，严重威胁了区域经济的可持续发展。因此，如何减灾抗灾、降低灾害损失，成为科研工作者积极探索的重要课题之一。在传统的自然灾害风险管理研究领域，学术界主要研究气象气候特征、生态环境、地质地貌等不同灾害类型，而缺少对承灾体自身脆弱性的研究。随着人类社会活动的日益活跃，自然灾害研究开始从致灾因子的自然脆弱性过渡到对承灾体的社会脆弱性，由此，自然灾害社会脆弱性术语得到广泛应用。自然灾害社会脆弱性作为灾害研究的新视角，引起了当今国际社会和学术界的广泛关注[2-5]。

脆弱性概念起源于自然灾害的研究[6],20世纪80年代，Timmerman首次提出了脆弱性的概念，并被广泛应用于各个研究领域。学术界较为普遍的观点认为，脆弱性是系统受到外界冲击的敏感性以及因应对能力不足导致系统机制变化的一种属性，这一属性既可以表现在自然环境中，又可以表现在社会情景中。因此，Blaikie根据不同学科领域视角，将脆弱性进一步划分为自然脆弱性和社会脆弱性。受资料限制，早期国内学者注重自然灾害的自然脆弱性研究，而忽视了自然灾害可能带来的社会影响[7-9]。在城市可持续发展战略的引导下，学者们对自然灾害的研究焦点已向人类社会系统转移，以社会维度分析脆弱性的本源。由于不同学科领域的研究对象和研究视角存在差异，各研究领域学者对社会脆弱性的概念认定、形成机制、表现特征、评估方法等存在不同的认知和理解。目前，针对社会脆弱性主要有“冲击论”、“风险论”、“社会关系呈现论”和“暴露论”等几种典型定义[10-11]。如George等[12]、Cutter等[13]认为，社会脆弱性是人类社会系统在面对现存或预期将要发生的灾害事件时所遭受的潜在损失；Waley[14]、Turner等[15]认为，社会脆弱性是人类社会系统在面对灾害事件时遭受损失的可能性；Cutter等[16]、周利敏[17]认为，社会脆弱性是人类社会系统在灾害事件发生前的一种既存状态，是社会系统内在特征的固有属性；林涓涓等[18]、李文彬等[19]认为，社会脆弱性是社会系统暴露于灾害事件的潜在因素和损伤程度。

综合国内外学者的社会脆弱性研究成果，本文认为社会脆弱性是系统面对已经发生或预期未来将要发生的灾害事件的扰动所体现出来的容易遭受损失的程度，以及抵御不利影响的应对能力的大小[20]。可以细化为以下两个方面来理解：①人类社会系统遭遇灾害事件时的敏感性，体现在系统受到灾害事件冲击时，其内部要素暴露于灾害事件不利影响下的受灾程度，最终以灾害损失的形式表现出来；②人类社会系统遭遇灾害事件时的应对能力，体现在人类完善和优化系统内部要素，对系统中现存或预期的灾害事件的扰动作出响应的能力。

社会脆弱性评价是对人类社会系统自身结构和功能进行探讨，评价人类社会系统受到灾害事件的不利影响以及抵抗不利影响的能力，可以推动人类社会的可持续发展。随着相关研究的深入，不同领域的学者对社会脆弱性定量评价的角度不同，评价模型呈现出多元化、复杂化的发展趋势[21]。目前，社会脆弱性量化评价方法主要有基于历史灾情评价方法、基于指标体系评价方法和基于灾害损失曲线评价方法等[22-23]。其中，基于指标体系评价方法主要从自然灾害社会脆弱性的内在成因、外在特征等方面选取评价指标，然后利用数理统计方法对各项指标进行量化和赋权，最后利用数学模型估算评价单元的社会脆弱性指数。该评价方法计算过程简便、可操作性强，适用于探究不同空间尺度和时间跨度的社会脆弱性，能够展现社会脆弱性的时空演变特征[28]。但是，该评价方法在指标的选取、指标数据的处理、指标的赋权以及评价结果的计算等方面尚未形成统一标准，由于存在人为的主观性判断，使评价指标体系等出现信息不完备和信息交叉重叠的情况[29]。为此，本文首先基于社会脆弱性的理论内涵，结合自然灾害的社会属性，以湖北省12个地级市为研究对象，在参考国内外研究成果的同时，综合考虑研究单元的有限性、评价指标的模糊性以及相关指标数据的可靠性和可获得性，基于文献归纳法总结出31个使用频率较高的评价指标，并利用相关分析和主成分分析对原始指标进行筛选[30-31]，得到13个具有代表性的相互独立的重要指标;然后采用熵权法对各项指标赋权，利用二级模糊综合评价方法计算湖北省各地级市自然灾害社会脆弱性指数，进而对湖北省自然灾害社会脆弱性进行合理评估；最后运用数理分析工具和ArcGIS空间分析技术，研究了湖北省各地级市自然灾害社会脆弱性的时空演变特征，以提高城市韧性，积极开展减灾抗灾的常态管理，为实现城市可持续发展提供有价值的参考信息。

1 自然灾害社会脆弱性评价方法

1.1 研究单元的选取

鉴于指标数据的可获得性，本文选取湖北省12个地级市作为基本研究单元，按行政区划，将12个地级市划归鄂东、鄂中、鄂西三大区域。其中，鄂东地区包括武汉、黄石、鄂州、黄冈和咸宁；鄂中地区包括荆门、荆州、孝感和随州；鄂西地区包括十堰、宜昌和襄樊。考虑到行政区划的变更(2010年“襄樊”更名为“襄阳”)，本文将襄樊2010年以前年份的数据作为襄阳同期数据。

1.2 数据来源

为了能够客观地反映湖北省自然灾害社会脆弱性特征，本文采取统计指标收集法，根据现有文献中相关指标出现的频率和数据的可获得性，结合湖北省各地级市的实际情况，以中国统计局所编制的2001—2016年中国城市统计年鉴和湖北省各地级市统计年鉴为基础，从人口状况、生活水平、产业结构、基础设施、教育资源、医疗条件等13个方面着手，初步归纳并总结出使用频率较高的31个评价指标用来测度自然灾害的社会脆弱性，详见表1。

表1 自然灾害的社会脆弱性评价指标

1.3 评价指标的筛选及权重的确定

1.3.1 评价指标的筛选

由于自然灾害社会脆弱性评价指标主要依托于中国统计局所编制的城市统计年鉴资料，大量的评价因子存在信息交叉重叠，并且评价因子个数大于样本个数，故不适合将自然灾害社会脆弱性评价指标直接作为评价因子。为了遵循评价指标设计SMART准则(即满足特定性、可测性、可得性、相关性、可跟踪性)，有必要对自然灾害社会脆弱性评价指标进行相关分析，并在此基础上利用主成分分析的降维思想筛选出具有代表性的关键评价指标，从而构建一套科学、合理、能反映湖北省自然灾害社会脆弱性的评价指标体系[32]。

首先，对2001—2016年湖北省12个地级市自然灾害社会脆弱性标准化后的评价指标进行秩次相关分析，排除两个指标之间相关系数大于0.8的情况；然后，在此基础上利用主成分分析法对剩余的18个评价指标进行第二次筛选，由于指标载荷值的大小反映指标对评价结果的影响程度，其绝对值越大，表明指标对主成分的解释越明确，指标越应保留；最后，筛选出13个具有代表性的相互独立的重要评价指标,构建自然灾害的社会脆弱性综合评价指标体系，见表2。

表2 自然灾害的社会脆弱性综合评价指标体系

考虑到人类社会系统在面对自然灾害时，自然灾害的社会脆弱性必然受到特定的经济状况、社会地位、教育程度、人口结构等多种复杂因素的影响，也就是说，在同一致灾强度下，不同地区自然灾害社会脆弱性程度不同，灾害事件造成的直接经济损失也不相同，通常情况下敏感性越强，自然灾害社会脆弱性越高，应对能力越强，自然灾害社会脆弱性越低。因此，敏感性相关指标与自然灾害的社会脆弱性呈正相关，敏感性越强，自然灾害社会脆弱性越高，故属于正向指标；应对能力相关指标与自然灾害的社会脆弱性呈负相关，应对能力越强，自然灾害社会脆弱性越低，故属于负向指标[33]。

1.3.2 数据的标准化处理

由于自然灾害社会脆弱性评价指标体系中各项指标的类型、量纲、数量级以及指标的正负取向均有所差异，为了保证评价指标具有可比性和可度量性，本文选用极差标准化法按正向指标和负向指标将原始数据进行无量纲化处理。

对于正向指标，有：

对于负向指标，有：

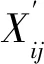
1.3.3 评价指标权重的确定

在对上述自然灾害社会脆弱性综合评价指标体系的测度中，可以利用主观赋权法和客观赋权法确定各评价指标的权重，前者依据评价者对各评价指标的主观认知进行赋权，如德尔菲法、层次分析法等；后者则是根据各评价指标数据信息来决定其权重，如熵值法、主成分分析法等[34]。在客观赋权法中，由于定量与定性相结合的熵值法可消除人为主观臆断的影响，能够充分反映指标信息的效用价值，因此本文选用熵值法来确定各评价指标的权重，其主要步骤如下：

(1) 计算第i个地级市第j项指标的比重：

(2) 计算第i个地级市第j项指标的熵值：

(3) 计算第j项指标的差异系数：

bj=1-aj

(4) 计算第j项指标的熵权：

上式中:i表示湖北省地级市的个数，0≤i≤m;j表示评价指标的个数，0≤j≤n。

本文借助MATLAB 2014a软件，计算得到2016年湖北省自然灾害社会脆弱性各项指标的权重值(以2016年湖北省数据为例计算得到的各项指标权重值)。

表3 2016年湖北省自然灾害社会脆弱性各项指标的权重值

1.4 自然灾害的社会脆弱性指数计算

考虑到评价自然灾害社会脆弱性所涉及的评价指标较为复杂和模糊，且各项评价指标所占的权重较小，本文选用二级模糊综合评价模型对评价指标进行梳理和分类，在敏感性和应对能力的基础上逐步划分层次，并在小范围内精确定位各评价指标的主次程度，进而明确权向量和隶属度矩阵，最终计算得到自然灾害的社会脆弱性指数[35-38]。二级模糊综合评价方法的具体步骤如下：

(1) 构建因素集U并对其进行分类:根据自然灾害社会脆弱性评价指标体系的准则层，确定因素集为U={U1,U2}={敏感性，应对能力},将因素集U1、U2按照其相关属性进一步划分，得到U1={u11,u12,…,u14}={人口密度，第一产业GDP的比重，…，城乡居民收入差距指数}，U2={u21,u22,…,u29}={人均地区生产总值，人均铺装道路面积，…，国际互联网用户普及率}。

(2) 构建因素评判集:根据自然灾害社会脆弱性的评价结果，参考其他文献的相关方法，采用中位数法和平均值法确定评判集的分级标准[39],将自然灾害社会脆弱性的每个具体评价指标分为5个等级，表示为V={v1,v2,v3,v4,v5}，其中v1,v2,…,v5为连续的等级标准，下标的大小直接反映了等级的高低。

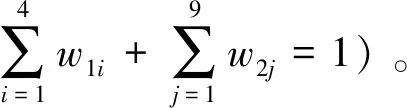
(4) 确定隶属函数:隶属度矩阵R代表了每个评价指标对每个评判等级的隶属度，可以反映因素集U和因素评判集V之间的模糊关系，故隶属度是社会脆弱性指标值和评判等级的函数。通过查阅参考文献，结合自然灾害社会脆弱性综合评估的特点，本文选用偏小型降半梯形分布和偏大型升半梯形分布构建如下隶属函数：

式中：xi(1≤i≤13)表示湖北省某个地级市的第i项社会脆弱性评价指标；λj(1≤j≤5)为各项指标5个评价等级标准的代表值。

(5) 构建隶属度矩阵，逐一评价因素集：首先，进行一级模糊综合评价，根据以上公式可以得到每项指标对各个因素评判集的隶属度，以因素集U1为例，设一级模糊综合评价的隶属度矩阵为

式中：rkj表示第k项指标对第j个评价等级的隶属度；隶属度矩阵R1表示因素集U1中各项指标对每个评判集的隶属性集合。

根据因素集U1各项指标的权重集和隶属度矩阵R1，可以得到因素集U1的模糊综合评价向量B1为

B1=W1·R1

=(b11,b12,…,b15)

以此类推，再评价指标数量较多的因素集U2，得到因素集U2的隶属度矩阵R2和模糊综合评价向量B2,由此形成综合评价隶属度矩阵R：

结合因素集的权重w={w1,w2}，进行二级模糊综合评价，得到综合评价向量，具体表示为B=w·R。

为了更加精确地分析评价结果，本文采用加权平均值法计算自然灾害的敏感性指数、应对能力指数和社会脆弱性指数。加权平均值法的计算公式如下：

式中:N表示加权平均值;k表示因素评判等级;bk表示相应的隶属度。

本文以2016年武汉市的相关指标为例，构造因素集U1和U2的隶属度矩阵R1和R2如下：

因素集U1、U2相对于目标层U的权重集为

w={0.447,0.553}

u11,u12,…,u14各项指标相对于因素集U1的权重集为

w1={0.158,0.122,0.263,0.458}

u21,u22,…,u29各项指标相对于因素集U2的权重集为

w2={0.108,0.182,0.096,0.068,0.078,0.085,0.205,0.106,0.072}

依据隶属函数公式，可以求出因素集U1、U2的模糊综合评价向量B1和B2，从而得到综合评价隶属度矩阵R和综合评价向量B：

B1=w1·R1=(0.000,0.047 9,0.555 2,0.261 5,0.136 4)

B2=w2·R2=(0.722,0.069 3,0.137 0,0.072 0,0.000)

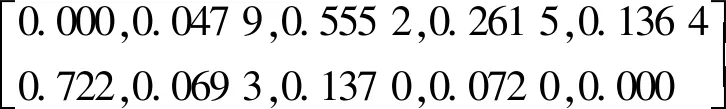
B=w·R=[0.399,0.060,0.324,0.157,0.061]

最后，采用加权平均值法计算得到湖北省武汉市自然灾害的敏感性指数为3.486、应对能力指数为1.559、社会脆弱性指数为2.294。

同理，可以计算得到2016年湖北省其他各地级市自然灾害的敏感性指数、应对能力指数和社会脆弱性指数，详见表4。

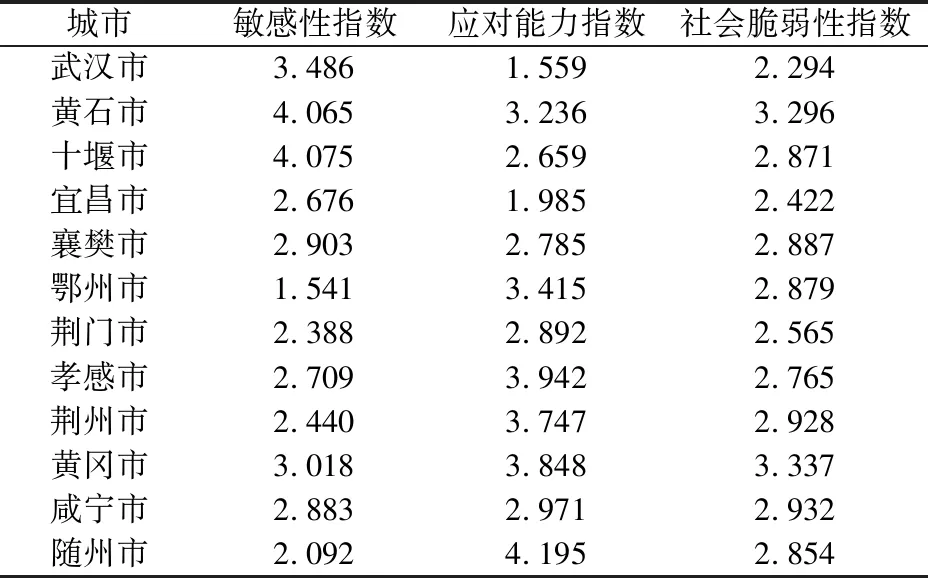
表4 2016年湖北省各地级市自然灾害的敏感性指数、应对能力指数和社会脆弱性指数

2 湖北省自然灾害社会脆弱性的时空演变特征分析

2.1 湖北省自然灾害社会脆弱性的时序变化分析

本文将湖北省12个地级市的自然灾害社会脆弱性指数进行算术平均，计算得到湖北省自然灾害的社会脆弱性指数，并绘制2001—2016年湖北省自然灾害社会脆弱性的变化趋势图，见图1。

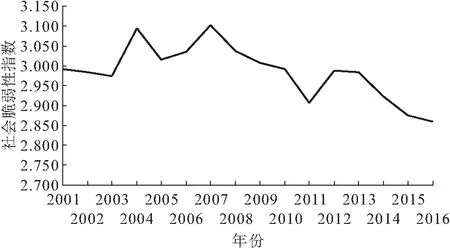
图1 2001—2016年湖北省自然灾害社会脆弱性的变化 趋势图Fig.1 Trends of social vulnerability to natural disasters in Hubei Province during 2001—2016

由图1可见，从整体上看，湖北省自然灾害社会脆弱性指数以波动递减为主，呈现出“由大差距高社会脆弱性向小差距低社会脆弱性演变”的趋势；2001—2016年湖北省自然灾害社会脆弱性指数可以分为两个阶段：第一阶段(2001—2008年)，自然灾害社会脆弱性指数呈波动缓慢上升的趋势，个别年份下降，从2001年的2.992上升到2008年的3.307，平均每年上升0.039，这是因为这一阶段湖北省人口处于较快增长阶段，社会人口基数的压力大，且伴随着城镇化的快速推进，大量人口涌向城市，使得自然灾害社会脆弱性指数较高且变化缓慢；第二阶段(2009—2016年)，湖北省城市的经济规模不断扩大、产业结构逐步优化、城市化效率逐渐提高，使得自然灾害社会脆弱性指数明显下降，从2009年的3.008减小到2016年的2.836，较2009年下降了5.72%。

本文基于数理分析的视角，利用极差、标准差、变异系数、泰尔系数等指标对湖北省自然灾害社会脆弱性的区域差异性进行分析[40-41]，其具体计算公式如下：

极差R=xmax-xmin

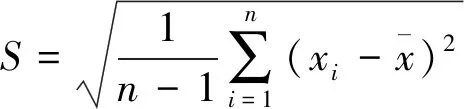
湖北省各地级市间的泰尔系数

T=∑(gi/G)·log[(gi/G)/(pi/P)]

本文结合2001—2016年湖北省各地级市自然灾害社会脆弱性指数，并利用上述相关公式计算得到湖北省自然灾害社会脆弱性的极差、标准差、变异系数和泰尔系数，其计算结果见表5。

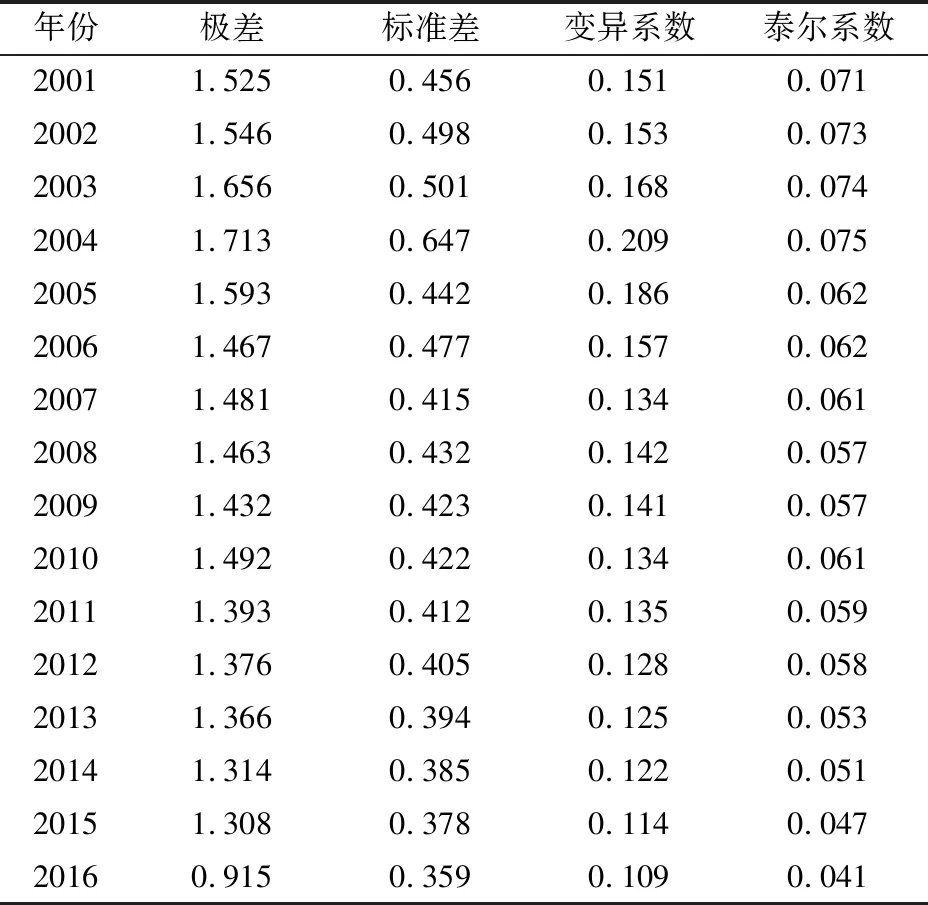
表5 2001—2016年湖北省自然灾害社会脆弱性的极差、标准差、变异系数和泰尔系数

由表5可知，湖北省自然灾害社会脆弱性的极差呈现先增大再减小的特点；自然灾害社会脆弱性的标准差从2001年的0.456上升到2004年的0.647，而后又下降到2016年的0.359，说明湖北省自然灾害社会脆弱性的绝对差异呈现出先增大后缩小的变化趋势，意味着湖北省各地级市间自然灾害社会脆弱性的差距不断缩小，呈现出均衡发展的态势；自然灾害社会脆弱性的变异系数呈现先增大、再减小、再增大、再减小的“M型”的变化趋势，意味着湖北省自然灾害社会脆弱性的相对差异呈现波动下降的特点；自然灾害社会脆弱性的泰尔系数呈现先增后减、再增再减的变化趋势，进一步验证了2001—2016年间湖北省自然灾害社会脆弱性呈现相对差异变化的特点，综合绝对差异和相对差异，表明湖北省自然灾害社会脆弱性经过16年的螺旋式发展，由区域差距大的高社会脆弱性向区域日趋均衡的中低社会脆弱性格局演变。

2.2 湖北省自然灾害社会脆弱性的空间变化分析

湖北省自然灾害社会脆弱性存在明显的“极差化”，武汉市的自然灾害社会脆弱性最低，而黄冈市的自然灾害社会脆弱性最高，但整体处于中度社会脆弱性状态。例如以2016年为例，湖北省自然灾害社会脆弱性指数的平均值为2.836，其中：武汉市的自然灾害社会脆弱性指数最低，为2.294；其次为宜昌市，自然灾害社会脆弱性指数为2.422；随州市、鄂州市、十堰市、襄樊市处于中等社会脆弱性级别；荆州市、咸宁市则由于城镇登记失业率较高、城乡居民收入差距指数较大，承灾体暴露的数量多、价值大、范围广，而抗灾救灾所需的经济资源和人力资源不足，在自身敏感性较强、应对能力欠缺的情况下，综合来看其自然灾害社会脆弱性较高；黄冈市的自然灾害社会脆弱性最高，可能的原因是一方面该市的经济基础薄弱、教育资源匮乏、医疗条件落后、城镇化进程缓慢，极大地削弱了其社会系统的应对能力，另一方面黄冈市产业结构落后、第一产业占比偏大、经济发展动力不足，且在人口增长和老龄化加速的压力下，其城乡居民收入失衡，城镇登记失业率居高不下，大大增加了其敏感性，使得该市极易受到自然灾害的影响和冲击。

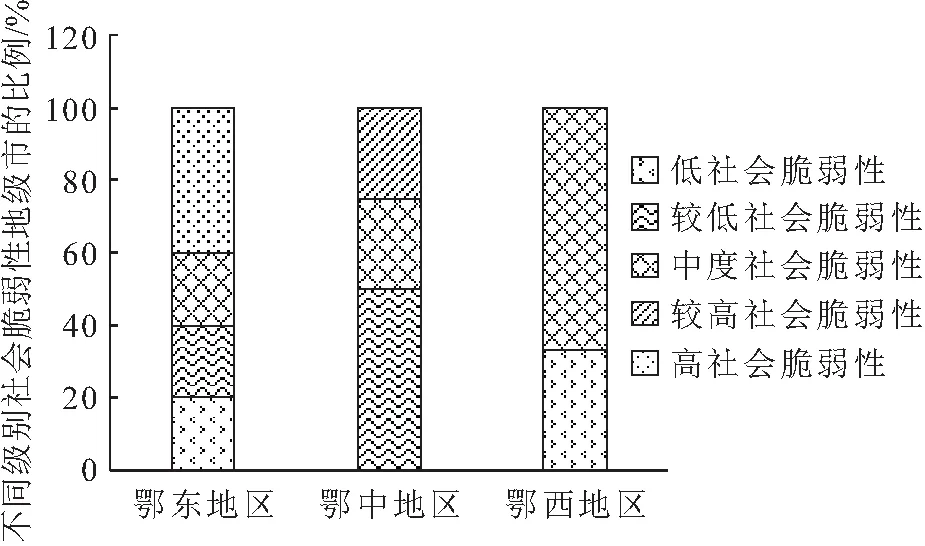
图2 鄂东、中、西部地区不同级别自然灾害社会脆弱 性地级市的分布图Fig.2 Distribution map of different levels of social vulnerability to natural disasters in prefectural- level cities in eastern,central and western parts of Hubei Province

湖北省自然灾害社会脆弱性存在显著的“梯度化”空间分异，呈“东高西低”的空间布局，各城市间自然灾害社会脆弱性的差别相对稳定。例如以2016年为例，从湖北省行政区域划分来看，鄂东、鄂中、鄂西所涵盖的地级市自然灾害社会脆弱性指数的平均值分别为2.937、2.737、2.727，呈现鄂东>鄂中>鄂西的空间分异特征，这是因为宜昌市和襄阳市作为省域副中心城市，其经济基础相对雄厚、产业结构水平相对较高、城市化和工业化速度相对较快，在一定程度上推动了鄂西地区的经济社会发展；从湖北省不同级别自然灾害社会脆弱性地级市的分布来看，中度社会脆弱性地级市主要分布于鄂西地区，较低社会脆弱性地级市主要集中在鄂中地区，而高社会脆弱性地级市集中分布于鄂东地区，占比高达40%，见图2；从鄂东、鄂中、鄂西地区内部各级别自然灾害社会脆弱性城市的占比来看，鄂东地区高社会脆弱性城市的占比最高，低社会脆弱性、中度社会脆弱性和较高社会脆弱性城市的分布较为均匀，均占比为20%，鄂中地区的荆门市和孝感市的社会脆弱性较低，随州市和荆州市的社会脆弱性级别分别为中度、较高，鄂西地区中度社会脆弱性城市的占比为66.67%，低社会脆弱性城市的占比为33.33%，见图3。

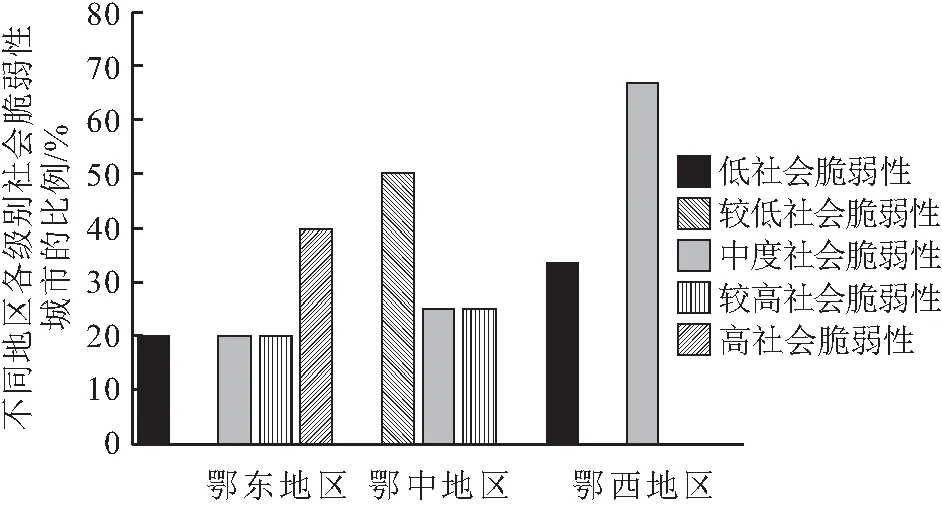
图3 鄂东、中、西部地区内部各级别自然灾害社会脆弱性 城市占比示意图Fig.3 Proportions of cities at all levels of social vulnerability to natural disasters in the east, middle and west of Hubei Province

为了进一步分析湖北省自然灾害社会脆弱性在时空上的变化特征，本文根据计算得到的2001—2016年湖北省各地级市自然灾害社会脆弱性指数，借助ArcGIS，采用自然断点法绘制出2003—2015年湖北省各地级市自然灾害社会脆弱性的时空分布演变图，见图4。

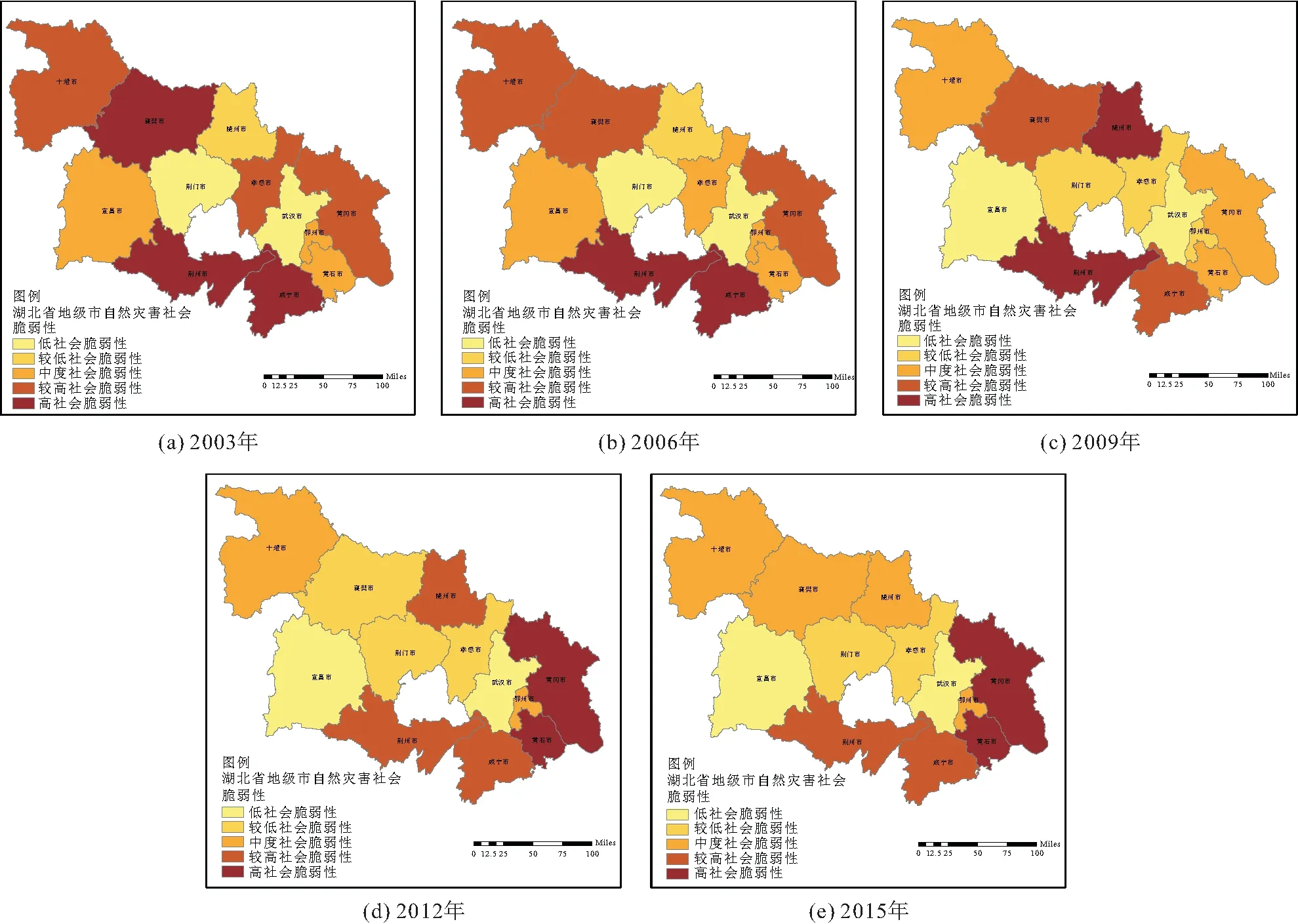
图4 2003—2015年湖北省各地级市自然灾害社会脆弱性的时空分布演变图Fig.4 Temporal and spatial evolution map of social vulnerability to natural disasters of perfecture-level cities in Hubei Province during 2003—2015

由图4可以看出：①2003—2015年间湖北省各地级市自然灾害社会脆弱性水平呈动态变化，除黄冈市和黄石市的自然灾害社会脆弱性明显增加以外，其他城市的社会脆弱性指数均有不同程度的减少，尤其是荆州市和咸宁市，由高社会脆弱性下降为中度社会脆弱性；②2003—2015年间湖北省各地级市自然灾害社会脆弱性水平存在明显的空间分异规律，呈现“东高西低”的空间布局，武汉市一直保持低社会脆弱性，而黄冈市的社会脆弱性逐渐增高，到2015年黄冈市的社会脆弱性最高。

3 结论与建议

受地质条件、气候变化、人类工程活动等因素的影响，湖北省自然灾害愈发频繁，带来了严重的人员伤亡和经济损失，故评估湖北省自然灾害的社会脆弱性对实现防灾减灾抗灾具有现实意义。本文从敏感性和应对能力两个层面来定义自然灾害的社会脆弱性，认为经济社会系统的敏感性和应对能力存在相互影响、相互制约的关系，在此基础上提出了自然灾害社会脆弱性综合评估体系和综合测度模型，并对湖北省12个地级市自然灾害的社会脆弱性进行了实证分析。

(1) 基于文献归纳法，总结出31个自然灾害社会脆弱性评价指标，并利用相关分析和主成分分析对原始指标进行筛选，得到13个具有代表性的相互独立的关键指标，形成了湖北省自然灾害社会脆弱性综合评价指标体系。本文虽然采用了相关分析和主成分分析对原始指标数据进行了客观处理，具备一定的数学理论基础，在一定程度上解决了评价指标体系信息不全或信息重叠的情况，但是由于本文的研究时间跨度较大，研究区域指标数据欠缺，在数据收集和统计上存在一定的困难，直接导致原始评价指标的选取仍存在不可避免的主观性[42]。此外，受限于自然灾害相关指标数据的可获得性，本文仅针对自然灾害的社会脆弱性展开研究，对人类经济社会系统和自然环境的耦合作用考虑欠缺，在今后的研究中需要不断优化评价指标体系，以提高自然灾害社会脆弱性评价的精度。

(2) 基于影响自然灾害社会脆弱性的因素具有模糊性和复杂性的特点，本文选用熵值法对各评价指标进行客观赋权，利用二级模糊综合评价方法来计算湖北省各地级市自然灾害的社会脆弱性指数，并对其展开分析，评价结果表明：从空间层面上看，湖北省自然灾害社会脆弱性存在明显的“梯度化”和“极差化”的空间分异特征，呈现“东高西低”的分布格局，整体上处于中度社会脆弱性的状态；从时间层面上看，湖北省自然灾害社会脆弱性多以波动递减为主，呈现出由“区域大差距、高社会脆弱性向区域小差距、低社会脆弱性格局演变”的趋势。

(3) 通过ArcGIS的可视化处理，可以清晰地看出湖北省自然灾害各级别社会脆弱性的空间格局较为合理，时序演化较为科学，与预期设想和实际的经济社会系统影响大致相符，在一定程度上证明了本文评价方法的合理性和适用性。但是，本文的评价方法与基于模糊层次分析法评价自然灾害社会脆弱性的相关研究相比，在方法运用上存在很大差异[43]，相互之间缺少可比性，无法得知所选评价方法的优劣性，在今后的研究中需要进一步的探索。此外，本文没有针对某种特定类型自然灾害来具体分析湖北省自然灾害的社会脆弱性，也没有对未来湖北省各地级市自然灾害社会脆弱性的发展趋势作出预测[44]，这都将是未来的研究重点和方向。