超声无损检测中声波散射衰减的分数阶导数建模研究
方 俊
(1.南京理工大学紫金学院机械工程学院,江苏 南京 210046;2.河海大学力学与材料学院,江苏 南京 211100)
超声波无损检测技术的基本原理是用人工的方法在被测材料或结构中激发出一定频率的弹性波,以各种不同的频率在材料或结构内部传播并通过仪器接收,通过分析研究所接收的信号,就可以了解材料与结构的力学特性和缺陷分布情况。这些弹性波就是声波,它们在复杂介质内的传播一般都会随距离发生一定的衰减,其中与介质特性有关的两种衰减形式是吸收和散射。由介质分子之间的粘性引起的称为吸收衰减;因碰到另外一种介质组成的障碍物而向不同方向产生发散的现象称为散射衰减,它主要是由介质的非均质性引起的。由于混凝土、岩石等材料内部含有大量的杂质和缺陷,具有高度非均质性,因此实验结果和实地观测表明,在此类介质中声波的散射衰减起主导作用。
研究超声波在混凝土等非均质材料中传播的散射衰减机理和一般规律,对无损检测中分析材料的各项特性有重要的意义。但是声波在非均质材料中的传播过程是非常复杂的,材料内部的缺陷、杂质与孔隙等构成声学界面的数量和空间分布也是随机和多样的,且存在0~4阶之间任意阶频率依赖的衰减现象,现有的以经典力学为基础的整数阶模型只能分析几种整数频率依赖耗散的特殊情况,难以对一般的散射过程进行准确模拟。
文章基于散射衰减规律的经验公式,导出了声波的0-4阶分数阶导数散射衰减模型,该模型能够同时描述任意频率依赖的衰减和因果关系的频散,推动了分数阶导数建模方法在超声无损检测领域中的应用。
1 声波散射建模研究的现状分析
目前国内外对于声波散射衰减的研究大部分是以实验测定的方法为主。散射系数α通常用来表示单位距离内由散射引起的损失能量,上世纪90年代Vary和Mavko等人通过大量实验结果证明该系数α与声波频率ω以及杂质平均尺寸d均存在相关性,并且具体形式取决于声波波长λ和杂质尺寸d之间的大小关系:

其中DS是通过实验数据拟合得到的参数。由该结论可以看出,声波散射一般存在三种不同的类型:当波长λ远小于杂质尺寸d时,发生的是Diffusion散射,大部分散射能量集中在靠近入射波传播的方向,此时α∝d-1;当波长λ和杂质尺寸d差不多时,发生的是Mie散射或称为共振散射,该散射效应最为明显,是超声无损检测中最常见的散射类型,此时α∝dω2;当波长λ远大于杂质尺寸d时,发生的是Rayleigh散射,这种散射类型较常见于地震波的观测中,此时 α∝d3ω4。
根据以上的观测结果,可以将散射的不同类型表达式总结为一个以频率为变量的幂函数形式:

其中α0是与杂质尺寸d相关的一个参数。显然,当s=0,2,4时,就可以得到(1)式中各项表达式。值得注意的是,Aki和Blair等人后来在实际测量中发现s的值并不总是只能取整数,某些情况下也有可能是0-4中的任何一个非整数,这取决于不同介质的材料属性、杂质尺寸与含量以及波长范围等因素。对于这种复杂介质的任意阶频率依赖散射现象,传统的整数阶偏微分方程并不能准确地加以描述,因而需要发展出新的理论来建立相应的数学物理模型。
分数阶微积分是一个解决这类物理和力学建模难题的有力的数学工具,已被广泛应用于声波吸收衰减、反常扩散等领域。分数阶导数建模的优势在于所需物理参数少,方程形式简单明确;此外,将其转化到频域分析则可以变为幂函数形式,因而非常适合描述任意阶频率依赖的声波衰减现象。一般情况下,描述幂律频率依赖衰减关系的声波方程可写成如下形式:

其中:p代表波的压力,c0代表波速,C为衰减项的系数表示a阶时间分数阶导数,(-Δ)b/2为b阶分数阶拉普拉斯算子。当a=1,b=0时,(3)式简化为经典阻尼波方程;当a=1,b=2时,(3)式简化为热粘性波方程。为了得到任意s阶频率依赖的关系,Caputo令a=s-1,b=2首次得到了时间分数阶声波耗散模型;Szabo给出了卷积形式的衰减项,而陈文等将之写成时间分数阶导数的形式,即a=s+1,b=0。此外,陈文等又引入了空间分数阶导数的衰减项,即a=1,b=s,并给出了分数阶拉普拉斯的新定义。这些声波耗散模型在低频近似的前提下均满足幂律频率衰减关系。
然而,以上这些模型并不总能反映声波在介质中的频散,即声速随频率变化的现象。为保证模型能反映频散,Kelly等[16]提出频率依赖的频散系数 β(ω),使模型满足时间因果关系。此外,Treeby等利用频散方程和低频假设,得到了含空间分数阶导数的声波耗散模型。该模型令方程(3)中a=1,b=s,并在等号左侧另外加入频散项从而同时满足频率衰减关系和时间因果关系。
但是,现有文献的分数阶导数声波衰减模型,描述的都是粘性引起的声吸收衰减,导数阶数的范围在0~2之间。而散射衰减由于物理机制不同,从(2)式可以看出,其阶数范围是0~4,因此分数阶导数的定义就必然需要扩展;除此之外,声波方程的各项参数也将有所变化,比如改成与杂质尺寸d相关的参数。下面首先给出分数阶微积分算子的定义,并将0~2阶的分数阶拉普拉斯算子扩展为0~4阶的分数阶双调和算子。
2 声波建模的数学基础
2.1 定义A:时间分数阶导数算子
时间分数阶导数算子现在应用比较广泛的是Caputo型的定义,其满足的基本形式如下:

其中s为分数阶导数的阶数,n为大于s的最小整数,Γ为欧拉-伽马函数。这里要求φ(t)必须是n阶可微的,另外该定义在建模应用及积分变换中需满足的初始条件是以整数阶微积分的形式给出的,例如当n=1且初始时间为0时,就需要给出φ(0)和φ′(0)作为初始条件。该定义满足傅里叶变换关系:

其中ω为频域变量,Φ是函数φ在频域内对应的函数。从(5)式可以看出,分数阶导数算子可以描述时间域和频域上的幂律依赖现象。
2.2 定义B:分数阶拉普拉斯算子
分数阶拉普拉斯算子是一种空间分数阶微分算子,它是Riesz势的逆算子,可以用来描述科学和工程问题的空间非局部性和幂律行为。一般来说,分数阶拉普拉斯算子应该满足傅里叶变换关系
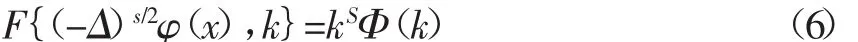
其中(-Δ)s/2为s阶分数阶拉普拉斯算子,它也有多种不同类型的定义。其中比较重要的一种是Chen/Holm形式的定义,其基本表达式如下:

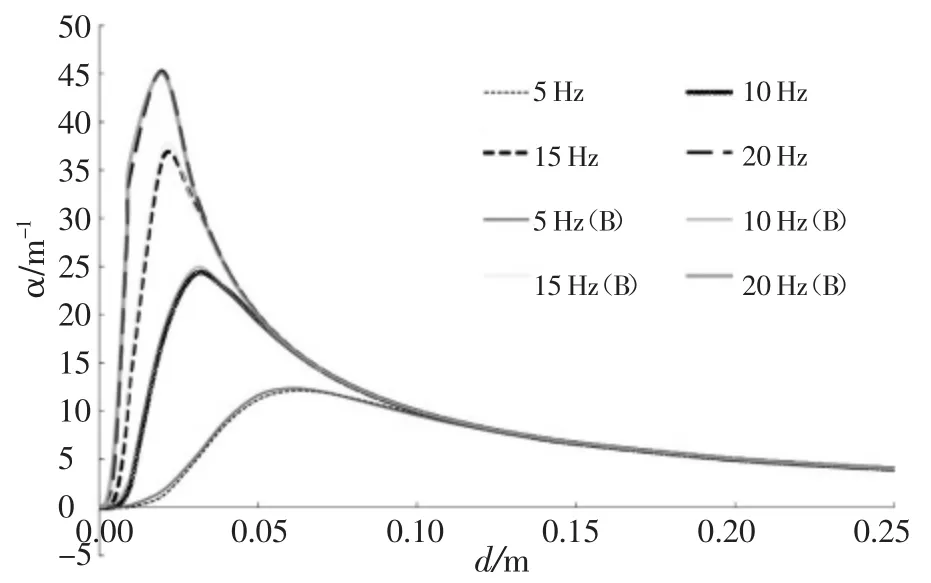
其中0 其中Ω是d维欧氏空间的积分域。可以看到,公式(7)利用Riesz势和拉普拉斯算子的不同结合方式,给出了两种类型的分数阶拉普拉斯显式积分表达式。通过格林第二公式可以证明,Caputo型算子与带边界条件的Riemann-Liouville算子是等价的,这与时间分数阶导数中对应的两类关系是一致的。 将Chen/Holm定义的分数阶拉普拉斯算子(7)式拓展到2~4阶,就可以得到分数阶双调和算子,并给出2种类型的显式积分表达式: 其中2 接下来以散射经验公式(1)为出发点,结合分数阶算子的定义以及声波吸收衰减的建模思路,来建立超声无损检测中声波散射的分数阶导数模型。 考虑到声波散射模型必须既可以描述幂律频率依赖的衰减,又可以描述满足因果关系的频散,根据声波衰减的一般公式(3),给出其包含双衰减项的基本形式: 其中 C1和 C2都是待定的衰减项系数,a,b,p,q为分数阶微积分算子的阶数,其算子定义由第二章给出。这种含空间分数阶导数算子的双衰减项形式是Treeby等首次提出用于描述满足频散关系的声波吸收衰减的。同样可以用这种形式来描述声波的散射衰减。 将(10)式两边同时作时间和空间傅里叶变换,可以得到频域方程: 其中k和ω分别表示复波数和角频率。将(11)式中的复波数拆分成实部与虚部的组合k=β+iα,并将实部和虚部进行分离就可以得到 这里α为散射衰减系数,β为频散系数。方程(12)的第一式是实部满足的条件,与声波的频散相关;第二式是虚部满足的条件,与幂律频率依赖的衰减相关。不失一般性,可以假定(10)式衰减项的第一部分只用于描述幂律衰减,而第二部分只用于描述频散关系。因此,系数C1不应该出现在(12)式的一式中,即 cos(aπ/2)必定为 0,否则会影响频散;同理,系数 C2不应该出现在(12)式的二式中,即 sin(pπ/2)必定为0,否则会影响幂律衰减。由此可以得到系数之间必须满足的关系: 其中m,n都是整数。根据低频假设下的近似关系式 可以将(12)式的虚部简化为 要使散射方程满足(2)式的幂律衰减关系,就必须让(15)式中的系数与之对应,这样就可以得到 接下来将(12)式的实部在低频假设下简化,就可以得到频散系数β的表达式 由于该等式必须满足基于因果关系的Kramers-Kronig频散关系式: 这样就可以得到能同时满足幂律衰减关系和频散关系的声波散射模型的通用公式: 其中0 该方程与Treeby和Cox提出的双衰减项声波耗散模型在形式上是一致的,主要区别在于空间分数阶导数算子的定义不同,并且这里s的取值范围是0-4。此外,该散射模型系数的物理意义也不一样,这里的α0是与杂质尺寸d相关的参数。 上述声波散射衰减模型中,分数阶微积分算子的阶数s,即散射衰减经验公式(1)中幂律指数s的物理意义。由于声波在含杂质的非均质介质中传播时的s取决于声波波长λ和杂质尺寸d之间的大小关系,根据(1)式将其总结为: 其中μ=d/λ表示的是杂质平均尺寸与声波波长之比;b0是当发生Mie散射或共振散射时(d≈λ),μ的具体值。考虑到μ的值实际上应该是一个连续的变量(0,+∞),那么从宏观物理角度来说,s的值也应该是一个连续的变量,而不是“跃迁式”变量。那么为了满足(22)式,幂指数s的一种可能的表达式可以写成 显然,该式满足(1)式的基本关系,但是否有效还需要其他理论或实验的验证。为了与现有散射模型作比较,首先需要写出衰减系数α的精确表达式。将(23)式代入(2)式中并考虑到 λ=c0/ω,就可以求得此时包含杂质尺寸d和波频率ω的衰减系数表达式: 然后将该公式与Blair在上世纪90年代提出的同样包含参数d和ω的散射模型作比较。Blair[8]指出衰减系数α应该满足表达式: 其中CS和kS均为常系数,d表示散射体的平均尺寸,ωd表示特征频率(固定值),仅取决于散射体的固有属性。表达式(25)主要是基于岩石中的地震波散射衰减实验数据得到的,但也被证实同样适用于金属、混凝土或其他非均质材料中的超声波散射衰减。这个现象表明,虽然一般金属等材料中的杂质尺寸要明显小于大多数岩石中的散射体尺寸,但散射本身是一种与尺度无关的现象,其衰减系数的大小主要取决于波长与散射体尺寸之间的比值,而这一结论与所提出的散射衰减模型是一致的。 为了比较两种散射模型中的衰减系数表达式,并讨论杂质尺寸d和频率ω对衰减系数α的影响,通过图形对比了不同波频率下(分别为5Hz、10Hz、15 Hz和 20 Hz)散射衰减公式(24)和(25)中 α 和 d之间的关系。为了使计算简化,假设DS=CS=1,c0=1且根据Blair模型的设定ks=0.23,那么当模型(24)式中的b0=1/4π时,它与模型(25)式是基本一致的,如图1所示: 图1 两种不同模型中散射衰减系数α在不同频率下随杂质尺寸d的变化趋势 从图1可以看出,频率ω的值越大,衰减系数α的峰值就会随之增大;当散射体的平均尺寸d与波长λ近似相等时(d≈πλ),一定频率下的衰减系数α就能达到其最大值。这说明当介质的散射体尺寸和波长大小近似时,声波的散射衰减系数会变得更大,也就是说Mie散射或共振散射是非均匀介质中散射效应最为明显的类型,这一结论也与经验或实验观测结果相一致。以上讨论中,对两个模型参数的取值是b0=1/4π且ks=0.23;而如果选取b0=1/2π且k s=0.4,两者描绘的曲线也仍然是一致的。事实上只要在两个模型中选取适当的参数,它们的衰减系数表达式就是等价的。这也从侧面验证了散射衰减的幂指数表达式(23)的准确性。 文章基于对声波散射的经验公式,从频域分析导出了声波在非均质材料中传播的0-4阶频率依赖散射衰减模型,并给出了含双衰减项的通用公式(20),该模型能同时满足幂律频率依赖的衰减和因果关系的频散。当该通用模型取具体的参数值时,又可以得到与现有声波吸收衰减模型形式上非常相似的分数阶导数散射衰减模型。另一方面,文章又进一步给出了幂指数一种可能的表达式(23),并由此构建了包含杂质参数d和波频率ω的散射衰减系数α的一个新模型(24)。为了验证这个模型,我们将其与现有的Blair模型进行了比较。通过描绘的曲线可以看出,两个模型结果是高度一致的。这就明确了上述声波散射模型通用公式(20)中的分数阶微积分算子阶数s的物理意义,为用模型定量分析超声无损检测中的散射规律提供了一定的理论依据,而且这些工作可以进一步推广到涉及声波衰减的其他领域,例如地震勘探中地震波在多孔岩层中的衰减、医学超声成像、水下沉积物的声波勘测等。
2.3 定义C(新定义):分数阶双调和算子

3 声波的分数阶导数散射衰减通用模型
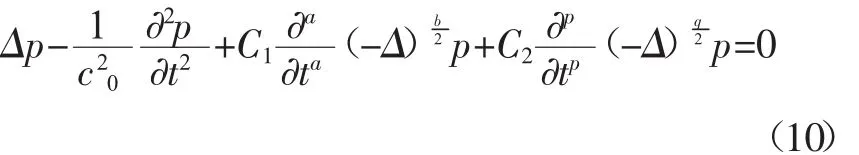
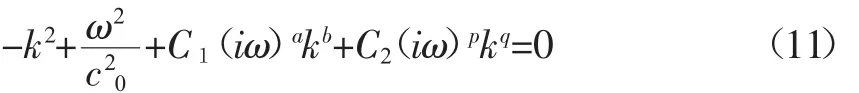



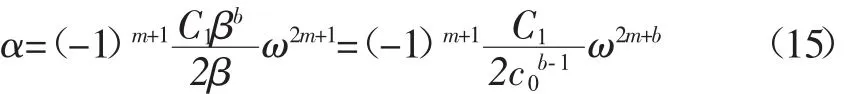

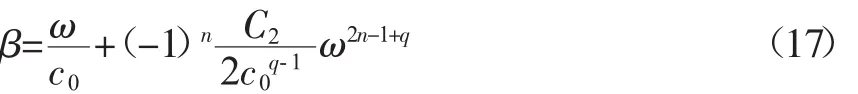

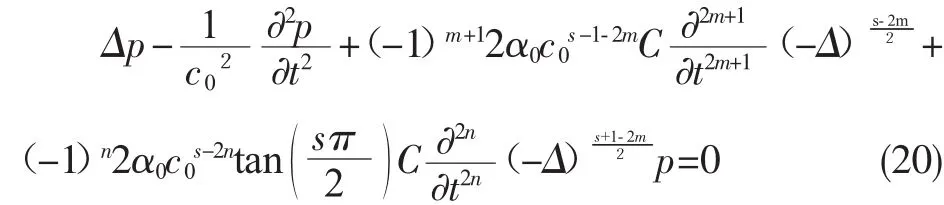

4 散射衰减的幂指数表达式


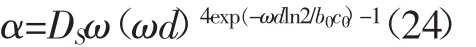
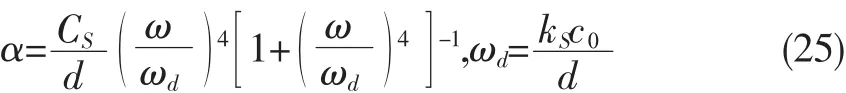
5 结 语

