拱箔成型工艺对箔片轴承性能影响的仿真分析

李昊,耿海鹏,孙岩桦,唐思训,齐垒,虞烈

(西安交通大学机械结构强度与振动国家重点实验室,710049,西安)

弹性箔片动压气体轴承作为一种在高速、高温条件下具有极好稳定性的柔性轴承[1-2],已经在高速轻载旋转机械中得到了广泛的应用[3-4]。弹性箔片动压气体轴承主要由顶层箔片、底层支承及轴承座构成。顶层箔片与轴颈形成摩擦副,目前对于顶层箔片的研究主要集中在箔片材料与固体涂层方面[5]。箔片轴承弹性效果主要由底层支承提供,为达到不同的支承效果,研究人员已经设计出了多种不同结构的底层支承,如拱箔型[6]、多层拱箔型[7]、金属橡胶型[8]、压缩弹簧型[9]、多层鼓泡型[10]等,但目前应用最为广泛的仍是采用拱箔作为底层支承的箔片轴承。因此,如何建立符合实际的拱箔结构数学物理模型就成为了当前研究的热点。

早在1975年,Walowit等就根据拱箔几何结构推导载荷挠度关系式,率先给出了单拱箔片的柔度计算公式[11]。1983年,Heshmat在Walowit载荷挠度关系式的基础上,通过忽略相邻波纹间的弯曲效应建立了等效弹性模型,并给出了与箔片轴承气弹耦合求解流程[12],这一模型应用最为广泛,Peng等的研究结果也为这一模型的正确性提供了佐证[13]。1999年,Iordanoff引入拱箔与顶层箔片间的库伦摩擦力模型[14],徐方程在这一基础上,基于有限元法,建立拱箔型气体径向轴承箔片结构的库伦摩擦模型[15]。

在采用上述模型进行弹性箔片轴承性能计算时,通常假设拱箔为理想状态,即拱箔具有均匀厚度分布及几何型线[16]。这种假设能够为数值计算带来方便,但并不符合拱箔的实际加工过程,同时也没有文献提及拱箔成型工艺对箔片轴承性能的影响。因此,本文将对比理想拱箔与3种典型拱箔成型工艺下弹性箔片动压气体轴承的静、动态性能,通过计算分析,为箔片轴承拱箔的成型工艺提供理论指导。

1 理论分析

1.1 箔片轴承计算模型

图1为进行箔片轴承性能计算时常用的箔片轴承结构形式,主要由顶层箔片、拱箔和轴承座组成[17]。顶层箔片与轴颈形成摩擦副配对,通过气体介质在楔形空间形成的动压效果实现对转子的支承。轴承服役过程中,底层拱箔在压力作用下发生弹性变形,实现柔性支承。

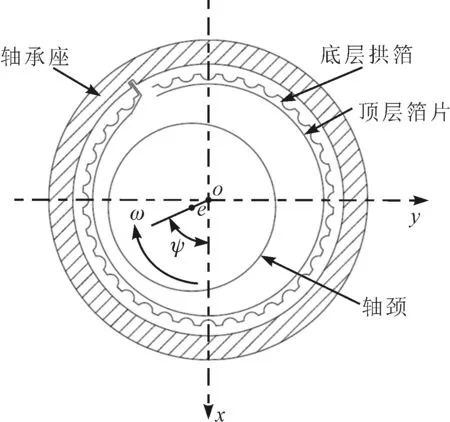
图1 弹性箔片动压气体轴承结构

以轴承中心为原点o,建立右手笛卡尔坐标系如图1所示,其中以竖直向下为x轴正方向,水平向右为y轴正方向,轴承宽度方向即垂直纸面向内为z轴正方向。当箔片轴承在常温常压下服役时,其润滑情况可以使用雷诺方程描述[12]

(1)

式中:x和z分别为轴承的周向和轴向;h为气膜厚度;μ为气体动力学黏度;ρ为气体密度;p为气膜压力;U为轴颈表面旋转线速度。

式(1)只考虑摩擦副的楔形效应,忽略表面伸缩效应及挤压效应,这种简化形式广泛应用于高速轻载箔片轴承的性能计算中。

为方便计算,将雷诺方程转换至柱坐标系,同时结合理性气体状态方程,将雷诺方程简化为无量纲形式

(2)

无量纲规则如下

x=Rφ;z=Rλ;U=ωR

式中:Pa为环境压力,计算中取值为1个标准大气压;C为名义间隙;R为轴承半径;H为无量纲气膜厚度,可以使用下式描述

H=1+εcos(φ+ψ)+wt

(3)

其中ε=e/C表示轴颈相对于轴承的偏心率,ψ为转子偏位角,wt为弹性箔片在气体动压效果下发生弹性变形的无量纲形式,数学描述如下[12]

(4)

其中l0为拱箔半波纹跨度,s为单位波纹宽度,v为底层拱箔材料泊松比,E为底层拱箔材料弹性模量,tb为底层拱箔材料厚度,α为拱箔柔度,S为拱箔无量纲柔度。

1.2 拱箔成型工艺模型

如图2所示,箔片轴承中底层拱箔的成型工艺通常为冷压成型,即将箔片置于凸模与凹模间,通过对模具施加一定载荷,使箔片发生塑性变形,形成拱箔[18]。

图2 拱箔冷压成型示意图

图3为理想拱箔结构,传统分析方法是将拱箔的厚度及型线视为均匀的,并由式(4)获得拱箔在一定压力载荷作用下的变形值,进而计算轴承性能。在实际拱箔压制过程中,由最小阻力定律可知压力会造成金属材料塑性流动,进而导致箔片厚度减薄及型线不均匀,因此在拱箔柔度计算时,使用均匀厚度及型线的假设会造成一定的误差。

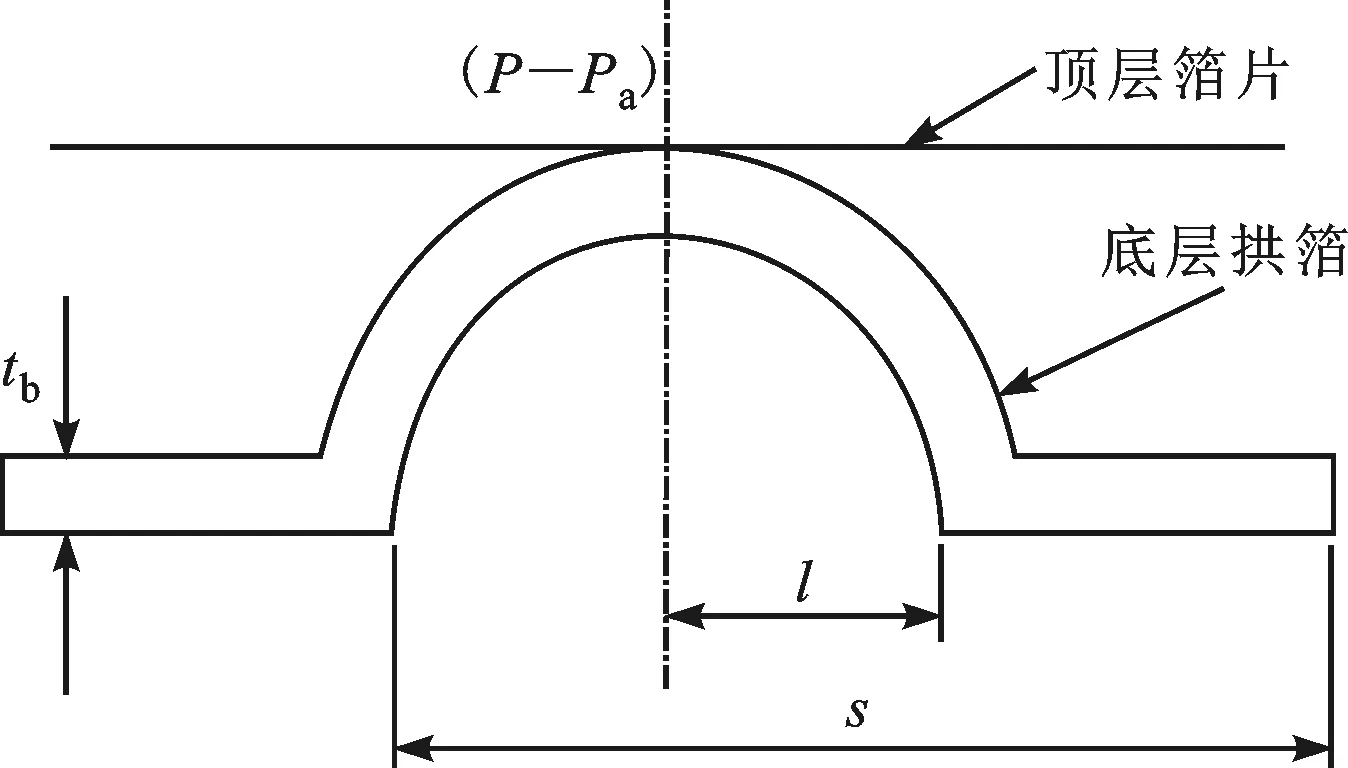
图3 理想拱箔结构示意图

2 数值计算

本文首先建立拱箔冷压成型工艺的有限元模型,获取不同工艺条件下,箔片成型后的结构参数,然后进行不同拱箔参数下箔片轴承的性能计算。

箔片轴承气膜压力控制方程为二阶非线性偏微分方程,无法求出解析解,因此本文将采用二阶中心差分法对式(2)中的气膜压力进行求解,具体差分格式本文不做详细介绍。计算过程中,首先给定气膜的初始厚度,通过式(2)计算得到各节点气膜压力,使用式(4)得到的箔片变形值修正气膜厚度,并将修正后的气膜厚度代入式(2),重复上述过程,直到计算结果满足收敛要求。数学描述为

(5)

式中:∑Pi表示第i次迭代所有节点气膜压力的代数和;∑Pi-1表示第i-1次迭代所有节点气膜压力的代数和;δ表示收敛条件,通常取10-5即可满足计算精度要求。

在描述箔片轴承性能时,通常使用承载力作为静特性指标,在获得气膜压力分布后,按照式(6)积分,即可获得箔片轴承承载力

(6)

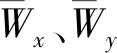
(7)

将式(7)和式(1)联立求解,即可得到用于表征箔片轴承稳定性的的刚度系数、阻尼系数如下

(8)

(9)

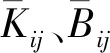
通过上述分析,可以整理得到本文不同拱箔成型工艺下箔片轴承性能计算的流程,如图4所示。

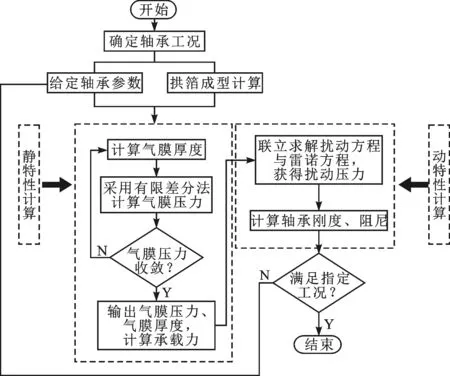
图4 箔片轴承求解流程图

3 仿真结果及分析

为验证本文所述数学模型与计算程序的正确性,使用本文所述模型计算了理想拱箔支承下(式(4)所示无量纲柔度S=1)箔片轴承的性能,并与文献[12]进行了对比(见表1),可以看出本文计算结果与文献结果较好吻合。

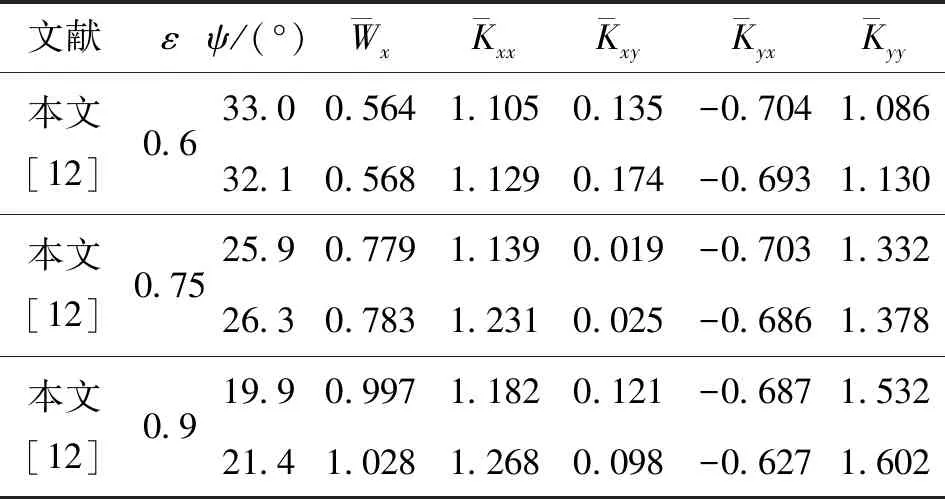
表1 理想拱箔支承下箔片轴承性能计算结果

注:计算中L/R=2.0,Λ=1.0,S=1.0。

表2给出了拱箔冷压成型的工艺参数。拱箔材料采用Inconel x-750,分别使用3种加工工艺进行拱箔冷压成型,工作方式为凹模固定,待加工箔片置于凹模上侧,凸模向下匀速加载。表3给出了本文分析所用轴承的基本参数。

3.1 拱箔成型分析

图5及图6给出了不同成型工艺下拱箔中线处节点厚度分布曲线及拱箔型线,其中拱箔型线测量值为拱箔各点与固定端的垂直距离。从图中可以看出,经过不同成型工艺的拱箔具有不同的厚度及型线分布。相比于3号,1号和2号工艺获得的拱箔厚度与型线更为均匀,这主要是因为3号工艺中,待加工箔片两端固定,导致金属材料延展阻力增大,进而导致局部应力增大,造成了成型不均匀。1号工艺与2号工艺获得的拱箔成型效果基本相同,说明加载速度对箔片厚度及型线的影响相对较小,因为待加工箔片材料为退火态Inconel x-750,具有极好的塑性,在成型过程中几乎不会发生回弹[20],因此对加载速度不敏感。

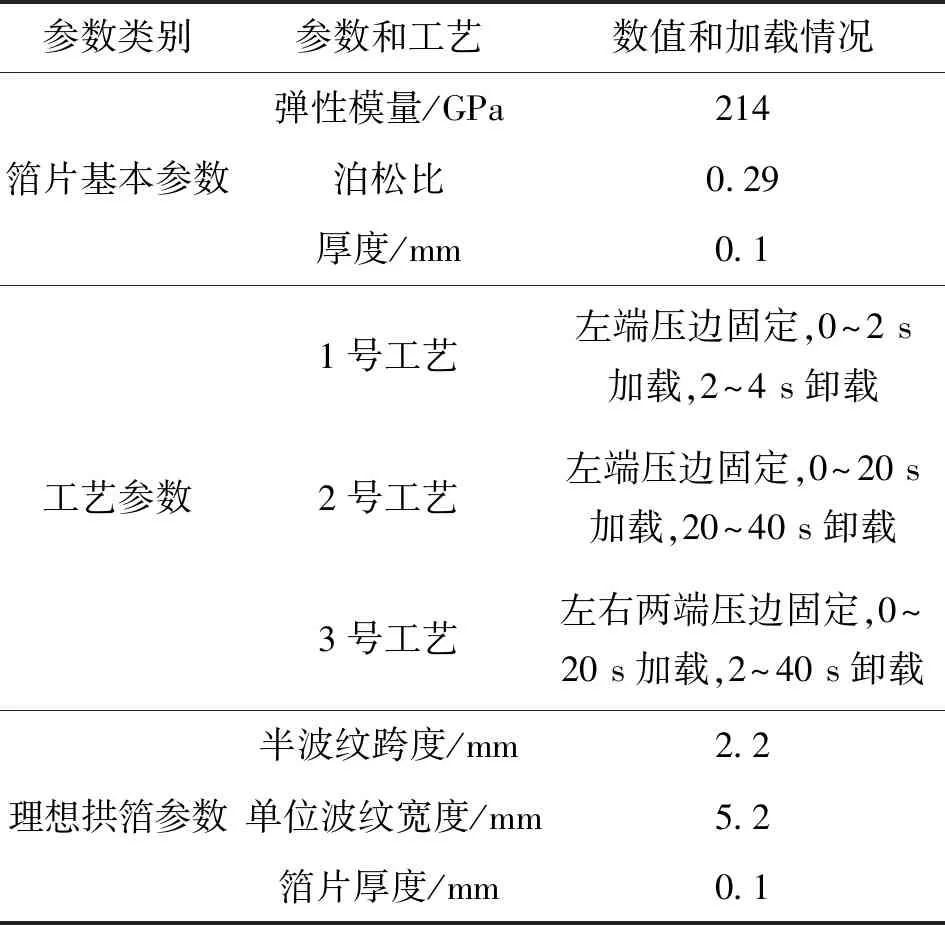
表2 拱箔冷压成型工艺参数(Inconel x-750)

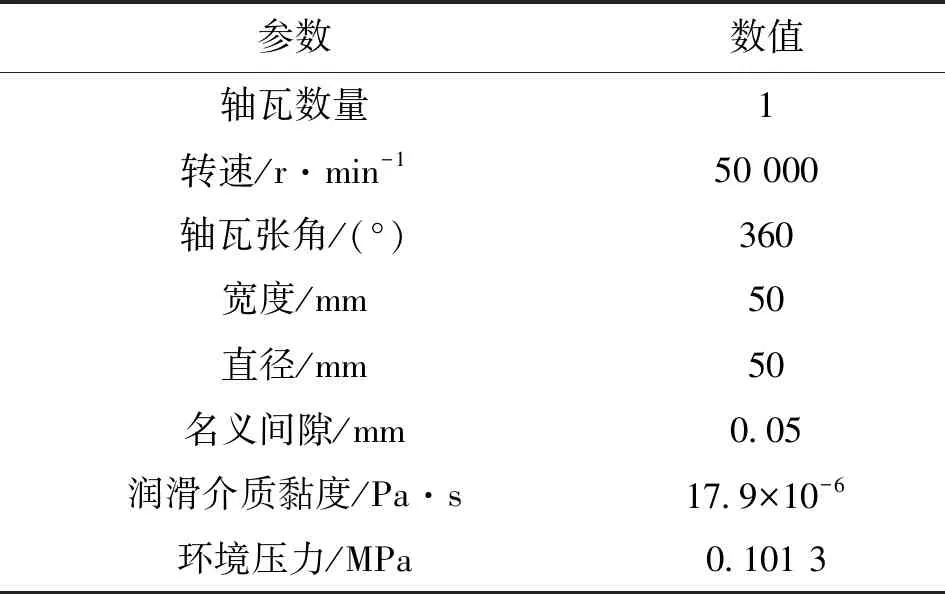
表3 箔片轴承基本参数

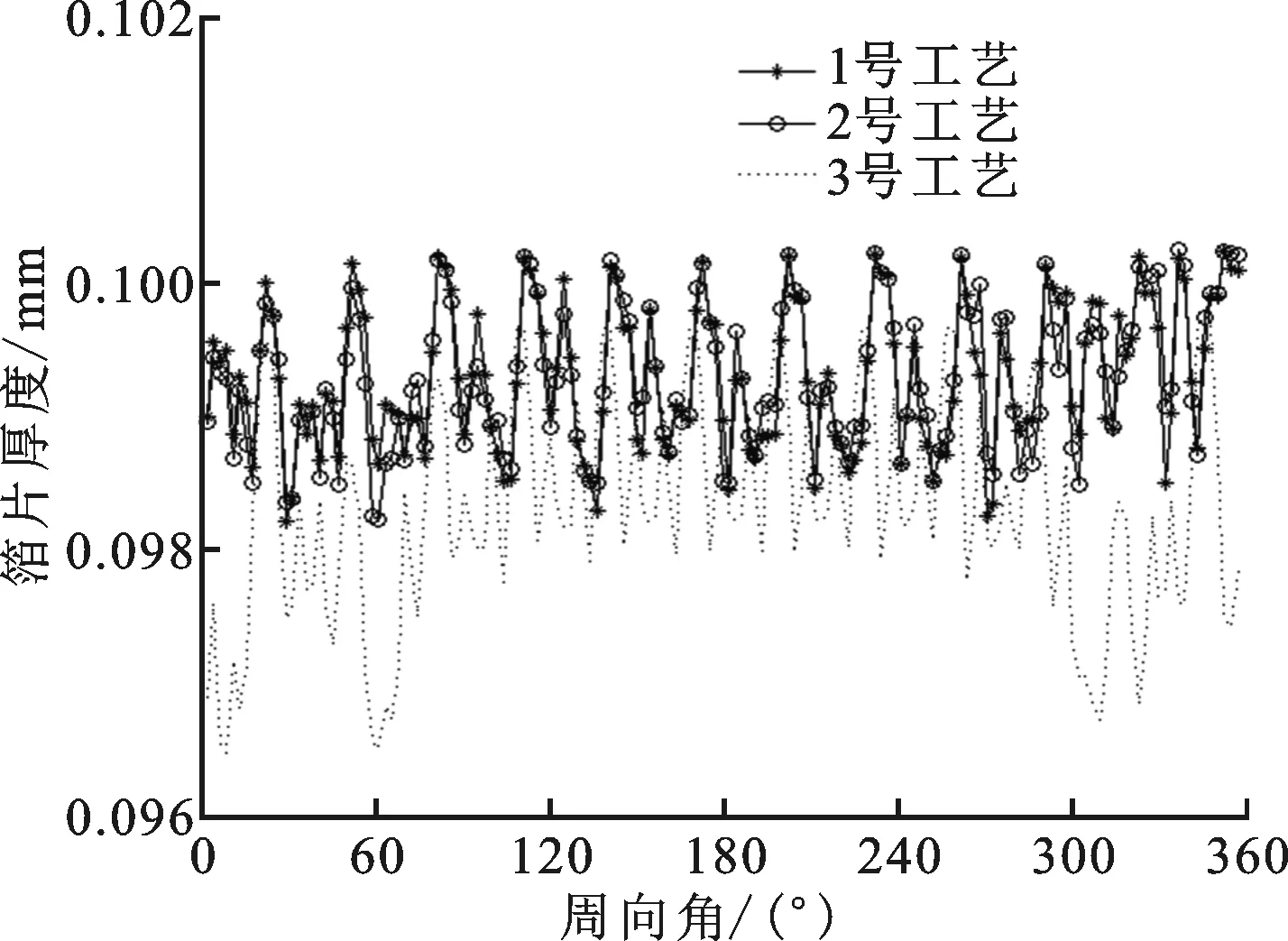
图5 不同成型工艺下的拱箔厚度分布

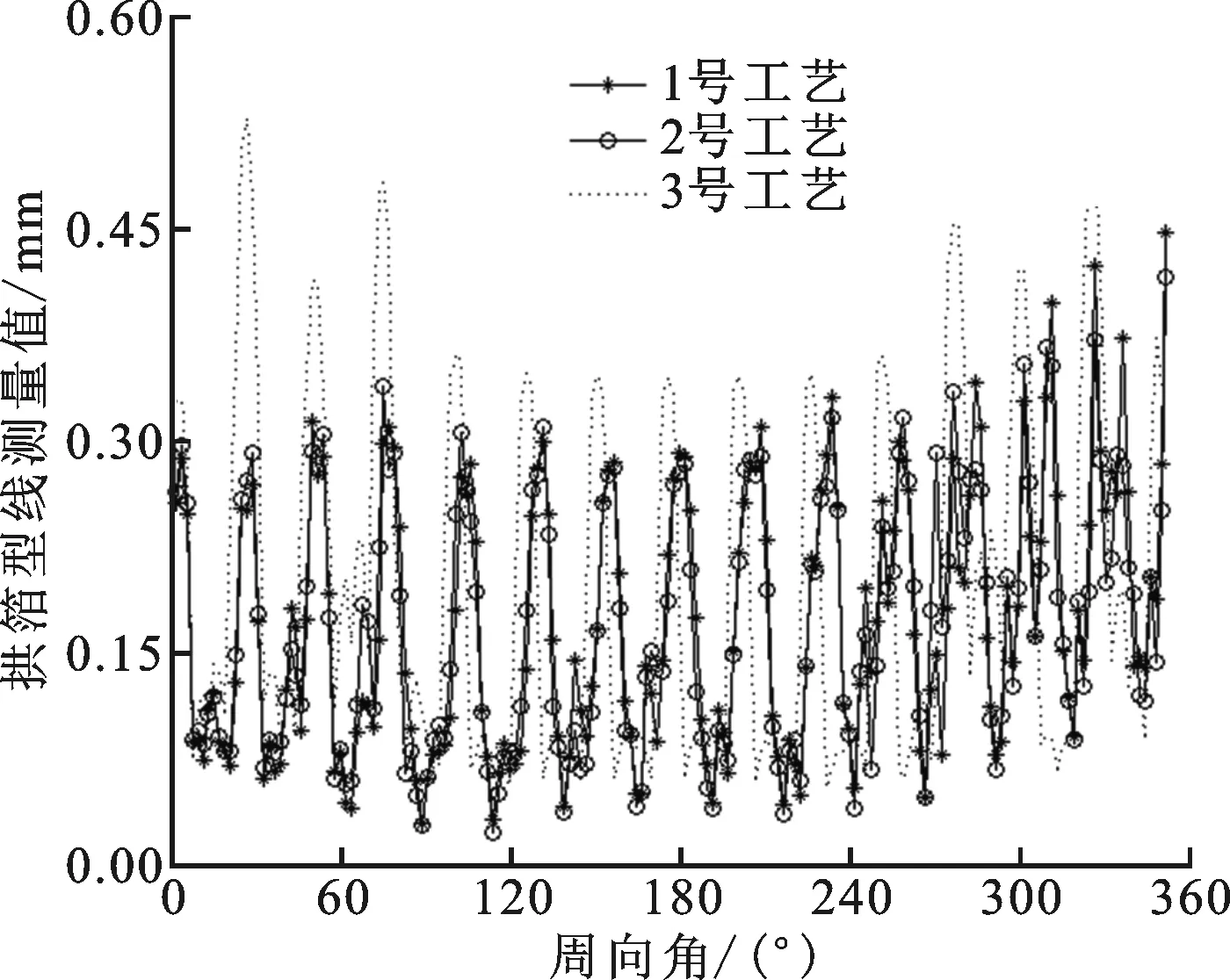
图6 不同成型工艺下的拱箔型线

3.2 承载力分析

图7给出不同拱箔成型工艺下,箔片轴承承载力与偏心率的关系。从图中可以看出,采用不同拱箔加工工艺的箔片轴承,其承载力均低于具有理想拱箔参数的箔片轴承,这也说明在进行箔片轴承设计制造时需要考虑拱箔成型因素。不同拱箔成型工艺下,箔片轴承的承载能力也不同,1号工艺与2号工艺加工出的拱箔的承载能力优于3号工艺加工出的拱箔,如图5所示,1号工艺与2号工艺获得的拱箔厚度与型线都更均匀。在大偏心率(即重载)条件下,2号工艺相比于3号工艺,可以使箔片轴承承载力提高约3%～5%,说明了研究拱箔成型工艺的重要性。

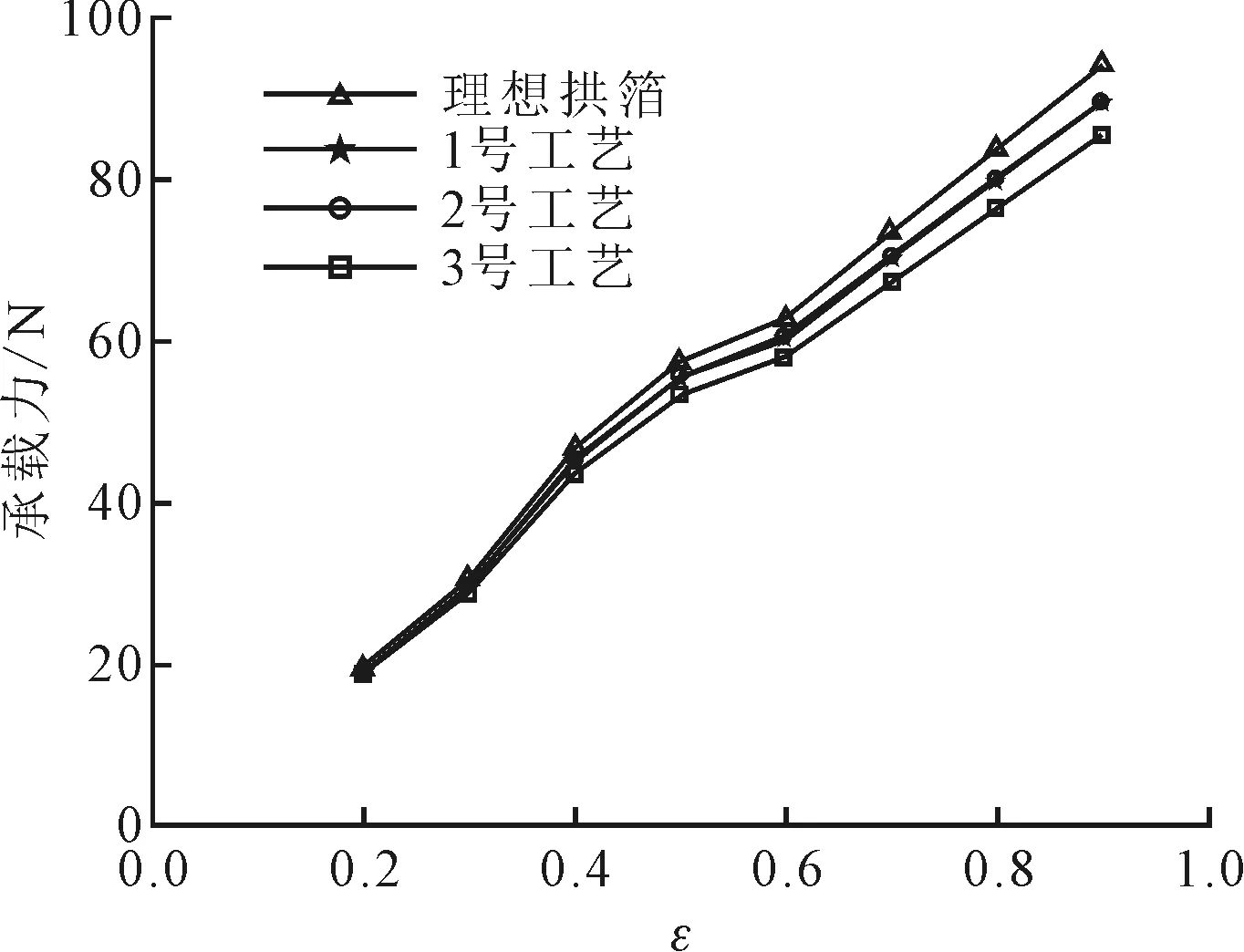
图7 轴承承载力与偏心率的关系曲线

3.3 动力学特性分析

当ε=0.8时,不同拱箔成型工艺下,箔片轴承的刚度系数及阻尼系数见图8和图9。可以看出,3种拱箔成型工艺下的箔片轴承刚度系数均低于具有理想拱箔参数的箔片轴承,同时2号工艺的刚度系数略高于1号工艺的,3号工艺的刚度系数最低。阻尼系数的变化趋势与刚度系数类似。相比于3号工艺,2号工艺可以使主承载方向的刚度系数及阻尼系数分别提高5%及2%,说明拱箔成型加工时厚度及型线的均匀对于箔片轴承的稳定性是十分有益的。

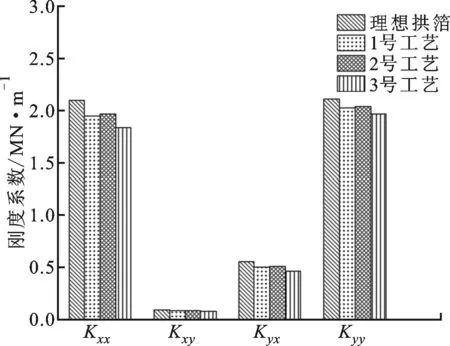
图8 不同拱箔成型工艺下轴承刚度系数

图9 不同拱箔成型工艺下轴承阻尼系数

4 结 论

本文分析了不同拱箔成型工艺对箔片轴承静、动特性的影响,主要结论如下。

(1)拱箔的成型工艺对箔片轴承承载力构成一定影响。不同成型工艺加工出的拱箔支承的箔片轴承承载力均低于理想拱箔支承的箔片轴承,主要是由于拱箔实际加工中,会不可避免地出现箔片厚度减薄、型线不均匀等现象。因此,可以使拱箔获得更加均匀厚度及型线的成型工艺在承载力方面有更好的表现。

(2)在拱箔冷压成型中,采用一端固定的箔片安装方式获得的拱箔成型效果优于采用两端固定的箔片安装方式。对于Inconel x-750这类塑性极好的箔片材料,成型中加载与卸载速度对成型效果的影响较小。

(3)拱箔的成型工艺对箔片轴承动特性构成一定影响。分析结果表明,厚度与型线更为均匀的拱箔支承的箔片轴承稳定性更高。

(4)综上,本文认为在拱箔的冷压成型过程中,最优的工艺为箔片一端压边固定、一端自由,模具加载与卸载速度适中即可,无须刻意放慢加载与卸载速度,这一结论对提高拱箔加工效率及加工质量是很有意义的。