异构无人系统群协同作战任务规划方法

马 硕,马亚平

(国防大学,北京 100091)

随着智能控制技术的发展,无人机(UAV)、无人水下航行器(UUV)、无人水面艇(USV)、无人地面车(UGV)等新型无人智能作战系统(统称UxV)将成为未来战争颠覆性的武器装备。无人系统发展初期,各领域、各部门根据自身需求,发展了种类、数量众多的专用无人装备[1],但随着现代战争复杂程度日益增加,由多类型异构无人系统组成“作战群”,实现跨域协同联合作战已成为重要的发展趋势[2],依靠传统的人工任务筹划手段或各型无人系统专用的任务规划工具已不能满足作战需求,因此需要研究合理的任务规划方法,对不同隶属部门、不同类型的无人系统集群协同作战进行统一管理。目前多无人系统协同任务规划问题解决方法主要分为线性规划模型[3]、约束满足问题模型[4]、启发式方法[5]、智能进化算法[6]等。遗传算法能够在有限的时间内获得相对较好的可行解,在基于遗传算法任务规划的建模、遗传操作等方面开展了较多的研究[7-8]。但目前大多数研究工作与具体应用领域相关,如UAV察打任务[9-12]、UUV水下搜索任务[13]、任务载荷投送[14-15]等,无人系统种类功能、作战任务类型以及数量相对较少,无人系统之间的协同关系相对简单,并需要结合特定领域知识开展有针对性地建模和求解算法设计,因此限制了任务规划方法的应用范围。

异构无人系统协同任务规划相对于单无人系统,任务类型、资源、数量以及任务协同复杂度均有显著增加,协同作战任务的建模和大规模问题的高效求解方法是需要解决的关键问题。本文针对多类型无人系统集群全局任务规划问题,提出一种基于遗传算法的异构无人系统多目标协同任务规划方法HMMOGA(Heterogeneous Multi-UxVs Multi-objective Genetic Algorithm),该方法将任务联盟及对应的任务序列作为染色体个体编码,通过任务联盟之间的变换实现交叉算子,并设计了任务联盟和任务序列的变异方法。

1 无人系统群协同作战任务规划模型

1.1 基本符号定义

无人系统:V={v1,…,vn}表示无人系统平台集合,其中n为平台的个数。

任务载荷:无人系统搭载的任务载荷按是否可重复使用分为两类。例如,武器载荷(导弹、鱼雷等)属于消耗型载荷,而传感器载荷在任务过程中可重复使用,属于非消耗型;每个无人系统可以搭载若干种任务载荷。任务载荷集合统一表示为S={s1,…,sj}。

作战任务:TASK={t1,…,tz},表示作战任务TASK由z个子任务构成。

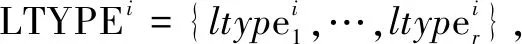
任务联盟:任务联盟(Task Coalition,TC)是一个能够满足给定任务TASK载荷需求的无人系统集合;最小任务联盟(Simplest Task Coalition)是指能满足任务TASK载荷需求,且种类数量最少的无人系统集合;满足TASK所有子任务要求的任务联盟称为可行联盟。

无人系统任务序列:对无人系统vc∈V,需完成的子任务集合,符号表示为tlc(tlc⊆TASK)。

1.2 作战任务模型

1)模型输入参数

① 任务协同关系

图1 模型输入条件

② 任务需求矩阵REQ

矩阵REQ=[reqij](i=1,2,…,m;j=1,2,…n),描述各项任务对应功能需求映射,矩阵的行表示子任务,列表示任务载荷需求;矩阵元素reqij∈{0,1},1代表任务taski需要第j种任务载荷,反之为0。

③ 无人系统能力矩阵VLOAD

矩阵VLOAD=[vloadij](i=1,2,…,m;j=1,2,…n),描述每个平台对应能力映射,矩阵行表示无人系统,列表示任务载荷,矩阵元素定义与REQ矩阵相同。

图2 任务需求矩阵REQ和无人系统能力矩阵VLOAD示例

定义:VLOAD组合运算。VLOAD矩阵第i个行向量符号表示为vloadi(i=1,2,…,m),行运算为行向量之间对应元素的逻辑或计算,用符号“+”表示,目的是得到满足任务能力需求的无人系统任务联盟。任务联盟TC满足某个任务T能力需求,当且仅当vloadtc中的各个元素均不小于reqt。例如,VLOAD1+VLOAD3=(1 1 1 1 0 1)≥req3和req6,即V1和V3组成的任务联盟可以完成任务T3和T6。

2)数学模型

无人系统群任务规划问题描述为:基于给定的TRG和约束条件下,将无人系统集合中的个体或子集分配给各个子任务,目标是使得任务整体效益最大化。任务效益有多种优化目标:如任务总完成时间最短,系统资源(使用的无人系统种类、数量,或航行总里程)消耗最小等。这些目标往往是相互关联的,多目标优化的解是非劣解集合(Pateto解集),如任务联盟{V1,V4}、{V2,V4}、{V1,V3,V4}都可以完成所有的任务,不同的任务联盟完成任务所需的最小航程和无人系统数量等也不同。优化目标可根据实际作战需要选择,采用总航程作为分析对象时,模型如下所示。

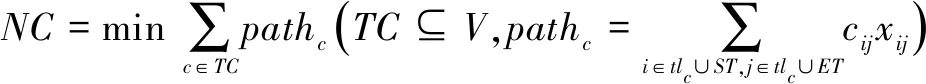
(1)

s.t.ìîíïïïïïïïïïïïïïï∑i∈tlcvloadcxij≥REQj ∀j∈tlc (2)∑i∈tlc∪ETxij=0 j=ST (3)∑j∈tlc∪STxij=0 i=ET (4)∑i∈tlc∪ST,j∈tlcxij≤|Q|-1 ∀Q⊆tlc, |Q|≥2 (5)∑i∈tlc∪STxij≥1 ∀j∈tlc (6)xij=0(i,j∈tlc) ∀TOPOSORT(i)> TOPOSORT(j) (7)

式(1)表示优化目标,即任务联盟TC完成所有任务的总航程最短;式(2)表示每个子任务应满足REQ需求;式(3)、(4)表示ST为任务起点、ET为任务终点;式(5)表示任务路径是无环的;式(6)表示每个子任务都需完成;式(7)表示任务序列应满足拓扑顺序要求。

2 无人系统群协同作战任务规划方法

遗传算法是通用的优化方法,但不同的问题应用领域,约束条件与优化目标不同,需要针对问题域的特点对GA进行改进,设计合理的染色体(解的编码)、遗传算子和遗传进化策略。

2.1 染色体

GA染色体代表问题域的可行解。对任务规划问题P,解空间为所有满足约束条件的无人系统任务分配方案。其中,每个无人系统相应都有一个任务序列,无人系统群的任务序列就构成了任务解矩阵,但直接使用矩阵无法实现选择、交叉、变异等遗传操作,需要根据问题域的特点研究解矩阵的编码方法。根据解矩阵的组成结构,染色体编码由任务联盟和任务序列两个部分构成,如图3所示。

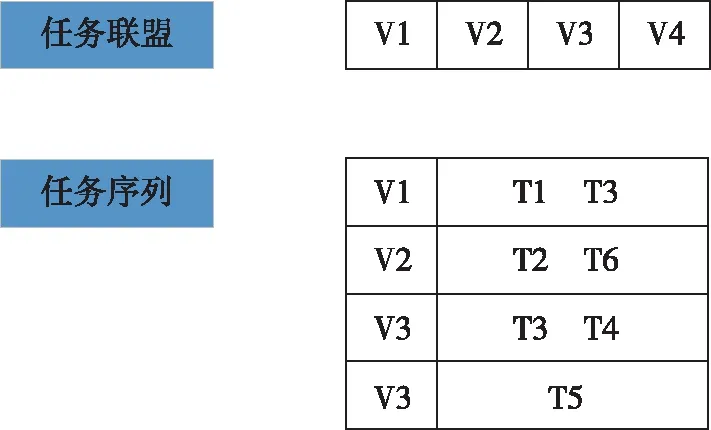
图3 染色体构成示例

2.1.1 任务联盟

通过对VLOAD矩阵组合运算定义,得到满足任务需求的任务联盟。任务联盟求解方法TCCS(Task Coalitions Configuration Solver)伪代码如图4所示。

图4 任务联盟求解方法流程

算法1中,首先确定满足给定数量要求的无人系统任务联盟所有可能组合,在各种组合方式中,选择可行任务联盟存入C,将满足各子任务需求的任务联盟存入D。行13-18在所有满足任务需求条件的任务联盟中,通过合并子集计算最小任务联盟E。最小任务联盟和可行任务联盟示例如图5所示。

图5 最小任务联盟和可行任务联盟示例

2.1.2 任务序列

确定任务联盟集合后,在各个任务联盟中,将子任务分配给无人系统,分别生成各无人系统需要执行的任务序列。无人系统任务序列生成方法VTLS(Vehicle Tasks List Slover)伪代码如图6所示。

图6 无人系统任务序列生成流程

由行1-4得到分别完成各个子任务的任务联盟A,任务联盟是TC的子集。行5-14在A中分别对TC中的各个无人系统,寻找各个无人系统所参与的子任务,并放入tasklist中,最终形成TC中各无人系统任务序列B。表1为任务联盟{V1,V2,V4}随机生成的任务序列示例。

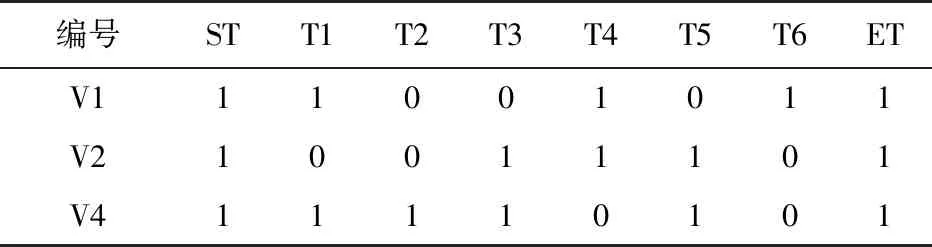
表1 任务联盟{V1,V2,V4}的任务序列

2.1.3 任务序列最短路径

任务具有空间属性,为了实现优化目标,需要计算每个无人系统完成其所负担的任务集合的最短路径。在不考虑任务执行顺序的情况下,该问题即为单旅行商(TSP)问题,但子任务之间存在着时序和逻辑约束关系,因此需要根据TRG约束求满足拓扑顺序条件的最短路径。对一个无人系统v,其长度为M任务序列tlv最短路径表达式为

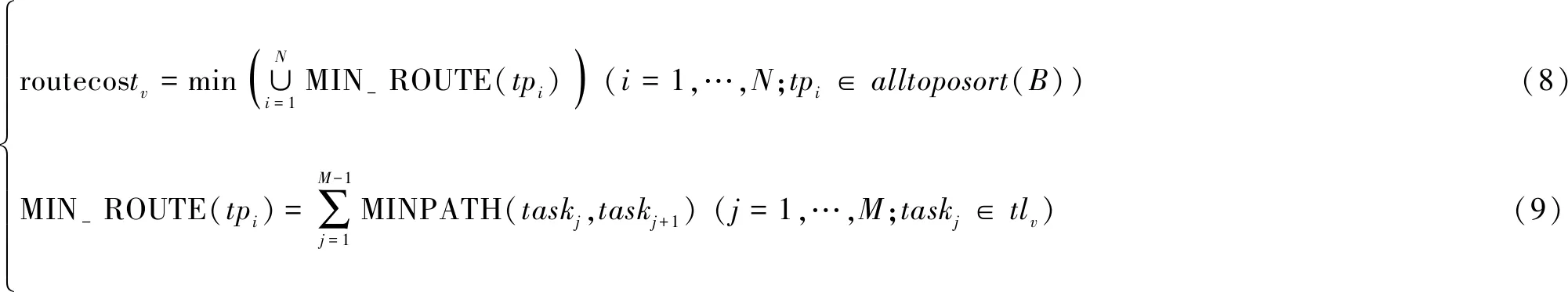
ìîíïïïïïïïïroutecostv=min(∪Ni=1MIN-ROUTE(tpi)) (i=1,…,N;tpi∈alltoposort(B)) (8)MIN-ROUTE(tpi)=∑M-1j=1MINPATH(taskj,taskj+1) (j=1,…,M;taskj∈tlv) (9)

式(8)中,B为TC中各无人系统任务序列,alltoposort(B)为基于TRG对任务序列B拓扑排序后的所有任务序列排列结果,N为排列个数,tpi为第i种拓扑排列,routecost为无人系统执行任务序列所经过的路径代价, MIN-ROUTE(tpi)表示任务序列tpi的最短路径。式(9)为MIN-ROUTE(tpi)的表达式,其中，MINPATH为两个任务之间的最短空间路径。

由于B中可能存在对TRG为偏序的任务集,因此必须考虑所有的拓扑排序结果。式(8)的含义是:在B的所有拓扑排序结果中的最短路径,是无人系统执行任务序列B的最短路径。式(9)表示给定拓扑排序的任务序列最短路径,是前后相邻两个任务之间最短路径之和。按式依次计算得到任务联盟中每个无人系统执行任务的最短路径,以及对应的任务执行顺序。对任务序列{ST,T1,T2,T3,T4,ET}拓扑排序的结果以及相应的路径代价示例如表2所示,最短路径代价是197.9,对应任务序列为{ST,T3,T2,T1,T4,ET}。

表2 拓扑排序结果以及相应路径代价

2.2 遗传算子

2.2.1 选择算子

适应度函数表达式为

(10)

选择算子设计的基本原则是以大概率将适应度强的个体遗传到下一代中。为避免交叉、变异操作对较高适应度染色体个体的破坏,采用最优保存策略,复制一定比例的较高适应度个体到下一代。

2.2.2 交叉算子

交叉算子通过两个同源染色体重组产生新的个体。同源染色体是指满足所有子任务需求的任务联盟中,无人系统种类数相同的两个染色体。对于无人系统数量为SIZE的任务联盟TCsize,交叉算子表达式如下:

CROSS(tci,tcj)=(ntc1,ntc2)

(11)

其中,ntc1、ntc2∈NTC,tci、tcj∈TCsize,NTC是满足{tci∪tcj∩{TCsize-tci-tcj}}∈{TCsize-tci-tcj}的任务联盟集合。交叉算子CROSS首先对两个待交叉的同源染色体任务联盟tci和tcj求并集,之后取除上述两个染色体外所有同源染色体集合{TCsize-tci-tcj}的交集,将计算结果为集合{TCsize-tci-tcj}元素的两个任务联盟ntc1和ntc2,作为交叉后的新任务联盟,并相应产生新的任务序列。交叉算子示例如图7所示。

图7 交叉算子计算示例

2.2.3 变异算子

变异目的是产生新的个体,提高种群的多样性。根据染色体的结构特点,设计两种变异算子。

1)任务联盟变异算子

每个任务联盟对应一组任务序列可行解。在随机产生初始种群阶段,以及在迭代进化过程中,可能会发生部分任务联盟组合缺失,或在同源染色体中所占比例较小的情况,从而导致可行解的搜索空间变小,影响最终优化效果。通过任务联盟变异,可以改善不同任务联盟之间的比例结构,优化搜索空间。设种群中各同源任务联盟的个数为Ni(i=1, …,k,k为任务联盟种类数),任务联盟变异概率表达式为

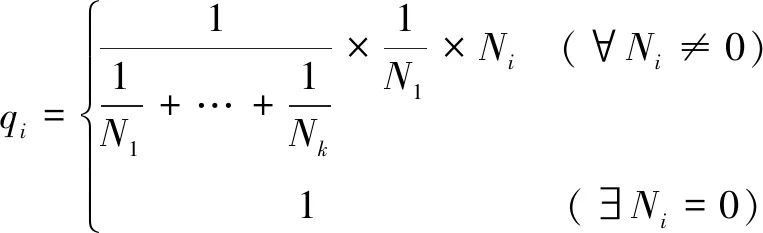
(11)

(i=1, …,k)

式(11)是种群中各同源染色体任务联盟之间的反比例计算方法,即一种任务联盟在种群中所占比例越小,则变异成该任务联盟的概率越大。如果种群中缺少某种任务联盟类型,则变异为该类型任务联盟的概率为1;如果存在多个缺失的任务联盟类型,则随机选取一种任务联盟。表3为任务联盟变异概率示例。

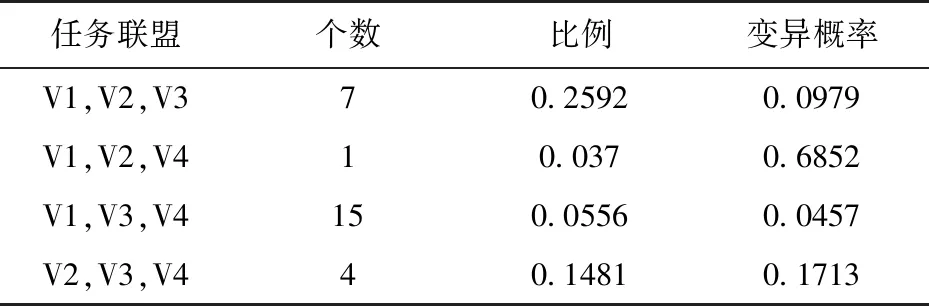
表3 任务联盟变异概率示例

2)任务序列变异算子

对于同一任务联盟,执行不同的任务序列组合,路径代价差别可能较大。另一方面,每个无人系统所分配的任务量可能存在不均的现象,导致有的无人系统工作负载相对较大。任务序列变异算子的作用是在不同无人系统之间进行任务调配,将承担较大任务负载的无人系统任务序列中的任务,部分分配给其他无人系统,以期获得相对较小的路径代价以及相对均衡的任务负载。任务调配方法TAAS(Task Allocations Adjustment Solver)伪代码描述如图8所示。

图8 任务调配方法流程

行4-9在任务负载最大的无人系统v的任务序列中,随机选一个待删除的任务a,如果在不包含v的TC子集任务联盟中,存在可以完成任务a的任务联盟t1,则在完成任务a的原任务联盟任务序列中删除a,并在无人系统任务序列t1中增加任务a。任务序列变异示例见表4、5所示。在表4所示的染色体中,V1任务序列路径代价最大,因此选择一个可删除的任务T5,原T5由V1和V4完成,变异后由V2和V4完成,变异前总路径代价为487,变异后减小为480。

表4 变异前任务序列及路径代价

表5 变异后任务序列及路径代价

2.3 HMMOGA流程

为了得到非劣解集合,HMMOGA方法从无人系统最小任务联盟开始,在不同规模的任务联盟条件下,计算无人系统依次执行任务的最小路径代价(见图9行1)。HMMOGA首先产生初始种群,生成规定数量的染色体。根据算法1和算法2,为每个染色体个体的TC和TL赋随机初值,并计算最短任务路径、总任务路径。种群初始化后,HMMOGA开始迭代进化过程(行9)。在每代种群进化过程中,使用最优保存策略,将一定比例的最高适应度个体直接复制到下一代[16]。

行13-15对当前种群中未被复制的染色体个体按一定的概率进行交叉、变异操作,首先在种群中以随机的方式组成配对个体组,根据设定的交叉概率根据算法3 产生新的TC,并根据TC随机更新TL及其他值。交叉操作完成后,在种群中按设定的变异概率对染色体的TC和TL进行变异操作。HMMOGA方法伪代码流程如图9所示

图9 异构无人系统群多目标任务规划流程

2.4 仿真结果

模型及输入参数同上文实例。遗传算法控制参数设定为:种群个体数目为20,代沟为0.9,最大遗传代数100,交叉概率0.1,任务联盟变异概率0.2,任务序列变异概率0.2。不同种类数量的可行任务联盟执行任务的优化结果见表6所示。

遗传算法迭代计算过程如图10所示, HMMOGA算法能够较快的收敛到最优解。在SIZE=2时,有两种可行任务联盟{V1,V4}和{V2,V4},且约束条件下各自只有一种任务序列组合方式(任务联盟{V2,V4}的任务序列为V2:{T1,T3,T5,T6},V4:{T1, T2,T3,T4,T5},路径代价为428),而在种群初始化时有20个个体,因此最优解在种群随机初始化时就已出现。在本例中,随着无人系统可行任务联盟类型数量的增加,最小路径代价也随之增加,主要原因是增加的无人系统在起始点、终点和任务区之间的累积航行距离有所增加,但更多的无人系统也能使得任务并行执行情况增多(见SIZE为3、4时T5的执行),从而进一步减少总任务执行时间。

图10 HMMOGA迭代优化过程及最优解

3 结束语

根据异构无人系统执行作战任务的特点,提出了任务规划模型,设计了HMMOGA算法解编码方法,以及相应的复制、交叉、变异算子。仿真结果表明,经过迭代遗传变换,HMMOGA方法能够在满足约束关系的前提下,得到相对较好的优化方案(理论上遗传算法不一定得到最优值),实现异构无人系统集群全局任务规划的能力。在此基础上,将路径代价变为关键任务序列时间(即任务最短执行时间取决于执行时间最长的任务序列),可进一步扩展任务执行时间等任务优化目标。后续主要工作是引入任务持续时间等约束,使模型更加贴近实战条件。