双轴模拟式太阳敏感器测试链误差分析及修正
徐晓丹,王建福,种荟萱,高长山,梁鹤,洪帅,吕政欣,孙艳,王春宇,*
1.北京控制工程研究所,北京 100190
2.河南瑞发水电设备有限责任公司,南阳 474550
基于四象限硅光电池[1]的双轴模拟式太阳敏感器(以下简称双轴模太)可实现两轴太阳矢量角的同时测量,容易实现大视场范围内的高精度测量,并具有体积小、质量小、高可靠、易集成等特点,适用于微小卫星的翼板定向、卫星定姿[2]等多种任务,在微小卫星姿轨控系统中具有独特的应用价值。为此,浙江大学[3]、清华大学[4]、北京控制工程研究所[5]和荷兰 TNO-TPD公司[6]等国内外研究机构均进行了相关研究。为进一步提高产品精度,文献[7]分析了双轴模太装配环节中各误差源的影响,为敏感器的误差补偿和性能提升奠定基础[8-9]。目前双轴模太的视场超过了(±60°)×(±60°),精度优于 0.5°[5]。然而,双轴模太基于各象限光生电流间的相对关系实现太阳矢量角的测量,而各象限光生电流测试链路上的不一致,如各象限响应率、各象限光生电流的电压转换、信号放大、A/D转换系数及暗电流等环节存在的偏差,会直接影响各象限光生电流间的相对关系,进而影响双轴模太的测量精度,目前尚未有相关文献对此进行定量分析和有效修正。通常的做法是对测试链路的转换精度及其一致性提出较高要求,从而加重了后处理电路的实现负担。为此,本文基于数值仿真,针对测试链路的影响进行了定量分析,并提出了校准和补偿算法,在不改变测试链路指标的情况下,有效提高了敏感器的测量精度,也为其他多路信号源敏感器的后处理实现提供了参考。
1 双轴模太工作原理
双轴模太采用四象限硅光电池为敏感元件,可实现两轴太阳矢量角的同时测量。四象限硅光电池是在一片正方形硅光电池上光刻出4个独立的同尺寸同面积的光敏象限,编号分别为S1~S4,相互间隔为b。在硅光电池正上方h处设置掩膜板,掩膜板底面光刻有边长为d的正方形通光孔。在不同太阳矢量入射角度下,透过通光孔的太阳光线在硅光电池不同象限的投影光照面积不同,如图1所示。图中,+Xss轴、+Yss轴分别为俯仰轴、偏航轴,α、β分别为俯仰角、偏航角;m、n分别为太阳光线在硅光电池上投影的中心点在 +Xss、+Yss轴方向偏离硅光电池中心点的距离。由几何关系可知,硅光电池各象限受光照面积S1~S4分别为:
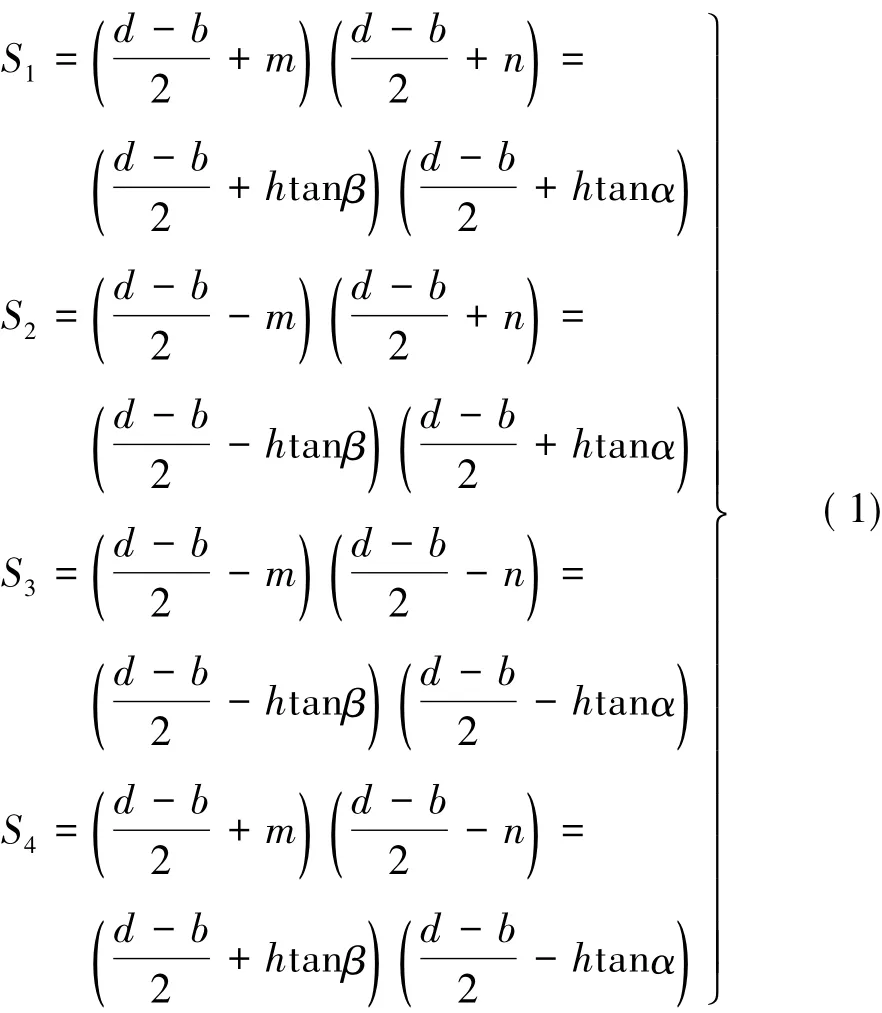
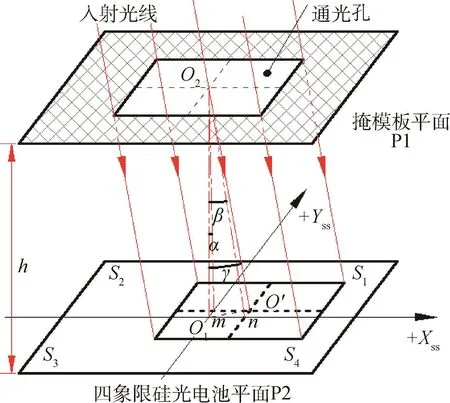
图1 双轴模太工作原理Fig.1 Principle of dual-axial sun sensor
硅光电池各象限光生电流与受光照面积成正
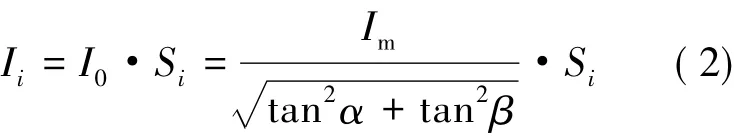
式中:i=1~4,表示硅光电池各光敏象限;I0为硅光电池在该入射角下的响应率,Im为硅光电池在光线垂直入射时的响应率,进而可得:

可知,通过硅电池各象限输出电流的相对关系,可计算出俯仰角α和偏航角β。
2 双轴模太测试链误差分析
双轴模太多用于翼板定向,应用环境极为恶劣,故双轴模太多呈分体式结构,即信号处理电路分体设置于航天器舱内,由此带来测试问题。图2给出了双轴模太的一般测试链路,其中,太阳模拟器配合双轴转台模拟给出双轴模太受双轴矢量角α、β的太阳光照,硅光电池各象限根据光照面积Si(i= 1~4,表示硅光电池各光敏象限,下同)产生相应的光生电流Ii。为弥补太阳模拟器光照强度不足,往往将硅光电池光生电流放大为Ii1。为便于信号采集,将其进行电压转换为Ui1;为提高A/D转换信噪比,进一步进行电压放大为Ui2,经A/D转换为数字量Ui3,并输入处理器,解算出双轴太阳矢量角 α、β。

图2 双轴模太各象限光生电流处理链路Fig.2 Test chain for each quadrant photocurrent of dual-axial sun sensor
理想情况下,各环节中对4个象限信号的处理完全一致,可表示为:
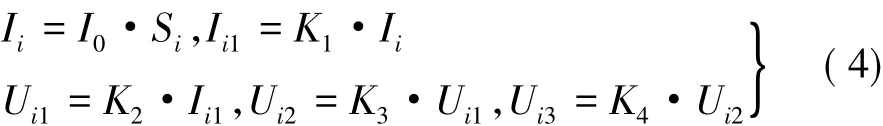
即
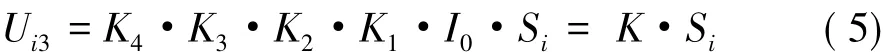
式中:I0为硅光电池象限在该入射角下的响应率;K1为电流放大系数;K2为电压转换系数;K3为电压放大系数;K4为A/D转换系数;K为测试链的综合转换系数,K=I0·K1·K2·K3·K4。则,式(3)转换为:

然而,在实际情况中,各通道之间存在偏差,且含有暗电流信号噪声,对其进行线性化简化,可表示为:

即

式中:Ii0、Ni0为硅光电池第i象限在该入射角下的响应率及暗电流;Ki1、Ni1为通道i的电流放大系数及暗电流;Ki、Ni2为通道i的电压转换系数及暗电流;Ki3、Ni3为通道i的电压放大系数及暗电流;Ki4、Ni4为通道i的A/D转换系数及暗电流;KiS为测试链通道i的综合转换系数;NiS为测试链通道i的综合暗电流。其中,
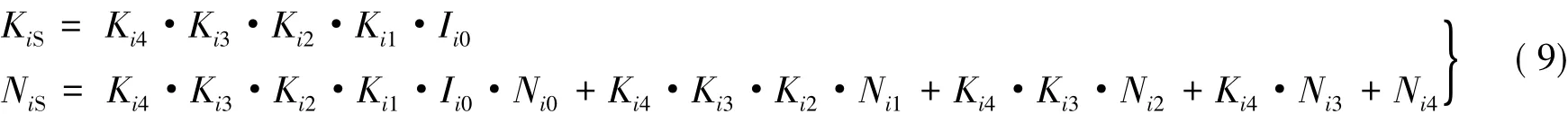
则式(3)转换为:

对比式(6)、式(10)可知,若忽略硅光电池各象限信号测试链路的不一致性及暗电流,将对敏感器的测量精度产生影响。
设 Im=350μA/mm2,(d-b)/(2h)=1.0273,设定各测试链路不一致性为1%、3%、5%,暗电流为1μA、5μA、10μA、30μA、50μA,且双轴视场(±48°) ×( ±48°),并忽略装配及测试其他环节的误差,采用蒙卡仿真方法,可得在不同测试链路不一致性及暗电流指标影响下的双轴模太测量偏差情况,如图3所示(由于α、β轴具有对称性,图中仅给出了单轴的仿真情况)。
图3中,横坐标为测试链暗电流,图中各曲线分别表示测试链不一致性1%、3%、5%,每个测试点处的竖线表示各测试结果的波动(±3σ)。为显示清晰,将不一致性1%和5%的曲线相对3%的曲线沿横轴分别前后偏移1 μA进行显示。由图3可见:
1)随着不一致性及暗电流的增大,双轴模太的测量偏差也逐渐增大,且不一致性造成的影响更为显著;
2)偏差均值、最大值、最小值的波动基本上仅与不一致性有关,且随着各通道不一致性越大,双轴模太测量偏差的波动性(即离散性)越大。
更进一步,图4给出了不同测试链路不一致性及暗电流指标影响下,取得各轴测量偏差峰值点的位置变化(考虑到测量偏差曲面的对称性,图中的角度位置均取绝对值)。由于测量偏差峰值位置波动较大,不具有趋势分析意义,图中仅给出了测量偏差峰值点的平均位置。图中横坐标为测试链暗电流,各曲线分别代表测试链不一致性1%、3%和5%。

图3 测试链路不一致性及暗电流的影响Fig.3 Influence of the inconformity and dark current noise in test chain for each cell quadrant photocurrent on the measurement precision of the sensor

图4 测量偏差峰值位置Fig.4 α and β position for peak of α_err and β_err
举例说明,当不一致性1%,暗电流为10 μA时,由图4(a)(b)可知,双轴模太的α轴测量偏差峰值点的平均位置为|α|=24°、|β|=48°;由图4(c)(d)可知,双轴模太的β轴测量偏差峰值点的平均位置为|α|=48°、|β|=24°。
由此分析可知,对于α轴的测量偏差情况,多在β轴边界位置处的α轴测量偏差最大,而α轴位置多随暗电流增大、不一致性降低而逐渐向边界方向移动;β轴的测量偏差情况与此类似。
3 双轴模太测试链误差修正
由第2节可知,在仿真条件下,要实现0.5°(3σ)的测量精度,需要达到:硅光电池各象限测试链综合不一致性小于1%,暗电流小于30 μA。而由图2可知,双轴模太光生电流需经多个环节依次进行处理,要实现上述链路指标,链路各环节均需达到较高精度,要求较为严苛。
考虑到图2所述各环节均由电子元器件构成,其比例系数及暗电流噪声在一定时间内、一定条件下具有稳定性,故可首先对各通道测试链路进行标定。采用太阳模拟器测得硅光电池象限i响应率Ii0及暗电流Ni0,采用标准信号源测得通道i光生电流的放大、转换、采集环节的放大系数及暗电流Ki1~ Ki4、Ni1~Ni4,由式(9)得到通道i的综合转换系数KiS和综合暗电流NiS,进而由式(10)实现对测试链误差进行修正,从而降低对链路各环节一致性及暗电流噪声指标的需求。
对于某双轴模太,不考虑硅光电池各象限测试链路误差,而仅按照文献[5,7]所述方法对双轴模太装配偏差进行补偿,得到双轴测量误差曲面如图5所示。由图5可知,α轴偏差范围为-1.34°~1.32°,测量精度为 2.05°(3σ);β 轴偏差范围为-1.22°~1.30°,测量精度为 1.94°(3σ),偏差很大。
依据本节提出的测试链修正方法,先对硅光电池各象限测试链进行综合标定,得,

可知,各象限测试链一致性偏差为3%,暗电流为65 μA,其性能指标较差,不能满足双轴模太信号处理需求。
为此,由式(10)对各测试链进行修正,可得修正后的双轴测量误差曲面如图6所示,其α轴偏差 α_err范围为-0.21°~ 0.26°,测量精度为0.28°(3σ);β 轴偏差 β_err 范围为-0.24°~0.29°,测量精度为 0.26°(3σ)。由此可见,相较补偿前,在不改变测试链精度的前提下,双轴模太测量精度仍能得到极大提升。

图5 测试链误差补偿前双轴模太误差曲面Fig.5 Measurement error of sensor without the test chain compensation

图6 测试链误差补偿后双轴模太误差曲面Fig.6 Measurement error of sensor with the test chain compensation
4 结束语
双轴模太测试链路的不一致性及暗电流会改变硅光电池各象限信号的相对关系,从而给双轴模太测量精度造成影响。而本文提出的测试链路误差修正方法,可在保证敏感器测量精度的同时,降低对测试链指标的要求。此外,本文提出的方法,也可在不同测试链路间,特别是对于分体式双轴模太,在地面测试设备及星上线路盒测试链路间的切换过程中发挥重要作用,从而避免了重复测试工作。

