巧用图像法 曲径变坦途

刘福洲

(陕西省岐山县蔡家坡高级中学，陕西 岐山 722405)

图像解题法,它的优势是可以使抽象的物理概念变得更加形象,复杂的物理过程变得直观,从而达到化难为易、化繁为简的目的,特别是一些变速度、变加速度、变力做功等过程,在这些情况下灵活应用图像法往往能起到事半功倍的效果,帮助高中生更好地理解物理概念、物理规律,促使他们更加清晰、简明地分析物理问题、提高解决问题的准确率．下面,笔者就结合具体的教学实例,谈谈图像解题法在高中物理教学中的典型应用．

图1

例1.如图1所示(俯视图),在光滑水平面上竖直固定一根半径为R的竖直圆柱,用长为L的不可伸长细线将光滑小球与圆柱相连．起初,小球位于水平面上并且细线被拉直,现给小球一个垂直于细线的初速度v0,于是,小球开始绕圆柱运动,并将细线缠绕在圆柱上,细线始终在小球滑动的水平面内,问细线全部缠绕在圆柱上需要多长时间?

图2

解析:在每一瞬间,小球均以细线与圆柱的切点为瞬时中心,以未缠绕的细线为半径做圆周运动,如图2,故小球的速度v总是垂直未缠绕的细线,因此,细线的张力对小球不做功,即小球的速度大小不变而方向不断变化．

⋮ ⋮

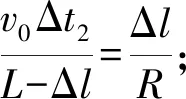
t=Δt1+Δt2+…+Δtn=

图像法:由于细线始终与立柱相切,因此细线转过的角度和过立柱切点的半径转过的角度,以及小球速度方向转过的角度相同．如图所示,设细线从初始位置开始转过的角度θ(小角度),则立柱上细线缠绕的长度为Rθ,同样小球运动的半径就减少Rθ,即L′=L-Rθ,由此可知

角速度与角度是非线性关系,两者的关系图像为曲线,尝试将上式变形可得

图3

例2.蚂蚁离开巢沿直线爬行,它的速度与到蚁巢中心的距离成反比,当蚂蚁爬到距巢中心L1=1m的A点处时,速度是v1=2cm/s,试问:当蚂蚁从A点爬到距巢中心L2=2m的B点所需的时间为多少?

图4

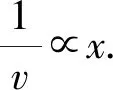
例3.(2014年安徽高考卷第24题)在光滑水平地面上有一凹槽A,中央放一小物块B.物块与左右两边槽壁的距离如图5所示,L为1.0 m,凹槽与物块的质量均为m,两者之间的动摩擦因数μ为0.05.开始时物块静止,凹槽以v0=5 m/s初速度向右运动,设物块与凹槽槽壁碰撞过程中没有能量损失,且碰撞时间不计,g取10 m/s2.求

(1) 物块与凹槽相对静止时的共同速度;

(2) 从凹槽开始运动到两者相对静止物块与右侧槽壁碰撞的次数;

(3) 从凹槽开始运动到两者刚相对静止所经历的时间及该时间内凹槽运动的位移大小.

解析： (1) 设两者间相对静止时速度为v,由动量守恒定律得

mv0=2mv,

解得v=2.5m/s.

(2) 以凹槽A与物块B为系统,假设两者发生碰撞的次数为n,由能量守恒定律得

n=13.

可推知物块与右侧槽壁共发生6次碰撞.

mvi+mui=mvi′+mui′,

解得vi′=ui,ui′=vi(交换速度).

由以上结论可知,i=1,2,3…因此,发生第一次碰撞前,凹槽A与物块B的速度分别为v1、u1,碰撞后速度分别为u1、v1,其他碰撞情况的速度字符表示,以此类推．

整个碰撞过程以及碰撞过程的位移字符表示如图6所示,可得凹槽A发生的总位移为

图6

设从初始状态开始,至发生第一次碰撞以及接下来的从上次碰撞结束至下次碰撞开始的时间间隔依次为t1、t2、t3…t13.由于凹槽A与物块B的碰撞时间不计,故总时间t=t1+t2+t3…+t13.若滑动摩擦力记为f,则f=μmg,交替选择小物块B及凹槽A为研究对象,由动量定理,有

ft1=mu1,

ft2=mv2-mu1,

ft3=mu3-mv2,

…

ft13=mv-mu12,

以上各式两边相加求和,有

f(t1+t2+t3+…+t13)=mv.

代入已知数值,可得从凹槽开始运动到两者相对静止所经历的的时间t=5 s.

仿照上述思路,交替选择小物块B及凹槽A为研究对象,由动能定理,有

…

以上各式两边相加求和,有

代入已知数值,可得凹槽A发生的总位移为12.75m.

对于第(3)问的求解,难度较大,十分繁琐,考生在考场上很难得出正确结果,如果巧妙地运用图像,则可以避繁就简．

由于每碰撞一次凹槽与物块发生一次速度交换,在同一坐标系上两者的速度图线如图7所示,根据碰撞次数可分为13段凹槽,物块的v-t图像在两条连续的匀变速运动图线间转换,故可用匀变速直线运动规律求时间.则

v=v0+at,a=-μg,

解得t=5 s.

凹槽的v-t图像所包围的阴影部分面积即为凹槽的位移大小s2.(等腰三角形面积共分13份,第一份面积为0.5L,其余每份面积均为L)

图7

当然,并不是所有的题目都能用图像法求解,应该具体问题具体分析．实际应用中,如果能巧妙地运用图像法,往往会有意想不到的收获．因此,研究物理学的基本方法(图像法、解析法、模型法、等效法、整体法、隔离法、逆向思维法、假设法等)十分重要,只有在平常的训练中掌握并灵活地选择这些基本方法,才能熟练的加以运用,才能灵活变通地提高运用自己所学的知识和方法去分析、解决实际问题的能力．