对于一道经典传送带问题的再思考
李 鑫
(浙江省桐乡第一中学,浙江 嘉兴 314500)
传送带问题是高中物理经典话题,传送带是力与运动以及能量问题的天然载体,大部分高考题里传送带运动方向都与物块运动方向共线,2014年江苏压轴题中传送带速度与物块速度不共线,不仅于此,此题还考查了驱动传送带电机功率问题,可以说是恢复高考40年来高考物理中关于传送带问题的集大成者.
1 原题展现
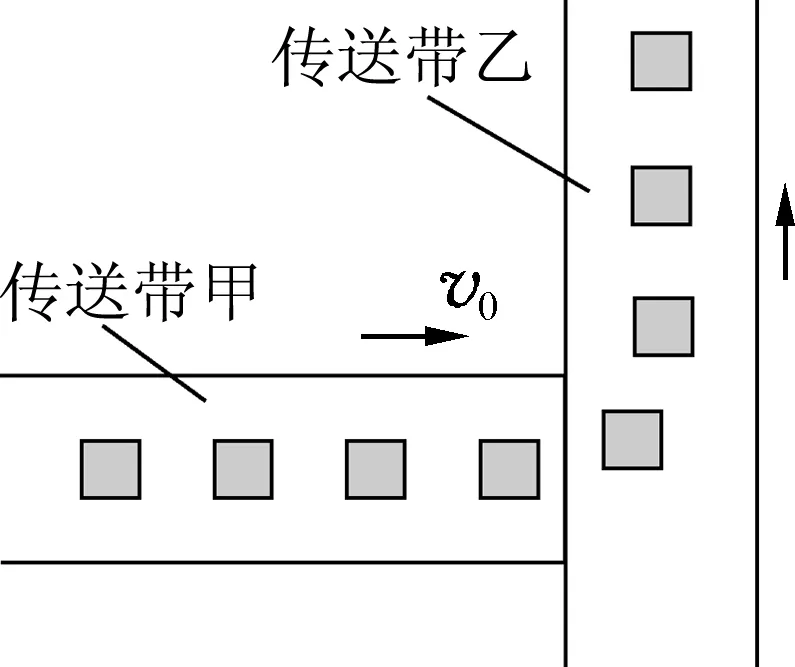
图1
(2014年江苏高考题)如图1所示,生产车间有两个相互垂直且等高的水平传送带甲和乙,甲的速度为v0.小工件离开甲前与甲的速度相同,并平稳地传到乙上,工件与乙之间的动摩擦因数为μ.乙的宽度足够大,重力加速度为g.
(1) 若乙的速度为v0,求工件在乙上侧向(垂直于乙的运动方向)滑过的距离s;
(2) 若乙的速度为2v0,求工件在乙上刚停止侧向滑动时的速度大小v;
(3) 保持乙的速度2v0不变,当工件在乙上刚停止滑动时,下一只工件恰好传到乙上,如此反复.若每个工件的质量均为m,除工件与传送带之间的摩擦外,其他能量损耗均不计,求驱动乙的电动机的平均输出功率.
速度不共线的相对运动不算什么新话题,例如下面例题[1],是早期的一道预赛真题,这类问题的关键是滑动摩擦力的方向与相对运动的方向相反,相对速度方向由矢量加法所决定,滑动摩擦力的大小仍是μN.
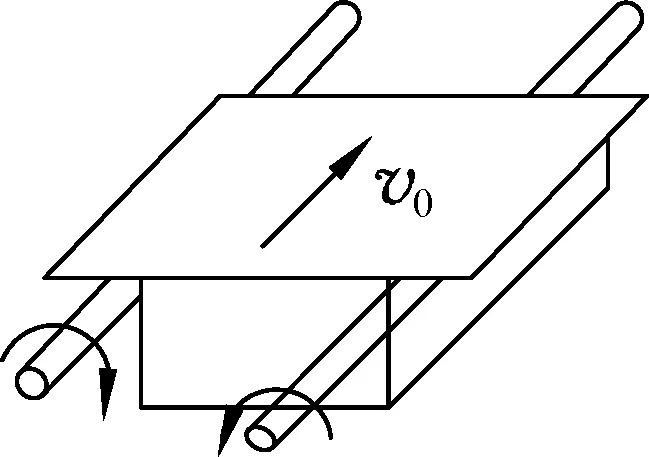
图2
例题.一个质量m=20kg的钢件,架在两根完全相同的、平行的长直圆柱上,如图2所示,钢件的重心与两柱等距,两柱的轴线在同一水平面内,圆柱的半径r=0.025m,钢件与圆柱间的滑动摩擦系数μ=0.20,两圆柱各绕自己的轴线做转向相反的转动,角速度ω=40rad/s,若沿平行于柱轴方向施加力推着钢件做速度为v0=0.05m/s的匀速运动,推力是多大?设钢件左右受光滑槽限制(图中未画出),不发生横向运动.
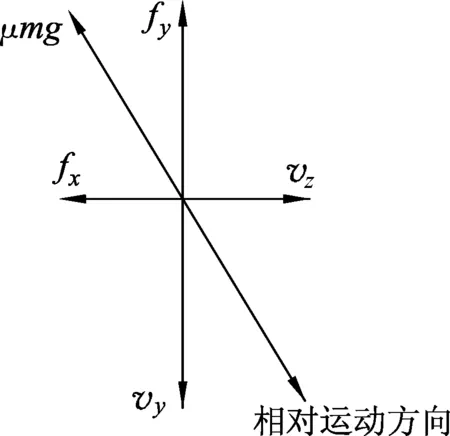
图3
2 相对运动问题讨论
2.1 分析过程
回归到高考问题,如图3所示,当工件进入传送带乙(下文简称乙),工件相对于乙的运动方向沿右下方,所以受到的摩擦力沿左上方.
其实此题前两问是同一个问题的两个侧面,实际上,无论乙的速度如何,工件的速度如何,只要工件停止侧向滑动,在沿乙速度方向一定和乙共速.
以乙为参考系,显然工件相对于乙做匀减速直线运动,摩擦力和初速度方向就是图3标明的方向,所以摩擦力方向不变,意味着摩擦力在x,y方向上分量不变,即两个方向上加速度不变.所以对于第(2)问有
(1)
对于任意初速度比都有
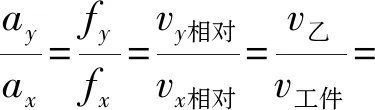
(2)
即x,y方向上加速度比就是工件和乙初速度之比,在两个方向上分别做匀减速直线运动和匀加速直线运动,当匀减速运动结束时候,匀加速运动也刚好结束.
事实上,传送带乙运动的方向甚至不需要和工件速度方向垂直,只要传送带尺度合适,在任意速度夹角下都有这样的结论.
由于两个方向上运动等时性,有
(3)
2.2 相对运动的结论
这个结论分析起来似乎不难,但是有些悖于直觉,觉得过于简单,笔者和诸位前辈讨论的时候,大家一开始都有所怀疑此结论,最大的问题在于摩擦力方向是否不变.考生在考场面对此题,在以前没有仔细研究过此题时,第(2)问是有相当难度的,很容易认为摩擦力方向改变导致无从下手.不过命题者通过第(1)问的铺垫,是有意引导学生往这个结论上“猜”的.
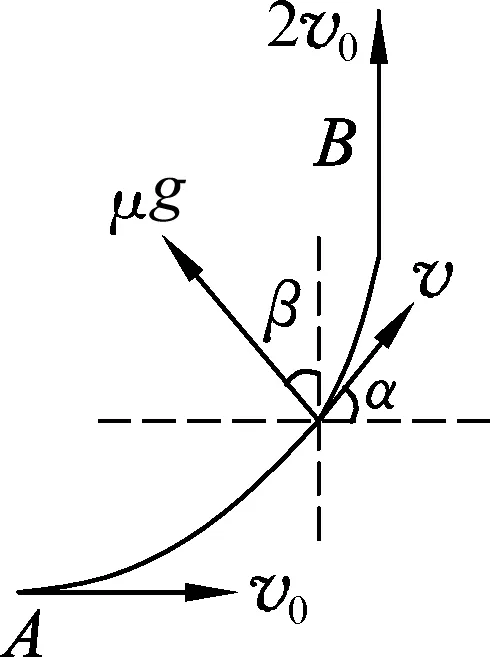
图4
实际上,由于工件相对于乙做匀减速直线运动,所以两个方向上运动可以视作此运动的分运动,显然合运动和分运动具有等时性,而且和速度分量的夹角无关.
2.3 工件相对地面运动
如果以地面为参考系,工件如何运动?由于摩擦力大小方向均不变,工件初速度方向和摩擦力方向不共线,所以物块做的是匀变速曲线运动,也可以说做的是类斜抛运动.轨迹如图4所示,这个结论也很有意思,笔者就这个结论设计了两个问题.
2.3.1 工件结束运动时相对于地面的位移
工件相对于传送带的位移为
(4)
乙相对于地面的位移为
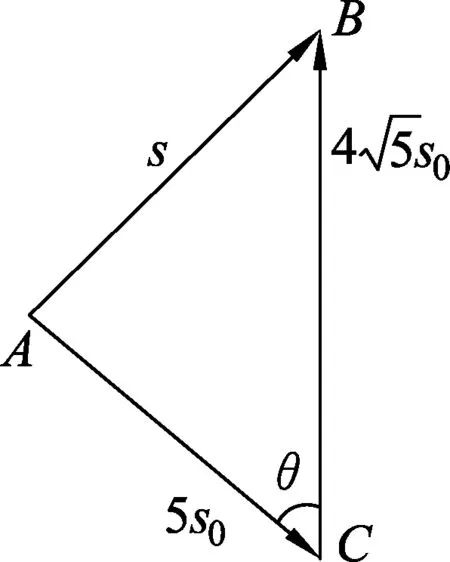
图5
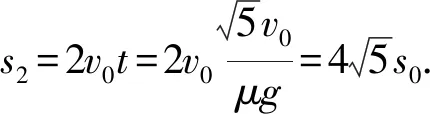
(5)
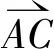
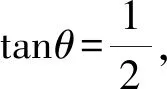
根据余弦定理可知
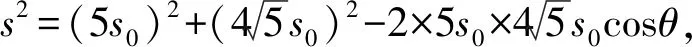
(6)
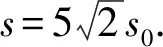
2.3.2 工件在运动过程中速度的最值
开始运动时,工件速度方向与加速度的方向夹角为钝角,共速时是锐角,所以工件先减速后加速,必然有速度最小值.当加速度方向和速度方向垂直时,速度出现最小值.
如图4,显然α=β.所以
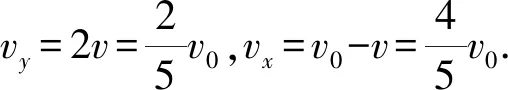
(7)
即最小速度为
对于此问的求解,学生们提供了很多有意思的方案,限于篇幅,不再枚举.通过对试题的挖掘,有益于提升学生追问试题本源的动力,是实践科学探究和培育物理学科素养的良好路径.从表面上看,工件对地轨迹是抛物线和两个方向上直线运动同时结束的结论是相悖的,但本质上却是和谐统一的.
3 驱动电机问题
3.1 分析过程和结论
本题第2个难点是分析传送的驱动电机,关于驱动电机能量的分析学生们很容易陷入思维混乱,遑论本题需要在两个维度上分析清楚.所以本文详细分析速度共线情况,以期挖掘出一些本源的内容.
倘若工件速度和传送带速度方向共线,假设传送带足够长,已知接触面摩擦因数为μ,电动机驱动传送带匀速传动,工件初速度为v,传送带速度是v′.
3.1.1 工件加速
若v (8) s′=v′t. (9) 由于相对运动产生的热量为 Q=μmg(s′-s). (10) 根据能量守恒,电动机在这个过程提供能量为E=Q+Ek=μmgs′. 当v=0,有2s=s′,即Q=Ek. 初速度为0,即对应着本题工件在乙上加速情况.能量关系非常清晰,传送带给工件提供动能,也会有等量热量损耗,所以驱动电机需要给传送带两倍动能. 3.1.2 工件减速 若v>v′,工件减速位移为 根据能量守恒,电动机在这个过程提供能量为E=Q-Ek=-μmgs′. 这个值为负值,工件损耗的动能比产生的热量要多,可以额外供给能量给传送带,无需驱动电机供给能量.因为这里的传送带模型是理想模型,忽略了传送带轮轴能量损耗,也就是说传送带空载情况下不需要提供电能,所以物块减速时动能损耗比产生热量要多,额外的就给了传送带.从力的角度来说,传送带给物块的力是阻力,而物块给传送带是动力,相当于工件给传送带做正功,给传送带补给了能量. 当v′=0,有s′=0,即Q=Ek,就是工件动能全部转化成了热量,电动机无需供给能量.对应的恰好是此题工件侧向滑动的模型. 把传送带上能量关系分开来详细讨论,学生对于驱动电机供能关系一目了然,清晰明确,而且也理解了理想传送带的局限性. 本文首先指出速度不共线的相对运动问题大多为自主招生和预赛难度的试题,对于高考学生,有相当难度.于是文章详细分析此题相对运动模型,发现工件侧向减速到0时,沿传送带乙方向必然同时加速完成,而且与二者速度夹角无关,指出此题前两问展示的是一个更广延结论下的一个特例.然后文章探讨了工件相对于传送带和地面做何运动,分别是匀减速直线运动和类斜抛运动.最后分析了驱动电机问题,给出了工件加速和减速情况下驱动电机能量分配问题,强调理想传送带是忽略转轴间能量损耗,通过分析大大优化了解题过程,使得学生对于此题驱动电机功率问题认知更加清晰深刻.3.2 第(3)问求解
4 结论
——“模型类”相关试题选登

