基于超宽带信号的移动节点的室内定位算法

石 磊，刘 燕

(成都师范学院,四川 成都 611130)

0 引 言

获取设备在环境中的位置是多数位置服务应用的关键。现有的定位算法，如全球定位系统(Global Position System, GPS)，基于视频跟踪或射频-电磁波定位[1-2]。然而，这些定位技术因低定位精度限制了其应用，特别是在室内环境。

目前针对室内环境，学者提出了不同的估计移动设备位置的方案。这些方案使用光信号，如红外、激光、视频跟踪(如Vicon 系统)[3]以及射频信号测距。值得注意的是，室内环境的定位算法应具有低成本、易携带特性。

为此，研究人员提出许多无线射频标准的轻量级定位算法，如WiFi[4-5]、Bluetooth[6]和ZigBee[7-8]。它们都是通过测量两个设备的接收信号强度(Received Signal Strength Indicator, RSSI)测距。然而，这些测距算法的精度低，尤其在非视距环境(Non Line of Sight, NLOS)中。

由于超宽带信号具有高的时间分辨力，能够准确测量信号穿越时间(Time of Flight, TOF)，为定位提供基础。无线传感网络节点 Zyggie[9]就是利用UWB信号测距的、紧凑、轻便的设备。Zyggie采用EFM32 ARM CortexM4微型控制器，控制UWB信号。并且Zyggie利用DecaWave DW100 UWB 无线芯片[10]进行TOF测量。

为此，提出基于UWB的移动节点的室内定位算法BAST。BAST算法通过TOF测量进行测距，然后再依据权重质心定位算法初始估计移动节点位置，并通过三角测量法估计移动节点位置，再通过迭代，选择最优的锚节点组，并修正测距的噪声项。最后，通过最优的锚节点组及噪声修正后的测距估计移动节点位置。仿真结果表明，提出的BAST算法能够有效地估计移动节点位置。

1 定位模型

UWB系统允许发射低功率、超短脉冲，并通过TOF测距，测距过程如下：1)发射器先向接收端发射脉冲信号，当接收端接收信号后就回复信号。而TOF就等于信号往返的时间差，如式(1)所示：

(1)

其中Tem为发射端发射信号时刻。Tre为发射端接收由接收端反馈的信号的时刻。而Tr为接收端对信号的处理时延。

再依据TTOF，推算发射端与接收端间的距离d：

d=TTOF×c

(2)

令θ=[x,y]T，θ∈R3表示移动节点位置。考虑N个锚节点，且它们位置已知。令θi=[xi,yi]T表示这些锚节点位置，且θi∈R3，i=1,2,…,N。

若需估计移动节点位置，至少需要获取与三锚节点间的距离。通过式(2)可获取离三个锚节点间的距离，可建立三个等式：

(3)

其中[xi,yi]T为锚节点的位置，ni为测距噪声，且i=1,2,…,N。

1.1 权重质心定位

引用 文献[11]的权重质心定位(Weighted Centroid Localization, WCL)估计移动节点位置θ：

(4)

其中ai表示第i个锚节点位置矢量，而ωi为锚节点相应的权重。

1.2 三边测量法

先依据式(3)测距，然后再进行等式转换，并结合三边测量法估计移动节点位置θ：

u=V·θ+e

(5)

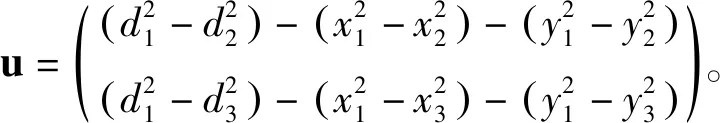
以第一个锚节点作为基准，并引用两个变量：

(6)

依据克拉默法则，通过最小均方误差(Mean Square Error, MSE)，求解移动节点的位置：

(7)

2 BAST定位算法

BAST算法旨在通过选择最优的三个锚节点估计移动节点的位置。移动节点依据式(2)，先计算离锚节点的距离，并形成距离集dA={d1,d2,…,dn}，其中n为移动节点邻居的锚节点数。

然后，先从n个锚节点随机选择一个锚节点作为第一锚节点，然后再依据不共线原则，再从n-1个锚节点中选择两个锚节点，进而构成初始定位锚节点集ψA={A1,A2,A3},其中A1为选择的第一个锚节点，A2、A3分别为选择的第二个、第三个锚节点。所谓定位锚节点集是指用于构成式(3)的方式的三个锚节点。

再依据三边测量法，估计移动节点的位置。为了提高定位精度[12]，构建多个定位锚节点集，并进行迭代，每一组定位锚节点集都利用三边定位算法估计移动节点位置。

假定第i组定位锚节点集ψi所估计的移动节点位置为θi。由于移动节点周围有n个锚节点，可以形成n组定位锚节点集ψi，进而也能有n个移动节点的估计值，如式(8)所示：

fori=1:ndo

ψi←A1by random selected

ψi←A2andA3

θi←Trilateration(A1,A2,A3)

end for

(8)

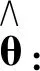
(9)

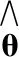
(10)

再计算n个δi的最小值，所对应的θi值，将此θi值表示为θmin。然后依据θmin寻找到产生θi的定位锚节点集ψi={A1,A2,A3}。

回顾到式(3)，测距过程有噪声项n的影响[13]。为此，利用ψi={A1,A2,A3}和θmin，推算噪声项n：

(11)

其中xmin、ymin为θmin的横坐标、纵坐标。

(12)

3 性能仿真

为了更好分析BAST算法的性能，选择如图1所示Zyggie节点，并考虑两个实验。实验一：室内步行；实验二：室内Tennis。

图1 Zyggie 节点结构

3.1 实验一

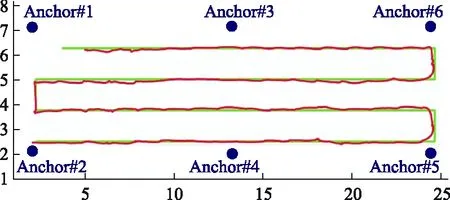
图2 移动节点估计

考虑长为26.4 m和宽为9.2 m的243 m2的房间。移动节点依据图2的绿色线移动，移动速度约3 km/h。为了估计移动节点位置，在房间里部署6个锚节点。

图2的红色线表示BAST算法对移动节点移动轨迹的估计结果。从图2可知，BAST算法能够有效地估计移动节点位置。

表1显示BAST、多点定位法、三边测量和高斯-牛顿和WCL算法的估计精度。选择平均误差(Average Error，AE)、平均标准方差(Average Standard Deviation, ASD)，其表示移动节点所估计的所有点的平均误差。

从表1可知，BAST算法的平均误差最低，WCL算法的平均误差最高，而高斯-牛顿算法的平均误差与BAST算法逼近。这些算法在室内行人慢速移动环境下，定位误差的差异并不大。

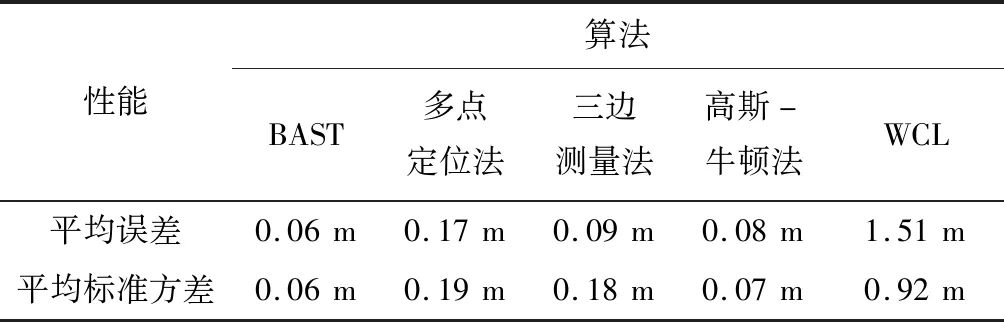
表1 各算法的定位性能比较(实验一)

表2显示了各算法的运算时间。运算时间越长，表明算法越复杂。从表2可知，BAST算法的运算时间最高，达到0.59 ms，远高于其他算法，比多点定位和WCL算法的运行算法时间提高了近2倍。

表2 算法的运算时间(实验一)

3.2 实验二

本次实验分析对网络运动员移动监测、跟踪性能。考虑一个安卓应用系统，运用场景如图3所示。在运动场的角落设置锚节点，图中的蓝色为锚节点位置。将运动员看成节点，通过算法监测节点的移动轨迹。

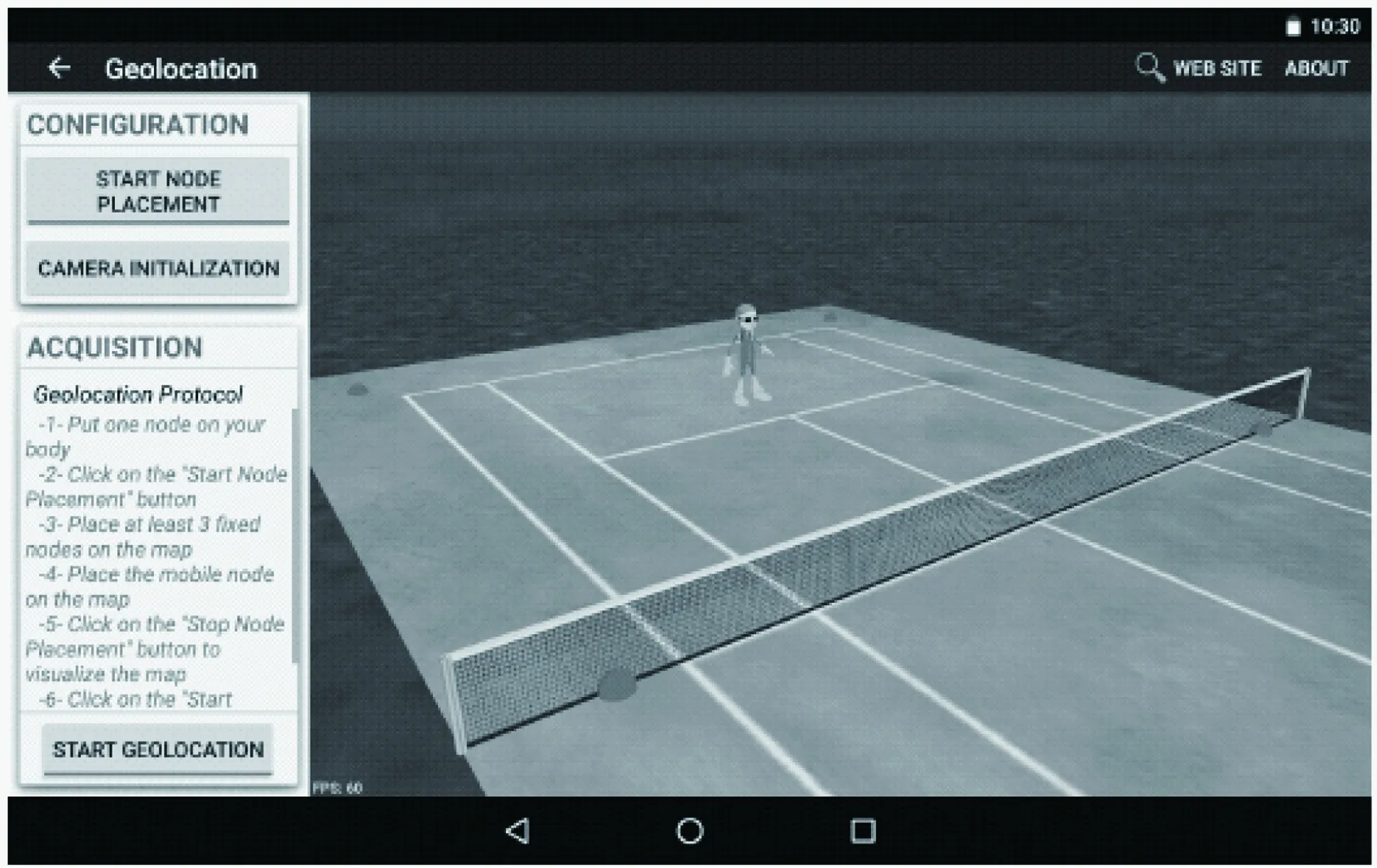
图3 运动场景

表3显示了各算法的移动节点位置跟踪性能。从表3可知，提出的BAST算法的平均误差最低，低至为1.08 m，而WCL算法的平均误差最高，达到4.50 m。而多点定位法、三角测量法和高斯-牛顿法的平均误差分别为1.36 m、2.11 m和1.51m。这也表明，相比其他算法，BAST算法能够有效地跟踪移动节点位置。

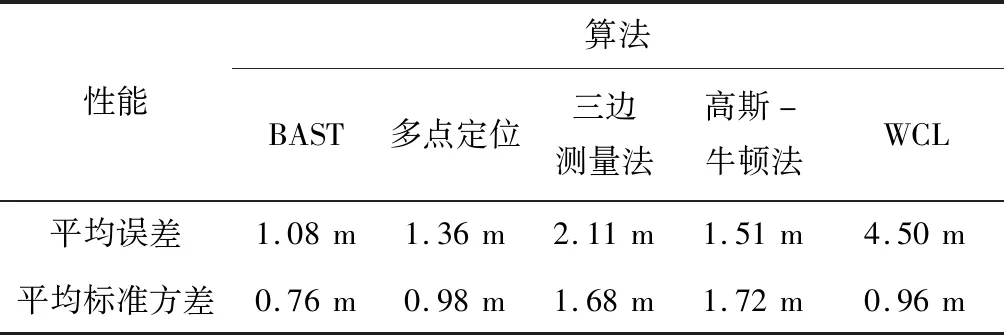
表3 各算法的定位性能比较(实验二)

平均标准方差反映了定位精度的波动。从表3可知，BAST算法的平均标准方差为0.76，远低于三角测量法和高斯-牛顿法的算法。这也表明，BAST算法具有稳定的定位精度。

此外，表4显示了各算法的运算时间。从表4可知，BAST算法的运算时间最高，比三角测量法和WCL算法的运算时间提高了近一倍。结合表3和表4可知，尽管BAST算法提高了定位精度，但运算时间大幅度地提高。但所提高的运算时间量来看，增加的运算时间并不多。例如，BAST算法的运算时间为0.61 ms，而最优的三角测量法的运算时间为0.26 ms，只增加了0.25 ms。

表4 算法的运算时间(实验二)

4 结 语

针对移动节点的室内定位问题，提出了基于UWB信号的移动定位算法BAST。BAST算法通过测量移动节点离锚节点间距离为基础，再结合三边测量法估计移动节点位置。而BAST算法利用UWB无线信号的交互，进行TOF测量，进而估计测距。

引用可穿戴、低功耗、轻量级的Zyggie节点进行实验。考虑步行和网球运动两个场景。通过实验数据表明，BAST算法获取低的定位精度。在步行环境，平均定位误差0.06 m，而网球运动场景，平均定位误差为1.08 m。

通过实验数据可知：高斯-牛顿算法的复杂度低于BAST算法，当移动节点移动缓慢时，高斯-牛顿和BAST算法具有相同性能。但是，在移动速度较快环境，如网球运动场景，BAST算法仍能够获取高的定位精度，远高于其他算法。