热电材料中的晶格热导率

沈家骏, 方腾, 傅铁铮, 忻佳展, 赵新兵, 朱铁军



热电材料中的晶格热导率

沈家骏, 方腾, 傅铁铮, 忻佳展, 赵新兵, 朱铁军

(浙江大学 材料科学与工程学院, 硅材料国家重点实验室, 杭州 310027)

随着可再生能源及能源转换技术的快速发展, 热电材料在发电及制冷领域的应用前景受到越来越广泛的关注。发展具有高热电优值材料的重要性日益突出, 如何获得低晶格热导率是热电材料的研究重点之一。本文阐述了热容、声速及弛豫时间对晶格热导率的影响, 介绍了本征低热导率热电材料所具有的典型特征, 如强非谐性、弱化学键、本征共振散射及复杂晶胞结构等, 并分析了通过多尺度声子散射降低已有热电材料晶格热导率的方法, 其中包括点缺陷散射、位错散射、晶界散射、共振散射、电声散射等多种散射机制。此外, 总结了几种预测材料最小晶格热导率的理论模型, 对快速筛选具有低晶格热导率的热电材料具有一定的理论指导意义。最后, 展望了如何获得低热导率热电材料的有效途径。

热电材料; 晶格热导率; 热容; 弛豫时间; 综述

1 晶格热导率的影响因素

1.1 热容

从晶格热导率的公式可以看出, 晶格热导率与定容热容V成正比, 所以降低V有利于获得低晶格热导率。杜隆-珀蒂定律指出构成固体的各个原子在高温时的热容趋近于极限值3B, 其中B为玻尔兹曼常数, 因此通过改变热容来降低热导率通常比较困难。然而研究人员发现中温Cu2–xSe热电材料的热容随着温度升高会逐渐减小[10-11]。如图1(a)所示, 固体的V为3B,为总原子数。而在液体中, 大部分横向振动波无法传递,V减小到2~2.5B。随着温度升高, Cu2–xSe中Cu离子的高度离域性使材料在一定程度上表现出类液体的行为, 大大降低了横向声学波对热容的贡献, 使得Cu2–xSe在高温条件下的V接近2B。

根据德拜热容模型, 热导的贡献主要来自于声学波。这是由于光学波的波速趋近于0, 对热导率的贡献基本可以忽略[17]。对于多原子体系, 假设每个原胞中的原子数为, 总原胞数为, 则体系总的自由度为3。其中, 声学支有3个, 光学支有3(-1)个[18]。根据能量均分原理可得, 声学支贡献的热容为/, 光学支为(-1)/。因此, 原胞中原子数越多, 声学支对总热容的贡献越小, 越有利于获得低晶格热导率。这在许多具有复杂晶胞结构的热电材料中得到了印证(如图1(b)所示)。例如：Yb14MnSb11与PbTe具有相似的德拜温度, 平均原子质量, 热容及格林内森参数[19-20], 但是由于Yb14MnSb11原胞中原子数为104, 而PbTe只有2, 使得Yb14MnSb11的室温晶格热导率仅有0.6 W·m-1·K-1, 远低于PbTe的2 W·m-1·K-1[21]。

1.2 声速

在热导率公式中,g为声子的群速度, 可以根据声子谱中声学支的斜率得到。在实际研究中, 为了便于测量, 通常假设群速度g与固体声速s相等。研究表明具有弱化学键的化合物通常具有低声速,例如,在-MgAgSb中由于Mg原子本身不存在d轨道, 无法与近邻原子形成强d-d键, 导致Mg原子与Ag原子之间的共价键较弱, 晶格发生一定的扭曲[22]。这种弱键的存在使得-MgAgSb的声速仅有1920 m/s。Ag8GeTe6等体系中也存在同样的现象[23-24], 由于Ag原子与Te原子之间较弱的键合使得Ag8GeTe6声速低至1000~1500 m/s。

图1 (a) Cu2-xSe化合物的热容与温度关系图[11]和(b) 室温晶格热导率与原胞中原子数关系[12-16]

此外, 通过引入重原子的方式也能降低声速,比较典型的例子有笼式化合物及填充方钴矿[25-28]。如图2(a)所示, 在Ba8Ga16Ge30笼式化合物中, Ba原子占据由Ga原子及Ge原子构成的晶格间隙中。若将Ba原子单纯看作散射中心, 则理论预测的声子弛豫时间应为0.18 ps。然而, 中子三轴光谱分析表明加入Ba原子仅仅使纵波弛豫时间L由2.6 ps降为1.3 ps。因此, 低晶格热导率不能只归因于弛豫时间的降低, 声速的降低也起到了重要的作用。如图2(b)和(c)所示, 在笼式结构中, 由于声学声子模与填充原子产生的低频光学支之间存在“避免交叉”现象, 使得声学支的频率进一步降低, 从而具有更低的声速[29]。

1.3 弛豫时间

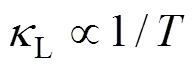
图2 (a)Ba8Ga16Ge30晶体结构示意图, (b)未填充及填充笼式结构的弹簧模型及(c)色散关系[29]

点缺陷散射是一种非常有效的降低材料热导率的方法, 包括质量波动散射与应力场波动散射[54], 二者分别与原子间质量差和半径差有关, 原子间质量差及半径差越大, 点缺陷散射越强。合金化是目前应用最广的增强点缺陷散射的手段, 在Bi2Te3[55-56]、Pb(Te,Se)[57]、CuInTe2[58]、Mg2(Si,Sn)[59-60]、SiGe合金[61]以及Half-Heusler(HH)合金[62-69]中都有应用。以FeNbSb基HH合金为例, 研究表明Nb位Ta合金化可以有效降低FeNbSb的晶格热导率[70]。如图4(a)及(b)所示, 虽然Nb和Ta之间较小的原子半径差使应力场波动散射较弱, 但两者较大的原子质量差可以引入强烈的质量波动散射, 使其最小晶格热导率降至1.3 W·m–1·K–1。除了合金化之外, 空位与间隙原子也属于一种较为特殊的点缺陷散射机制。19电子HH合金Nb0.8CoSb中存在近20%的本征Nb空位,使Nb0.8CoSb合金具有相对较低的晶格热导率[71]。Cu2SnSe4等热电材料中也存在同样的现象[72]。

晶界散射及位错散射也是非常重要的降低晶格热导率的方法[73]。常用的增强晶界散射的手段有球磨[74-75]和甩带[76-79]两种方法, 广泛应用于Bi2Te3[79]、SiGe[80]以及Half-Heusler合金[81]等热电材料中。对于位错散射, 有报道称在Bi0.5Sb0.15Te3中通过过量Te液相烧结的手段可以增加晶界位错阵列[8]。另外, 通过向材料中添加第二相的方式也能增加位错密度[82], 这一现象在PbTe-PbS体系中得到了印证[83]。

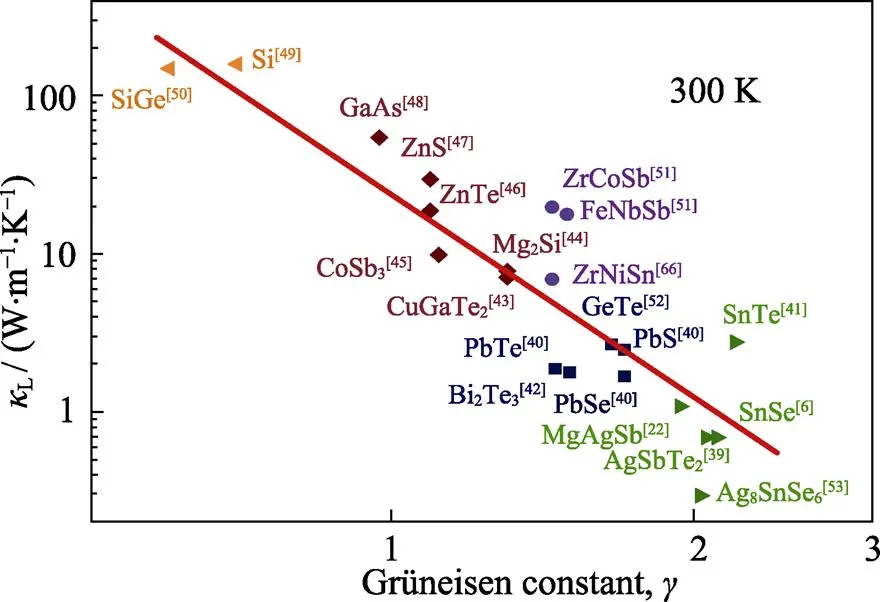
图3 格林内森常数与室温晶格热导率的关系图[6, 22, 39-53]

图4 (a)(Nb0.6Ta0.4)0.8Ti0.2FeSb和Nb0.8Ti0.2FeSb的晶格热导率与声子频率的依赖关系和(b)Ta掺杂量与无序散射因子及晶格热导率的关系图[70]

此外, 位错还可以通过自身空位的聚集产生。如图5所示, 在Mg2Si1–xSb材料[84]中, Sb的高剂量合金化产生大量Mg空位, 使得空位浓度远高于平衡空位密度, 多余的Mg空位自发地发生聚集从而形成位错。在Mg2Si0.5Sb0.5中, 位错密度高达2.8×1016m−2。图5(b)为Sn及Sb元素合金化对Mg2Si晶格热导率的不同影响。由于Sn元素的加入不会增加Mg空位的浓度从而产生位错, 晶格热导率的降低主要来自点缺陷散射的作用。而Sb合金化不仅能增强点缺陷散射, 而且能增强位错散射, 因此具有更低的晶格热导率。此外, 在NaEu0.03Pb0.97–yTe体系[7]中也观察到类似的现象。研究表明随着Na掺杂量的增加, 体系中的主要微观缺陷由点缺陷逐步过渡到位错及纳米颗粒。位错散射使PbTe的晶格热导率下降到0.4 W·m-1·K-1以下。

图5 (a) Mg2Si0.5Sb0.5中位错的IFFT图及相应的应力扫描图, (b) Mg2Si1-xSbx及Mg2Si1–zSnz的室温晶格热导率对比图[84]

除此之外, 共振散射一般出现在具有特殊晶体结构的热电材料中, 如笼式化合物及方钴矿等[29, 85-86]。通过加入填充原子, 可以引入特定频率的共振谱, 从而降低材料热导率。在S0.5Co4Sb10.5Te1.5中S作为填充原子, 可以在声子谱中引入一段频率较低的光学支, 与声学支发生光声耦合现象, 增强共振散射, 最终使得CoSb3材料获得极低的晶格热导率[87]。另外, 最近的研究表明一些具有拓扑绝缘性的热电材料中也存在共振散射。如图6所示, 在BiSe材料中额外的Bi2原子层同样可以引起局域共振效应, 强烈的光声耦合显著降低了BiSe的晶格热导率, 使其室温晶格热导率仅为0.6 W×m-1×K-1[88]。

相比于其他类型的散射机制, 电声散射的研究相对较少。然而, 对于具有较大载流子有效质量的体系, 通常需要较高的载流子浓度使其电性能达到最佳[89-92]。因此, 在这些体系中需要考虑电声散射对晶格热导率的影响。如图7所示, 在多晶硅中掺入P使其晶格热导率显著降低, 0.1at%的P掺杂量就可以使多晶硅室温时的晶格热导率降低60%。但由于P与Si在元素周期表中的位置接近, 具有相似的质量和半径, 因此点缺陷散射不足以解释其晶格热导率的大幅度降低, 必然存在其他散射机制的作用。研究表明P元素的掺杂作用可以引起多晶硅中载流子浓度的增加, 使电声相互作用显著增强。当掺入6at%的P时, 电声散射对晶格热导率的降低作用占所有散射机制的36%, 接近晶界散射的作用[93]。

图6 BiSe晶体结构示意图(a)和Bi2Se3及BiSe的晶格热导率对比图(b)[88]

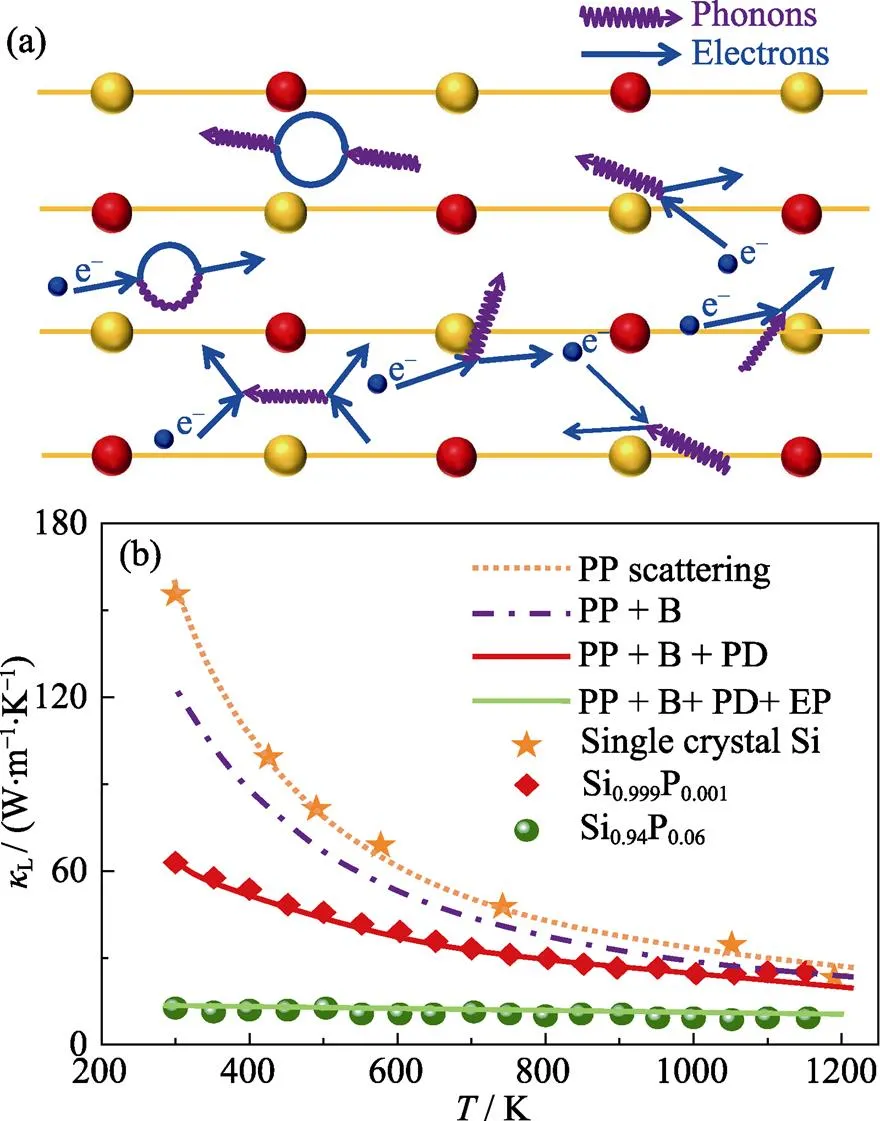
图7 电声散射示意图(a)和硅样品晶格热导率的实验值与Callaway模型计算值的对比图(b)[93]

2 最小晶格热导率

图8 (a)扩散子模型及声子模型的差别示意图和(b)Cahill模型及扩散子模型预测的最小晶格热导率对比图

虽然最小晶格热导率的计算模型有所不同, 但不同模型预测出的结果大都比较接近。这主要由两方面原因造成的：首先, 大多数材料达到最小晶格热导率时, 温度均远远高于德拜温度, 此时, 热容已经趋近于极限值3; 其次, 所有模型都假设对热导率的贡献全部由平均自由程等于原子间距尺度的声子贡献, 这一假设使得晶体中尺度大于原子间距的缺陷, 如位错、第二相等不会对最小晶格热导率的预测产生影响。

图9 获得低晶格热导率的几种途径

3 结束语

晶格热导率是一个可以相对独立调控的影响材料热电性能的参数。本文分别阐述了热容、声速及弛豫时间等三个物理量对晶格热导率的影响, 并介绍了几种不同类型的预测材料最小晶格热导率的理论模型, 对降低材料的晶格热导率具有重要的指导意义。那么如何从实验上获得较低的晶格热导率呢? 主要可以从以下两方面考虑：

第一、寻找并制备具有本征低热导率的热电材料。具有本征低热导率的热电材料一般具有以下几个特征：1. 强非谐性。非谐性强弱主要与化学键及原子平衡位置的对称性有关。原子在振动过程中, 若其对称中心发生偏移越大, 则非对称性越强。具有孤对电子的材料往往由于电子云分布不均匀, 晶体结构会发生一定的变形, 非对称性显著增强, 有利于获得强非谐性; 2. 弱化学键。化学键弱的材料具有较低的声速, 原子在其平衡位置附近具有更大的活动空间, 电子云分布更为弥散。在声子谱中, 弱化学键往往对应一些低频段的声子模, 更容易与声学支发生耦合作用, 从而进一步降低声学支对热导的贡献; 3. 复杂的晶胞结构。一方面可以降低声学支对总热容的贡献比重, 另一方面可以降低声学支声子的群速。

第二、通过多尺度声子散射降低已有热电材料的热导率。由于在德拜温度以上, 声子频率分布在0到德拜频率之间, 同时抑制所有波长段的声子模能够有效降低晶格热导率, 如点缺陷散射、位错散射、晶界散射、共振散射和电声散射等(如图9所示)。

近年来有研究表明, 弱拓扑绝缘体能实现极低的晶格热导率[101-103], 并且其特殊的表面传导特性有望冲破半导体基热电材料的禁锢, 实现电性能及热性能的真正解耦。然而, 拓扑绝缘体的晶格动力学、声子输运等机制仍需要人们进一步研究与探索[104-105]。总的来说, 不论是研究发现新型的具有本征低晶格热导率的热电材料, 还是对现有的热电材料热导率进一步的降低, 通过多种手段的并用, 一定会对未来的热电材料领域的可持续发展产生实质的积极促进作用。

[1] BELL L E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems., 2008, 321(5895): 1457–1461.

[2] SNYDER G J, TOBERER E S. Complex thermoelectric materials., 2008, 7:101–110.

[3] XIN J Z, TANG Y L, LIU Y T,Valleytronics in thermoelectric materials., 2018, 3(1): 9.

[4] LI W, ZHENG L L, GE B H,Promoting SnTe as an eco-friendly solution for p-PbTe thermoelectricband convergence and interstitial defects., 2017, 29(17): 1605887-1-8.

[5] BISWAS K, HE J Q, BLUM I D,High-performance bulk thermoelectrics with all-scale hierarchical architectures., 2012, 489: 414–418.

[6] ZHAO L D, LO S H, ZHANG Y S,Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals., 2014, 508: 373–377.

[7] CHEN Z W, JIAN Z Z, LI W,Lattice dislocations enhancing thermoelectric PbTe in addition to band convergence., 2017, 29(23): 1606768-1-8.

[8] KIM S I, LEE K H, MUN H A,Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics., 2015, 348(6230): 109–114.

[9] CHEN Z W, ZHANG X Y, PEI Y Z. Manipulation of phonon transport in thermoelectrics., 2018, 30(17): 1705617-1-12.

[10] HE Y, DAY T, ZHANG T S,High thermoelectric performance in non-toxic earth-abundant copper sulfide., 2014, 26(23): 3974–3978.

[11] LIU H L, SHI X, XU F FCopper ion liquid-like thermoelectrics., 2012, 11: 422–425.

[12] VINING C B, LASKOW W, HANSON J O,Thermoelectric properties of pressure-sintered Si0.8Ge0.2thermoelectric alloys., 1991, 69(8): 4333–4340.

[13] PEI Y Z, LALONDE A, IWANAGA S,High thermoelectric figure of merit in heavy hole dominated PbTe., 2011, 4(6): 2085–2089.

[14] ZEVALKINK A, TOBERER E S, ZEIER W G.,Ca3AlSb3: an inexpensive, non-toxic thermoelectric material for waste heat recovery., 2011, 4(2): 510–518.

[15] MAY A F, TOBERER E S, SARAMAT A,Characterization and analysis of thermoelectric transport in n-type Ba8Ga16−xGe30+x., 2009, 80(12): 125205-1-12.

[16] COX C A, TOBERER E S, LEVCHENKO A A,Structure, heat capacity, and high-temperature thermal properties of Yb14Mn1−xAlSb11., 2009, 21(7): 1354–1360.

[17] SLACK G A. The thermal conductivity of nonmetallic crystals., 1979, 34: 1–71.

[18] TOBERER E S, ZEVALKINK A, SNYDER G J. Phonon engineering through crystal chemistry., 2011, 21(40): 15843–15852.

[19] WANG Y, HU Y J, FIRDOSY S A,First-principles calculations of lattice dynamics and thermodynamic properties for Yb14MnSb11., 2018, 123(4): 045102-1-10.

[20] BROWN S R, KAUZLARICH S M, GASCOIN F,Yb14MnSb11:  new high efficiency thermoelectric material for power generation., 2006, 18(7): 1873–1877.

[21] CHEN Z, LI D C, DENG S P,Thermoelectric properties and thermal stability of Bi-doped PbTe single crystal., 2018, 538: 154–159.

[22] YING P J, LI X, WANG Y C,Hierarchical chemical bonds contributing to the intrinsically low thermal conductivity in-MgAgSb thermoelectric materials., 2016, 27(1): 1604145-1-8.

[23] LI J Q, LI L F, SONG S H,High thermoelectric performance of GeTe–Ag8GeTe6eutectic composites., 2013, 565: 144–147.

[24] FUJIKANE M, KUROSAKI K, MUTA H,Thermoelectric properties of Ag8GeTe6., 2005, 396(1): 280–282.

[25] HOU Y H, CHANG L S. Optimization on the figure-of-merit of p-type Ba8Ga16Ge30type-I clathrate grownthe Bridgman method by fine tuning Ga/Ge ratio., 2018, 736: 108–114.

[26] YAN X L, IKEDA M, ZHANG L,Suppression of vacancies boosts thermoelectric performance in type-I clathrates., 2018, 6(4): 1727–1735.

[27] BEEKMAN M, VANDERGRAAFF A. High-temperature thermal conductivity of thermoelectric clathrates., 2017, 121(20): 205105.

[28] GONZALEZ-ROMERO R L, ANTONELLI A. Estimating carrier relaxation times in the Ba8Ga16Ge30clathrate in the extrinsic regime., 2017, 19(4): 3010–3018.

[29] CHRISTENSEN M, ABRAHAMSEN A B, CHRISTENSEN N B,Avoided crossing of rattler modes in thermoelectric materials., 2008, 7: 811–815.

[30] CALLAWAY J. Model for lattice thermal conductivity at low temperatures., 1959, 113(4): 1046–1051.

[31] CHUNG J D, MCGAUGHEY A J H, KAVIANY M. Role of phonon dispersion in lattice thermal conductivity modeling., 2004, 126(3): 376–380.

[32] SLACK G A, GALGINAITIS S. Thermal conductivity and phonon scattering by magnetic impurities in CdTe., 1964, 133(1A): A253–A268.

[33] HEREMANS J P. Thermoelectric materials: the anharmonicity blacksmith., 2015, 11: 990–991.

[34] QIU W J, XI L L, WEI P,Part-crystalline part-liquid state and rattling-like thermal damping in materials with chemical-bond hierarchy., 2014, 111(42): 15031–15035.

[35] TYAGI K, GAHTORI B, BATHULA S,Thermoelectric properties of Cu3SbSe3with intrinsically ultralow lattice thermal conductivity., 2014, 2(38): 15829–15835.

[36] DELAIRE O, MA J, MARTY K,Giant anharmonic phonon scattering in PbTe., 2011, 10: 614–619.

[37] LEE S, ESFARJANI K, LUO T F,Resonant bonding leads to low lattice thermal conductivity., 2014, 5: 3525-1-8.

[38] MURPHY R M, MURRAY ÉD, FAHY S,Ferroelectric phase transition and the lattice thermal conductivity of Pb1−xGeTe alloys., 2017, 95(14): 144302-1-8.

[39] CHEN Y, HE B, ZHU T J,Thermoelectric properties of non-stoichiometric AgSbTe2based alloys with a small amount of GeTe addition., 2012, 45(11): 115302.

[40] ZHANG Y, KE X Z, CHEN C F,Thermodynamic properties of PbTe, PbSe, and PbS: first-principles study., 2009, 80(2): 024304-1-12.

[41] MILLER A J, SAUNDERS G A, YOGURTCU Y K. Pressure dependences of the elastic constants of PbTe, SnTe and Ge0.08Sn0.92Te., 1981, 14(11): 1569–1584.

[42] ALEXANDER F Z, VOLKER L D, RALF P S,lattice dynamics and thermochemistry of layered bismuth telluride (Bi2Te3)., 2016, 28(11): 115401-1-7.

[43] RINCÓN C, VALERI-GIL M L, WASIM S M. Room-temperature thermal conductivity and grüneisen parameter of the I-III-VI2chalcopyrite compounds., 1995, 147(2): 409–415.

[44] WANG H F, JIN H, CHU W G,Thermodynamic properties of Mg2Si and Mg2Ge investigated by first principles method., 2010, 499(1): 68–74.

[45] BERNSTEIN N, FELDMAN J L, SINGH D J. Calculations of dynamical properties of skutterudites: thermal conductivity, thermal expansivity, and atomic mean-square displacement., 2010, 81(13): 134301-1-11.

[46] BHASKAR A, PAI Y H, WU W M,Low thermal conductivity and enhanced thermoelectric performance of nanostructured Al-doped ZnTe., 2016, 42(1, Part B): 1070–1076.

[47] KATRE A, TOGO A, TANAKA I,First principles study of thermal conductivity cross-over in nanostructured zinc-chalcogenides., 2015, 117(4): 045102-1-6.

[48] NUNES O A C. Piezoelectric surface acoustical phonon amplification in graphene on a GaAs substrate., 2014, 115(23): 233715-1-7.

[49] REEBER R R. Thermal expansion of some group IV elements and ZnS., 1975, 32(1): 321–331.

[50] QIN L, TEO K L, SHEN Z X,Raman scattering of Ge/Si dot superlattices under hydrostatic pressure., 2001, 64(7): 075312-1-5.

[51] SILPAWILAWAN W, KUROSAKI K, OHISHI Y,FeNbSb p-type half-Heusler compound: beneficial thermomechanical properties and high-temperature stability for thermoelectrics., 2017, 5(27): 6677–6681.

[52] BOSONI E, SOSSO G C, BERNASCONI M. Grüneisen parameters and thermal conductivity in the phase change compound GeTe.,2017, 16 (4): 997–1002.

[53] LI W, LIN S, GE B,Low sound velocity contributing to the high thermoelectric performance of Ag8SnSe6., 2016, 3 (11): 1600196-1-7.

[54] CALLAWAY J, VON B, HANS C. Effect of point imperfections on lattice thermal conductivity., 1960, 120(4): 1149–1154.

[55] HAO F, QIU P F, TANG Y S,High efficiency Bi2Te3-based materials and devices for thermoelectric power generation between 100 and 300 ℃., 2016, 9(10): 3120–3127.

[56] HU L P, ZHU T J, LIU X H,Point defect engineering of high-performance bismuth-telluride-based thermoelectric materials., 2014, 24(33): 5211–5218.

[57] PEI Y Z, SHI X Y, LALONDA A,Convergence of electronic bands for high performance bulk thermoelectrics., 2011, 473(7345): 66–69.

[58] QIN Y T, QIU P F, SHI X,. Thermoelectric properties for CuInTe2–xS(= 0, 0.05, 0.1, 0.15) solid solution., 2017, 32(11): 1171–1176.

[59] JIANG G Y, HE J, ZHU T J,High performance Mg2(Si,Sn) solid solutions: a point defect chemistry approach to enhancing thermoelectric properties., 2014, 24(24): 3776–3781.

[60] LIU X H, ZHU T J, WANG H,Low electron scattering potentials in high performance Mg2Si0.45Sn0.55based thermoelectric solid solutions with band convergence., 2013, 3(9): 1238–1244.

[61] TRIPATHI M N, BHANDARI C M. High-temperature thermoelectric performance of Si-Ge alloys., 2003, 15(31): 5359–5370.

[62] FU C G, ZHU T J, PEI Y Z,High band degeneracy contributes to high thermoelectric performance in p-type half-Heusler compounds., 2014, 4(18): 1400600-1-6.

[63] YU J J, XIA K Y, ZHAO X B,High performance p-type half-Heusler thermoelectric materials., 2018, 51(11): 113001.

[64] SHEN J J, FU C G, LIU Y T,Enhancing thermoelectric performance of FeNbSb half-Heusler compound by Hf-Ti dual-doping., 2018, 10: 69–74.

[65] ZHU T J, LIU Y T, FU C G,Compromise and synergy in high-efficiency thermoelectric materials., 2017, 29(14): 1605884-1-26.

[66] FU C G, WU H J, LIU Y T,Enhancing the figure of merit of heavy-band thermoelectric materials through hierarchical phonon scattering., 2016, 3(8): 1600035-1-6.

[67] ZHU T J, FU C G, XIE H H,High efficiency half-Heusler thermoelectric materials for energy harvesting., 2015, 5(19): 1500588-1-7.

[68] FU C G, BAI S Q, LIU Y T,Realizing high figure of merit in heavy-band p-type half-Heusler thermoelectric materials.., 2015, 6: 8144.

[69] XIE H H, WANG H, PEI Y Z,Beneficial contribution of alloy disorder to electron and phonon transport in half-heusler thermoelectric materials., 2013, 23(41): 5123–5130.

[70] YU J J, FU C G, LIU Y T,Unique role of refractory ta alloying in enhancing the figure of merit of NbFeSb thermoelectric materials., 2018, 8(1): 1701313-1-8.

[71] XIA K Y, LIU Y T, ANAND S,Enhanced thermoelectric performance in 18-electron Nb0.8CoSb half-heusler compound with intrinsic Nb vacancies., 2018, 28(9): 1705845-1-7.

[72] LI W, LIN S Q, ZHANG X Y,Thermoelectric properties of Cu2SnSe4with intrinsic vacancy., 2016, 28(17): 6227–6232.

[73] KLEMENS P G. The scattering of low-frequency lattice waves by static imperfections., 1955, 68(12): 1113–1128.

[74] ZHANG S N, HE J, JI X H,Effects of ball-milling atmosphere on the thermoelectric properties of TAGS-85 compounds., 2009, 38(7): 1142–1147.

[75] LI Y, MEI D Q, WANG H,Reduced lattice thermal conductivity in nanograined Na-doped PbTe alloys by ball milling and semisolid powder processing., 2015, 140: 103–106.

[76] HONG M, CHEN Z G, ZOU J. Fundamental and progress of Bi2Te3-based thermoelectric materials., 2018, 27(4): 048403-1-46.

[77] XIE J, OHISHI Y, ICHIKAWA S,Naturally decorated dislocations capable of enhancing multiple-phonon scattering in Si-based thermoelectric composites., 2018, 123(11): 115114-1-8.

[78] YU Y, HE D S, ZHANG S Y,Simultaneous optimization of electrical and thermal transport properties of Bi0.5Sb1.5Te3thermoelectric alloy by twin boundary engineering., 2017, 37: 203–213.

[79] XIE W J, HE J, KANG H J,Identifying the specific nanostructures responsible for the high thermoelectric performance of (Bi,Sb)2Te3nanocomposites., 2010, 10(9): 3283–3289.

[80] YANG X Y, WU J H, REN D D,Microstructure and thermoelectric properties of p-type Si80Ge20B0.6-SiC nanocomposite., 2016, 31(9): 997–1003.

[81] YU C, XIE H H, FU C G,High performance half-Heusler thermoelectric materials with refined grains and nanoscale precipitates., 2012, 27(19): 2457–2465.

[82] HU L P, WU H J, ZHU T J,Tuning multiscale microstructures to enhance thermoelectric performance of n-type bismuth-telluride-based solid solutions., 2015, 5(17): 1500411-1-13.

[83] HE J Q, GIRARD S N, KANATZIDIS M G,Microstructure-lattice thermal conductivity correlation in nanostructured PbTe0.7S0.3thermoelectric materials., 2010, 20(5): 764–772.

[84] XIN J Z, WU H J, LIU X H,Mg vacancy and dislocation strains as strong phonon scatterers in Mg2Si1−xSbthermoelectric materials., 2017, 34: 428–436.

[85] SHI X, BAI S Q, XI L L,Realization of high thermoelectric performance in n-type partially filled skutterudites., 2011, 26(15): 1745–1754.

[86] KEPPENS V, MANDRUS D, SALES B C,Localized vibrational modes in metallic solids., 1998, 395: 876–878.

[87] DUAN B, YANG J, SALVADOR J R,Electronegative guests in CoSb3., 2016, 9(6): 2090–2098.

[88] SAMANTA M, PAL K, PAL P,Localized vibrations of bi bilayer leading to ultralow lattice thermal conductivity and high thermoelectric performance in weak topological insulator n-type BiSe., 2018, 140(17): 5866–5872.

[89] UHER C, YANG J, HU S,Transport properties of pure and doped MNiSn (M=Zr, Hf)., 1999, 59(13): 8615–8621.

[90] LI J F, LIU W S, ZHAO L D,High-performance nanostructured thermoelectric materials., 2010, 2(4): 152–158.

[91] FANG T, ZHAO X B, ZHU T J. Band Structures and transport properties of high-performance half-heusler thermoelectric materials by first principles., 2018, 11(5): 847.

[92] TANG Y L, LI X S, MARTIN L H J,Impact of Ni content on the thermoelectric properties of half-Heusler TiNiSn., 2018, 11(2): 311–320.

[93] ZHU T J, YU G T, XU J,The role of electron-phonon interaction in heavily doped fine-grained bulk silicons as thermoelectric materials., 2016, 2(8): 1600171.

[94] ABELES B. Lattice thermal conductivity of disordered semiconductor alloys at high temperatures., 1963, 131(5): 1906–1911.

[95] CLARKE D R. Materials selection guidelines for low thermal conductivity thermal barrier coatings., 2003, 163: 67–74.

[96] CAHILL D G, POHL R O. Heat flow and lattice vibrations in glasses., 1989, 70(10): 927–930.

[97] CAHILL D G, WATSON S K, POHL R O. Lower limit to the thermal conductivity of disordered crystals.1992, 46(10): 6131–6140.

[98] ALLEN P B, DU X Q, MIHALY L,Thermal conductiity of insulating Bi2Sr2YCu2O8and superconducting Bi2Sr2CaCu2O8: failure of the phonon-gas picture., 1994, 49(13): 9073–9079.

[99] FELDMAN J L, ALLEN P B, BICKHAM S R. Numerical study of low-frequency vibrations in amorphous silicon., 1999, 59(5): 3551–3559.

[100] AGNE M T, HANUS R, SNYDER G J. Minimum thermal conductivity in the context of diffuson-mediated thermal transport., 2018, 11(3): 609–616.

[101] POHL R O. Lattice vibrations of glasses., 2006, 352(32): 3363–3367.

[102] FU C G, ZHU T J, LIU Y T,Band engineering of high performance p-type FeNbSb based half-Heusler thermoelectric materials for figure of merit>1., 2015, 8(1): 216–220.

[103] WEI P, YANG J, GUO L,Minimum thermal conductivity in weak topological insulators with bismuth-based stack structure., 2016, 26(29): 5360–5367.

[104] RASCHE B, ISAEVA A, RUCK M,Stacked topological insulator built from bismuth-based graphene sheet analogues., 2013, 12(5): 422–425.

[105] PAULY C, RASCHE B, KOEPERNIK K,Subnanometre-wide electron channels protected by topology., 2015, 11(4): 338–343.

Lattice Thermal Conductivity in Thermoelectric Materials

SHEN Jia-Jun, FANG Teng, FU Tie-Zheng, XIN Jia-Zhan, ZHAO Xin-Bing, ZHU Tie-Jun

(State Key Laboratory of Silicon Materials, School of Materials Science and Engineering, Zhejiang University, Hangzhou 310027, China)

With rapid development of sustainable energies and energy conversion technologies, application prospect of thermoelectric (TE) materials in power generation and cooling has received increasing attention. The requirement of improving TE materials with high figure of merit becomes much more important. How to obtain the low lattice thermal conductivity is one of the main concerns in TE materials. In this review, the influences of specific heat, phonon group velocity and relaxation time on the lattice thermal conductivity are discussed, respectively. Several typical features of TE materials with intrinsic low lattice thermal conductivity are introduced, such as strong anharmonicity, weak chemical bonds and complex primitive cells. Introducing multiscale phonon scatterings to reduce the lattice thermal conductivity of known TE materials is also presented and discussed, including but not limited to point defect scattering, dislocation scattering, boundary scattering, resonance scattering and electron-phonon scattering. In addition, some theoretical models of the minimum lattice thermal conductivity are analyzed, which has certain theoretical significance for rapid screening of TE materials with low lattice thermal conductivity. Finally, the efficient ways to obtain the low lattice thermal conductivity for TE property optimization are proposed.

thermoelectric materials; lattice thermal conductivity; specific heat; relaxation time; review

TB34

A

1000-324X(2019)03-0260-09

10.15541/jim20180320

2018-07-16;

2018-09-03

国家自然科学基金(51725102, 51761135127, 11574267) National Natural Science Foundation of China (51725102, 51761135127, 11574267)

沈家骏(1992-), 男, 博士研究生. E-mail: 11626058@zju.edu.cn

朱铁军, 教授. E-mail: zhutj@zju.edu.cn