一种应用于无线软件定义网络的流表数量约减方法

孔剑锋 刘振海

1(盐城工学院教务处 江苏 盐城 224051)2(盐城工学院信息工程学院 江苏 盐城 224051)

0 引 言

近年来，无线SDN(W-SDN)技术被广泛应用于传感器网络[1-2]、5G通信网络、M2M通信等应用场景中，用来实现可控路由、灵活流量工程和集中式网络管理等功能。然而，由于SDN技术最初的设计目标为有线局域网场景，因此在将SDN技术应用于无线网络环境之前，仍然存在一些问题需要解决。其中，如何有效地减少W-SDN中所需的流表数量从而提高网络的性能和效率，是当前最迫切需要解决的问题之一。

由于W-SDN继承了SDN的框架以及基于流表的转发模式，因此为了实现W-SDN中对于流量路由的可控性，W-SDN的中央控制器必须为每流在路由的每一跳上安装流表。因此，每个无线节点必须以流表的形式存储较多的状态信息，从而导致三个问题：首先，通常情况下，无线节点的存储空间比有线网络中的网络设备小得多，从而只能安装少量流表在每个节点中。因此，网络可容纳的最大流量数量相当有限。其次，当流表数量较多时，流表匹配过程可能消耗过多的能量，从而缩短无线节点的使用寿命。第三，无线节点的处理能力通常较弱，以至于太多的流表可能会带来较大的查表延迟。

一般情况下，解决W-SDN流表数量的方法有两种。第一种方式是流量工程[3-5]，通过这种方式流量可以更加均匀地分布，因此每个节点中的流表数量也获得了平均，从而能够避免某个节点存储过多的流表。第二种方式是源路由，它将路由信息存储在分组报头中，而不是无线节点的流表中[6-7]。因此，使用源路由，无线节点不需要存储流量状态信息，但是需要数据包带有更长的包头，从而导致带宽浪费和可扩展性的降低。针对以上两种方法的不足，在本文中，我们提出了一种称为LSP(Label Switch Path)重用的新型机制，相比于以上两种方法，它可以通过更短的数据包头部，实现最好的流表约减效果。为了实现这种方法，我们将MPLS中的标签交换路径LSP(Label Switch Path)引入到W-SDN中。基于Openflow支持的标签弹出(Pop)，压入(Push)和交换(Swap)操作，我们在数据包头中嵌入多个标签，并使用生存时间TTL(Time To Live)控制数据包在某个LSP上传输的跳数，从而使得数据包能够在不同的LSP之间切换。因此，同一条LSP可以具有不同源和目的地的流量重用，单个流量可以使用不同的LSP完成端到端的传输。在这种机制下，安装在每个无线节点中的流表仅与通过节点的LSP相关，而与流量的数量无关。因此，可以有效减少每个节点维护的状态信息。

综上所述，本文的贡献主要如下：

(1) 提出了一种LSP重用方法来解决无线SDN中的流表数量约减问题；给出了该方法的详细设计和实现，并在软件平台上实现了原型系统。

(2) 研究了最优的LSP规划问题；建立了最小化流表数量的数学模型；提出了求解数学模型的启发式算法。

(3) 采用仿真实验，评估了不同W-SDN流表数量约减方法的性能，并证明了本文提出方法的可行性和有效性。

1 无线软件定义网络中的流表约减

从逻辑上讲，W-SDN主要由一个中央控制器和一些SDN使能的节点组成。通过中央控制器根据标准SDN范式安装的流表，每个节点可以实现针对每流的可控性。通过这种机制，每个节点的控制功能集中在中央控制器中，因此控制平面和无线网络的转发平面是分离的，而这种分离机制能够为无线通信网络带来网络的可全局视图、网络可编程性、网络可虚拟化等好处。无线软件定义网络(W-SDN)是SDN技术在包含多个无线和有线网络的无线异构网络中的应用，其基本结构如图1所示。目前，已经存在多种W-SDN架构或项目，如SoftCell[8]、SoftRAN、MobileFlow、OpenRadio[9]等。但是，这些架构均没有关注减少无线节点中流表数量的重要性。为了解决这个问题，本文提出了一种称为LSP重用的新机制。

图1 W-SDN的体系结构

1.1 示例说明

如图2所示，我们首先用一个例子来说明LSP重用的工作机制。

(a) 无线网络拓扑以及两条LSP

(b) LSP重用的工作过程图2 LSP重用机制的示例网络

假设一个无线网络如图2(a)所示。有两个LSP是LSP1：LER2→LSR2→LSR3→LER4和LSP2：LER1→LSR1→LSR2→LER3。我们假设有一个新的流从LER1传输到LER4。但是，没有LSP连接LER1和LER4，因此需要使用LDP、RSVP等建立新的LSP。因此，随着流量的增加，LSP的数量将会扩大。LSP的数量可能会达到n2，其中n是标签边缘路由器(LER)的数量。我们认为，通过LSP重用技术可以有效降低网络中需要的LSP，因为LSP可以被不同目的地的流共享。如图2(b)所示，在启用Openflow的LER1中，两个MPLS标签被堆叠到数据包标头中。最外面的标签沿着LSP1发送分组，而第二层标签沿着LSP2发送分组。我们将阈值设置为4。基于Openflow提供的数据包编辑能力，最外层标签的TTL设置为6，内层标签的TTL设置为6。当数据包从LER1传输到LSR2时，沿着LSP2交换机的路由器最外面的标签如图2(b)所示，当数据包到达LSR2时，最外层标签的TTL减少到4，LSR2脱去最外层标签，并露出内层标签。因此，LSR2检查内层标签并通过LSP1传输数据包。然后沿着LSP1的路由器交换内部标签，直到数据包达到LER4。从以上例子可以看到，在传统情况下，需要安装4个新的流表项来完成从LER1到LER4的传输。但是，使用LSP重用技术，可以使用LSP2和LSP1的片段来完成整个端到端传输，因此不需要安装新的流表。

1.2 LSP重用

标签交换路径(LSP)指的是在MPLS(Multi-Protocol Label Switch)网络中，由包头中MPLS标签标识的一条已建立的逻辑隧道。由于Openflow协议完全支持MPLS操作，如标签压入，弹出和交换等，因此我们可以将MPLS和LSP直接部署于W-SDN，而无需对软件或硬件进行任何修改。使用LSP传输数据类似于源路由，但每个无线节点维护的状态信息(也就是流表数量)不低于使用分布式路由协议的状态信息，因为它必须建立n2条LSP来实现整个网络的互联，其中n是网络中标签边缘路由器(LER)的数量。我们对传统的MPLS转发模式进行了修改，并通过在数据包报头中嵌套多个标签并利用TTL弹出最外层标签实现了一种LSP重用机制。LSP重用机制主要需要执行三个功能：

1) LSP规划 LSP规划过程由中央控制器执行，而非采用传统的LDP或RSVP协议。LSP规划过程的目标是用尽可能少的LSP覆盖整个网络。

2) 路由编辑 路由编辑功能主要在中央控制器和网络边缘节点上执行。路由编辑的主要任务是将MPLS标签压入数据包报头并设置标签的TTL值。根据用户需求和网络状况，路由计算由中央控制器或分布式路由算法完成，并通过Openflow协议以流表的形式发送并安装到流量流入的网络边缘设备。之后，包头编辑过程在该设备处完成，如图3所示。

图3 数据包头部中的标签编辑流程与流表结构

3) 分组转发 该过程主要在中继节点或基站进行。但是，与传统的MPLS报文转发不同，我们设置TTL阈值来弹出MPLS标签。正常情况下，路由器按照最外层标签转发数据包，当标签的TTL等于阈值时，路由器将弹出最外面的标签。继续按照下一层标签转发数据包，直到数据包到达目的地。处理流程如图4所示。

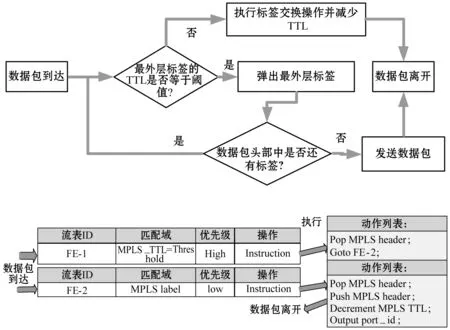
图4 数据包转发过程中的标签和TTL处理流程与流表结构

这一转发逻辑可能需要对传统的网络设备进行更改，或引入Openflow的支持来实现。然而，通过最终的实验仿真结果，我们认为这些开销与成本与LSP重用方法带来的改进相比是值得的。

2 LSP规划问题优化模型

(1)

目标函数表示优化模型希望最小化LSP集合中所有LSP的总长度，以便在给定的LSP数量下，网络中所需的流表数量能够最小。

(2)

式(2)保证网络的每个链路至少被一个LSP覆盖。

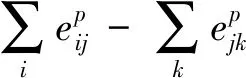
∀p∈S,∀(i,j)∈E,∀(j,k)∈E

(3)

式(3)确保每个LSP都是连续的。

(4)

(5)

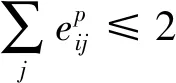
(6)

式(4)-式(6)保证了LSP无环路。为了找到包含最少LSP的集合P，我们需要让|P|从0增长到|E|，并针对每个给定的P求解上述数学模型。但是，由于数学模型中的变量是|P|×|N|维的，因此在大规模网络场景中，计算复杂度会较高，然而LSP规划过程一般需要快速完成，以防止网络发生链路故障或路由变化等时业务中断，因此需要提高LSP规划算法的效率。出于这个原因，我们提出了一个启发式算法，解决LSP的最优规划问题。算法的基本思想是，在每次迭代中，规划一个无环LSP，使其可以覆盖尽可能多的未覆盖的链路，直到所有链路都被LSP覆盖。该算法的伪代码如下所示:

算法1LSP规则

Input: overlay,topology;

Output:P;

1:booleanstop=false;booleanloop=false

2:whilestop!=truedo

3:forsource=0to|V|do

4:whileloop!=truedo

5: loop=true;

6:forj=0to|V|do

7:fork=0 to |V|do

8:ifnodekandjareconnectedandtheroutefromsourcetokdoesn’tcontainnodejthen

9:ifcover(source,k)+cover(k,j)

>cover(source,j)then

10: route(source,j)=

route(source,k)+route(k,j)

11:endif;

12:endif;

13:endfor;

14:endfor;

15:ifthereisanyroute(source,j)ischangedthenloop=false;

16:endif;

17:endwhile;

18:endfor;

19:findtheoptimalrouteandupdatetheoverlaytopologywiththeoptimalroute;

20:ifalllinksarecoveredthenstop=true

21:elseifstop=false;

22:endif;

23:endwhile;

在算法中，我们使用两种拓扑：覆盖拓扑和连接拓扑。前者表示链路是否被LSP覆盖，后者表示网络中每个节点的连通性。在算法的过程中，覆盖拓扑将不断更新，但连接拓扑将保持不变。从第4行到第17行的循环中，我们使用动态规划从图中找出从源到任何终点(LER)的最佳路径，该路径能够覆盖最多的未覆盖链路。然后，通过从第3行到第18行的循环，我们计算每个点的最佳路径，并找到覆盖当前图中大多数链路的最佳路径。每次我们计算出最优路径后，我们根据最佳路径删除覆盖拓扑中选定的链路，如第19行所示。当所有链路被LSP覆盖时，算法停止(第20-21行)。

3 实验仿真

在本节中，我们使用仿真实验来评估所提出方法的性能。不失一般性，我们在仿真中使用n×n矩阵网络拓扑，如图5所示。

图5 仿真实验拓扑图

我们选择的比较方法是多点对点隧道合并方式(MP2P)[10-12]，这是最常用的转发表约简方法；以及Splano等提出的MPLS网络中最新的转发表约减方式—非对称合并隧道方法(AMT)[13-14]。图6给出了不同路由数目的情况下，网络所需的最小流表数量。

图6 不同路由数量下的流表数量

根据图6所示，流表数量随路由数量的增加而增加，但是无论路由数量多少，采用LSP重用方法总能达到最小的流表数量。同时，随着路由数量的增加，LSP重用相比于其他方式的优势逐渐扩大。当路由数量为100时，与MP2P合并相比，LSP重用可以将流表数量减少71.9%，与AMT方法相比，可将流表数量减少58.3%。之后，我们评估不同网络规模下不同方法的性能。

路由数量设置为100，不同网络规模下的流表数量如图7所示。从图7中可以看出，随着网络规模的增加，所有三种方法的流表数量都会增加。同时，LSP重用方法在任何网络规模下始终能够达到最小的流表数量。因此可以证明，本文提出的方法具有良好的可扩展性，可以应用于大规模无线网络。除了减少网络中流表数量之外，我们还希望流表数量的分配尽可能均匀，以避免在某些特定节点处安装太多流表，从而导致性能或能耗瓶颈。

图7 不同网络规模下的流表数量

图8显示了采用三种不同方法时的流表数量分配情况，从图8的结果可以看出，LSP重用方法不仅可以实现最小的流表数量，而且可以实现比其他方法更加均匀的流表分布。

(a) MP2P合并方法 (b) 非对称合并隧道方法 (c) LSP重用图8 采用不同方法时的流表数量分布

此外，当使用LSP重用时，数据包头的长度等于仅在最坏情况下等于使用源路由方法时的长度。所以LSP重用导致的带宽浪费比源路由造成的带宽浪费要小得多。在不同最大包长的情况下，两种方法造成的带宽浪费如图9所示。

图9 不同包长下的带宽浪费比率

那么可以得出这样的结论：LSP重用可以实现类似于源路由的路由控制能力，而只需要更短的头部长度。

4 结 语

本文研究了W-SDN中的流表数量约减问题，提出了一种基于MPLS网络中LSP概念和Openflow网络编程能力的LSP重用方法。通过在数据包头部中嵌套多个MPLS标签并设置这些标签的TTL值，我们可以控制数据包在不同的LSP之间切换，以便利用不同LSP的片段来完成端到端的传输。因此，以流表形式存储的状态信息可以显著减少。通过仿真和实验，证明本文提出的方法能够以很小的流量开销实现最佳的流表约减效果。