读者驱动资源建设中预测算法的研究及应用

鲁 萍 张骏毅

1(西安建筑科技大学理学院 陕西 西安 710055)2(西安建筑科技大学图书馆 陕西 西安 710055)

0 引 言

基于读者借阅相关信息的决策资源建设方案作为图书馆一种新型资源建设模式近年来成为研究热点。将读者的阅读需求量化成一定指标，并以此确定购入的文献[1]。其中读者的借阅记录是体现读者需求的一个重要因素，也是影响未来资源建设策略的关键指标。通过对已掌握数据的分析，建立一套行之有效的预测机制，从而对读者未来的阅读需求做一个科学合理的预判。研究基于已有的借阅记录预测未来的借阅情况，可以为资源建设提供合理参考[2]。目前的研究多限于粗线条的框架，对细节研究较少，如具体的预测算法以及影响因素分析等[3]。本文基于数据特征分析，建立了不同周期模式下的预测机制，分别探讨BP神经网络模型和GM(1,1)模型的应用，对比分析后得到关于预测机制的合理建议。

1 数据分析

通过对馆藏流通规律的分析,利用三年前入藏图书的借阅记录作为分析样本,在此基础上建立图书采购模型最为合理[4]。以西安建筑科技大学图书馆2013年-2015年的读者借阅数据为样本数据进行研究分析。按照中图分类号对图书各个分类数据进行整理，因数据庞杂本文仅以TU类(建筑科学)为例。除去2月和8月的寒暑假期，一年的有效借阅数据为10个月。以月为单位对读者借阅人次的数据进行统计如图1所示，上下浮动变化较大，明显是非单调变化。以学期为单位统计读者借阅人次如图2所示，大体呈线性变化。

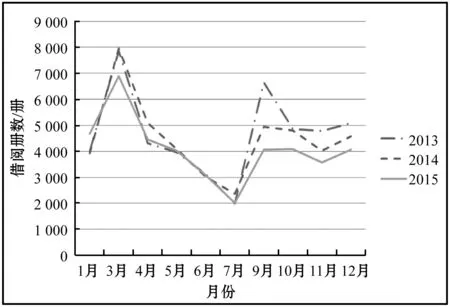
图1 TU类按月读者借阅人次统计

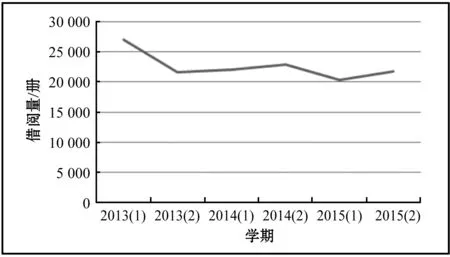
图2 TU类按学期读者借阅人次统计

BP神经网络模型和灰色系统模型均可用于研究数据规律并进行预测。BP神经网络模型适用于呈现非线性的大量数据的预测和分析，而灰色系统模型适用于数据量小，趋近于线性变化的波动较小的数据[5]。结合上述读者借阅数据分析，在不同时间跨度上进行预测可以选用不同的模型。以月为单位进行预测选用BP神经网络模型，以学期为单位用灰色系统模型。

2 BP神经网络预测模型

2.1 BP神经网络模型

BP神经网络是一种具有多层感知器的前馈网络，网络含有输入和输出结点以及一层或者多层隐含结点，采用误差反向传播的学习训练算法调整连接权。BP神经网络的训练过程：选择一组训练样本，样本中包含输入信息和期望的输出结果；从训练样本中取一个样本，把样本中的输入信息输入到网络模型中；分别计算经神经元处理后的各层结点的输出值，计算网络的实际输出与期望输出的误差；如果误差达到要求，则退出，否则继续执行下一步。从输出层反向计算到第一个隐层，按照能使误差减小的原则调整网络中各神经元的连接权值和阈值，对训练样本集中的每个样本都执行前两步的操作，直到对整个训练样本集的误差达到要求为止[6]。

本次选取2013年1月到2015年 12月建筑科学(TU)的30组数据作为训练样本。其中，前25组数据用于BP神经网络学习训练，后5组数据用于预测误差分析。设置最大训练次数为5 000次。

Step1输入训练样本。

输入样本P=[1,2,…,30]，其中1,2,…,30分别表示2013年1月到2015年12月对应的时间序列。需要对神经网络的输入输出数据进行归一化处理。

Step2创建初始的神经网络。

设置神经网络的训练参数，设置最大步长、神经网络的学习率以及误差指标。

Step3进行神经网络训练，并对训练好的网络进行误差检验。

Step4进行仿真预测。

产生输入数据，对输入数据做归一化处理，进行数据预测。本次计划预测未来1年内的10个数据，便于2种预测模型进行误差对比。

基于神经网络模型进行预测，得到2016年1～12月的10组数据。以1月为例，如图3所示。

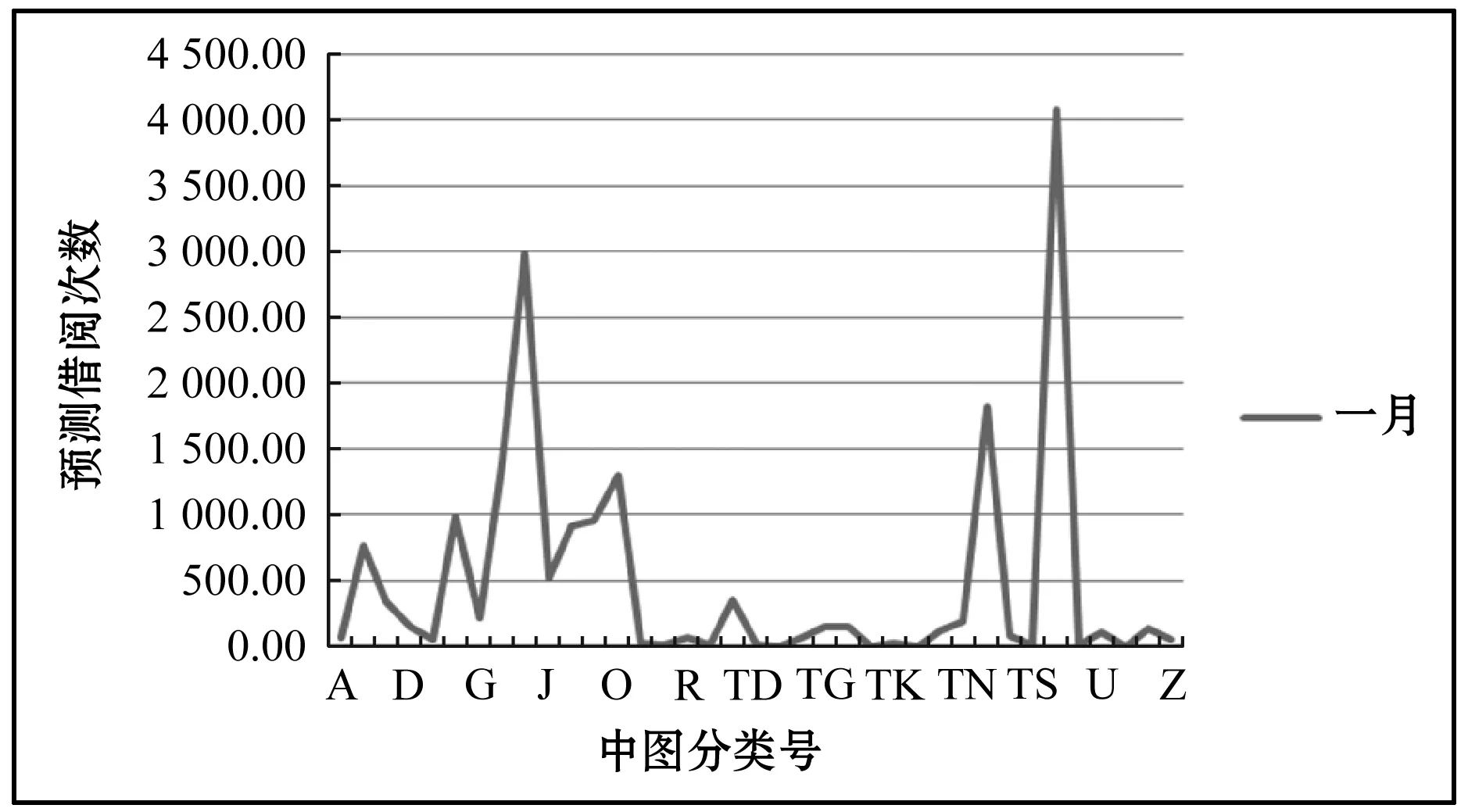
图3 基于BP神经网络模型的预测结果

2.2 相对误差分析

对每类数据进行误差分析，用2016年中有效的10个月数据进行数值计算，利用预测值和真实值计算平均误差，定义误差公式如下：

(1)

式中：aik表示第i类图书第k个月借阅人次；gik表示第i类图书第k个月的累计借阅人次的预测数据，其中k=1，2，…，N分别表示2016年N个月；εi定义为第i类图书的平均预测误差。

依据式(1)，计算得到各类图书的平均误差值如图4所示。对比原数据和仿真数据可以看出平均相对误差几乎都在合理范围之内(<10%)，说明预测效果比较理想。利用该模型可以合理预测出未来一年每月的读者借阅人次。预测数据可以为决策模型的建立提供可靠的基础数据。

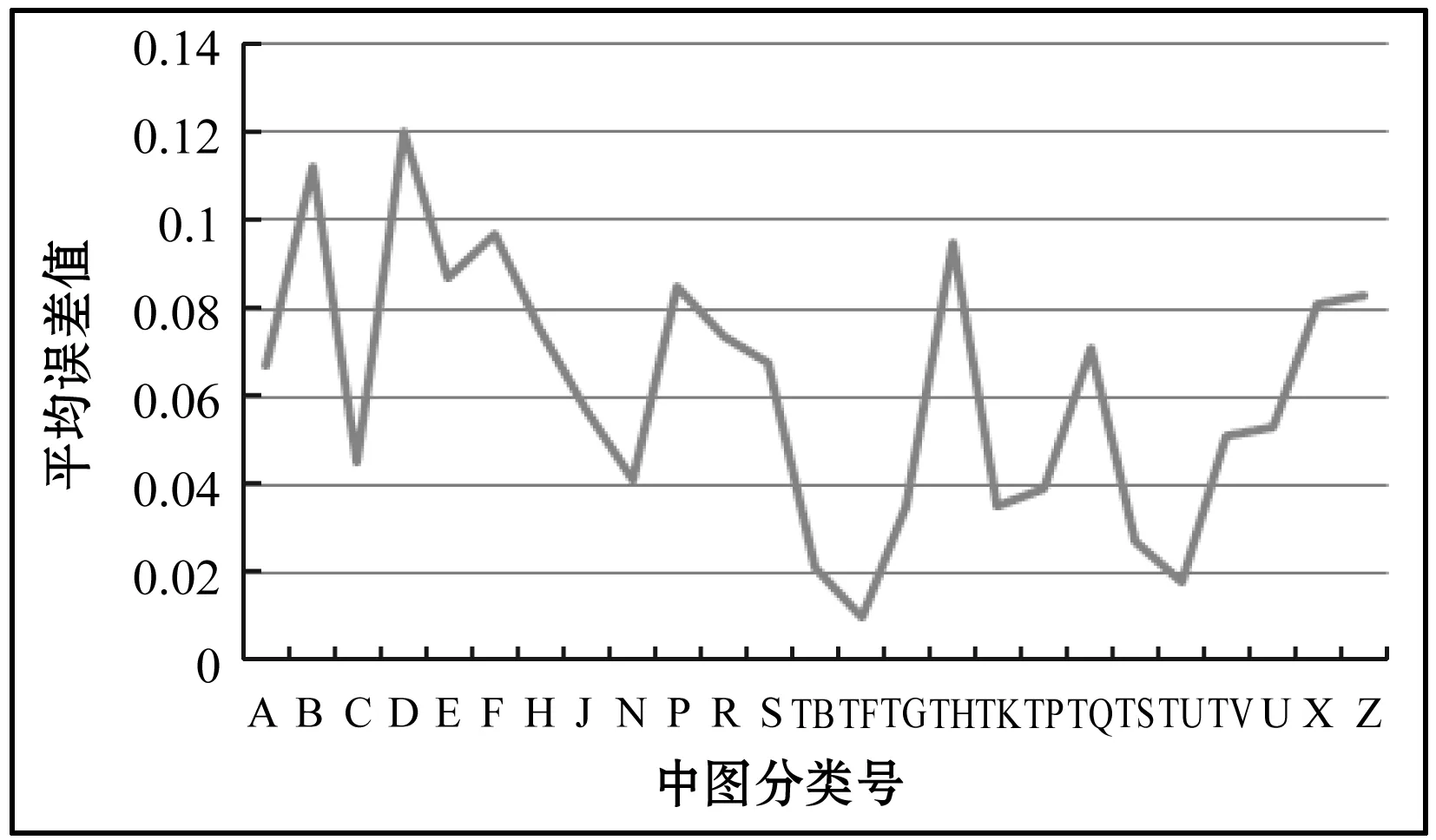
图4 BP神经网络模型预测平均相对误差

3 灰色预测模型

3.1 构建GM(1,1)预测模型

灰色预测模型常用于少量数据、短期内的预测。对读者借阅人次按照中图分类法以学期为单位进行划分，得到每一类6个数据，去除了假期的影响，同时避免存在孤点影响数据的整体预测效果[7]。由于预测分组较多，无法对每一组数据进行一一说明，本次预测以TU类数据为例，构建基于GM(1,1)的借阅预测模型。

Step1检验数列的非负性。对原始数据X进行累加处理，得到单调的序列数列S。

由TU类原始数据得到S=[2 7057 48 654 70 672 93 537 113 873 135 647]。

Step2检验数列S是否满足准光滑性。对累加数列S依照式(2)做光滑性检测，求出满足准光滑条件的最小k。

(2)

其中：X原始数据列；S是累加数据列。

在对S做光滑性检测得到：ρ(k=2)=0.79,ρ(k=3)=0.45,ρ(k=4)=0.32。显然，当k等于3时ρ(k)<0.5，所以当k>2时，准光滑条件满足。

Step3作紧邻均值计算，生成新的数列Z:

(3)

将数列S代入并做紧邻均值生成，得到数列Z=[37 860,59 660,82 100,103 710,124 760]。

(4)

(5)

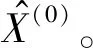
通过2013年到2015年的读者借阅数据建立的灰色预测模型得到2016年的按中图分类号划分的每学期数据如图5所示。

图5 基于GM(1,1)模型的预测结果

3.2 相对误差分析

使用2013年到2015年按学期划分的数据建立灰色系统预测模型。计算出2015年两个学期读者人次预测结果，对依照中图分类的每类数据进行综合误差分析，利用预测值和真实值计算整体误差，定义误差公式：

(5)

其中：bi表示第i类图书2016年1月到6月的累计借阅人次；gi表示第i类图书2016年1月到6月的累计借阅人次的预测数据；μ为各类图书的平均权值预测误差；N表示图书种类数。

用西安建筑科技大学2016年1月到6月的数据进行计算得到结果μ=0.077 9，说明预测合理。图6显示了对每一类图书的平均相对误均在10%左右，预测效果相对比较满意，可以作为决策模型的一个依据。

图6 GM(1,1)模型预测结果的平均相对误差

4 结果分析

4.1 横向误差比较

对BP神经网络预测模型和GM(1,1)预测模型的预测结果进行分析。首先需要统一度量标准，将BP神经网络算法中按月时间周期转换为按学期的时间周期，再与GM(1,1)模型误差进行横向对比[8]。具体步骤如下：

Step1利用BP神经网络得到按月的每一类拟合值之后，将拟合值按着每学期的时间序列进行累加，得到BP神经网络的按学期的拟合值，对其进行相对误差计算[9]。

Step2利用灰色系统得到按每学期划分的时间序列的拟合值，对拟合值进行相对误差计算。

Step3对转换成相同时间序列的相对误差进行横向比较。

由图7对比两种预测模型得出的结果后，发现这两个结果之间的相对误差都在5%左右，从而更加验证了使用两种预测模型的合理性和正确性。

图7 两种方法误差比较

4.2 纵向误差比较

通过重新分割数据，选取部分数据作为预测方法的训练数据用于建立模型，选取剩余数据作为样本真实值，分别计算未来3组数据、2组数据以及1组数据的预测误差。由表1和表2数据可知。对未来1组数据，BP神经网络预测算法误差小于GM(1,1)预测误差，即预测的准确性更高。对未来第2组数据，GM(1,1)的预测误差小于BP神经网络算法，但是二者的误差都较大，已经不适用于进一步使用。未来第3组数据误差非常大。由此可知，BP神经网络算法和GM(1,1)算法都可以用于预测未来一学期的各类图书借阅人次，BP神经网络算法整体误差低于GM(1,1)算法。用待预测学期之前临近的数据可以提高预测的准确性。

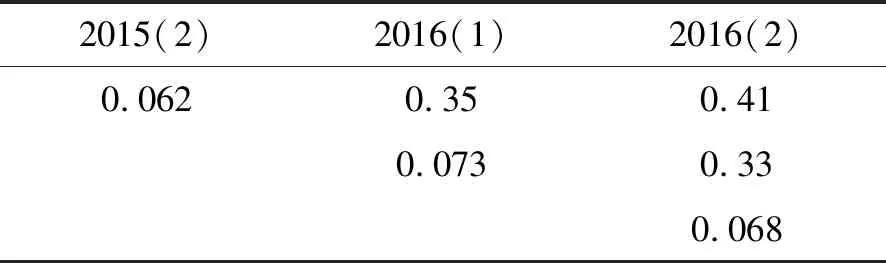
表1 BP神经网络算法预测误差

5 结 语

基于读者信息的图书馆资源建设策略需要对已有数据进行分析，使用合理的预测方法对资源需求进行预测。本文对图书馆近三年的读者借阅数据进行分析，依据数据以月为周期和以学期为周期的不同规律，分别使用了BP神经网络模型和GM(1,1)模型对读者借阅人次进行预测。对每种方法分析了结果误差，最后进行综合对比分析，给出了关于两种预测方法的使用的合理化建议，用于指导未来一学期的建设计划。根据实际需求，还可以进一步改进算法，使预测结果更加准确合理。在资源的多样性预测方面可进一步讨论，为图书馆的资源建设综合策略提供有力的支持[10]。