小波阈值去噪在盾构偏离趋势预测中的应用

路 祥 佟国香

(上海理工大学 上海 200093)

0 引 言

随着我国地铁建设事业的快速发展，在城市隧道中采用盾构法施工越来越普及。盾构法建造隧道要达到建后的隧道轴线与隧道设计轴线误差不大于允许偏差的范围这一目标，故盾构推进施工的关键技术是盾构轴线控制的技术[1]。实际的施工过程中，由于地质情况变化、盾构旋转等因素的影响，需要在施工中不断进行姿态修正，来保证盾构机前进路线相对于隧道设计轴线的偏差在允许范围内[2]。

施工中需要实时获取盾构机姿态变化情况来判断是否需要对盾构机的姿态进行调整，而盾构机的姿态数据则是由传感器获取的直接数据进行计算之后得到的。在实际施工中，由于复杂的环境因素对传感器的影响，传感器数据计算出的盾构机姿态可能会与实际姿态存在一定的偏差。这一结果可能会影响施工人员对盾构机姿态进行及时修正，从而导致盾构机运行轴线与设计轴线偏离。当发现偏差后要及时对盾构机姿态进行纠偏，偏差量较小时可以选择合适管型和安装点位进行纠偏，超过管片纠偏范围时就要设计纠偏曲线[2]。目前比较成熟的纠偏曲线有三次抛物线和连续的反向圆弧两种[3-4]。所有的纠偏都会增加施工中管片的安装难度，并且纠偏曲线的设计也必须非常精确，否则可能造成实际纠偏过度而产生蛇形掘进，蛇形掘进不止影响管片的安装还会造成对地层的过量拢动。

因此，在施工中应尽量避免发生较大的盾构机偏离，这就需要对盾构机的姿态进行较准确的预测。本文提出通过去噪后的盾构机姿态数据实现对盾构机偏离的预测，从而避免在施工中发生较大偏离，并通过实验对预测效果进行验证。

1 盾构偏离预测处理机制

盾构机中的传感器获取到的行程数据进行一定的计算后可以得到盾构机的偏离角，然后对得到的偏离角进行去噪处理，最后通过去噪后的偏离角实现对盾构机的接下来的偏离情况进行预测。步骤流程如图1所示。

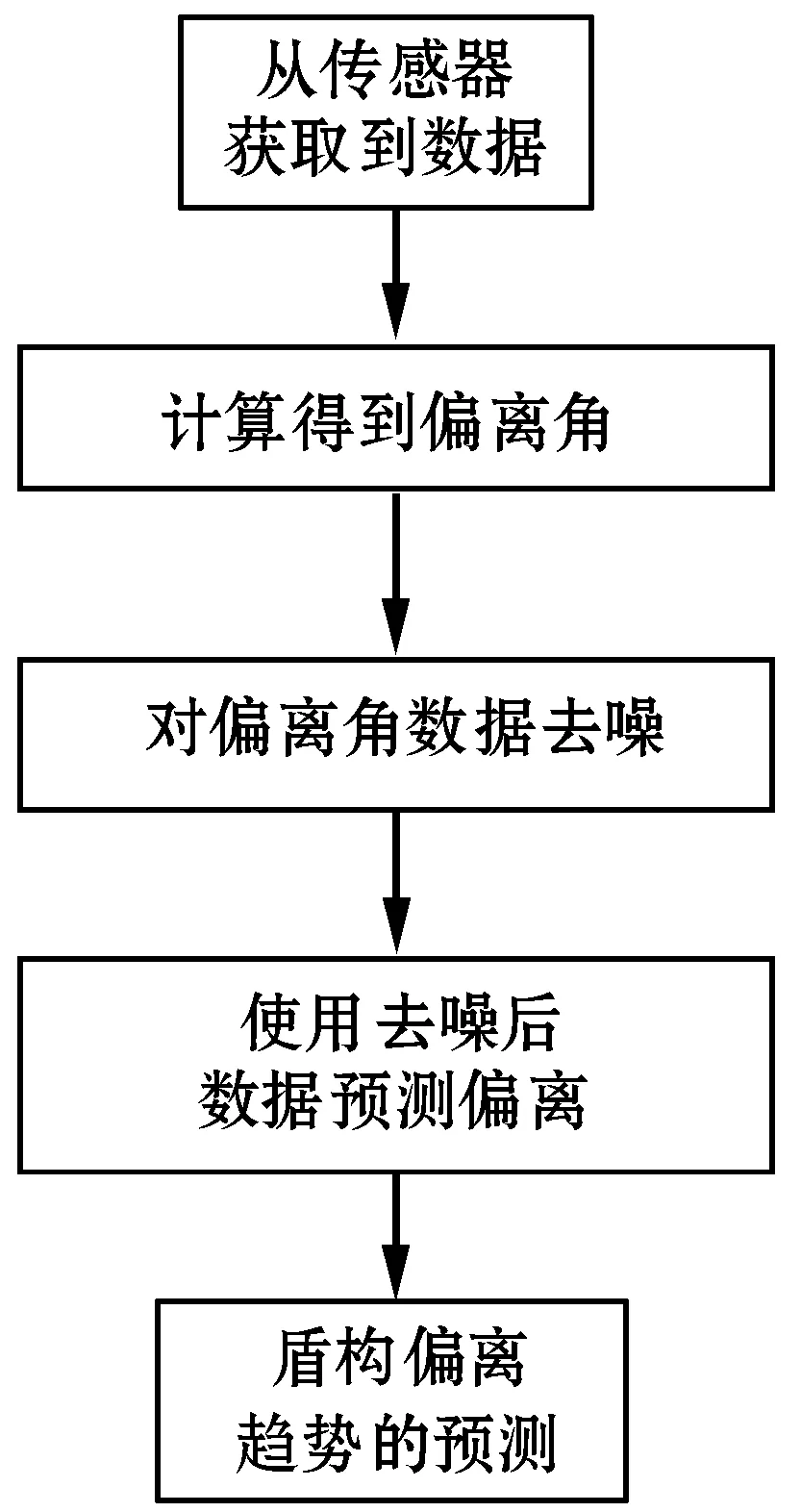
图1 偏离趋势预测流程图

1.1 计算偏离角

以某品牌盾构机为例，此盾构机中千斤顶每3个为1组，每3组或4组千斤顶构成1个区，共计19组千斤顶，6个分区。计算步骤如下:

1) 设每组千斤顶传感器的空间坐标(xi,yi,zi)，其中i为1到6之间整数，可得：

Xi=li

(1)

yi=Rsinθi

(2)

zi=Rcosθi

(3)

式中：li为第i组传感器记录的位置；R为千斤顶分布圆半径；θi为第i组千斤顶对应的圆心角。

2) 设盾构机千斤顶前进的方向向量为(x,y,z)，可得：

(4)

式中：

a12=a21=∑xiyia13=a31=∑xizi

a32=a23=∑ziyi

c1=∑xi，c2=∑yi，c3=∑zi

解此三元一次方程组即可得(x,y,z)。

3) 计算方向角

盾构相对管片水平方向夹角αy：

(5)

盾构相对管片垂直方向夹角αz：

(6)

此时得到的αy和αz即为盾构机的偏离角。

1.2 盾构偏离趋势预测

(1) 盾构偏离角数据去噪：计算得出的盾构机偏离角数据由短时高频分量和长期低频分量组成。小波变换则适用于分析这种类型的信号，通过分解原始信号中包含的不同频率部分，来消除信号中包含的噪声，获得最接近真实值的最优估计结果。

在所有的小波函数中，当具有时频紧支性、高正则性、正交性等优点的Daubechies小波作为小波函数时，在信号去噪方面有较好的效果。在去噪方法中选择去噪效率高且去噪效果好的小波阈值去噪法。综上所述，选择基于Daubechies小波函数的小波阈值去噪法对数据进行去噪分析。

① 分解尺度 对于任意一个信号来说，都存在一个去噪效果最好或较好的分解层数，所以分解层数的选择对于信号的消除噪声的效果影响很大。通常情况下，若信号的分解层数选择过高, 会对所有的各层小波空间的系数都进行阈值处理，这样反而会导致消噪之后信号的信噪比下降。反之如果分解层数过低则会导致信号的噪声消除效果不明显，信噪比提升不多。综合考虑去噪效果和去噪所需计算量，选择分解尺度为三层。

② 阈值选取 阈值的选择方式将会影响到信号去噪后的信号变现，阈值选择方法有：固定阈值估计、无偏似然估计、极值阈值估计以及启发式估计4种。实验中将会对这4种阈值选择方法的实际去噪结果进行比较，根据实际的去噪效果选择适合的阈值选择方法。

(2) 偏离趋势预测方法：在不改变千斤顶组推力情况下，可以视作盾构机做相对稳定的曲线运动，此时可通过数学方法得到盾构机偏离角的变化函数。盾构偏离角的变化函数的拟合采用计算量小且拟合效果好的二次多项式，多项式原型如下：

y=a0+a1x+a2x2

(7)

通过最小二乘法得到上述a0、a1、a2之后，就可以得到偏离角的变化函数，通过此函数就可以达到预测偏离变化趋势的目的。

2 实验仿真和结果分析

实验数据来源为上海市某段盾构法隧道施工的采集的现场数据，数据为盾构机水平方向夹角，详情见表1。实验中使用原始信号与去噪后的信号之间的偏差(BIAS)、均方根误差(RMSE)和信噪比(SNR)三种评估标准对实验结果进行评估，用于确定最终的阈值选取方法。

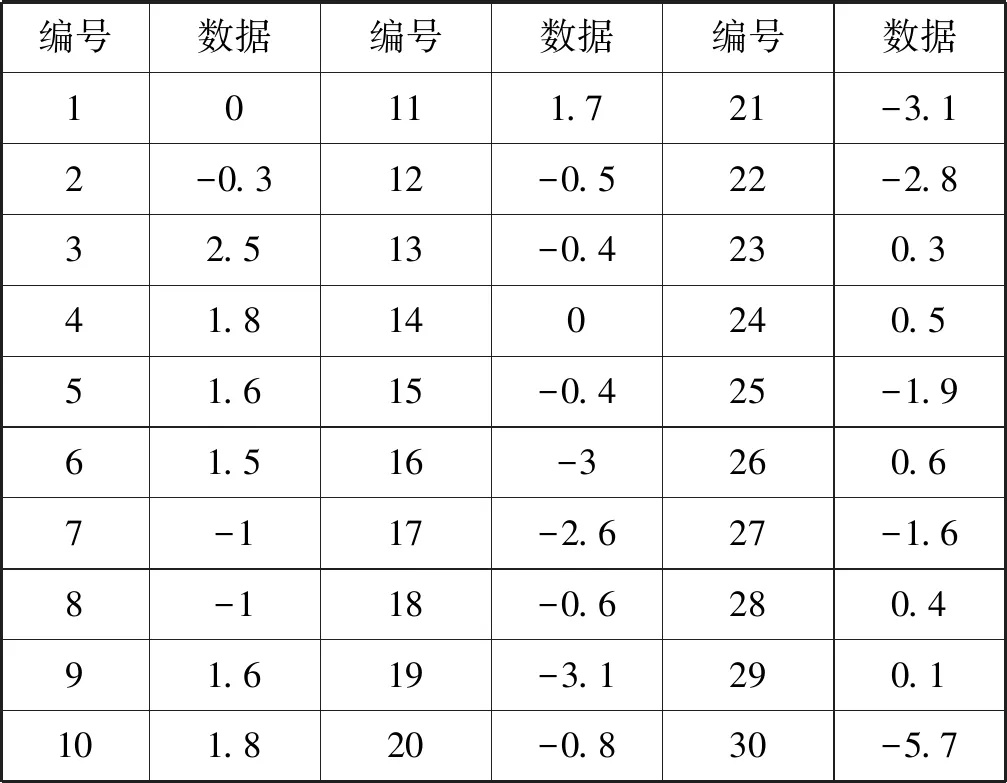
表1 盾构机姿态水平方向夹角 °

2.1 数据去噪

根据前面的分析，实验中采用Daubechies10作为小波函数，对应的小波分解层数为3层，以软阈值法作为阈值函数，阈值选取的方式将在下面的实验中选出最优方式。使用MATLAB中的小波工具箱对原始数据进行4种阈值法之后，去噪后的效果如图2所示。

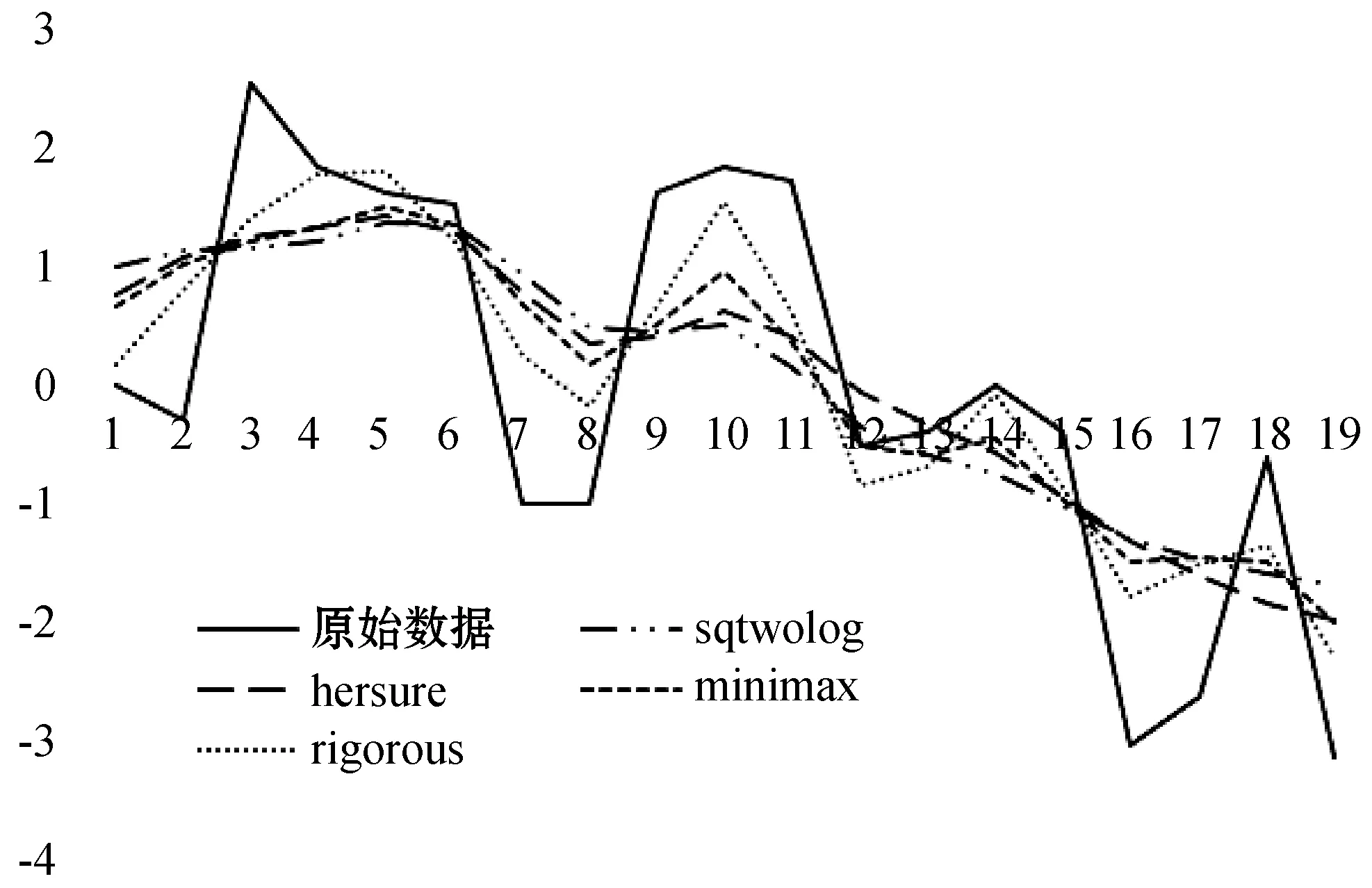
图2 阈值去噪对比效果图

首先根据图像进行初步筛选，sqtwolog和heursure阈值法得到的曲线较为光滑，去噪效果较好；而minimax和rigorous阈值法得到的曲线则相对较差，去噪后仍保留较多的极值，即保留了较多的噪声，噪声消除效果一般，所以通过初步筛选剔除这两种阈值法。下面使用部分去噪后数据详细分析sqtwolog和heursure阈值法的去噪效果，数据见表2，详细噪声消除效果指数见表3。

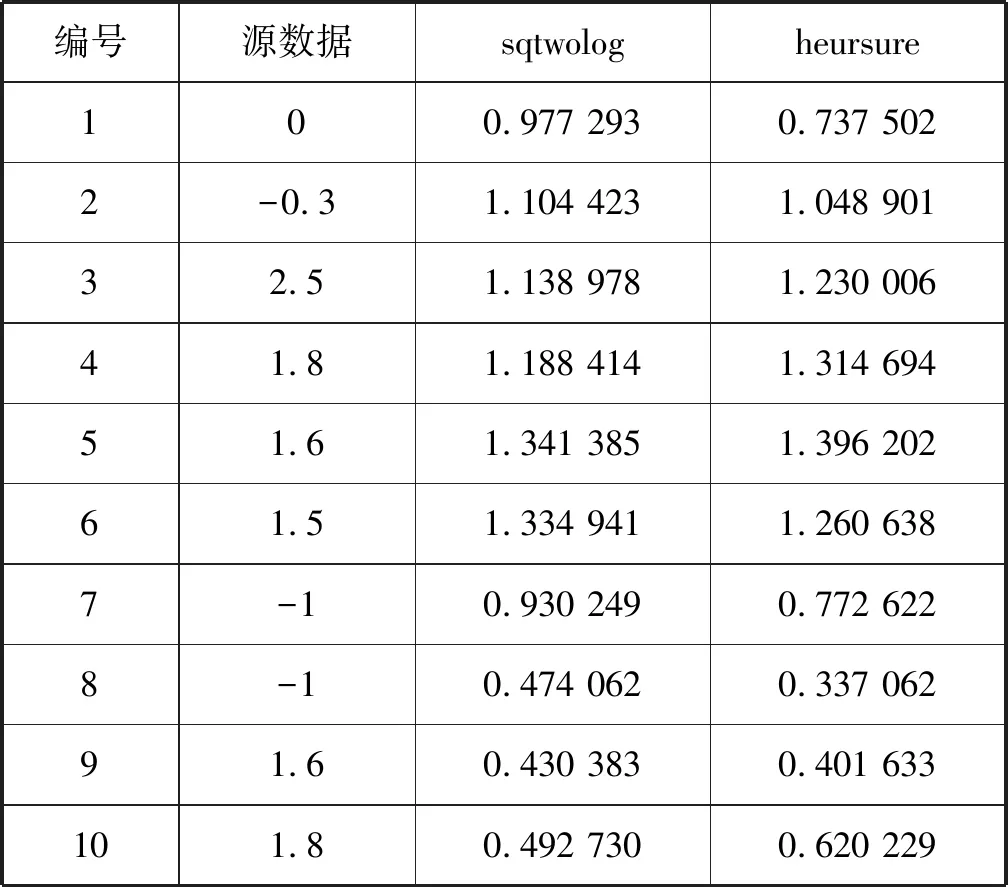
表2 去噪后数据

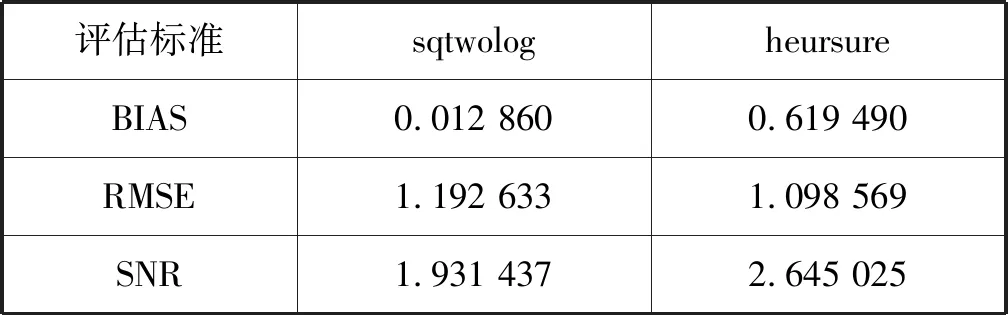
表3 数据评估结果

在三种评估标准中，RMSE值越小消除噪声效果越好，BIAS值越接近0消除噪声效果越好，而SNR值则是越大消除噪声效果越好。由此可知，两者相比，heursure效果明显优于sqtwolog。

由以上实验结果可知：去噪前，原始数据中存在较多的极值，数据整体规律性不强，很难通过数据获取到准确的盾构机姿态信息，数据可用性较低；在使用heursure阈值法去噪后，极值点减少，曲线变得光滑，数据可读性提高。

2.2 预测效果验证

当一组数据中的部分数据得到的偏离角变化函数，通过此函数对之后的数据进行预测，若预测值与实际数据较为接近时，则此组此偏离变化函数达到了预测的效果。

下面将验证去噪后的数据是否能够提高偏离角预测的准确性，将去噪后数据和原始数据分别用于偏离角预测，预测结果与实际结果的比较见表4。

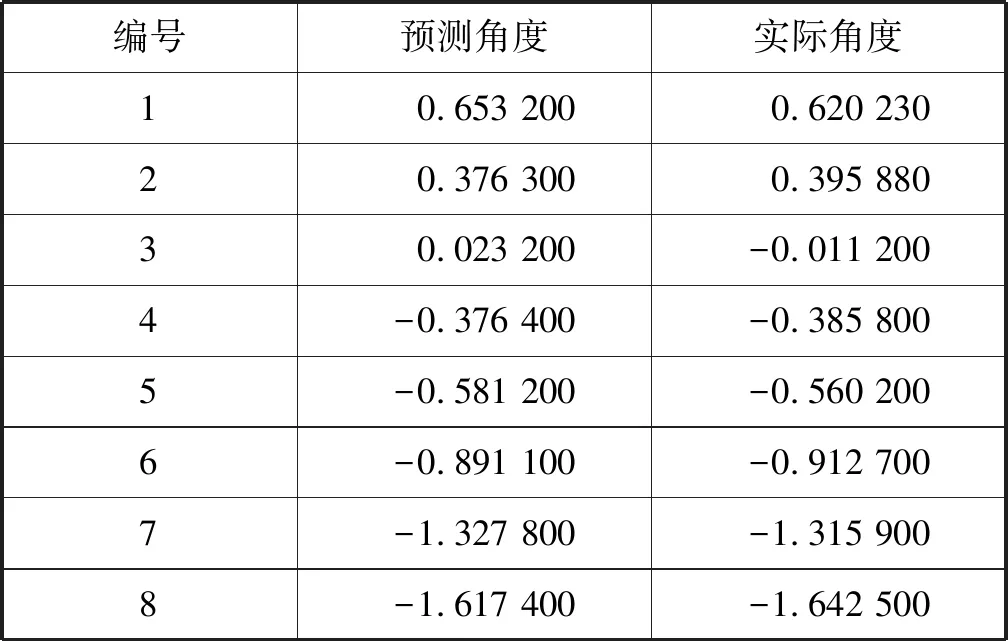
表4 预测角度与实际角度 °

通过表4可得，去噪后的数据通过拟合算法得到的偏离角预测值与实际的盾构机偏离角的差距较小，此时可以得到结论：去噪后的数据可以较为准确预测盾构机姿态。

3 结 语

通过传感器获取的原始数据计算的盾构机偏离，当误差较大时，将无法有效通过数据分析出当前盾构机的运行情况，从而导致盾构机偏离超过限定值而被迫通过纠偏线路进行矫正。本文提出使用Daubechies10小波去噪去除盾构机姿态数据中的噪声，通过二次多项式拟合得到盾构机姿态变化趋势的预测函数。实验结果证明此方法得到的预测函数能够满足施工中对姿态的预测要求，预测数据在盾构机姿态调整中有较大的应用价值。