改进的基于卷积神经网络的图像超分辨率方法

王 旺 徐俊武 李颖先

(武汉工程大学计算机科学与工程学院 湖北 武汉 430205)

0 引 言

图像的超分辨率SR(Super Resolution)技术，是通过软件算法来把低分辨率LR(Low Resolution)的图像转换成为高分辨率HR(High Resolution)图像的技术[1]。目前在许多重要的领域都十分需要这门技术的支持，例如在医学图像处理领域，高分辨率图像可以帮助医生掌握病情，看到人眼不易察觉到的病灶，可以更好地针对治疗[2]。

SR技术最早可以追溯到20世纪60年代，提出者为Harris[3]。当时的主流是方法是插值法，之后随着技术的发展，有新的方法被研究者提出，主要归纳为基于重建的方法和基于学习的方法[4]。插值法具有最简单的计算过程和最低的复杂度，常见的有邻插值法[5]、双线性插值法[6]和双三次插值法[7]；基于重建的方法在一段时间内颇为热门，经典的有迭代反投影法[8]、凸集投影法[9]和最大后验概率估计法[10]，这种方法最大的问题在于放大倍数有限，生成效果也不及后来者；基于学习的方法分为基于浅层网络的学习方法，主要有流形学习[11]和稀疏表示[12]；另一种基于学习的方法就是基于深度网络的方法。

将深度学习应用于图像超分辨率领域，最早由Dong等[13]提出，也就是经典的基于卷积神经网络的超分辨率方法(SRCNN)，之后不断地有学者进行优化和改进。

1 相关工作

1.1 基于卷积神经网路的图像超分辨率方法

基于卷积神经网络的超分辨率(SRCNN)方法是最先将深度学习引入图像超分辨率重建的问题。超分辨率方法将一张LR图像放大为一张HR图像，尺寸的变化造成像素点总量的变化，其中最难的挑战是如何在新增的像素位置进行值的填充。SRCNN使LR图像能通过一定的算法升为HR图像，主要是两者之间存在“共同特征”，所以在SRCNN中，将超分辨率过程分为三个阶段[14]：

(1) 特征提取。此阶段就是对LR图像进行特征提取和特征表示，利用卷积网络的性质提取图像块的特征，公式如下：

F1(Y)=max(0,W1×Y+B1)

(1)

(2) 非线性映射。将第一阶段提取的n1维特征映射至n2维，公式如下：

F2(Y)=max(0,W2×F1(Y)+B2)

(2)

(3) 重建。这个阶段是将第二阶段映射后的特征恢复为HR图像,公式如下：

F(Y)=W3+F2(Y)+B3

(3)

式中：W和B分别代表卷积模板和偏置参数。

SRCNN的网络模型结构如图1所示。文献[13]只使用了3层简单的卷积神经网络，分别进行上述三个阶段。

图1 SRCNN网络模型结构图

在SRCNN中，使用MSE作为损失函数，在图像输入前需要使用双三次插值放大至目标尺寸。此时虽然图像尺寸达到了，但是仍然称之为低分辨率图像，然后再进行输入。输出的是最终重建高分辨率图像。

1.2 优化相关技术

(1) 亚像素卷积层。亚像素卷积层[15]在输入原始低分辨率图像之后，经过卷积之后，得到通道数为r2的与输入图像大小一样的特征图像。然后将每个像素的r2通道再排列，成为r×r的区域，则每个像素都成为r×r大小，从而大小为H×W×r2的特征图像被重新排列成rH×rW的高分辨率图像。需要注意的是亚像素卷积层的输入维度为输出维度前r2倍，且r为放大倍数。

(2) 残差网络。通过加深网络的深度可以很好地提高网络的性能，但是可能会出现退化问题，随着网络层数的增加，在训练集上的准确率却饱和甚至下降。深度残差网络[16]的出现主要是为了退化的问题。

出现退化的原因，主要是因为神经网络在反向传播过程中要不断地传播梯度，而当网络层数加深的时候，梯度在传播过程中会逐渐消失[17]。

残差网络解决退化现象的原理如图2所示，将某一层的输入x直接传到后几层的输出中。这种方式被称为捷径连接，也就是最终的输出结果H(x)为原本的输出F(x)加上前几层的输入x，即：

H(x)=F(x)+x

(4)

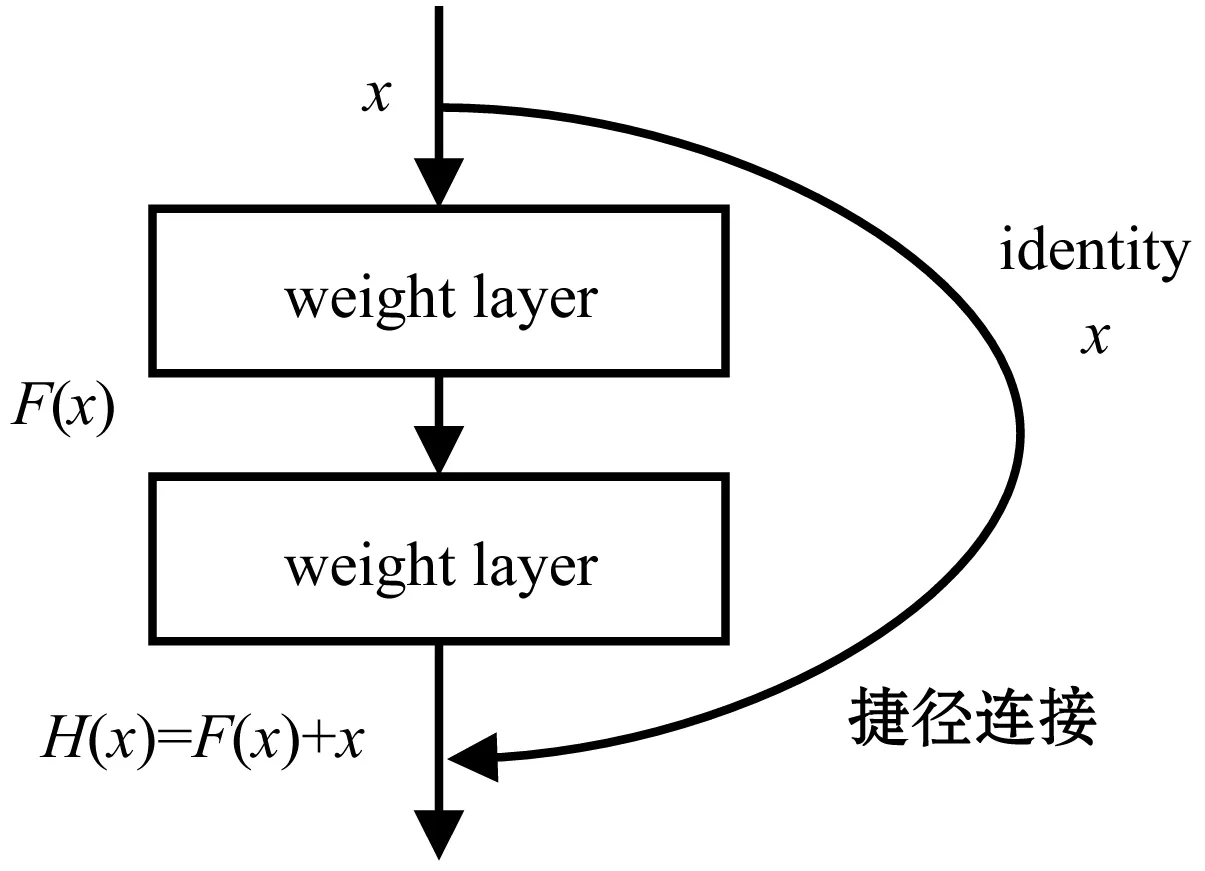
图2 残差网络示意图

这样做的好处在于，当F(x)由于退化问题变为0的时候，那么至少输出H(x)还是有值的。当H(x)=x的时候，被称为恒等映射，由于还有输出，那么梯度还可以继续传递。

同时在残差块中也会加入批量归一化BN[18]层，添加BN的最大优点是，减少梯度消失，加快收敛速度。根据研究表明，BN层需要添加在网络层后激活函数前[19]，效果最佳。

2 改进的SRCNN方法

本文提出基于SRCNN的图像超分辨率的优化方法，主要在SRCNN的基础上做出如下修改：

1) 在输入方面，本方法在最后以两层亚像素卷积层[20]的形式放大图像尺寸，因此可以直接将原始低清图像作为输入，而无需像SRCNN那样先以双三次插值的方式放大尺寸再输入。

2) 本方法还改变特征维数，使用更小的卷积核和使用更多的映射层，SRCNN总共只有3层网络，映射层只有一层，加深网络可以有效提升网络能力。

3) 本方法由于并非在网络外部进行放大图像的操作，所以更具有灵活性。当需要不同的上采样倍率时，只需要微调后面的上采样层就可以了，前面的映射层不变。

在SRCNN方法中，超分辨率的工作是在高分辨率的基础上完成的，这样并不是最优的办法，而且计算量很大。如果可以在网络内部进行超分辨率，通过训练学习将低分辨率特征映射到高分辨率输出，这样就能够减轻计算量，并且效果也更优。

在本方法中，网络模型可以分为3个部分：

1) 特征提取。SRCNN中的特征提取是对插值后的高分辨率图像进行提取，卷积核大小为9×9；本方法是直接对原始的低分辨率进行操作，因此可以选择小一些，设置为3×3。

2) 非线性映射。由于感受野大，能够表现得更好，在SRCNN中采用的是5×5的卷积核，但是卷积核大的计算量会比较大，用两个串联的3×3的卷积核可以替代一个5×5的。同时两个串联的小卷积核需要的参数数量为18，而5×5的参数数量为25，所以本方法使用多个3×3的小卷积层，兼顾计算量和网络能力。

3) 上采样。使用亚像素卷积层进行上采样。

具体流程描述如下：

1) 输入图像张量，维度为3；

2) 进入卷积层，输入维度为3，输出维度为64，卷积核为3×3，步长为1，之后接入激活函数ReLU；

3) 进入残差块，内部含有4个小残差块和一个卷积层，每个小残差块内部含有两个卷积层，每层卷积之后都加入BN层，激活函数为ReLU；

4) 进入卷积层，输入维度为64，输出维度为256，卷积核为1×1，步长为1，之后接入BN层，再激活函数ReLU；

5) 上采样卷积之前需要计算维度，先使用卷积层将维度升到一定高度再进行上采样，该卷积层输入维度为64，输出维度256，卷积核为3×3，步长为1，之后再进行上采样层，输出维度64，ReLU激活；

6) 再重复步骤5，两次上采样将图像尺寸提升4倍；

7) 最后以1×1卷积核降维到3，激活函数改为Tanh，输出大尺寸图像。

网络流程见图3。

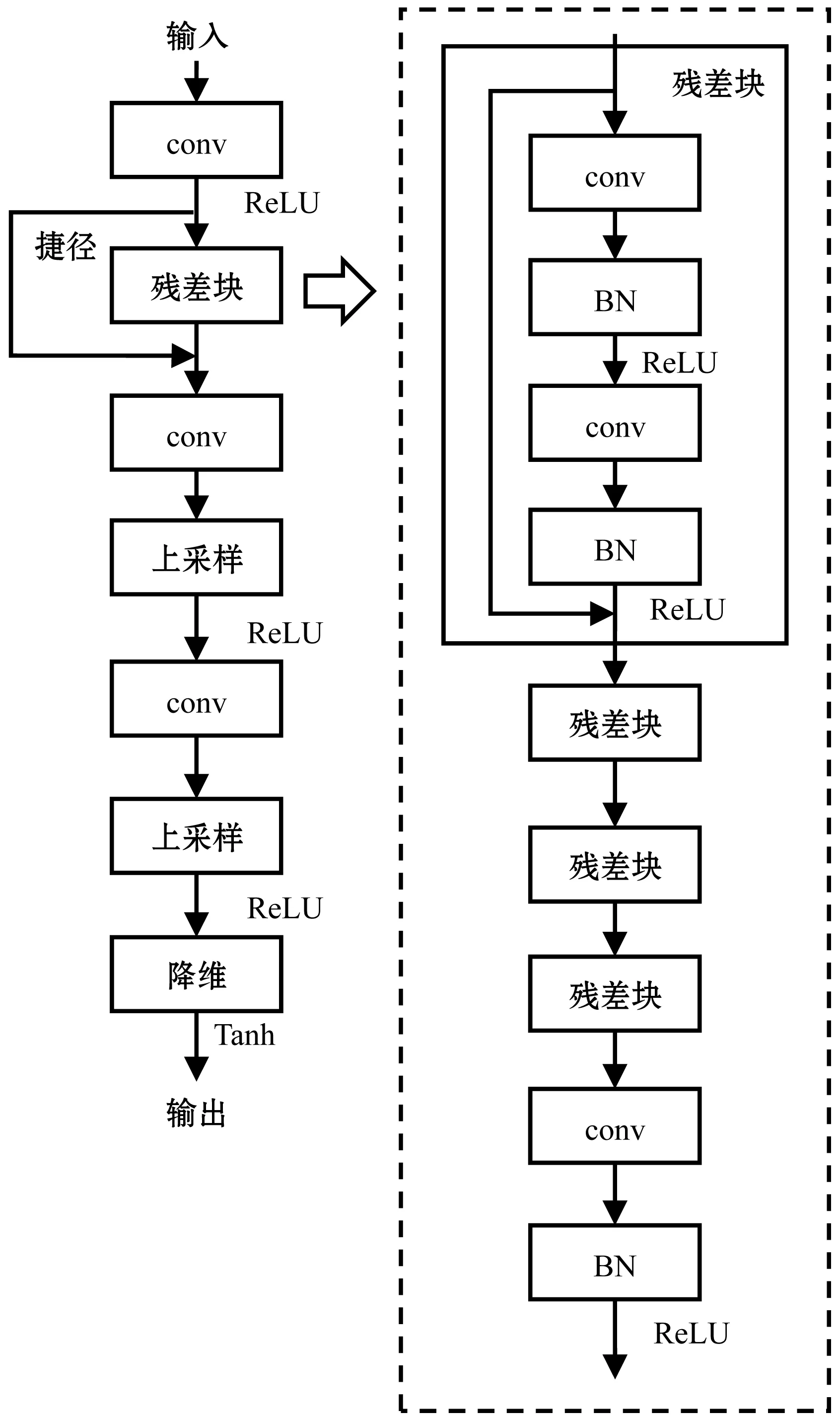
图3 本文方法网络流程示意图

在本文方法中，损失函数依然使用MSE，优化器选用Adam。

3 实 验

3.1 实验设计及评价标准

实验采用DIV2K数据集的图像作为训练集，训练完成后使用测试图像进行重建生成高分辨率图像用于查看效果。

由于实验中的低分辨率图像是从高分辨率图像进行1/4倍降采样得到，所以本实验有原始高分辨率图像作为对照。同时一起列出用双三次插值法重建图像；还另外用相同的训练集和训练次数训练SRCNN方法、ESPCN[20]方法和FSRCNN[21]方法并将测试图像生成结果一起列出。图4和图5分别展示这三种方法重建生成图像的结果和原始图像，都是截取了关键部分，以便查看细节部分。

(a) 双三次插值法 (b)SRCNN方法

(c) FSRCNN方法 (d) ESPCN方法

(e) 本文方法 (f) 原始图像图4 测试图像1

(a) 双三次插值法 (b) SRCNN方法

(e) 本文方法 (f) 原始图像图5 测试图像2

本实验评价采用主观评价和客观评价共同分析生成图像质量。其中主观评价就是在图像的视觉效果上感受图像的效果，对比各种方法生成的图像之间的差异；客观评价以峰值信噪比PSNR和结构相似性SSIM来进行衡量。

(1) 峰值信噪比。峰值信噪比是重建的高分辨率图像真实高分辨率图像之间的像素差值的量度，可以用来衡量被处理后图像的质量，单位为dB。定义如下：

(5)

(6)

式中：I为真实图像，K为生成图像，m和n分别为图像和长和宽。

(2) 结构相似性。结构相似性为两幅图像结构相似度的度量的标准，取值范围为[0,1]，值越大就越表示两幅图像结构相似程度越高。定义如下：

(7)

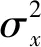
表1和表2分别列出了4组测试图像的生成图像和原始图像进行计算的PSNR和SSIM的值。

表1 图像重建结果的PSNR

表2 图像重建结果的SSIM

3.2 实验结果分析

从图4和图5的实验结果可以看出，使用本文方法生成的图像略优于其他方法。如图4的花瓣的边缘，图4(a)和(b)不够锐利清晰，(c)和(d)也比较模糊，且花瓣层次不明显，有一些波纹，(e)花瓣边缘则较为清晰，花瓣层次也比较明显，整体观感会比较舒适。图5的建筑外墙，图5(a)、(b)和(c)的外墙窗户十分模糊，窗户的边缘线条不清晰，(d)的外墙观感稍可，但是整体观感还是比较模糊，(e)的观感最为舒适纯净，外墙窗户边缘较为清晰，细节较为丰富处理效果更胜一筹。其中SRCNN、FSRCNN和ESPCN三种方法和本文方法使用了相同的训练集和训练次数，在同样的训练条件下，本文的优化方法是有一定的优化效果的。这在表1和表2中的数据也能得到证明，在计算出的PSNR和SSIM值中，可以看出使用本文方法在客观评价方面，较其他的方法高出不少。

4 结 语

本文提出一种改进的基于卷积神经网络的图像超分辨率方法。主要在经典的SRCNN方法的基础上进行了改进，即加深了网络层并且引入残差网络避免退化问题，而且将上采样过程改为在网络内部进行。这样可以加强网络能力并且减轻计算量，最终得到效果更好的图像，而且训练次数要求更低。实验结果表明，本文方法从主观和客观角度，生成图像均好于双三次插值法和SRCNN方法，证明本文提出的改进是有效的。