非理想条件下极化滤波器的干扰抑制性能建模与分析

戴幻尧，陈 卓，王建路，刘文钊

(1.电子信息系统复杂电磁环境效应国家重点实验室，河南 洛阳 471003；2.武警北京市总队，北京 100000；3.中国洛阳电子装备试验中心，河南 洛阳 471003)

0 引言

近年来，随着雷达极化理论研究的逐步深入和雷达器件水平的大幅度提高，极化滤波在抗干扰技术领域中日益占据了愈来愈重要的地位[1-5]。学者针对不同的用途设计了多种极化滤波器，包括单凹口极化滤波器(SPC)、多凹口极化滤波(MLP)、自适应极化滤波(APC)、频域极化滤波器、干扰抑制极化滤波器(ISPF)、最优极化滤波器(OPC)、极化白化滤波器(MPWF)、SINR极化滤波器等[6-15]。在干扰与目标的回波极化不同的情况下，极化滤波可以有效地抑制干扰，对不同入射波在极化域的选择性改善了信号的接收质量。然而，纵观过往的研究，大都假设干扰方向在主瓣方向，忽略了天线极化特性的影响，往往没有考虑通道幅相误差、通道噪声以及极化测量算法对极化滤波器性能的影响。直观地认为，极化滤波的效能仅取决于极化估计精度[16-17]。对极化滤波器评估时，仅从真实极化和估计极化间的差异进行理论分析，忽视了极化滤波的对象并非真实极化，而是接收极化。具体而言，接收通道的输出信号直接表征了在天线极化特性、方向特性、通道幅相特性、噪声特性以及极化处理算法等因素共同作用影响下电磁波信号的幅度和相位特性。正交极化双通道输出信号可直接作为入射波极化的估计，即是对当前条件下电磁波极化的最优估计，对应着极化估计算法的稳态解。但是，此时极化通道的输出并不能作为真实极化的无偏估计，即根据通道输出信号所测量的极化信息蕴含了一定的极化误差，极化滤波矢量也是根据该极化误差建立的。因此，这种误差在极化滤波时被补偿了，即因通道不一致、天线极化特性等因素产生的极化误差不会影响极化滤波的有效性，极化估计的精度不能直接制约极化滤波性能的好坏。从极化滤波的系统角度出发，本文证明了上述结论，给出了较为详细的数学分析，这对于改进现有单极化雷达、增强其极化测量和抗干扰能力具有重要意义。

1 基于正交极化通道的极化估计

eJ(t)=hJJ(t)

(1)

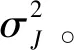
设极化天线的主极化归一化方向图为gH(θ)，交叉极化归一化方向图为gV(θ)，天线峰值增益为Gr，则天线空域极化矢量记作：

(2)

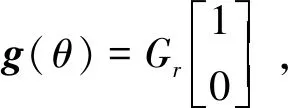
设Γ为正交极化双通道幅相不一致性系数矩阵，Γ=diag[rH,rV]。rH=AHejφH，rV=AVejφV分别为水平垂直极化通道的幅度误差和相位误差。

因此，干扰信号进入水平极化通道的实际接收电压为：

(3)

同理，垂直极化通道的实际接收电压为：

(4)

根据式(3)、式(4)可知，正交极化通道对干扰信号接收的同时，调制了接收通道特性、射频链路特性、天线空域极化特性，以及干扰的幅相特性，接收通道接收机噪声电平。因此，为分析极化测量误差的性能，可以从上述因素出发，并综合考虑极化测量算法，找到制约极化测量精度的因素，给出比较详细的评估。

1.1 天线极化特性的影响

大多数研究极化滤波或目标极化鉴别的文献中想定的前提一样[4-16]，均假定干扰机和极化测量雷达位于对方天线的电轴方向上。实际上，在真实的雷达攻防对抗中，干扰机自身的姿态变化和雷达波束指向偏离阵面法向工作时，攻防对抗的双方通常会偏离对方的电轴方向，因此，原有文献中的假设并不合理。特别是对于机械扫描雷达来说，从旁瓣实施干扰的掩护式干扰机施放的干扰信号总位于偏离电轴的方向。

在非电轴方向上，互为极化正交的天线接收到的电磁波不仅受到天线增益的调制，还会受到天线空域极化特性矢量的调制，不再保持严格正交，而是保持一定的相关性。在这种情况下，干扰机生成的干扰信号与电轴入射时具有不同的特性，极化估计和极化滤波的性能需要严格的分析和证明。

当干扰信号位于雷达天线的主瓣内时，式(3)、式(4)可写为：

(5)

(6)

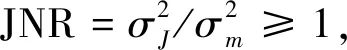
(7)

若通道之间不存在幅相位误差，那么式(7)进一步写为：

〈VV(t)/VH(t)〉=hJV/hJH

(8)

ρJ=〈VV(t)/VH(t)〉=hJV/hJH=tanγJejφJ

(9)

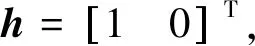
γH(θ)=KPolar|θ|，θ∈[-θ0/2,+θ0/2]

(10)

γV(θ)=2-1π-KPolar|θ|，θ∈[-θ0/2,+θ0/2]

(11)

式中，KPolar>0是天线极化角的变化率，KPolar越大，说明天线的极化变化越快，也可以说是天线的空域极化特性越明显，且极化角φH(θ)=-φV(θ)。

当干扰信号位于雷达天线的旁瓣附近时，式(3)可写为：

VH(t)=rHPSkRFGrLR-1(cos(γ(θ))hJH+

sin(γ(θ))hJVexp(jφH))J(t)+nH(t)=

rHPSkRFGrLR-1(cos(KPolar|θ|)hJH+

sin(KPolar|θ|)hJVexp(jφH(θ)))+nH(t)

(12)

同理，

VV(t)=rVPSkRFGrLR-1(cos(2-1π-KPolar|θ|)hJH+

sin(2-1π-KPolar|θ|)hJVexp(jφV(θ)))=

rVPSkRFGrLR-1(sin(KPolar|θ|)hJH+

cos(KPolar|θ|)hJVexp(jφV(θ)))+nV(t)

(13)

根据天线理论可知，任意一个观测位置下主、交叉极化矢量在球坐标系下是相互正交的。那么，任意两次观测时天线的极化构成了极化空间的一组完备基。

那么在干扰所占据的单元处，正交极化通道输出信号之比近似为：

〈VV(t)/VH(t)〉≈(rVPSkRFGrLR-1(sin(KPolar·

|θ|)hJH+cos(KPolar|θ|)hJVexp(jφV(θ)))/

[rHPSkRFGrLR-1(cos(KPolar|θ|)hJH+sin(KPolar·

|θ|)hJVexp(jφH(θ)))]=[sin(KPolar|θ|)hJH+

cos(KPolar|θ|)hJVexp(jφV(θ))/(cos(KPolar|θ|)hJH+

sin(KPolar|θ|)hJVexp(jφH(θ)))=(tan(KPolar·

|θ|)hJH+hJVexp(jφV(θ)))/(hJH+tan(KPolar·

|θ|)hJVexp(jφH(θ)))

(14)

将干扰信号的极化写成极化比的形式，对于任意固定的θ，tan(KPolar|θ|)=mp，则式(14)可写为：

〈VV(t)/VH(t)〉=(tan(KPolar|θ|)+ρJexp(jφV(θ)))/

1+tan(KPolar|θ|)ρJexp(jφH(θ))=

(mp+ρJexp(jφV(θ)))/(1+mpρJexp(jφH(θ)))

(15)

由式(15)可以看出，此时由极化通道输出的估计极化关于真实极化呈现非线性变化，主要受到两个因素的影响，其一是干扰入射方向上天线的极化角，其二是干扰入射方向上天线的相位特性。这说明从副瓣进入的干扰信号，经过两个极化通道接收功率较主瓣进入有所下降，并且输出信号的极化受到了天线极化特性的调制，极化特性有所变化，极化幅度和相位均产生估计误差，即通过正交极化通道输出直接估计的极化显然不能视为干扰极化的无偏估计。极化估计误差随天线特性和输出电压的变化规律如图1所示。

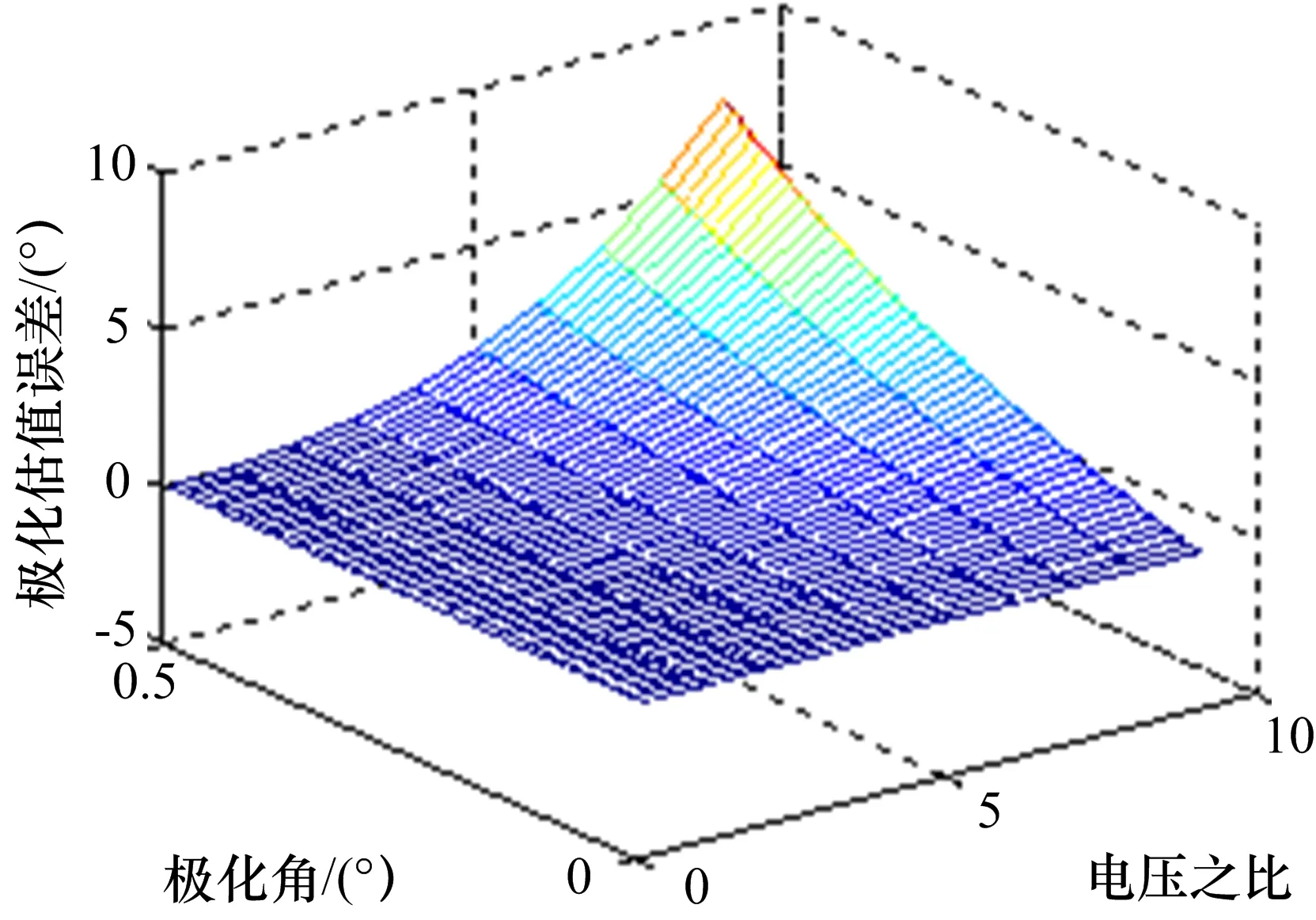
图1 极化估计误差随天线特性和输出电压的变化规律

1.2 极化通道特性的影响

在理想条件下为简化分析，阵元响应、阵元位置扰动、互耦、信号波前畸变往往都被省略，但实际系统中，上述因素的存在都是不可避免的，会对接收信号产生较大影响，这些误差可以综合用“幅相误差”来表示。虽然在工程实现中会对幅相误差进行校正，但剩余幅相误差仍然存在。因此，研究幅相误差对极化估计和极化滤波性能的影响是在实际应用中首先要考虑的问题。

在幅相误差的影响下，水平极化通道对干扰信号的实际接收电压为：

(16)

垂直极化通道对干扰信号的实际接收电压为：

(17)

因此，正交极化通道输出信号之比近似为：

〈VV(t)/VH(t)〉=(AVejφVPSkRFGrLR-1hJVJ(t)+

nV(t))/(AHejφHPSkRFGrLR-1hJHJ(t)+nH(t))≈

(AVejφV/AHejφH)(hJV/hJH)=ξAexp(jφξ)(hJV/hJH)

(18)

式中，ξA=AV/AH为通道间幅度不一致误差，φξ=φV-φH为通道间相位不一致性误差。

因此，极化通道输出的信号的极化给信号真实极化特性调制了一个幅度误差项和一个相位误差项。

1.3 接收机噪声的影响

选择水平、垂直线极化(h,v)为极化基，干扰入射波的电场矢量在(h,v)上为h=[jhjv]T，通过正交极化双通道测量系统接收后，通道输出构成一个二维复矢量，记为x=h+n，其中n为测量系统的噪声矢量，若不考虑杂波和干扰，n通常表示两路通道接收机的输出噪声。实际情况中通常以测量系统的输出矢量直接作为入射信号极化的估计[16]，即有：

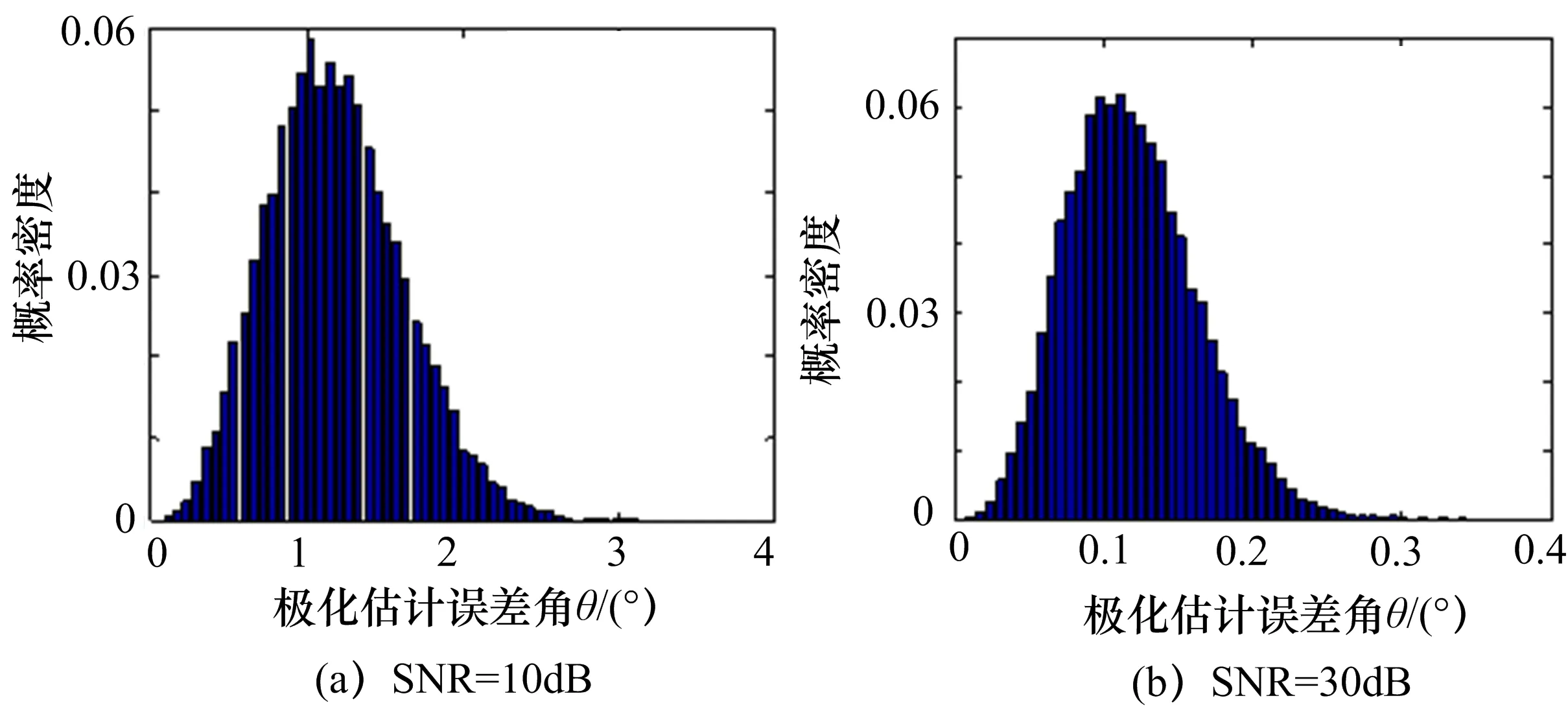
图2 极化估计误差角θ的概率密度分布

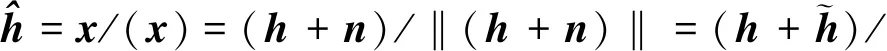
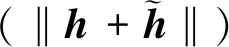
(19)

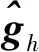
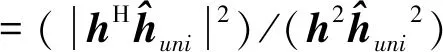
(20)

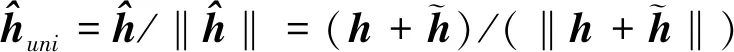
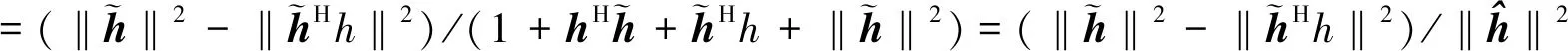
(21)

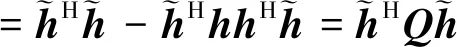
(22)

式中，Q=I2×2-hhH，I2×2=diag{1,1}，易知Q必为非负定Hermite矩阵。

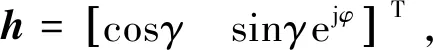
ϑ≈2(bHΛb)1/2

(23)

1.4 极化测量算法的影响

实际雷达中，通常以测量系统的输出在时域内用统计特性来描述干扰的极化状态，但是根据极化状态的时频不变性，信号的极化也可以在频域内完成。为了比较在两种处理域内极化测量的精度，下面给出极化信号频域测量的数学原理和测量性能比较。

根据信号极化的stokes参数，时域的极化参数[2]可以通过式(24)获得:

(24)

(25)

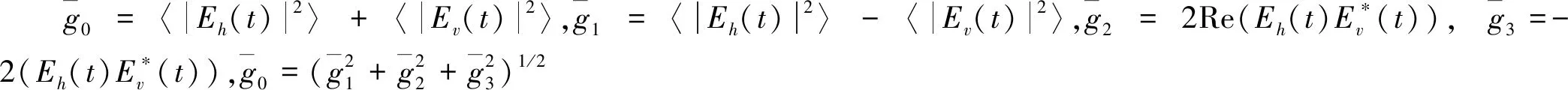
同样,沿z轴传播的平面谐振单色电磁波电场矢量的时间表示形式[15]为：

(26)

式中，Ω为信号角频率，E(t)表示随时间变化的电场强度。

对于振幅不变、极化恒定的单频信号，略去绝对相位，其时间函数可按式(27)表达：

EH(t)=Eh(t)ejΩt

EV(t)=Ev(t)ej(Ωt+η)

(27)

用ρs=Ev(t)/Eh(t)=tgγ表示两极化通道极化比的幅度，η=arg(EV(t))-arg(EH(t))表示两极化通道的相位差。

对两路极化信号进行采样，设采样周期为Ts，对应的数字频率为ω0=ΩTs，采样后数字信号输出：

(28)

式中，N为采样个数，n=1,2,…,N，对这两路信号分别进行FFT，有：

(29)

那么将两路信号频谱的幅度之比作为极化比幅度的估计：

(30)

(31)

因此，通过对两路输出信号进行时域和频域的处理，都可以完成对信号极化状态有效的估计。 图3和图4分别给出了对极化信号进行时域和频域处理提取极化参数的性能曲线，可以很明显地看出，频域的处理方法通过FFT变换相当于对时域进行了相关积累，提高了信噪比(SNR)，估计精度要高于时域处理方法。

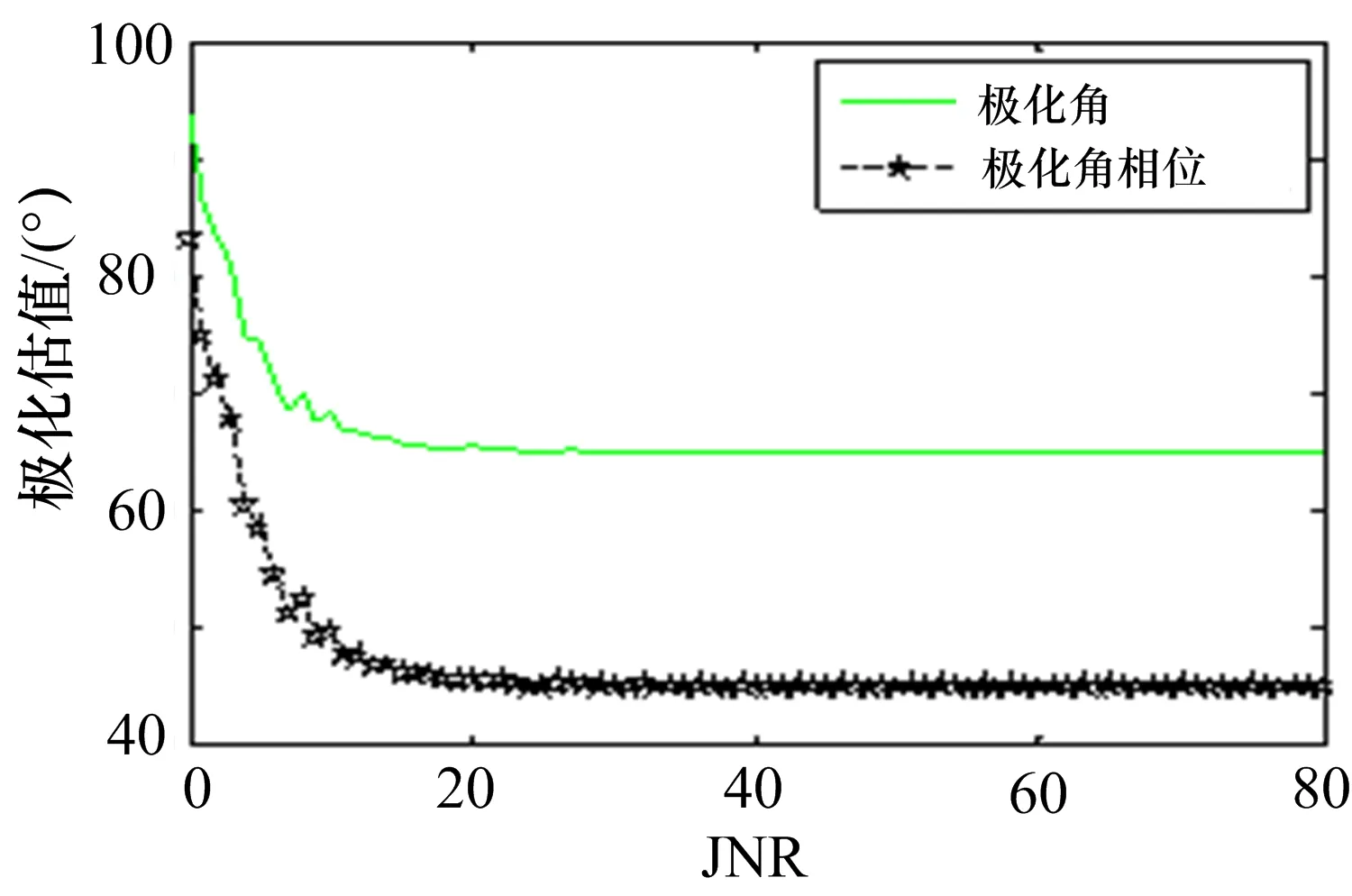
图3 极化状态的时域估计性能

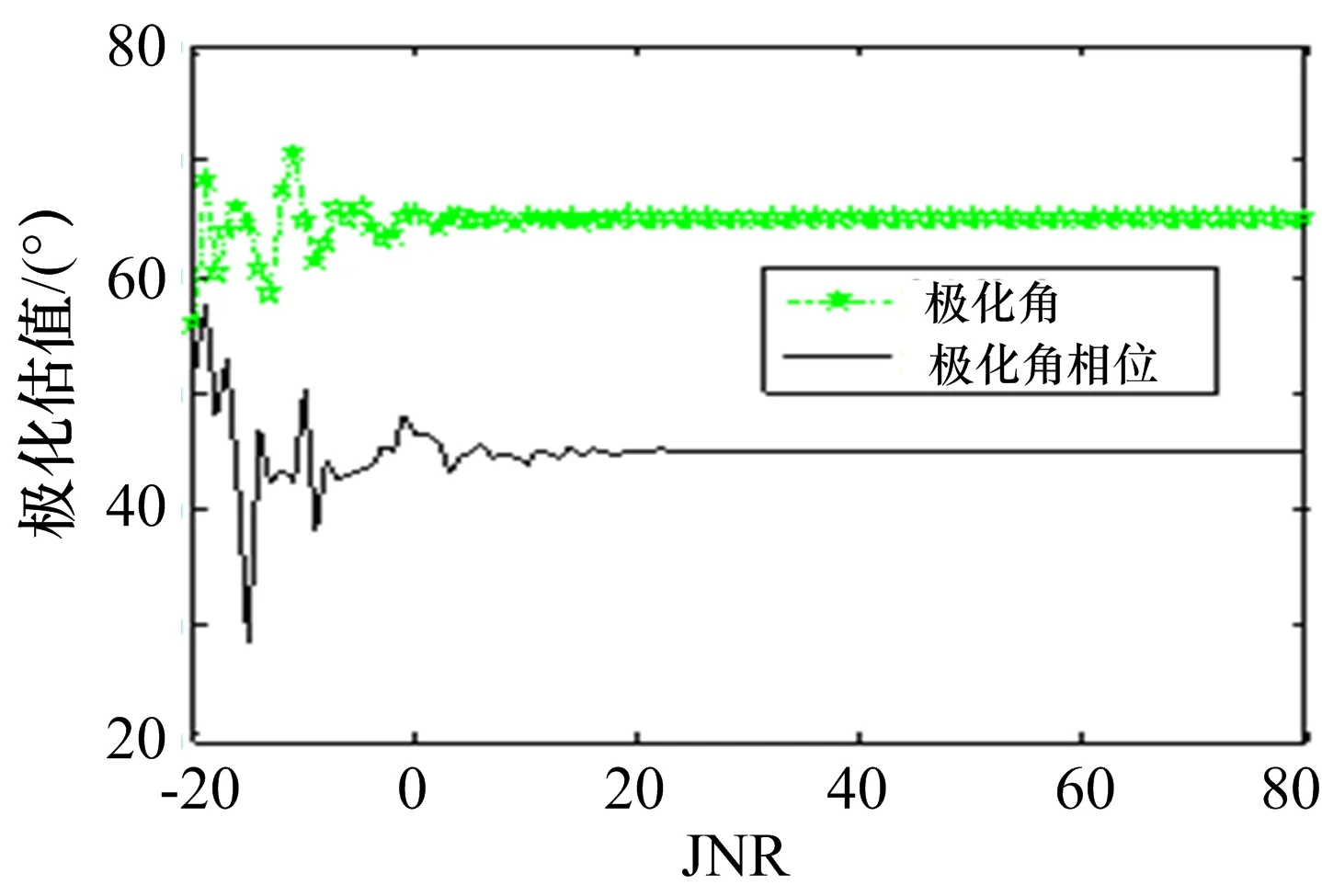
图4 极化状态的频域估计性能

2 极化滤波有效性分析

极化滤波有效性不仅要考虑噪声，综合上面3个因素，传统的分析是错的，即若估计无误差时，剩余功率为0。分析不正确。

(32)

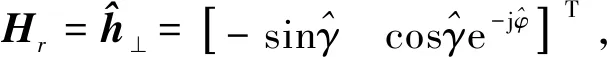
(33)

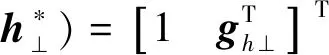
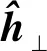
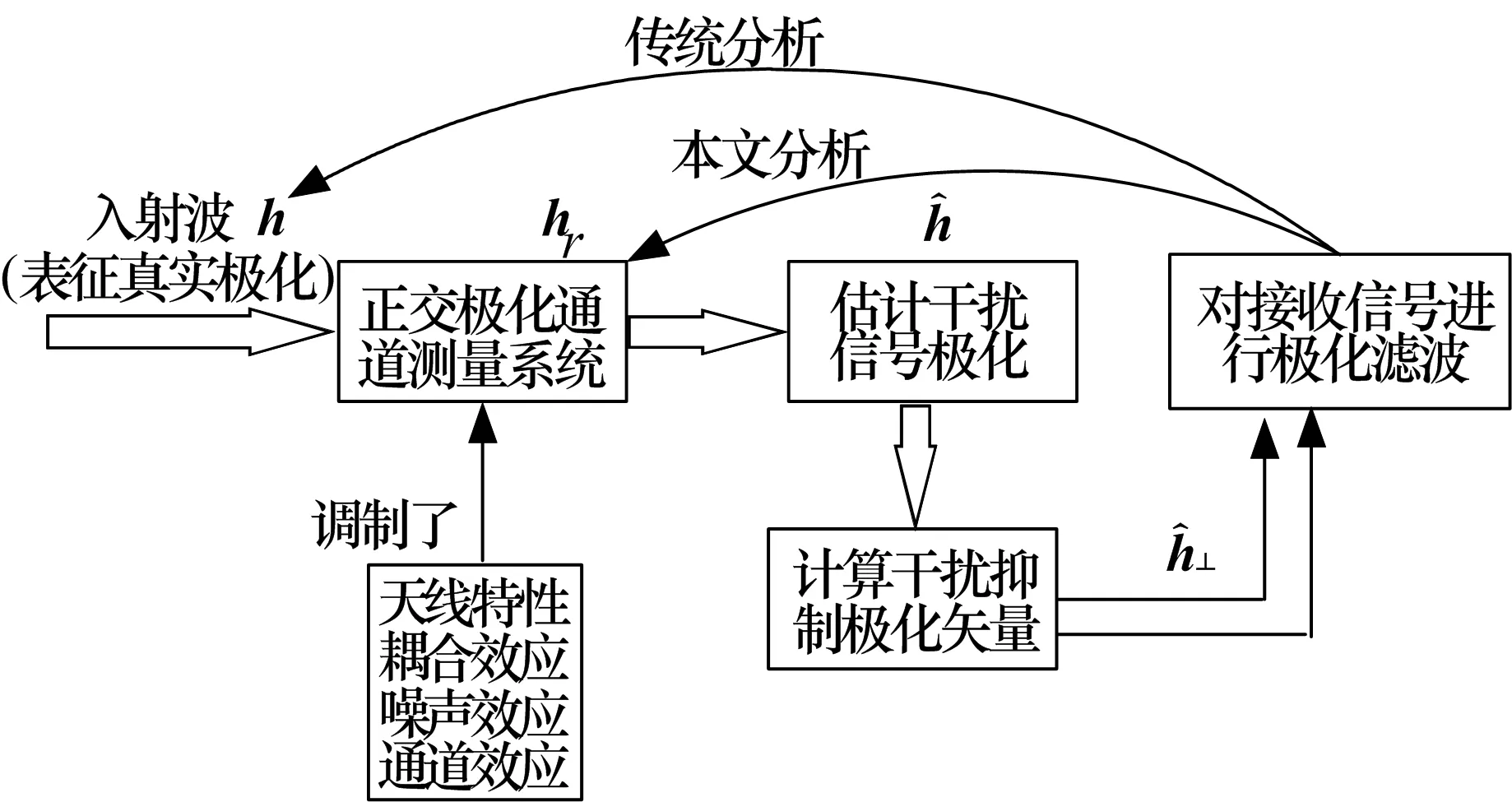
图5 实际极化雷达中极化滤波器的开环模型

对于入射信号而言，由于经过雷达接收天线的空域极化特性的调制，以及单元耦合效应、通道噪声和幅相误差的影响，正交极化通道的输出已不适合作为电磁波极化的最优估计了，更表现为一种近似解。因此在极化滤波性能的传统分析中，通常用带估计误差的极化建立滤波矢量，进而对入射“真实极化”进行滤波是不符合实际信号处理流程的。应该在整个实际极化雷达中极化滤波的开环模型中增加一个“输出极化hr”的环节，通过来波真实极化、输出极化、估计极化这3个量来判断极化滤波的性能，而不是单纯从估计极化和来波真实极化两个方面来建立评估准则。

因此，式(33)可改写为：

(34)

式(34)包含两项，一是根据通道输出得到的估计极化，存在一定的估计误差，对误差的建模和分析在第2节已给出具体分析;二是噪声矢量。单独分析第一项可知滤波后输出信号可表示为：

(35)

易知第一项输出功率近似为0。

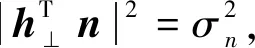
由上面的分析可以看出，极化估计误差环节和极化滤波矢量环节是互相影响的，极化估计误差在极化滤波矢量估计环节被补偿了，极化滤波矢量是建立在极化估计误差上的，因此，在实际处理当中，极化估计误差不会影响极化滤波的有效性。或者系统误差对极化滤波没有影响，即极化通道幅相一致性误差没影响。

3 结束语

极化滤波是雷达极化域抗干扰领域的经典课题。从实现的信号处理结构上看，极化滤波器可用正交极化双通道测量极化估计器、干扰抑制极化计算器、极化滤波接收器这三个环节构成的开环网络来建模。基于这一理论模型，本文从天线极化特性、通道幅相误差、通道噪声效应、极化测量算法四个方面，分析了对极化估计的影响，给出了在极化估值误差条件下极化滤波有效性的证明。本文的研究说明，在评估和验证极化滤波的有效性时，或者在雷达传感器中增加极化滤波环节以实现抗干扰的目的时，优化极化通道的输出和处理才是关键环节，极化估计器的精度并不直接制约整个极化滤波器的滤波效果。这是因为正交极化双通道输出数据以及时频域测量的极化已经包含了极化误差，极化滤波矢量是建立在极化估计误差上的，但是该误差在极化滤波时一并被补偿了，不会影响极化滤波的有效性。该结论对于改进现有单极化雷达、增强其极化测量和抗干扰能力具有重要意义。■