基于正弦模糊数云模型的轨道交通施工风险评价方法

商兆涛，石 峰，夏 琴，卢坤林

(1.芜湖市轨道(隧道)交通工程质量安全监督站，安徽 芜湖241000；2.合肥工业大学 土木与水利工程学院，安徽 合肥230009)

随着轨道交通体系建设的快速发展，轨道交通建设项目不断增加。但轨道交通类的项目施工条件复杂，对项目风险管理能力提出了极大的挑战，故建立一种系统、科学的轨道交通施工风险评价方法成为轨道交通领域的重要课题[1-2]。轨道交通施工过程中风险指标具有不确定性和模糊性，需采用可靠的数学方法对其进行定量分析，学者们通过采用三角模糊数[3]、正态模糊数[4]、梯形模糊数[5]、区间数等方法[6]初步解决了轨道交通施工风险评价过程中的不确定性问题。其中：正态模糊数的分布更接近于人类思维，但计算不方便；对于三角模糊数方法，专家打分区间线形分布，给评价结果带来一定的影响，实际情况专家打分在最可能值附近相对集中；对于梯形模糊数方法，最可能值集中在某区段，而该区段范围很难合理确定。因此需改进有关轨道交通施工风险的评价方法，其中模糊数综合评价模型嵌入云模型的模糊综合评价方法能较好地评价轨道交通施工风险，但仍需进一步改进和提高[7-9]。鉴于此，文中将正弦模糊数综合评价模型嵌入云模型，构建基于正弦模糊数的云模型风险评价方法，该方法应用于芜湖轨道交通施工项目中取得了良好的效果。

1 正弦模糊数综合评价模型

1.1 正弦模糊数模型的建立

传统三角模糊数隶属函数呈线性分布，如图1。其中l1,m1,u1分别为专家打分的最低值、最可能值、最高值，而实际情况中专家打分集中在最可能值附近。由图1 可见，正弦模糊数隶属函数专家打分最可能值附近隶属度相对较高，最低分l1和最高分u1附近值隶属度相对较小，其表示形式更贴合实际。由此看出，三角模糊数的方法与实际情况相差较大，故文中构建正弦模糊数综合评判模型确定指标权重。

根据模糊数的概念[10-12]，对正弦模糊数的相关概念作如下推导。

1)记F(y)为R 上的全体模糊集，称P 为正弦模糊数，正弦模糊数常简记为P=(l,m,u)。如果其隶属函数为Up(x)：R →[0，1]，则

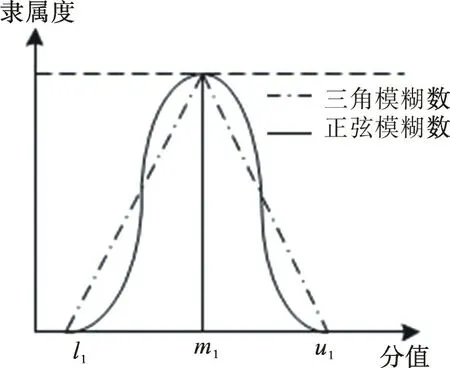
图1 隶属函数对比图Fig.1 Contrast of membership functions

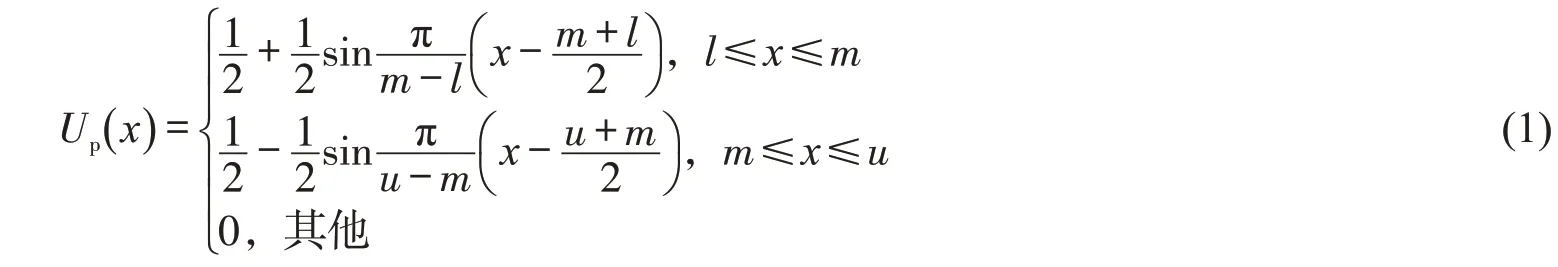
其中，x ∈R。正弦模糊数定义隶属函数的区间数，上、下限分别为l，u，且l ≤m ≤u，l 和u 对应最小隶属度0，m 对应最大隶属度l，且u-l 越大，其模糊程度越强。

2)每个正弦模糊数对应一个非模糊数，设P=(l,m,u)是正弦模糊数，根据几何方法确定其对应的非模糊数，即S=(l+2 m+u)/4。

设正弦模糊数P=(l,m,u)，其α 截集Pα=[l(α),m(α),u(α)],0 ≤α ≤1)，为了求出α-级区间，在(1)式中令xl=l(α),l ≤x ≤m 和xu=u(α),m ≤x ≤u，即得

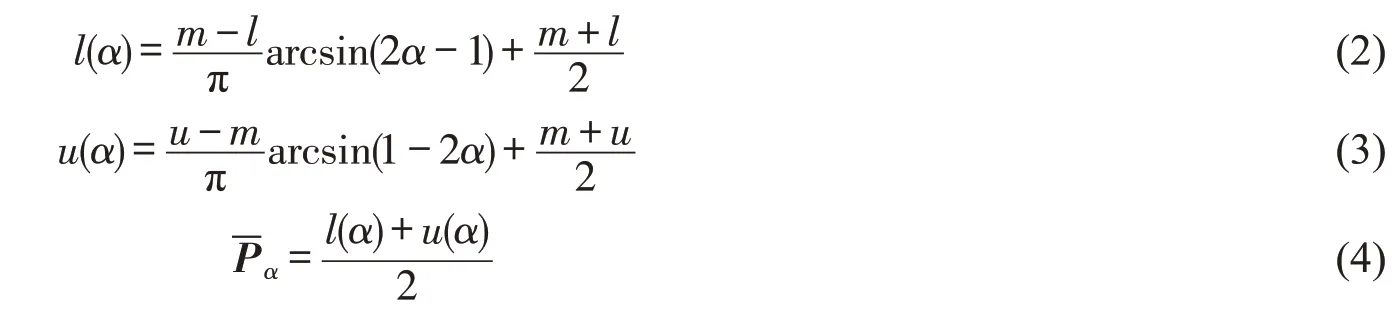
其中-Pα为Pα的平均值，即[l(α),u(α)]的中点，可求出正弦模糊数P 的均值面积：

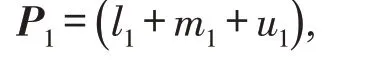
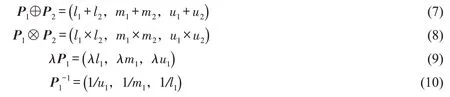
4)图2中横坐标d 的纵坐标D 在0和1之间，根据D 的纵坐标给出P1＞P2的可能性程度为：

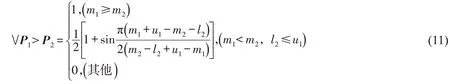
1.2 风险指标的确定

正弦模糊数指标权重的确定可分为以下几步。

1)根据层次分析法的原理收集资料，确定问题的总目标，建立问题的目标层、一级指标、二级指标，将同一层次的因素进行比较和评价。

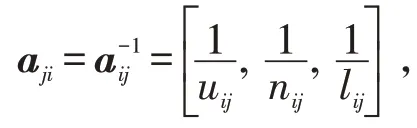
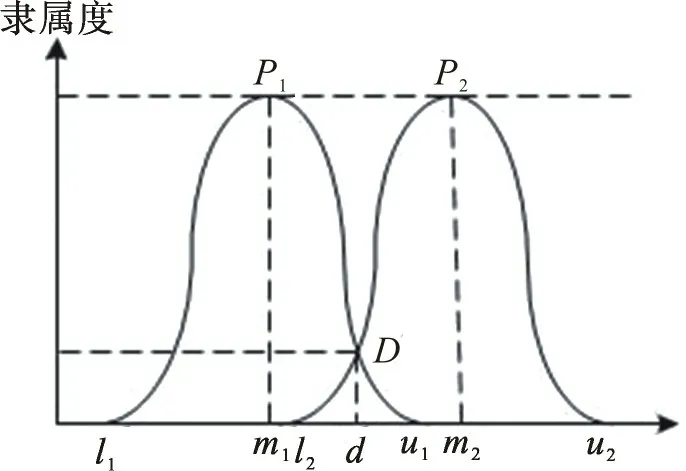
图2 P1＞P2 的可能性程度Fig.2 Possibility of P1＞P2

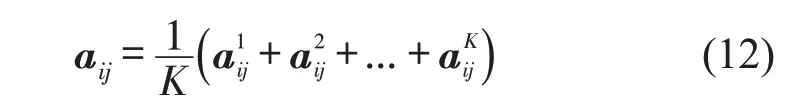
层次分析法的1～9 标度法如表1，正弦模糊数的取值可根据此方法确定，下界l 和上界u 可表示出模糊程度。

3) 利用公式CI=(Imax-n)/(n-1)进行一致性检验，其中CI为综合一致性指标，Imax为正弦模糊数中间数mij构成新矩阵A 的最大特征根；再利用公式CR=CI/RI得出一致性比率，其中RI为随机一致性指标，取值如表2。满足CR＜0.10 时，则认为判断矩阵A 满足一致性条件；如果不满足此条件，则需专家重新打分，直到判断矩阵满足条件即可[13]。

表1 风险因素标度法Tab.1 Scaling method of risk factor

表2 RI的取值Tab.2 Value of RI

4)计算模糊判断矩阵中各指标的综合重要程度Si，如公式

5)利用正弦模糊数原理计算层次单排序第i 个指标Bi重要于其他指标的可能性程度，通过比较确定正弦模糊数的大小，如公式

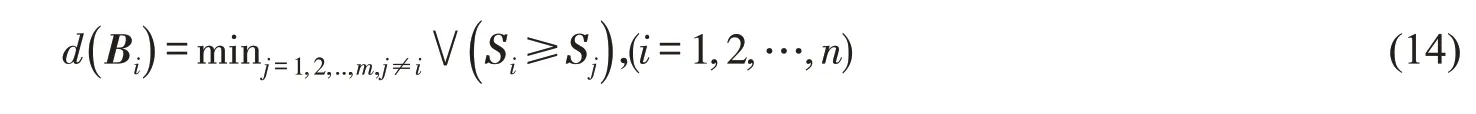
6)层次总排序。通过计算得出每一个层次的指标，然后将每一个层次进行单排序，求出每一层次指标权重W，并经过归一化处理，即可得到相应的指标权重。最后通过比较同一层次所有指标与最高层的重要性即可得到层次总排序。指标权重越大，对轨道交通施工风险的重要程度越大。

1.3 风险等级的确定

1.3.1 正态云及生成算法

逆向云生成算法是将云滴样本转化为云数字，也就是将精确数进行定性的表达，云的数字特征反映定性知识的定量特性，用期望值E、嫡E′、超嫡H 等3个量来表示。为使计算便捷，文中采取无需确定度信息的逆向云算法，其计算方法如下：

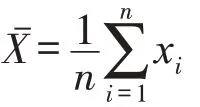
2)E=Xˉ；

通过以上计算，可得到样本数据的云数字特征(E,E′,H)，云与精确数值的算法可表示为：

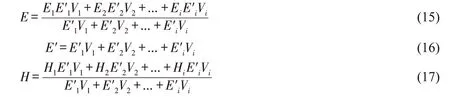
其中：E，E′，H 均为第n-1 层指标的评价云模型；Ei表示第n 层指标评价云模型的期望值；E′i表示第n 层指标评价云模型的熵；Hi表示第n 层指标评价云模型的超熵；i 为第n 层指标的个数；Vi表示第n 层指标的权重。因此，采用式(15)～(17)计算出目标层的综合评价云模型。

1.3.2 云模型的评价

收集专家评语集。由于专家评语表现模糊，如“低风险”“中度风险”和“高风险”等表述，因此采取一维云模型的方式构建指标体系的评价标准云模型集。若指标评语存在双边约束(Cmin,Cmax)，如“较低风险”，可通过下式求出云模型的数字特征：

式中k为常数，表示评语本身的模糊程度，由专家经验给出。

2 应用实例

2.1 工程概况

芜湖轨道交通1 号线保顺路站至华山路站区间如图3。保顺路站至华山路站区间起讫里程总长为1 245.4 m，从保顺路车站到华山路车站出站后顺着和平路沿路中行走，全段均为高架区间，高空作业较多，本区间附近有地表水，地下水影响较小。本区间主要影响因素是47 个墩位(不含车站)。其中：受电力线影响(包括高压电线和地下电缆)6个；受弱电影响6个；受污水管影响39个；受燃气管道影响2个；受扁担河桥影响2个。

2.2 施工风险评价指标体系

根据芜湖轨道交通1号线保顺路站至华山路站区间的施工条件与特点构建风险评价指标体系，该指标体系分为5个一级指标和19个二级指标，如图3。

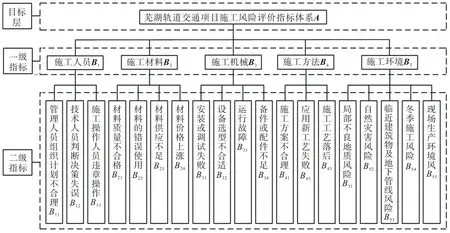
图3 芜湖轨道交通1号线保顺路站至华山路站区间施工风险评价指标体系Fig.3 Construction risk evaluation index system from Baoshun Road Station to Huashan Road Station of Wuhu Rail Transit Line 1

2.3 指标权重的确定

建立正弦模糊数模型来确定芜湖轨道交通1号线保顺路站至华山路站区间施工风险指标的权重。首先根据构建的芜湖轨道交通项目施工风险评价指标体系设计芜湖轨道交通项目施工风险评价问卷调查表，主要采用标度法度量调查问卷中选用的指标，问卷调查采用电子邮件的形式发放，待专家评价后回收。根据芜湖轨道交通项目施工风险评价调查问卷表，构造目标层A的判断矩阵，如表3。

表3 判断矩阵A-BiTab.3 Judgment matrix A-Bi

1)构造判断矩阵A，如式(19)

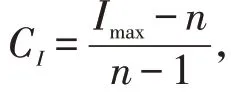
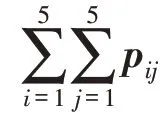
4)根据式(11)进行层次单排序。

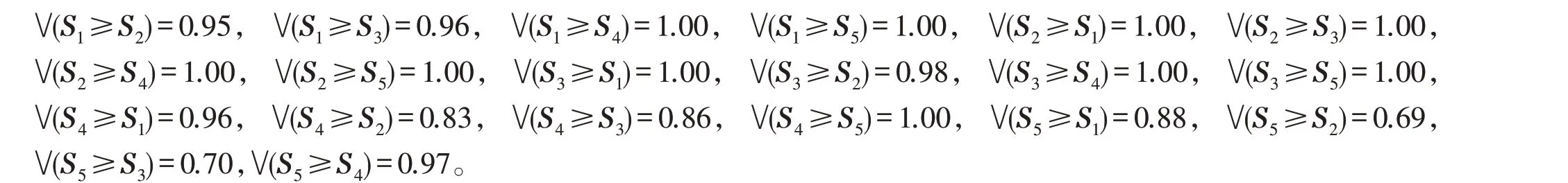
由式(14)计算出各指标重要于其他指标的可能性程度：d(B1)=0.95，d(B5)=0.69。于是，W1=(0.95，1.00，0.98，0.83，0.69)，经过归一化得到准则层相对于目标层的权重向量W=(0.22，0.23，0.21，0.19，0.15)。用正弦模糊数构造一级指标判断矩阵以及权重，如表4。

表4 判断矩阵A-Bi及Bi的权重Tab.4 Judgment matrix A-Bi and Bi weights

采取同样的方法，用正弦模糊数构造二级指标的判断矩阵，并进行层次单排序，其二级指标权重如下：

施工人员B1=(B11，B12，B13)=(0.44，0.37，0.19)；施工材料B2=(B21，B22，B23，B24)=(0.33，0.34，0.32，0.01)；施工机械B3=(B31，B32，B33，B34)=(0.04，0.43，0.38，0.15)；施工方法B4=(B41，B42，B43)=(0.39，0.35，0.26)；施工环境B5=(B51，B52，B53，B54，B55)=(0.32，0.31，0.23，0.07，0.07)。

5)层次总排序。前述为层次单排序，为得到同一层次所有元素相对于最高层的重要性，还须在层次单排序的基础上进行层次总排序。指标层相对于目标层的各权重向量如表5。根据表5可知：在一级指标中，施工材料在芜湖轨道交通1 号线保顺路站至华山路站区间施工风险中所占权重为0.23，重要程度最高，应重点控制施工材料的安全因素；其次，施工人员和施工机械在轨道交通施工风险中所占权重分别为0.22 和0.21，对轨道交通施工同样有重要影响，也应重点防护，确保轨道交通建设顺利进行；对于二级指标，风险因素前两位的分别是B11,B32，即管理人员组织计划不合理和设备选型不合适,其中管理人员组织计划不合理属于一级指标施工人员因素，设备选型不合适属于一级指标施工机械因素。

2.4 风险等级的确定

对于本文的芜湖轨道交通项目施工风险，专家调查结果评语等级定级分别为“低风险”[0，1)、“较低风险”[1，5)、“中度风险”[5，10)“较高风险”[10，30)、“高风险”[30，80]。通过式(18)得到评价标准云模型集结果，如表6。

根据专家打分，利用改进的风险矩阵法确定风险等级，然后利用无须确定度信息的逆向云算法计算出反映定性概念的数字特征E，E′，H。通过计算得到二级指标云模型，如表7。

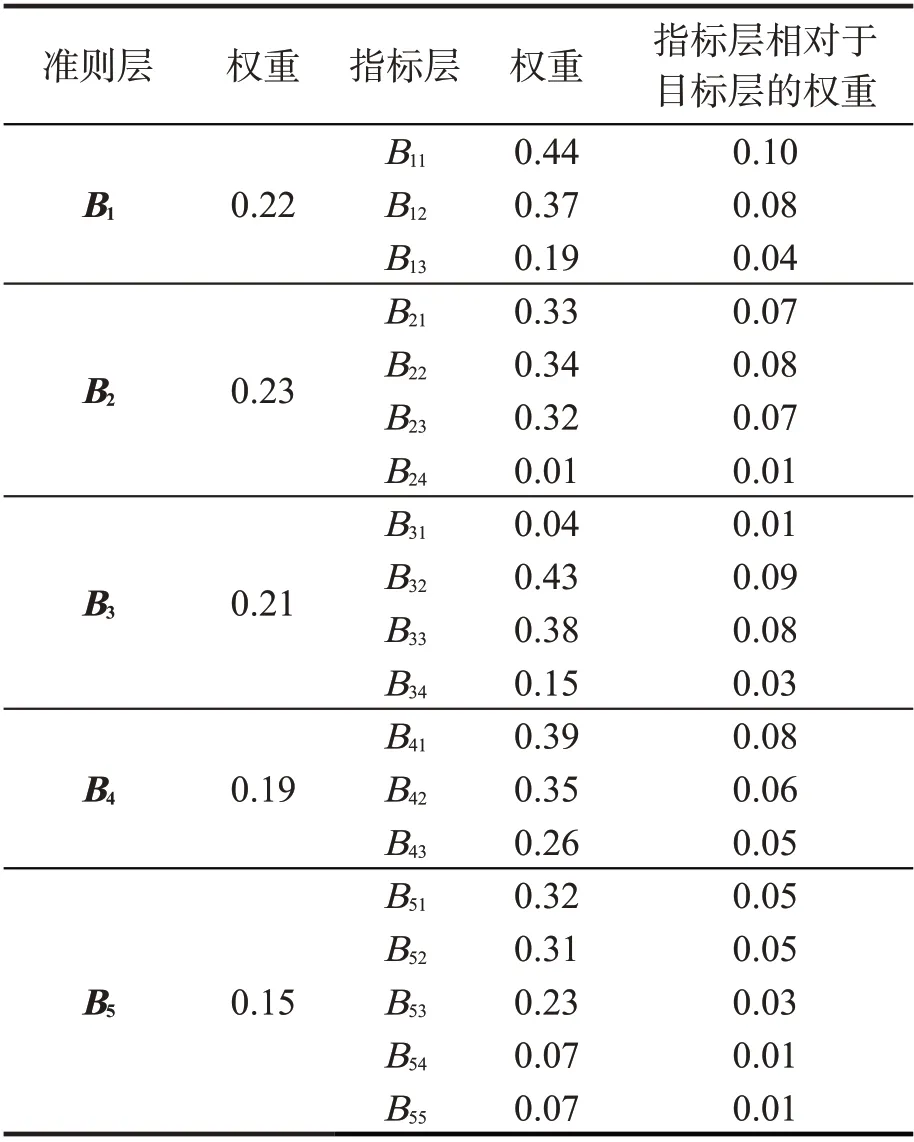
表5 指标层相对于目标层的各权重向量Tab.5 Each weight vector of the indicator layer relative to the target layer

表6 评价标准云模型集Tab.6 Cloud model set of evaluation standard

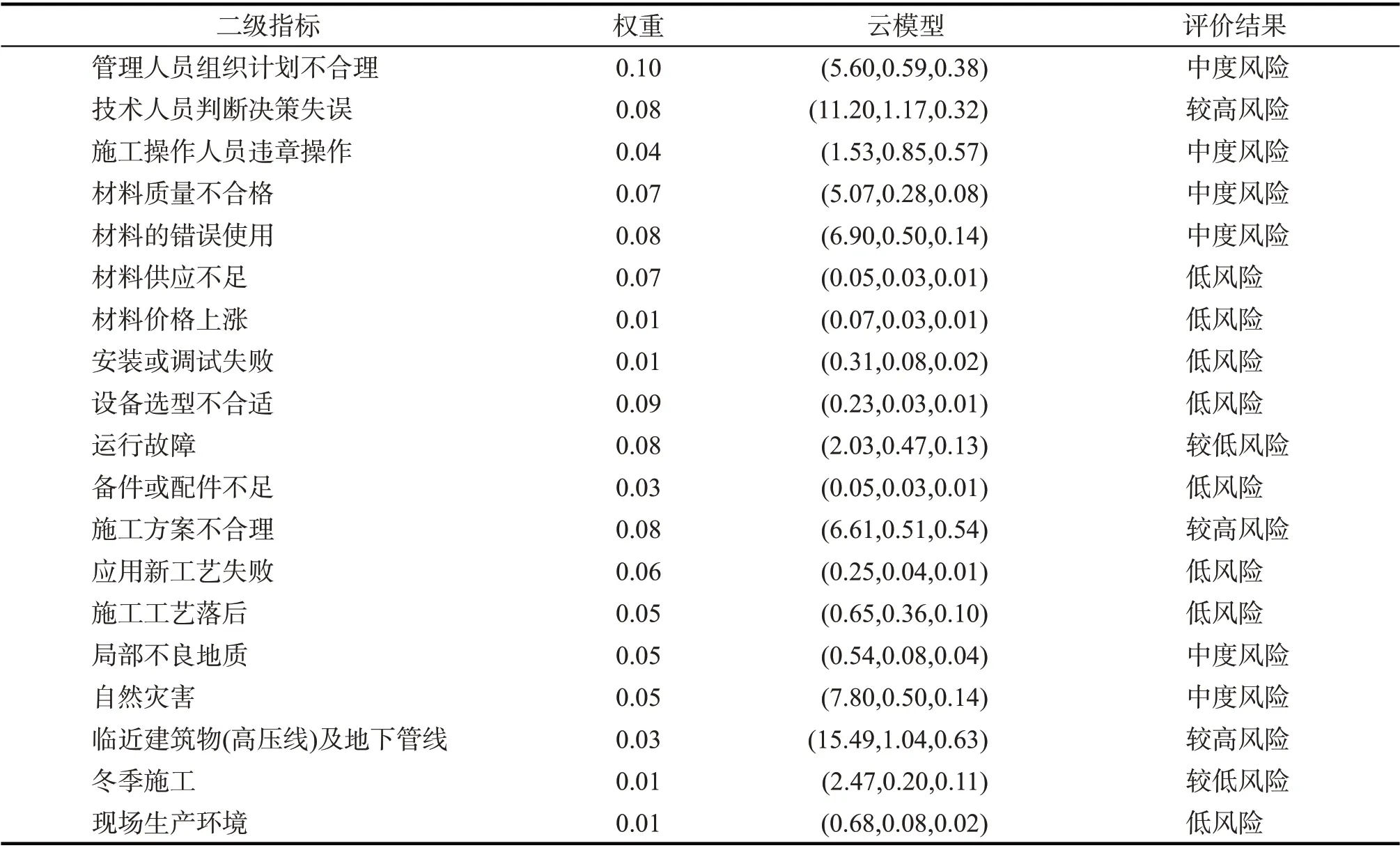
表7 二级指标的云模型Tab.7 Cloud model of secondary indicators

2.5 综合评价云图的确定

根据表7 中二级指标的云模型参数和式(15)～(17)计算出顶层指标的云模型参数：E=6.12，E′=0.41，H=0.32。即顶层指标的云模型参数为(6.12，0.41，0.32)，采用Matlab 得到综合评价云图，如图4。

根据最大隶属原则，确定芜湖轨道交通1号线保顺路站至华山路站区间所处的风险等级，并将综合评价和标准评价进行云图比较。图4 中：①表示低风险；②表示较低风险；④表示中度风险；③表示较低风险和中度风险之间，并且更加靠近中度风险。由图4 可得，芜湖轨道交通1 号线保顺路站至华山路站区间施工风险整体为中度风险。

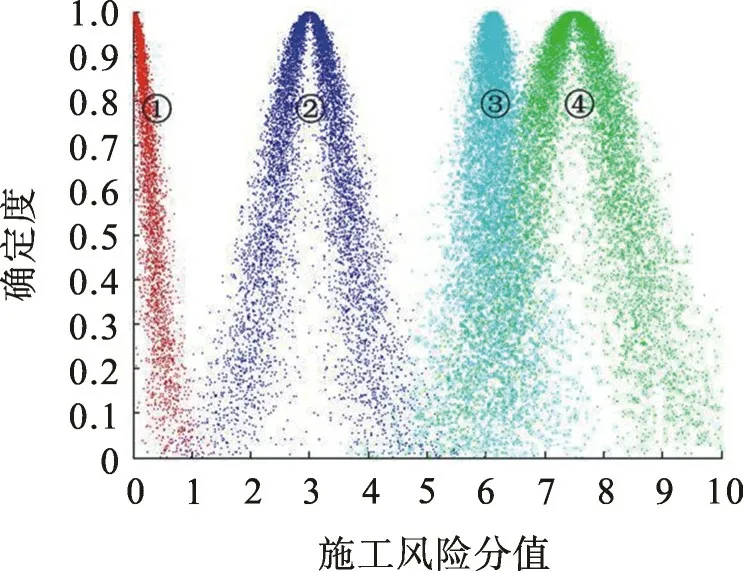
图4 芜湖轨道交通施工风险综合评价云图Fig.4 Cloud chart of comprehensive risk assessment of Wuhu rail transit construction

3 结 论

1)构建基于正弦模糊数的云模型风险评价方法，正弦模糊数隶属函数专家打分最可能值相对集中，实际情况中专家打分集中在最可能值附近，因此其表示形式更贴合实际。

2)采用正弦模糊数模型确定芜湖轨道交通1号线保顺路站至华山路站区间风险指标权重，结果表明：一级指标中，施工材料、施工人员和施工机械重要程度最高，应重点把控；芜湖轨道交通施工风险影响因素较多，二级指标中，应重点把控管理人员组织计划不合理、设备选型不合适等风险因素。

3)采用基于正弦模糊数的云模型风险评价方法确定芜湖轨道交通1号线保顺路站至华山路站区间所处的风险等级为中度风险，云模型能够对施工中风险因素的模糊性进行定性和定量之间的变换。将云模型应用于城市轨道交通项目施工风险评价中，拓展了云模型应用的领域。