基于主成分分析的煤元素分析通用预测模型研究

季玉洁，李 祥，刘翠茹

1.国电科学技术研究院有限公司； 2.国电南京煤炭质量监督检验有限公司，江苏 南京 210031)

煤的热值、工业分析与元素分析数据间有着密切的关系，只要用热值和工业分析数据将这种关系定量表示出来，则煤中各元素含量完全可以由热值和工业分析结果从理论上进行近似计算[1]。经验法、回归分析法和算法等[1-6]已经提出了煤的热值与工业分析及元素分析数据之间较精准的预测模型。但这些预测模型往往未能全面系统地考虑煤的热值和工业分析数据间的交互作用和综合关联关系，特别是通过线性回归法直接获得预测模型时，这种交互作用和综合关联关系的损失尤为明显。而主成分分析法可将原始变量重新组合成一组新的互相无关的综合变量，同时根据实际需要，从中取出几个综合变量，尽可能多地反映原始变量的信息[7]。

鉴于此，本文拟以主成分分析法对煤的发热量和工业分析数据进行预处理，在不损失原始变量信息的情况下对变量进行压缩，获得煤的发热量和工业分析数据的综合作用参数(即主成分)，研究所得主成分与煤的元素分析数据间的关系，进而提出煤元素分析的通用预测模型，并检验模型适应性。

1 煤质数据采集及分析

以2016年4月至2017年10月间国电南京煤炭质量监督检验有限公司所测561个煤样的煤质分析数据(见表1)为研究对象。表2表明研究所用煤质分析数据具有较广的覆盖范围。

表1 煤质分析数据

注：*由“差减法”得到。

表2 煤质分析数据范围

注：*由“差减法”得到。

2 结果与讨论

为提高科学性和严谨性，本文对原始数据进行了以下处理：

(1)对原始数据进行随机重排，重排后结果见表1；

(2)以表1中前500组数据为训练组，后61组数据为检验组；

(3)对训练组数据进行主成分分析；

(4)将检验组数据进行去中心化，进而使训练组和检验组数据转换到同一个坐标系下。其原因是：在进行主成分分析时训练组数据进行了去中心化，即每一个因变量减去其所在列的平均值[8]。

2.1 主成分分析

主成分分析法的基本原理见文献[4-7]。其主要步骤是：

(1)列出指标数据矩阵X；

(2)计算X的协方差矩阵；

(3)计算协方差矩阵的特征值和特征向量；

(4)计算各成分贡献率及累计贡献率；

(5)确定主成分个数和主成分方程。

本文借助MATLAB软件对训练组中煤的工业分析和发热量数据进行主成分分析，结果见表3。

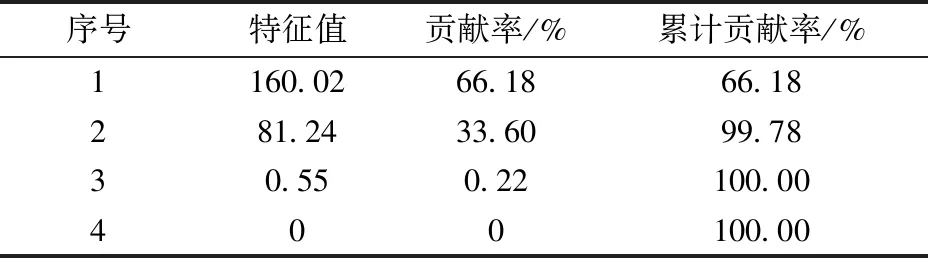
表3 主成分的特征值、贡献率及累计贡献率

根据主成分特征值大于1的原则[9]，确定影响煤的工业分析和发热量数据的主要是前3个主成分，其累计贡献率达100%，已覆盖原始数据的全部信息。前3个主成分记作Z1、Z2和Z3，其得分见表4。由文献[8，10，11]和各主成分的表达式知：第一主成分主要受Ad和Vd的综合影响，其中Ad和Vd分别有较高程度的负载荷和正载荷；第二主成分主要受Vd和FCd的综合影响，其中Vd和FCd分别有较高程度的正载荷和负载荷；第三主成分主要受Qgr，d的影响，其具有较高的负载荷。

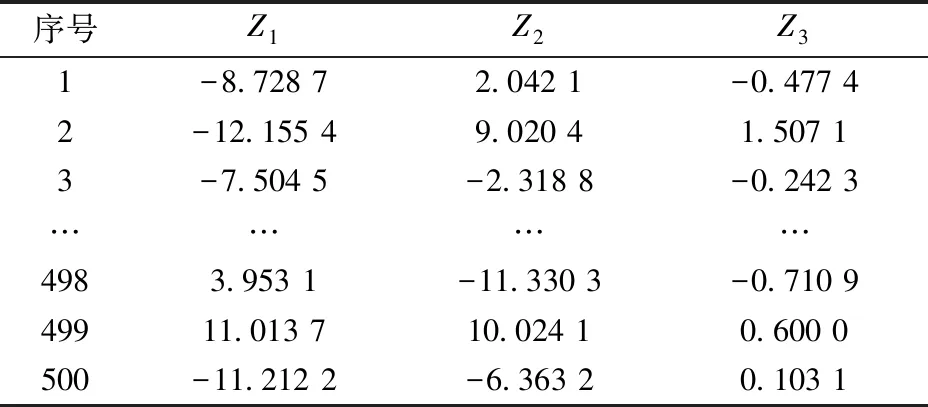
表4 前3个主成分的得分

3个主成分的方程如下：

其中，c为主成分载荷矩阵，

2.2 三元线性回归分析

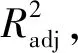
(a)

(b)

(c)

(d)

(e)

(a)～(e)的预测效果见图1。由图1知，3个主成分与煤中各元素的三元线性拟合优度分别为0.997 8、0.937 3、0.972 2、0.207 6和0.247 9。这表明基于主成分—三元线性回归分析的Cd、Hd和Od预测模型具有极好的适应性和有较广的适应范围，其中Cd∈[13.35，79.05]、Hd∈[1.08，5.04]和Od∈[1.28，21.88]。值得注意的是，不同于文献[1，2，13]，本文中Od预测模型的预测精度较高，这表明主成分分析在原始数据处理时起到了关键作用。而基于主成分—三元线性回归分析的Nd和Sd预测模型适应性比较差，其原因是煤中N、S元素含量少、赋存形式复杂，且在煤转化(热解、气化和燃烧等)中析出规律相当复杂[14，15]，与Ad、Vd、FCd和Qgr，d间并非简单的线性关系，即煤中N、S元素与3个主成分间并非简单的线性关系。

2.3 Nd和Sd的BP网络预测模型构建

BP网络是基于BP误差传播算法的多层前馈网络，多层BP网络有输入节点、输出节点和一层或多层隐含节点[16]。通常将一个具有多个输出的网络模型转化为多个具有一个输出的网络模型效果会更好，训练也更方便[17]。鉴于此，本文以主成分Z1-Z3作为输入数据，以Nd和Sd作为输出数据，分别建立基于主成分—BP网络的煤中Nd和Sd的预测模型。

2.3.1 BP网络参数设置

所建BP网络的设计函数为newff，训练函数为train。输入层到隐层的激励函数为S型正切函数tansig，隐含层到输出层的激励函数为对数函数purelin。训练过程的其他参数设置如下：

net.trainParam.epochs = 500；%训练次数设置

net.trainParam.goal = 1e-6；%训练精度设置

net.trainParam.lr = 0.0001；%学习速率设置

net.trainParam.max_fail = 20；% 验证检查设置

理论上，在闭区间内的任何一个连续函数都可以用单隐层的BP网络逼近，因此一个三层的BP网络可以完成任意的n维到m维的映射，而隐含层神经元数目往往需要设计者根据经验和多次实验来确定[18]，大多数学者认为确定隐层最优神经元数最有效的方法是通过反复试验，将能使样本误差达到预设精度的隐含层神经元数目作为网络模型最优的隐含层神经元数目[19]。同时，隐含层神经元数目越多，网络越复杂，泛化能力也就越差，且过多的网络节点会增加训练网络的时间；相反，隐含层神经元数目过少，将使得学习在局部最小中搜索，不能得到可靠的结果[16]。因此，必然存在一个最佳隐含层神经元数。

鉴于此，本文确定BP网络最优隐含层节点数的方法为：

(2)采用试凑法确定BP网络最优隐含层节点数。即从hn=3开始，将输入层、隐含层节点数和输出层相同的BP网络循环运行3 000次，每次运行时，BP网络初始权值和阈值不断变化，保存每次运行产生的BP网络和相应的标准偏差δ；全部运行结束后，获得δ值最小时的BP网络；递增hn，重复上述过程，直到hn=13。

(3)比较hn从3到13过程中的δ值，其中δ值最小时所对应的hn值为最优隐藏节点数(见表5)，即BP net-Nd和BP net-Sd最优hn值分别为6和7。

表5 不同隐含层节点数所对应BP网络的最小标准偏差

2.3.2 基于BP网络的Nd和Sd预测模型适应性分析

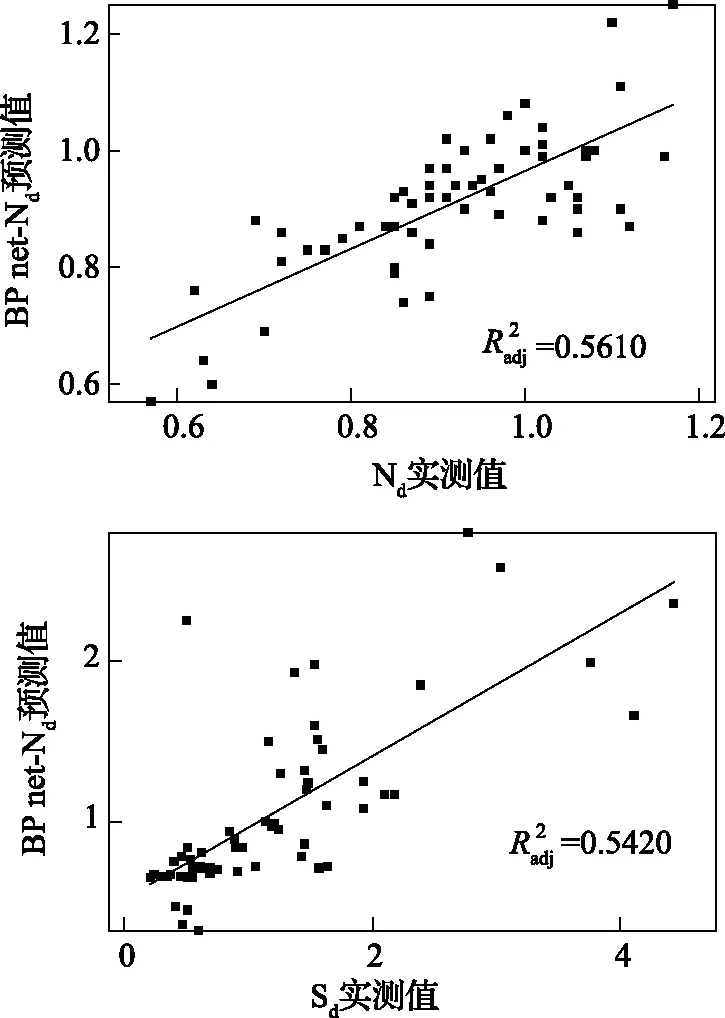
图2 基于主成分—BP网络的Nd和Sd预测模型结果比较

将检验组数据进行主成分变换后，直接加载训练好的最优BP网络，获得相应的Nd和Sd预测值。由图2知，预测值和实验值间的线性拟合优度分别为0.561 0和0.542 0。比较图1和图2，基于主成分-BP网络的Nd和Sd预测模型的适应性较基于主成分-三元线性回归分析时有大幅提升。然而由于煤中N和S元素含量少、赋存形式过于复杂，即便是具有高度非线性泛化能力的BP网络，也未能精准预测煤中N、S元素含量。在预测精度允许的情况下，可使用预测模型(f)和(g)(见图2)对煤中N、S元素含量进行预测。

3 结 论

(1)基于主成分—三元线性回归分析的Cd、Hd和Od预测模型具有较好的适应性和较广的适应范围；

(2)基于主成分—三元线性回归分析的Nd和Sd预测模型的适应性较差，即以主成分—三元线性回归分析法预测煤中的Nd和Sd是失效的；

(3)基于主成分—BP网络的Nd和Sd预测模型的适应性较主成分—三元线性回归分析时有大幅提升。然而煤中N和S元素含量少、赋存形式过于复杂，即便是具有高度非线性泛化能力的BP网络，也未能精准预测煤中N和S元素含量。