基于Orcaflex的浮式防波堤水动力分析

黄 栋，包雄关，冯宏祥，费殷怡

(宁波大学 海运学院，宁波 315211)

防波堤作为码头重要组成部分，对减小波浪侵蚀、保护港内水域的平稳和其他水工建筑物，确保船只进出、停泊与装卸作业安全方面具有重大作用，因此，分析浮式防波堤运动性能，保证其安全显得至关重要。

毛伟清等[1]利用Frank源汇分布法和Grim切片理论分析在波浪作用下浮式防波堤的消波性能并预报了浮式防波堤在不规则波中的消波性能。周效国等[2]利用试验对透空式防波堤进行了全面的分析，并说明其在港口建设中的应用情况。董国海等[3]提出新式板-网浮式防波堤，并探索平板刚度、平板宽度、网衣数目等变量对消波效果的影响。贺大川等[4]发明水下板式-浮筒型防波堤，并分析其水动力特性，并说明该结构形式浮式防波堤具有较好的消波性能。张宁川等[5]利用流体界面捕捉的方法，探究潜式双层水平板型防波堤与海浪的相互影响。嵇春艳等[6]利用试验把不同类型浮式防波堤的消波性能和运动响应特性进行对比，得出浮式防波堤的最优形式。J.N.Newman[7]通过对两个相同浮式防波堤在刚性连接和铰连接情况下运动响应特性分析，得出铰连接运动特性优于刚性连接情况。S.A.Sannasira等[8]利用试验分析浮筒式浮式防波堤在不同锚泊形式下的运动响应特性和系泊缆张力情况。E.Luca[9]利用试验分析锚链在不同布置形式的情况下对浮式防波堤的影响。E.Louko等[10]利用试验分析包含多个浮体的浮式防波堤的消波和结构响应特性。Koutandos等[11]分别利用有限差分法和边界元法对浅水和中等水深时的固定和垂荡浮式防波堤的消波性能以及受力情况进行计算。国内外文献主要针对防波堤防波性能进行研究，对其强度及运动特性研究较少，本文则通过对浮式防波堤运动特性及系泊缆有效张力进行研究，并根据近几年学者的研究成果进行比对，确保本模型的准确性，对浮式防波堤在实际工程中的应用具有较好参考价值。

1 基本理论

该浮式防波堤有浮筒等刚性部件和锚缆等柔性部件。对于刚性部分，依据刚体运动学建立运动方程；对于柔性部分，则采用凝集质量法建立其运动方程,浮式防波堤在重力FW、浮力FB、惯性力FI、波流载荷曳力FD以及张力FT等载荷作用下偏移S，此时结构的运动方程为

(1)

式中：ρ为水密度；v为排水体积；Cm为附加质量系数。

对于锚缆等这类挠性小尺度结构物可忽略结构对波浪的影响，常采用Morison公式来统一计算拖曳力，OrcaFlex中拓展后的Morison公式为

(2)

式中：F为波浪载荷；△=ρv为排水量；aw为水质点绝对加速度；ar为水质点相对于结构物的加速度；vr为水质点相对于结构物的速度；CD为拖曳力系数；A为拖曳投影面积。

OrcaFlex 中有效张力表达式如式(3)所示

Te=Tw+P0A0-PiAi

(3)

式中：Te为有效张力；P0为外部压力；A0为管线横截面积；Pi为内部压力；Ai为内管横截面积。特别地，缆索Pi与Ai均为零。相邻两节点间壁张力与有效张力相对关系如图1所示。

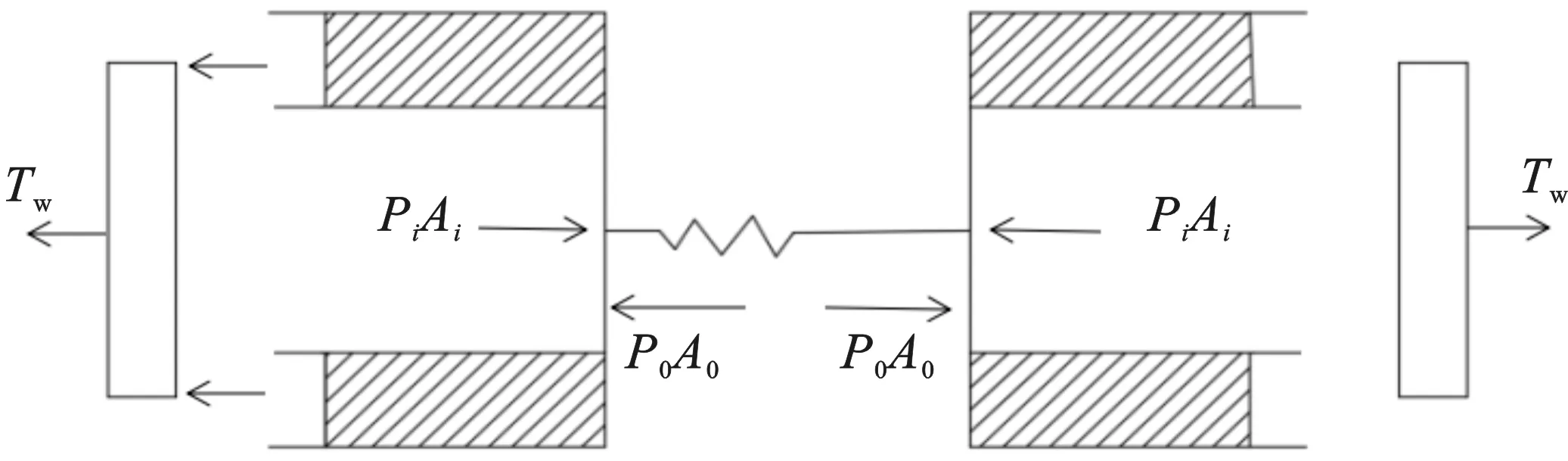
图1 有效张力示意图Fig.1 Schematic diagram of effective tension

图中Tw表示壁面张力，表达式为

Tw=EAε-2v(P0A0-PiAi)+EAe(dL/dT)/L0

(4)

式中：EAε是由于轴向刚度产生的；-2v(P0A0-PiAi)是由于内部、外部压力产生的(通过泊松比的影响)；EAe是由于轴向阻尼产生的。式中EA为缆索轴向刚度；ε=(L-λL0)/λL0是总的轴向平均应变,λ是分段的伸长系数,L0是分段的原长；v是泊松比；e为阻尼系数；dL/dt是长度增加的速率。由于结构阻尼对缆索的影响较小，一般忽略不计。

2 模型建立

表1 浮式防波堤参数Tab.1 Floating breakwater parameters

根据实际情况需要，本文浮式防波堤由10个60 m长的堤段及9组5 m长的连接段组成，总长度为645 m，宽度为25 m，布置于被保护工程的来流方向。本文中浮式防波堤所在水域为我国南海某水域,根据1979～2017年39 a水文资料统计，仅选取斜浪为67.5°和90°进行分析。在本文模型中，空心浮筒通过软件6D buoy 模块中Towed Fish建立，改变Towed Fish的密度达到与空心浮筒相同作用效果，锚绳和锚链通过软件中Line模块实现，具体参数见表1。本文主要研究浮式防波堤系泊系统性能，因此忽略含有防浪球的防浪网在本模型中的建模。

系泊系统中共有64条系泊缆，对称的分布在浮式防波堤的来流面和背流面。其中两个顶端分别布置一组系泊缆，每组2根系泊缆，来减弱浮式防波堤小幅值纵荡运动，另外56根均匀分布在防波堤的两侧，主要用来减弱防波堤的横荡、垂荡和横摇运动，平面布置如图2所示。系泊半径为150 m，水深40 m，系泊缆与海底的夹角为14.931°，如图3所示。

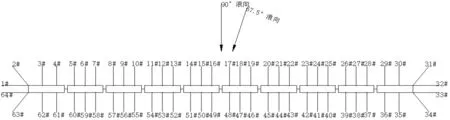
图2 浮式防波堤示意图Fig.2 Floating breakwater schematic

3 结果分析

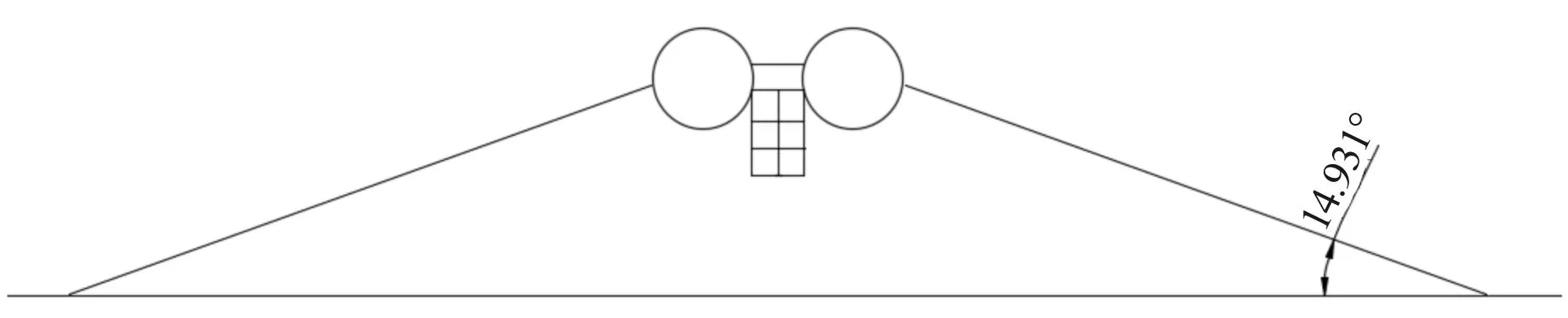
图3 浮式防波堤侧视图Fig.3 Floating breakwater side view

浮式防波堤在工作的时候会产生6个自由度的运动相应，分别为横荡(Sway)、纵摇(Pitch)、垂荡(Heave)、横摇(Roll)、纵荡(Surge)和艏摇(Yaw)。图4给出了在横浪和斜浪以及1#和64#缆失效作用下，浮式防波堤整体运动特性。在90°横浪作用时，纵荡运动最大响应幅值为1.8 m，为水深的4.5%；横荡运动最大响应幅值为1.55 m，为水深的3.9%；垂荡运动最大响应幅值为6.5 m，为水深的16.25%；横摇运动最大响应幅值为6.5°；纵摇运动最大响应幅值为0.55°；艏摇运动最大响应幅值为0.14°；在67.5°斜浪作用时，纵荡运动最大响应幅值为2.5 m，为水深的6.25%；横荡运动最大响应幅值为0.6 m，为水深的1.5%；垂荡运动最大响应幅值为2.8 m，为水深的7%；横摇运动最大响应幅值为1.5°；纵摇运动最大响应幅值为0.25°；艏摇运动最大响应幅值为0.075°。

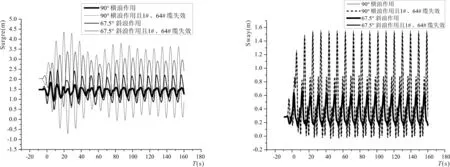
4-a 纵荡时历曲线4-b 横荡时历曲线

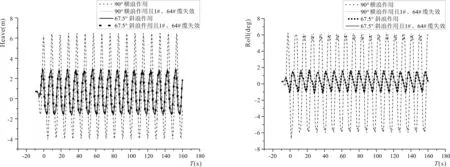
4-c 垂荡时历曲线4-d 横摇时历曲线

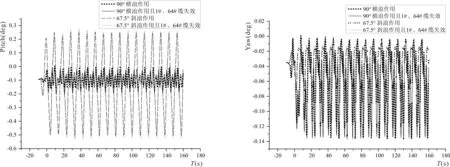
4-e 纵摇时历曲线4-f 艏摇时历曲线图4 浮式防波堤运动特性Fig.4 Floating breakwater movement characteristics

表2 系泊缆锚泊点有效张力Tab.2 Mooring line anchor point effective tension

一般情况下，与浮式防波堤背浪面系泊缆张力相比，防波堤迎浪面的系泊缆张力更大,因此选取防波堤迎浪面系泊缆作为主要的研究对象，又由于系泊缆对称性张力相等，所以在分析90°横浪作用和67.5°斜浪作用下系泊缆有效张力时，选取27#、30#、31#、32#、33#、34#、35#和38#系泊缆为主要研究对象。由图2知，27#和30#缆为迎流缆，31#、32#、33#和34#缆为浮式防波堤端侧缆，35#和38#缆为背流缆，其锚泊点所受有效张力时历曲线如图5，有效张力最大值和均值见表2。由表2数据，在90°斜浪作用下，系泊缆有效张力明显大于67.5°斜浪作用下系泊缆有效张力，且31#、32#、33#和34#系泊缆无论经历横浪作用还是斜浪作用，有效张力比迎流缆和背流缆高8 000 kN左右，因此要注意浮式防波堤两端8根系泊缆强度问题。

5-a 27#缆有效张力5-b 30#缆有效张力

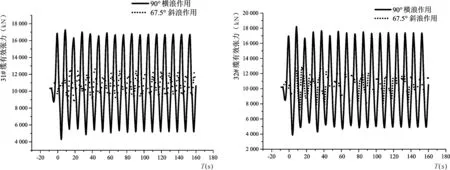
5-c 31#缆有效张力5-d 32#缆有效张力

5-e 33#缆有效张力5-f 34#缆有效张力

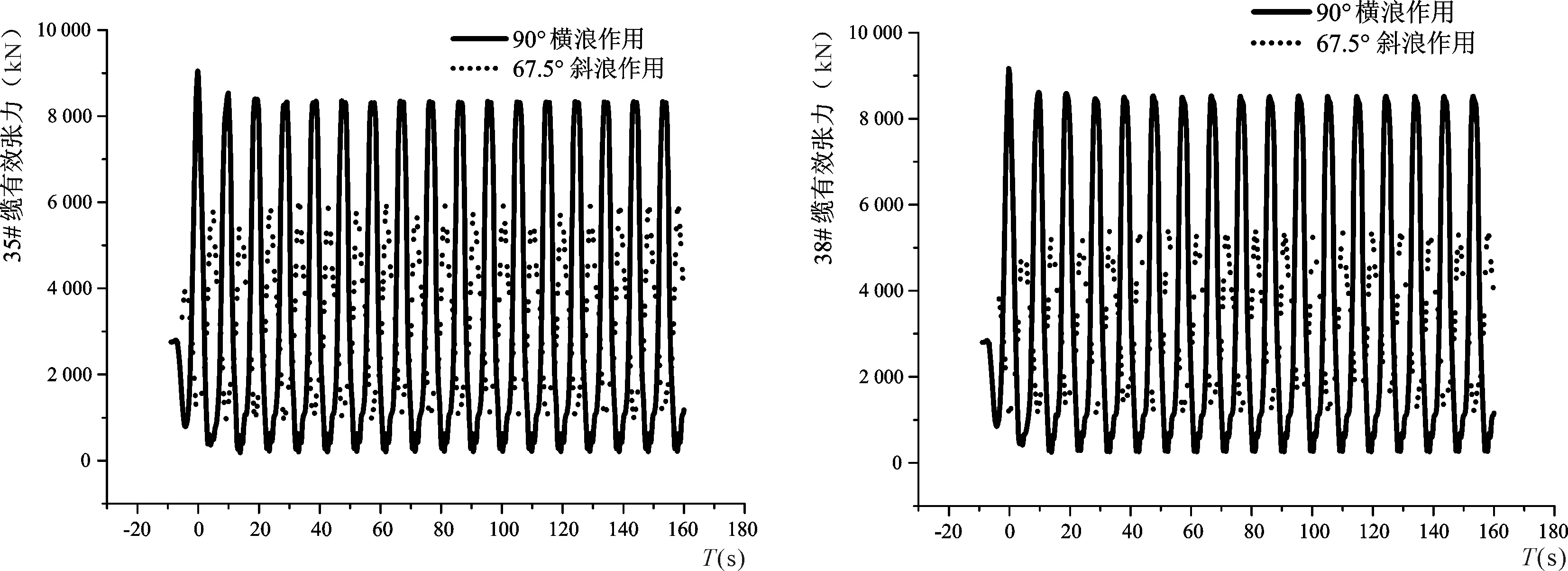
5-g 35#缆有效张力5-h 38#缆有效张力图5 系泊缆锚泊点有效张力时历曲线Fig.5 Mooring line mooring point effective tension calendar curve

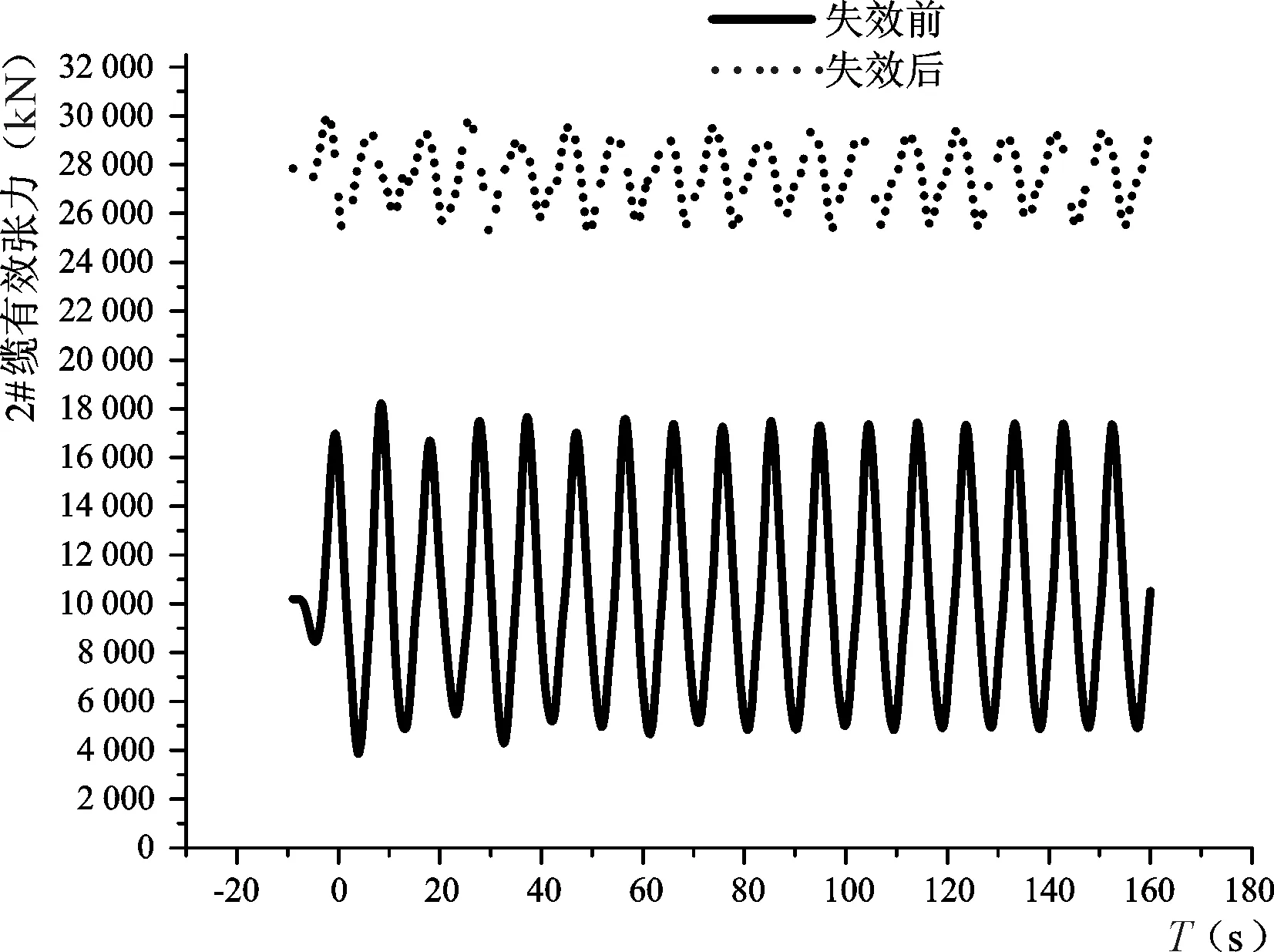
图6 2#缆锚泊点有效张力时历曲线Fig.6 2 # Cable anchor point effective tension calendar curve

考虑浮式防波堤两端会有系泊缆失效情况，在分析系泊缆有效张力时，本文就1#和64#缆失效的情况进行研究，浮式防波堤主体水动力性能如图4。由图4-a可知，当浮式防波堤1#和64#缆失效后，对浮式防波堤6个自由度响应影响最大的是纵荡，对其他响应影响不强，90°横浪作用下，失效后响应幅值增加478%，67.5°斜浪作用下，失效后响应幅值增加50%。且失效前后相邻系泊缆锚泊点有效张力对比如图6，有效张力极值增加180%。

4 结论

本文通过大型水动力分析软件Orcaflex，对浮式防波堤进行建模，分析其在不同波浪方向下浮式防波堤主体的运动响应及系泊缆有效张力，并分析在一端系泊缆失效情况下，对浮式防波堤运动特性和系泊缆张力的影响，得出以下结论：

(1)在横浪作用下，浮式防波堤整体纵摇和艏摇运动响应极小，其主要运动响应是纵荡、横荡、垂荡和横摇。在斜浪作用下，浮式防波堤整体的纵摇和艏摇运动响应比横浪条件下大很多，但对于横荡、纵荡、垂荡和横摇运动响应，横浪的影响却远远大于斜浪。此外，斜浪作用时，浮式防波堤整体的3个平动响应相差不大，3个旋转运动中横摇运动响应最大，纵摇和艏摇运动响应较小；

(2)浮式防波堤两侧系泊缆有效张力均远远小于两端系泊缆有效张力，因此浮式防波堤两端系泊缆强度要适当提高，且在横浪作用下最大系泊缆张力远远大于斜浪作用下最大系泊缆张力，这说明该系泊系统对斜浪的承受力要优于横浪；

(3)当端侧系泊缆发生失效，相邻系泊缆张力将大大增加，且纵向运动响应也会大大提高，因此当发生类似系泊缆失效事故，应及时修复或提高系泊缆的密度。