基于PUF的Logistic混沌序列发生器

黄春光，程海，丁群



基于PUF的Logistic混沌序列发生器

黄春光，程海，丁群

（黑龙江大学电子工程学院，黑龙江 哈尔滨 150080）

由于Logistic非线性混沌系统在一定的参数下，具有初值敏感性和拓扑复杂性等特点，因此Logistic混沌系统可以作为随机序列信号发生器。同时由于集成电路在生产、制作的过程中，即使采用完全相同的设计方法和制造工艺，也会在器件上产生不可控的微小差异，这些微小差异便成为集成电路不可克隆的基础。基于此特点，提出了一种基于可编程逻辑阵列（FPGA）的双输出查找表（LUT）结构的物理不可克隆函数（PUF）的Logistic随机混沌序列信号发生器，该混沌序列发生器具有物理的唯一性，能够有效地抵抗对于系统的复制和攻击。将该系统在Xilinx公司的FPGA开发板上进行测试和验证，结果表明，同样的电路结构和配置文件在不同的FPGA开发板上能够产生不同的随机序列，提高了混沌序列的随机性。

Logistic混沌系统；物理不可克隆函数；序列发生器；流密码

1 引言

随着通信技术的飞速发展及互联网络和移动网络的广泛使用，人们越来越关注信息的安全。混沌系统由于具有初值敏感性和拓扑复杂性等特点，得到了广大研究人员的关注[1]。

混沌系统是指在一个确定性的系统中，存在着随机的不规则运动，这种运动具有不确定性、不可重复性以及不可预测性，是非线性动力系统的固有特性。Logistic混沌映射是一种一维混沌系统，当该系统的参数在一定的范围内时，系统会进入混沌状态。由于混沌特性的存在，Logistic混沌映射系统可以应用在随机信号发生器上。为了便于数字电路和FPGA应用Logistic混沌系统，通常采用离散的Logistic混沌映射系统进行设计和开发[2-3]。由于离散混沌系统具有状态随机性和初值敏感性等特点，因此可以将其应用到数字图像加密[4]、随机数发生器[5]以及数字认证等相关领域。

物理不可克隆函数（PUF, physical unclonable function）是一种对集成电路芯片在制造过程中产生的细微差异进行放大并使其产生独一无二的物理不可克隆特征的函数。大多数物理不可克隆函数的实现是通过计算和分析电路的时延信息的差异进行设计的。想要对物理不可克隆函数模块进行复制，需要复制相同的逻辑单元、相同的布局布线，同时在物理电路上进行精确的设计，才能得到相同的结果。但是对于具体的物理电路而言，电路结构和布局布线的差异是由电路自身的物理参数决定的，无法进行克隆复制，因此物理不可克隆函数提供了一种可以在相同的电路结构上产生不同的差异的模块。由于PUF具有基于器件特征的固有随机性，很多研究人员将PUF应用到设备的认证环节[6]和通信环节[7]。

可编程逻辑阵列（FPGA, field-programmable gate array）是一种可编程的芯片，能够根据用户的需求通过软件手段进行更改、配置内部连接结构和逻辑单元、完成指定设计功能的数字电路。由于可编程逻辑阵列具有开发简单方便、实现效率高等优点，已广泛应用到电路设计、嵌入式系统等各个领域。在进行可编程逻辑阵列应用开发的过程中，可以使用芯片提供商提供的开发软件进行逻辑电路的设计和仿真，然后下载到可编程逻辑阵列中。在使用过程中，可以将生成的比特流数据下载到相应的逻辑电路中，完成对于系统的配置。由于电路结构相同，可以将相同的比特流下载到不同的FPGA逻辑电路中，得到相同的功能。由于物理不可克隆函数的存在，即使相同的配置文件，也会产生不同的结果，因此可以对设备进行识别和身份确认。

FPGA具有配置灵活、设计方便等特点，非常适合电路设计。Dabal等[8]利用Xilinx公司的FPGA设计了基于Logistic混沌系统的随机序列，作为流密码发生器。Wang等[9]利用Simulink工具设计了基于FPGA的混沌序列信号发生器，并对相关性进行分析。但是，由于数字Logistic混沌系统产生的序列和器件结构无关，因此容易被复制、攻击和探测。基于此，本文设计了一种基于物理不可克隆函数的Logistic混沌序列发生器，利用FPGA硬件结构的细微差异产生基于器件特征的混沌随机序列，并利用FPGA中的基本单元——查找表（LUT, look-up-table）在不同器件上传输时延的细微差异进行设计，所产生的混沌序列与物理器件相关，相同的电路在不同的FPGA器件上可以产生完全不同的结果。该系统可以作为安全设备的终端，利用在服务器上存储的硬件特征完成设备的验证或数据的加密传输。

2 相关工作

2.1 国内外发展

目前，在通信领域、视频传输、网络通信和个人消费电子产品等相关领域都需要基于FPGA加密技术的数字认证环节[10]。Wang等[11]提出了一种基于FPGA公钥与私钥对的知识产品保护方案。Guajardo等[12]设计了一种基于PUF的加密认证系统。Tuncer等[13]利用Logistic混沌系统作为PUF的初始随机向量，然后对Logistic混沌系统的输出进行判断，产生“0”和“1”的随机序列。该系统采用Logistic信号发生器作为PUF的随机输入。由于PUF的状态有限，没有充分利用混沌系统的状态随机性和初值敏感性，而且该系统的PUF模块在四输入单输出的LUT模块上实现，利用率低，因此只对该系统在单个开发板上进行了测试，没有将其应用到其他开发板，以测试PUF的特性。Liu等[14]给出了一种基于碳纳米管的物理不可克隆函数，采用的混沌方程为Lorenz混沌方程，利用碳纳米管工艺的不确定性，生成PUF。但是由于碳纳米管生成的序列位数有限，而且采用模拟电路进行设计，不利于大规模开发和使用。

2.2 物理不可克隆函数

自2002年以来，人们对基于硅电路的PUF电路进行了深入的研究。到目前，研究人员已经提出了各种物理不可克隆的方法，例如，基于随机存储器的PUF、基于触发器的PUF、基于蝴蝶类型的PUF、基于仲裁器的PUF、基于环形振荡器的PUF[15]、基于电路毛刺的PUF[16]等。产生PUF的方法，大体上可以分为2种，介绍如下。

一种为采用随机存储的方式设计的PUF电路。由于存储电路是由一种状态可以改变的双稳态电路组成的，因此存储电路在通电之前会处于一种随机状态。存储电路在通电之后，寄存器上的状态是一种随机状态，此时存储电路上的高低电平可以作为PUF使用。但是对于芯片设计厂商来说，为了避免这种状态的出现，在电路通电之后，会进行强制复位。只有在设计电路时进行单独设计，才能够使用。

另一种为采用时延的方式设计的PUF，利用物理器件上门电路的时延和布线的时延差异进行设计。在实现方式上，主要分为2种，一种是仲裁型PUF，另一种是环形振荡器PUF。

1) 仲裁型PUF

采用2路相同的传输路径，由于集成电路制造工艺的细微差异会产生不同的时延，判决器根据2路传输路径到达时间的差异决定输出是“0”还是“1”，从而产生基于器件自身特点的随机信号。仲裁型PUF的控制端控制信号传输的路径，系统输入端输入同一个脉冲信号，利用控制信号进行路径选择，使信号经过不同的传输路径，根据信号到达仲裁器的先后顺序进行判决。

在PUF设计过程中，需要尽量保证传输路径的长度一致，但是由于物理元件的差异，最终会导致同一个脉冲到达仲裁器的时间不尽相同。如图1所示，仲裁类型PUF利用控制信号（0,1,…）选择信号传输的路径，输入的是同一个脉冲信号，经过不同的路径到达仲裁器，仲裁器根据脉冲信号到达的先后顺序进行判决，决定输出是“0”还是“1”。这类PUF需要的多路选择器级别多、路径长，否则无法分辨到达的先后顺序，即使能够判决，也容易被外界环境干扰。

图1 仲裁型PUF

2)环形振荡器PUF

利用反相器级联形成振荡电路，通过计数器进行计数。由于物理电路结构的微小差异，经过多次计数，2个计数器的结果不尽相同，然后通过比较器，得到最终的结果。

图2中与门作为控制端，控制环形振荡器PUF的起振和停止。与门和后面的多个反相器相连接，构成一个连续反向的环。该环形振荡器产生的脉冲信号作为计数器的时钟，进行计数。计数器设定计数的截止上限，当其中任意一个计数器计数达到上限，则环形振荡器停止工作。在进行布局布线过程中，要求保证路径长度一致。比较器通过比较2个计数器数值的大小，输出“0”或“1”。

图2 环形振荡器PUF

在环形振荡器PUF中，如果反相器的个数为奇数，需要使用与门作为控制模块，控制环形振荡器的工作状态；如果环形振荡器中反相器的个数为偶数，则采用与非门作为控制模块。

环形振荡器PUF所需的与非门的个数少，相对仲裁型PUF来说占用资源少，外界环境影响小。

2.3 Logistic混沌方程

Logistic方程为混沌系统的经典实例，系统结构简单，便于FPGA设计、实现和验证，同时便于推广到其他混沌系统。

Logistic函数的数学表达式为

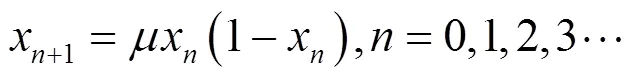
式(2)是Logistic方程的二进制表现形式。其中，为二进制的表现形式，是二进制每一位的值。的位数越大，Logistic方程的精度越好，同时需要的运算量就越大。

3 系统设计

基于环形振荡器的PUF，利用有限个数的反相器，构建一个反馈链。基于仲裁型的PUF，可以利用控制位选择相应的路径，根据判决器的结果产生“0”或“1”。本文提出基于混合型PUF的Logistic序列发生器，同时利用环形振荡器PUF与仲裁型PUF的特点，产生基于物理器件特征的随机数。利用Logistic混沌方程对系统初值的敏感性（如图3所示），初值的细微差异会产生完全不同的变化轨迹。利用Logistic方程的特点，将PUF与Logistic迭代方程相结合，既利用PUF的硬件唯一性，又利用Logistic函数的敏感性，产生与硬件相关的混沌序列，同时在Xilinx公司的7-series FPGA上进行设计和验证。

3.1 基本单元模块

本文采用FPGA进行设计和开发。由于FPGA具有大量的可编程资源，为系统的实现提供了相应的功能模块，既解决了定制电路的不足，又克服了原有可编程器件门电路有限的缺点。Xilinx公司的FPGA具有6输入2输出的LUT模块，有利于多输入多输出的应用模块设计。

Xilinx公司的7-series FPGA的基本单元为CLB，每个CLB由2个SLICE组成，每个SLICE由4个5输入的LUT、3个MUX、一个CARRY和8个FF组成。

如图4所示，Xilinx公司7-series FPGA的每个LUT有6个输入端口，当A6设置为高电平时，可以作为2个5输入的LUT使用，可以有2个输出。在设计过程中，需要对LUT6_2模块进行配置，将其配置为2输入2输出的与门电路和2输入2输出的非门电路。

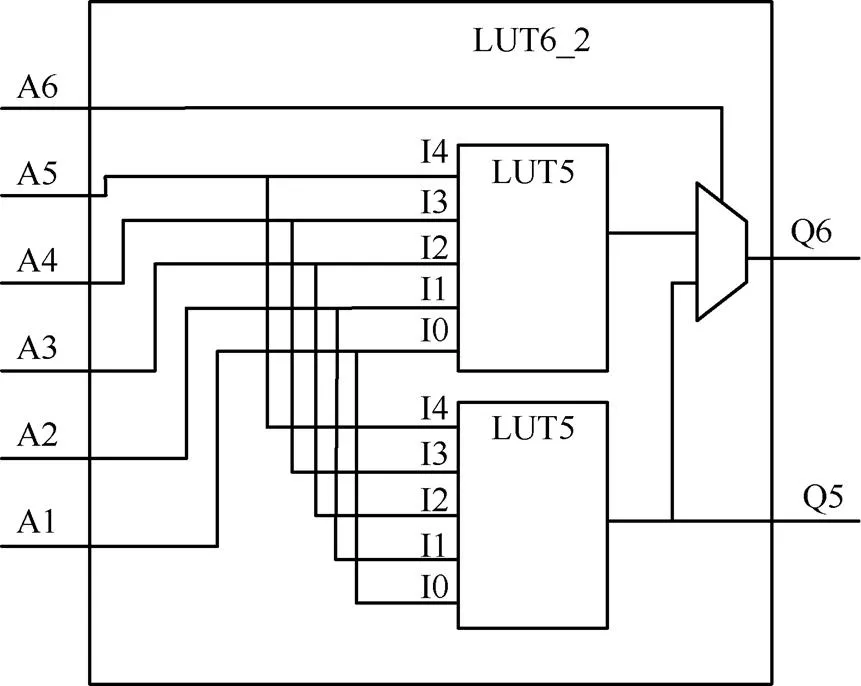
图4 FPGA的基本单元LUT6_2

对于图5中的2输入2输出非门电路，即图中虚线内部的模块，可以用一个LUT6_2进行设计。可以充分利用LUT6_2的2个输出的特性，将A6设置为高电平，而A5和A4输入没有使用，可以配置高电平或低电平，不能悬空使用。在本设计中，A4和A5设置为低电平，这样就可以使用Q5和Q6这2个输出，则电路等效如图5所示。

图5 基于LUT6_2的双路非门电路

每个模块有3个输入，其中，A3作为选择信号，A2和A1作为数据的2个输入端口，此时，该电路模块为3输入2输出的功能模块。根据真值表进行计算，可以得到LUT6_2的配置码为0x0000c0a0_0000a0c0，此时LUT可实现双路非门和路径选择的功能。

同理，将LUT6_2设计为2输入2输出的与门时，每个模块有4个输入，其中，A6为高电平，A5为低电平，A4作为使能信号，A3作为选择信号，A2和A1作为数据的2个输入端口，则根据电路的功能设置相应LUT的数值。根据真值表进行计算，可以得到LUT6_2的配置码为0x00000035_ 00000053，此时LUT可以实现双路与门及路径选择的功能，如图6所示。

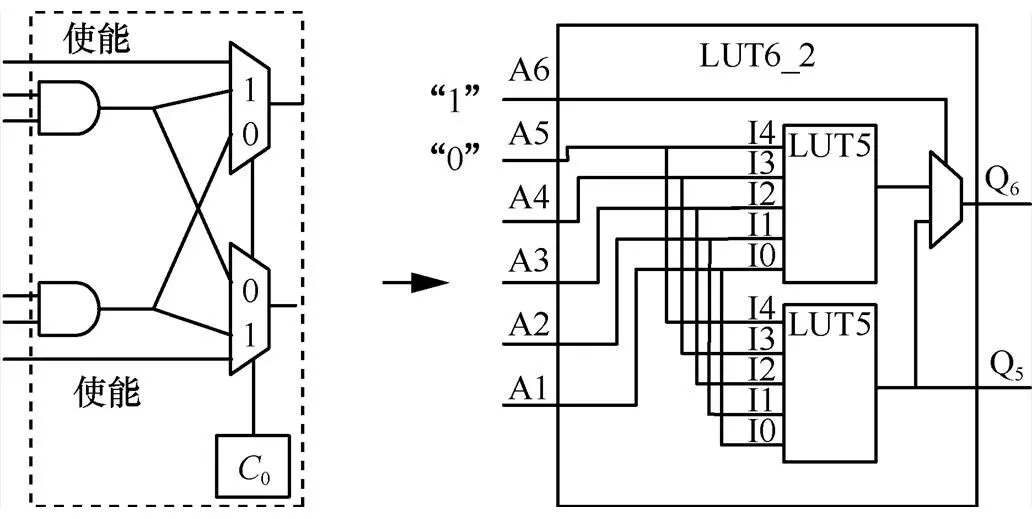
图6 基于LUT6_2的双路与门电路

3.2 系统框图

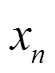
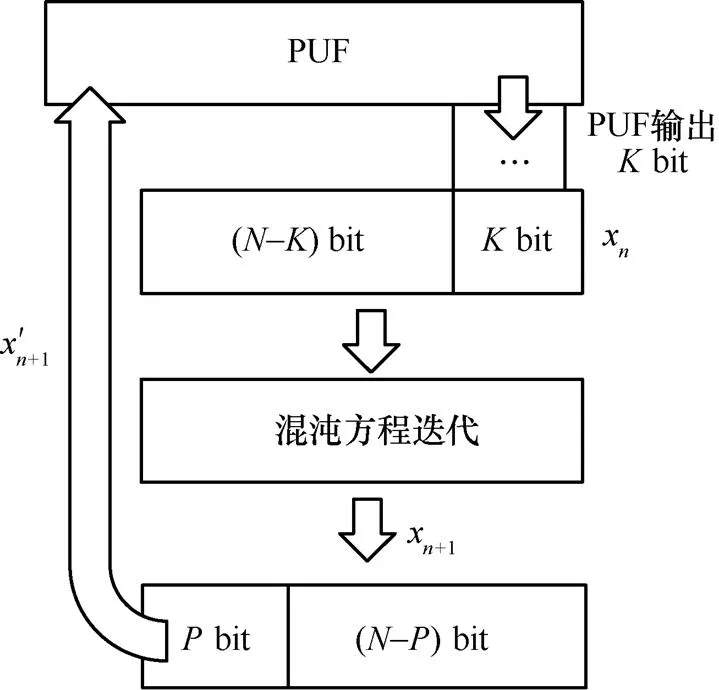
图8 系统工作流程

系统工作状态机如图9所示，分为5个步骤。

图9 系统工作状态机

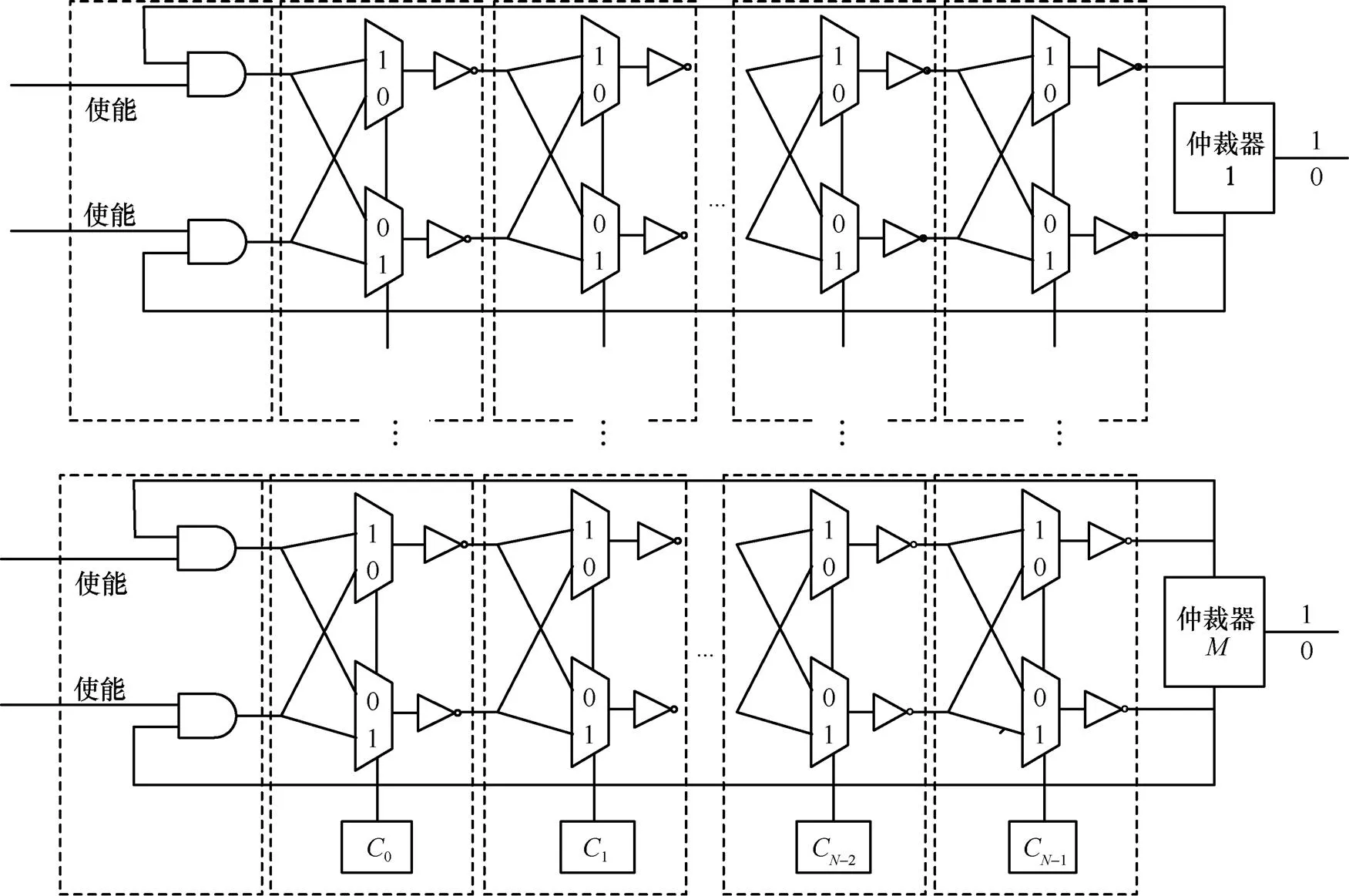
图7 系统框图

步骤1 设置系统的初值，PUF的结构有个控制端，用来选择PUF的不同路径。由于PUF的特点，不同的PUF所产生的结果不完全一样。

步骤2 利用PUF模块生成bit，将bit传递给Logistic混沌系统。

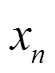
4 系统分析与测试

在本文系统中，由于PUF的存在，使原来混沌系统无法迭代到的点重新成为系统的初值，破坏了离散混沌系统的周期性，为了测试基于PUF的Logistic混沌序列发生器的特性，采用Xilinx公司的7-series FPGA开发板进行测试，并对序列发生器的相关特性进行了分析和讨论。

4.1 实验环境

本文在Xilinx公司的7-series FPGA上设计了基于物理不可克隆函数的Logistic混沌序列发生器，设计软件采用Xilinx公司的vivado 2017.4版本进行设计开发，并利用vivado自带逻辑分析仪进行数据测试和分析。在实验过程中，对4块同样的FPGA开发板进行测试，通过XDC文件对模块的具体位置和走线利用约束条件进行限定，同时将PUF布置到FPGA的不同位置进行测试。

本系统利用LUT6_2设计了32路PUF，通过对32路PUF的计数器输出的数值进行比较，得到32 bit的输出。

4.2 实验数据

在实验过程中，同样的配置代码在不同的FPGA开发板上的结果并不相同。首先，相同的Logistic初始向量作用到PUF上，不同的开发板得到的结果如表1所示，结果呈现出随机性。

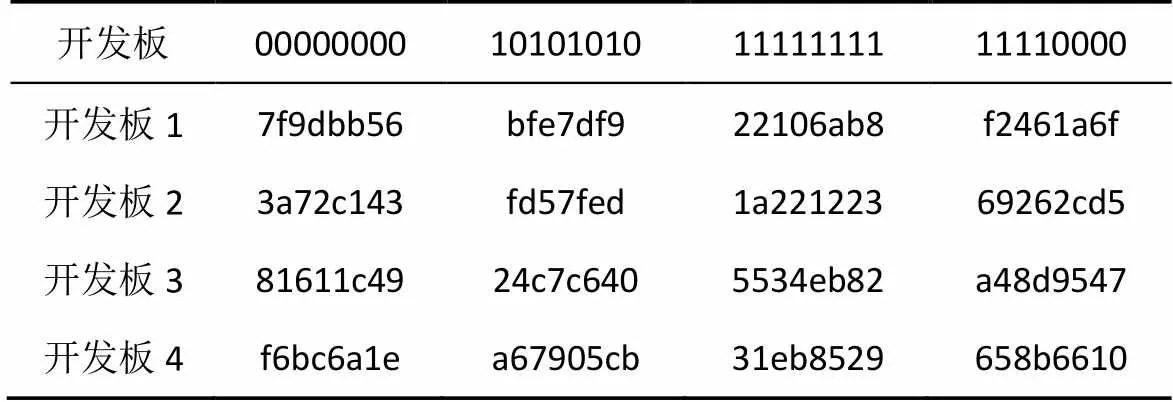
表1 不同开发板在相同配置下的输出结果

系统的硬件开销如表2所示。由于系统采用LUT6_2的单元电路，每个单元模块包括6个输入和2个输出，因此每个LUT模块可以实现2路PUF电路，由于LUT模块具有6个输入端口，可以选择其中一个端口作为控制端口，使得硬件的利用率得到提升。Tuncer等[13]使用LUT4_1模块，每个模块可以实现一路PUF电路，利用率低。

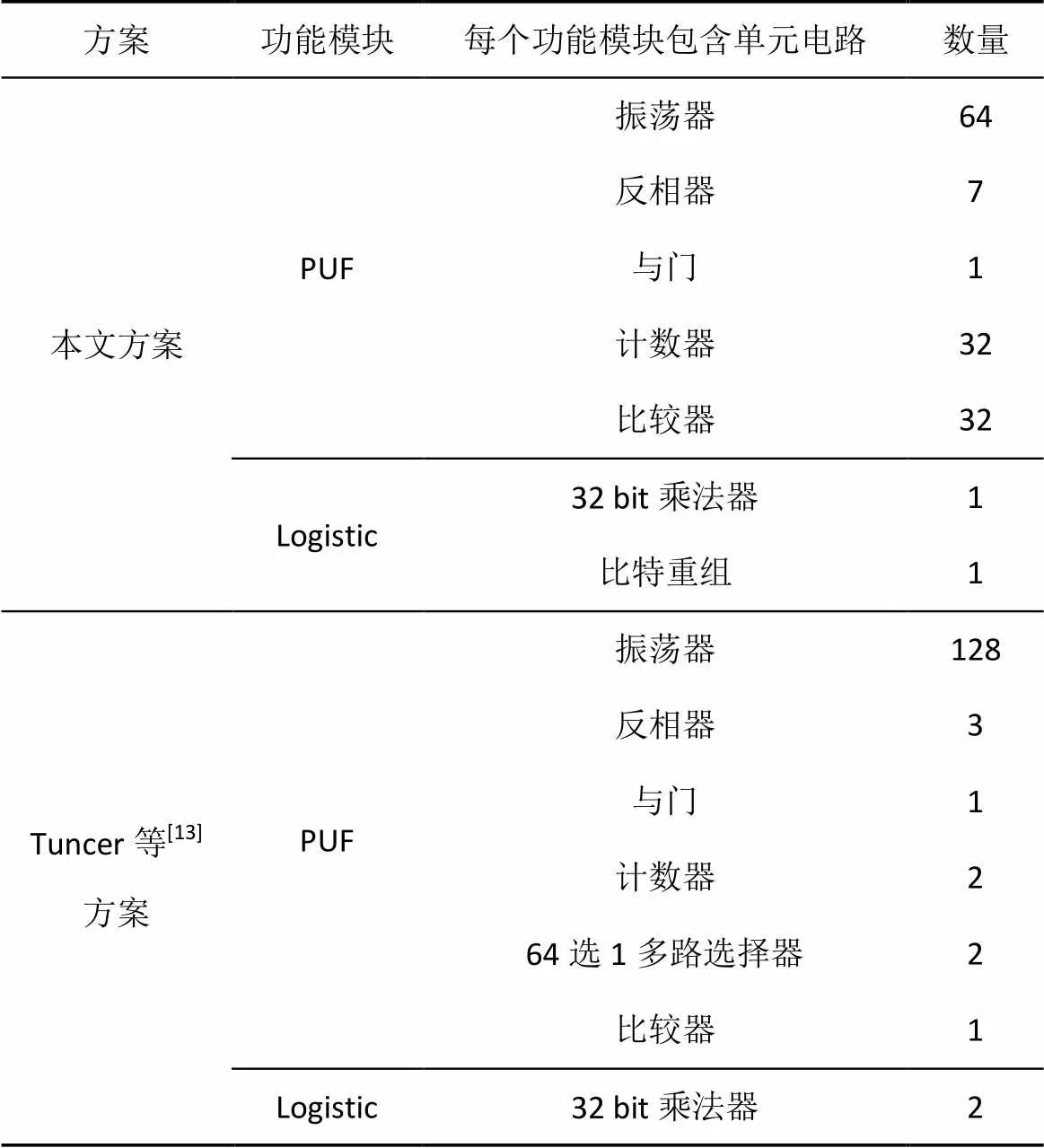
表2 硬件开销说明

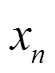
图10 PUF单元的布局布线

4.3 数据分析

4.3.1 相关性分析

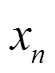
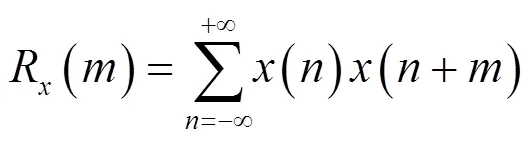
通过对混沌序列发生器的输出进行分析和设计，对于原始的Logistic混沌系统，采用32 bit的精度进行计算，自相关函数如图11所示，对于不同的Logistic初值，系统会出现一些周期现象。

如果采用基于PUF的Logistic混沌系统进行设计，可以阻止Logistic混沌系统周期现象的出现。同时，由于PUF系统的存在，使Logistic混沌轨道上无法迭代到的点可以成为系统的初值进行计算，改善了系统的周期性，如图12所示，系统不存在明显的周期性现象。

4.3.2 随机性分析

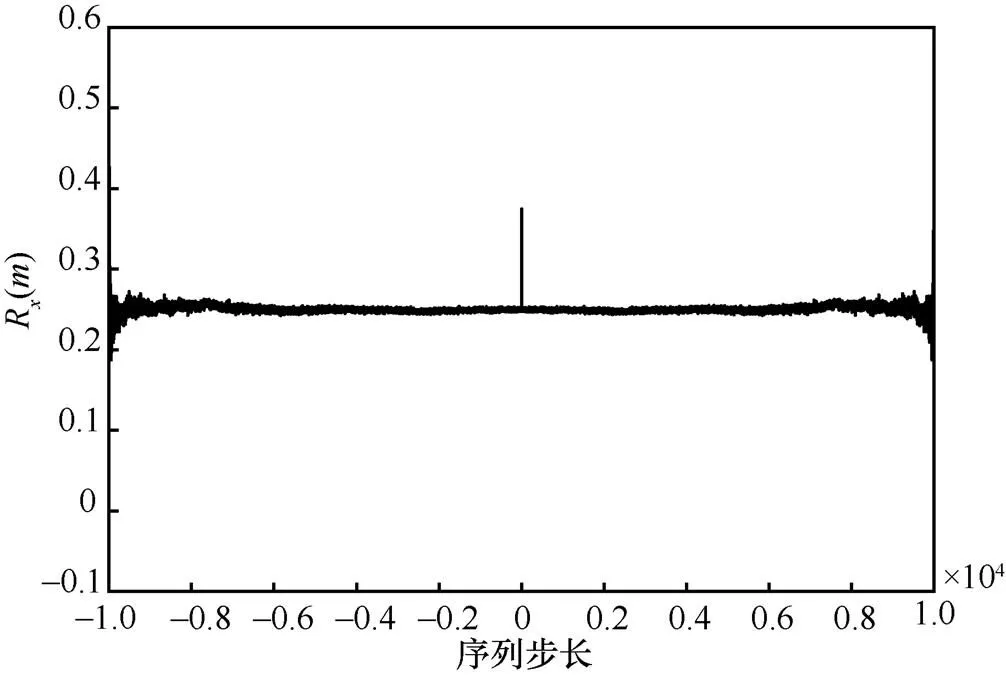
图12 基于PUF的Logistic序列自相关函数

表3 评价指标P值的对比结果

5 结束语

本文提出了一种基于物理不可克隆函数（PUF）的Logistic混沌序列发生器，利用FPGA器件的LUT以及传输路径在生产过程中的工艺差异进行设计，所以即使同样配置码下载到不同的FPGA开发板上，产生的结果也不同。首先利用Xilinx的FPGA中的LUT6_2设计了2路PUF结构，相对于传统的FPGA而言，节省了一半的资源；然后利用PUF产生的随机数对Logistic混沌系统进行优化，设计了Logistic混沌序列信号发生器。该序列发生器产生的序列与物理器件的特性相关，利用物理器件的特征参数作为序列发生器的原始密钥，保证了序列发生器的唯一性。NIST检验表明，混沌序列信号发生器产生的序列满足随机性的要求。

[1] SBIAA F, BAGANNE A, ZEGHID M, et al. A new approach for encryption system based on block cipher algorithms and Logistic function[C]//International Multi-Conference on Systems, Signals & Devices. 2015: 1-5.

[2] KANSO A, SMAOUI N. Logistic chaotic maps for binary numbers generations[J]. Chaos Solitons & Fractals, 2009, 40(5): 2557-2568.

[3] 蔡丹, 季晓勇, 史贺, 等. 改进分段 Logistic混沌映射的方法及其性能分析[J]. 南京大学学报(自然科学), 2016, 52(5): 809-815. CAI D, JI X Y, SHI H, et al. Method for improving piecewise Logistic chaotic map and its performance analysis[J]. Journal of Nanjing University, 2016, 52(5): 809-815.

[4] XU L, LI Z, LI J, et al. A novel bit-level image encryption algorithm based on chaotic maps[J]. Optics & Lasers in Engineering, 2016, 78(21): 17-25.

[5] 宣蕾, 闫纪宁. 基于混沌的“一组一密”分组密码[J]. 通信学报, 2009, 30(Z2): 105-110.XUN L, YAN J N. The “one group one cipher” cryptograph of block cipher based on chaotic[J]. Journal on Communications, 2009, 30(Z2): 105-110.

[6] 王俊, 刘树波, 梁才, 等. 基于PUF和IPI的可穿戴设备双因子认证协议[J]. 通信学报, 2017, 38(6): 127-135. WANG J, LIU S B, LIANG C, et al. Two-factor wearable device authentication protocol based on PUF and IPI[J]. Journal on Communications, 2017, 38(6): 127-135.

[7] 郭渊博, 张紫楠, 杨奎武. 基于PUFS的不经意传输协议[J]. 通信学报, 2013, 34(Z1): 38-43. GUO Y B, ZHANG Z N, YANG K W. Oblivious transfer based on physical unclonable function system[J]. Journal on Communications, 2013, 34(Z1): 38-43.

[8] DABAL P, PELKA R. FPGA implementation of chaotic pseudo-random bit generators[C]//Mixed Design of Integrated Circuits and Systems. 2012: 260-264.

[9] WANG H J, SONG B, LIU Q, et al. FPGA design and applicable analysis of discrete chaotic maps[J]. International Journal of Bifurcation & Chaos, 2014, 24(4): 917-921.

[10] ADAMO O, MOHANTYZ S P, KOIUGIANOS E, et al. VLSI architecture and FPGA prototyping of a digital camera for image security and authentication[C]//Region 5 Conference. 2006: 154-158.

[11] WANG Y, RENFA L I. FPGA based unified architecture for public key and private key cryptosystems[J]. Frontiers of Computer Science, 2013, 7(3): 307-316.

[12] GUAJARDO J, KUMAR S S, SCHRIJEN G J, et al. FPGA intrinsic PUFs and their use for IP protection[C]//International Workshop on Cryptographic Hardware and Embedded Systems. 2007: 63-80.

[13] TUNCER T. The implementation of chaos-based PUF designs in field programmable gate array[J]. nonlinear dynamics, 2016, 86(2): 1-12.

[14] LIU L, HUANG H, HU S. Lorenz chaotic system based carbon nanotube physical unclonable functions[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2017, PP(99): 1.

[15] KUMAR S. The buttefly PUF : protecting IP on every FPGA[C]//IEEE International Workshop on Hardware Oriented Security and Trust. 2008.

[16] 庞子涵, 周强, 高文超, 等. 高效能FPGA毛刺PUF设计与实现[J]. 计算机辅助设计与图形学学报, 2017, 29(6): 1135-1144. PANG Z H, ZHOU Q, GAO W C, et al. Design and implementation of high efficiency PUF circuit on FPGA[J]. Journal of Computer-Aided Design & Computer Graphics, 2017, 29(6): 1135-1144.

[17] CHENG H, SONG Y, HUANG C, et al. Self-adaptive chaotic Logistic map: an efficient image encryption method[J]. Journal of Internet Technology, 2016, 17(4): 743-752.

Logistic chaotic sequence generator based on physical unclonable function

HUANG Chunguang, CHENG Hai, DING Qun

Electronic Engineering College of Heilongjiang University, Harbin 150080, China

Logistic nonlinear chaotic system has many good characters such as initial value sensitivity and topological mixing in the some parameter condition, which is used to create the random sequence signal generator. Because of the attributions of randomness and uniqueness even under the exact, the same circuit layouts and manufacturing procedures, there is still an instinct unclonable difference in each integrated circuit. Therefore, a new sequence stream generator was proposed based on Logistic chaotic system and physical unclonable function designed by double output look-up-table (LUT). The output of the Logistic sequence generator was associated with a specific physical circuit. This kind of sequence generator could resist an attack such as the replication of the keys of the system. The system was designed and tested on the Xilinx FPGA board. The results show that the same architecture of the circuit and the same config file operated on the different FPGA developing board can generate the total different random chaotic sequence stream and improve the randomness of the stream.

Logistic chaotic system, physical unclonable function, random number generator, stream ciphe

TP301

A

10.11959/j.issn.1000−436x.2019064

2018−05−14；

2018−08−16

丁群，qunding@aliyun.com

国家自然科学基金资助项目（No. 61471158, No.61571181）

The National Natural Science Foundation of China (No.61471158, No.61571181)

黄春光（1980− ），女，黑龙江哈尔滨人，黑龙江大学讲师，主要研究方向为保密通信、信息安全。

程海（1979− ），男，黑龙江哈尔滨人，黑龙江大学副教授、硕士生导师，主要研究方向为保密通信、信息安全。

丁群（1957− ），女，黑龙江哈尔滨人，黑龙江大学教授、博士生导师，主要研究方向为保密通信、信息安全。