口碑参与模式下移动众包网络的用户博弈研究

曾锋，王润华，彭佳，陈志刚



口碑参与模式下移动众包网络的用户博弈研究

曾锋1，王润华1，彭佳2，陈志刚1

（1. 中南大学计算机学院，湖南 长沙 410000；2.空中交通管理系统与技术国家重点实验室，江苏 南京 210000）

研究了口碑参与模式下参与用户之间的博弈行为，探究个体利益最大化的最佳策略。首先，给出了口碑参与模式下移动用户行为交互场景和相关定义，提出的移动用户效应函数不仅考虑了用户的数据贡献量，还考虑了用户邀请与合作因素，能激励用户之间相互合作；然后，基于博弈论斯塔克伯格模型分析了口碑参与模式下用户的博弈过程，把用户之间的行为交互分成两级博弈过程，应用逆向归纳法分析得出一级和二级博弈中用户的最佳对策，并获得了斯塔克伯格均衡；最后，证明了斯塔克伯格均衡的存在唯一性，提出了计算斯塔克伯格均衡的算法。数值实验结果验证了用户效应函数的合理性和斯塔克伯格均衡的存在唯一性。

移动众包；口碑参与模式；博弈论；斯塔克伯格模型

1 引言

众包是利用群体智慧来解决各种复杂任务的一种市场模式[1]。随着移动智能设备的日益普及，依靠如GPS（global positioning system）、摄像头、麦克风等丰富的外部设备和传感器，终端可以在移动中完成众包任务，称之为移动众包，移动众包正成为一种新的众包范例[2]，其市场有三要素：众包人、众包平台和移动用户。众包人通过众包平台向外界发布众包任务，移动用户感知并考虑参与完成众包任务。目前，移动众包主要应用于解决大规模、复杂的社会感知问题，如环境监控、健康检测、城市管理、公共安全和智能交通等问题[3-4]。移动众包在解决大规模的社会问题上具有快速、高效及便捷的优势，因此得到了工业界和学术界的广泛关注。

移动众包市场存在2种任务感知方式，即直接参与模式（DM，direct mode）和口碑参与模式（WoM，word of mouth mode）[5]。DM模式指移动用户直接通过众包平台感知众包任务，这种参与方式下移动用户间不存在直接的信息交互，移动用户群的组建效率不高。WoM模式指已经感知众包任务的移动用户利用社交网络、机会网络或其他途径来邀请其他移动用户参与众包任务。与DM模式相比，WoM模式下用户可以快速地向外扩散众包任务，缩短了众包用户群的建立时间，移动用户间能进行直接的信息交流，形成邀请与被邀请的直接利益联系。WoM模式具有良好的灵活性，依赖不同的邀请渠道可以满足不同类型的众包任务要求，如WoM模式基于社交网络实现用户邀请在短时间内扩散众包任务并建立移动用户群，这满足了具有时效性的众包任务要求；当众包任务具有地理位置约束时，移动用户通过机会性相遇扩散众包任务邀请，众包人招募满足任务地理位置要求的移动用户，这保证了移动用户群的有效性。目前，已有许多国内外学者针对移动众包展开研究，然而大部分工作主要考虑DM模式下的移动众包市场，忽略了WoM模式为移动众包市场带来的有利影响，针对WoM模式展开移动众包研究将会获得更好成果。

在WoM模式移动众包市场中，众包人发布众包任务到众包平台，部分移动用户以DM模式感知众包任务。成功感知众包任务的移动用户决定贡献多少数据量，也决定是否向外发送众包任务邀请其他有关联的用户加入。移动用户完成感应数据的采集后上传感应数据到众包平台并获取众包人提供的报酬。众包人为了补偿用户完成众包任务的资源消耗，根据移动用户提交的感应数据贡献量计算报酬。同时，众包人为了激励移动用户以WoM模式感知众包任务，分别对市场中扩散任务邀请的移动用户和积极响应任务邀请的移动用户提供奖励。市场中，每个移动用户维护一个邀请列表用以记录其成功邀请到的移动用户，在提交感应数据到众包平台时一并提交邀请列表，众包人核实邀请列表并计算相应的报酬。WoM模式市场中的移动用户按邀请的时间顺序做出感应数据贡献量的决策，且邀请者用户与被邀请者用户的决策会直接影响彼此收益，市场中每一个用户都需考虑做出最佳的感应数据贡献量以最大化自身收益。市场中移动用户间就感应数据贡献量发生博弈行为，且用户的决策存在先后顺序，本文应用斯塔克伯格博弈模型分析移动用户间博弈行为，研究众包人与移动用户的最佳策略，为众包人制定众包任务及报酬评估提供参考依据。

本文针对WoM模式移动众包中的用户交互问题展开分析，主要工作如下。

1) 分析基于WoM模式移动众包市场中的用户交互过程，对市场中的移动用户进行分类定义。

2) 设计了移动用户的效应函数，根据用户贡献的不同计算相应的报酬，激励用户参与众包任务。

3) 建立了用户博弈的斯塔克伯格模型，基于逆向归纳法对博弈过程进行分析，证明了斯塔克伯格博弈均衡的存在唯一性，为众包人预测用户贡献并制定众包任务提供有效的参考。

4) 通过数值仿真实验验证了斯塔克伯格均衡的存在唯一性，探索了相关参数对效应函数以及均衡的影响。实验结果表明WoM模式任务感知和任务邀请提高了用户的参与度和众包任务的完成质量。

2 相关工作

移动众包相关技术已有广泛研究，主要包括移动众包市场的构建、单个众包方的任务分配、单个众包方激励机制设计、安全与隐私保护和移动众包市场演化机理研究等，本文研究WoM模式下单个众包方的任务分配及其市场演化。单个众包方的任务分配需要考虑众包人、众包任务和移动用户的特定需求，如众包人的预算限制或服务质量要求，众包任务的位置约束或时效性，以及移动用户的移动性等。

文献[6]针对众包人有预算限制提出基于代理的预算分配算法CrowdBudget，在不同的众包任务中划分出预算，基于真实的数据实验表明该算法与现有的算法相比降低了40%的估计误差。但是，该算法不适用于非二元任务分类，代理人无法辨识具有分发任务能力的用户。针对具有服务质量要求的感应任务分配问题，文献[7]提出了混合贪心和蜂群算法，最小化市场成本和最大化市场收益,但该研究工作为了保证稳定的空间覆盖，只考虑市场中的定期参与人，忽视了机会性参与人，无法获取更多的感应数据且缩小了空间覆盖范围；文献[8]提出了一种基于和声搜索的元启发式分配算法，实现了最大化众包平台收益的目标。

文献[9-10]针对众包任务具有位置约束的分配问题进行研究，文献[9]提出一个两阶段的优化方法，包括采用隐匿位置的全局优化方法和采用精确位置的局部优化方法，实现高感应数据覆盖率和低成本消耗的目标。然而，为隐匿位置的用户分配任务时，该方法忽略了移动用户的可信度，导致获取的感应数据质量较低。文献[10]设计了具有局部约束的精确传感效应函数，最大限度地利用传感效应解决众包任务分配问题，进一步针对感知任务分配的问题提出一种基于粒子群优化的最优算法。Chen等[11]研究了具有位置依赖的任务分配问题，考虑众包任务的地理特性和移动用户时空限制性，设计了高效的近似算法LRBA和基于讨价还价理论的定价机制。近似算法LRBA将任务分配问题分解成若干子问题，在单次迭代过程中重塑收益函数，该算法具有良好的可执行性，定价机制考虑了行为成本和市场需求。

文献[12-14]对众包任务具有时效性限制的任务分配问题进行研究。文献[12]提出高效、可信并满足个体理性的机制，为众包人招募合适的移动用户并支付合理的报酬提供了依据。文献[13]以非合作博弈模型分析异质用户间的行为交互，提出一种分布式任务选择算法，为移动用户计算任务选择并制定移动性方案，该文献的分布式任务选择算法是基于固定移动用户集，没有考虑用户群的动态变化。文献[14]提出了一种最小化任务总执行时间的近似算法，将近似最优比定义为算法执行时间与最优值的比值，该算法在不同的参数设置下具有良好的近似最优比。Zhang等[15]考虑任务多样性和任务依赖的用户可靠性因素，为异构众包市场的任务分配问题提出上下文相关的bandit规划方法。bandit方法中任务分配过程分阶段进行，在确定用户的可靠性并初始化权值后对用户进行选择。该方法试图最大化众包人在有限预算下的收益，从众包人的单一角度分析任务的分配问题，忽视了用户的收益情况。文献[16]研究了异构空间众包任务分配问题，建立了一种与分配过程相匹配的用户迁移行为预测模型，提出了有效的启发式方法，其中包括多轮线性权值优化和增强多目标粒子群优化算法，实现了众包任务的局部最优分配。

移动众包市场演化机理研究主要考虑市场中众包人和移动用户两两组合之间的竞争问题。Yang等[17]研究了在众包人报酬确定的情况下，移动用户决定工作量使收益最大化的问题，并用一轮斯塔克伯格博弈分析众包人与移动用户之间的竞争过程。单轮的静态模型虽有研究意义但多轮的动态模型更符合移动众包市场的运作。Peng等[18]基于多轮动态模型研究移动众包市场中的双边竞争问题，以非合作博弈模型对众包人之间竞争进行建模，以演化博弈模型对移动用户间竞争进行建模，分析得到博弈的稳定状态纳什均衡，并验证了均衡的收敛性。在移动用户的演化博弈中，用户对众包人的选择进行竞争演化，由于该文献是基于单一的DM模式众包市场，忽视了移动用户之间对感应数据贡献量的竞争。Sun等[19]对移动用户在一个众包方有多个感知过程情况下的感知行为进行研究，提出感应过程参与博弈的框架并基于拥塞博弈模型进行分析，设计出分布式算法求解参与人的最佳对策，并验证了系统的纳什均衡。Dong等[20]在多众包人的众包场景下，以非合作博弈模型建模用户间对众包人选择的竞争并用精英策略动力学求得博弈均衡结果。

综上所述，目前针对单个众包方的任务分配和移动众包市场演化机理的问题已有广泛研究，各种文献从不同的角度解决问题。但已有研究均基于单一的DM模式移动众包市场，忽略了WoM模式对市场的有利影响。WoM模式在建立众包用户群上具有高效性，并且能够依赖不同的网络通信方式实现用户邀请，以满足不同的众包任务要求。与现有研究工作不同的是，本文研究混合DM模式和WoM模式的移动众包市场中单个众包方的任务分配和市场演化机理问题，分析移动众包市场中WoM模式下的用户交互行为和邀请机制，设计移动用户的效应函数，基于斯塔克伯格博弈模型研究移动用户间博弈行为。

3 WoM模式下的移动众包市场框架

3.1 WoM模式移动众包市场模型

一个WoM模式移动众包市场由若干众包人、众包平台和大量移动用户所构成。如图1所示。众包人负责众包任务的制定和报酬的设计，移动用户对众包任务进行感知、参与并向其他移动用户发送众包任务邀请，众包平台作为市场中的第三方保证平台上信息的公开性与真实性。

3.1.1 市场交互

WoM模式移动众包市场中众包人、众包平台和移动用户间的交互行为如下。

1) 众包人在众包平台上发布众包任务和报酬评估情况。

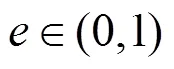
3) 移动用户感知众包任务,并维护自己的邀请列表，以便众包人对移动用户的贡献进行评估。参与众包任务的用户决定感应数据的贡献量并上传感应计划到众包平台。

4) 众包人从众包平台获取并记录移动用户的感应计划。

5) 移动用户按照感应计划完成众包任务并上传感应数据和邀请列表到众包平台。

6) 众包人通过众包平台获取感应数据和用户的邀请列表，核实邀请列表信息并计算用户的报酬。

7) 众包人支付用户报酬到众包平台，移动用户通过平台获取报酬。

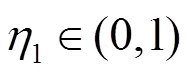
本文侧重于WoM模式下移动众包市场中移动用户行为的分析，考虑单个众包人、众包平台和若干移动用户的市场情形。

3.1.2 用户邀请机制

WoM模式是一种新颖的众包任务感知方式，移动用户通过其他移动用户的邀请感知众包任务。在移动众包市场中，众包人将众包任务发布到众包平台，成功感知的移动用户考虑是否向其他移动用户扩散众包任务邀请。被邀请的移动用户决定是否接受邀请并考虑是否继续扩散众包任务邀请，如此反复下去。在WoM模式移动众包市场中，成功感知众包任务的移动用户可以向外扩散任务邀请，因而在用户之间形成邀请与被邀请的关系。如图2所示，WoM模式移动众包市场的移动用户之间形成了类似森林结构的关系。本文根据移动用户间的邀请关系，将市场中的移动用户定义为4种级别。

零级移动用户：这种移动用户通过众包平台直接感知众包任务，与其他移动用户无关联，如图2中的移动用户1~3。

一级移动用户：这种移动用户以DM模式通过众包平台感知众包任务，以WoM 模式向外扩散任务邀请，如图2中的移动用户4~5。

二级移动用户：这种移动用户以WoM模式感知众包任务，即接受其他移动用户的任务邀请，并向外扩散任务邀请，如图2中的移动用户6~9。

三级移动用户：这种移动用户以WoM 模式感知众包任务，不向外扩散任务邀请，如图2中的移动用户10~13。

在移动众包市场中，任何参与了众包任务感知的移动用户一定属于上述4种级别移动用户中的某一种。

图1 一个WoM模式移动众包市场

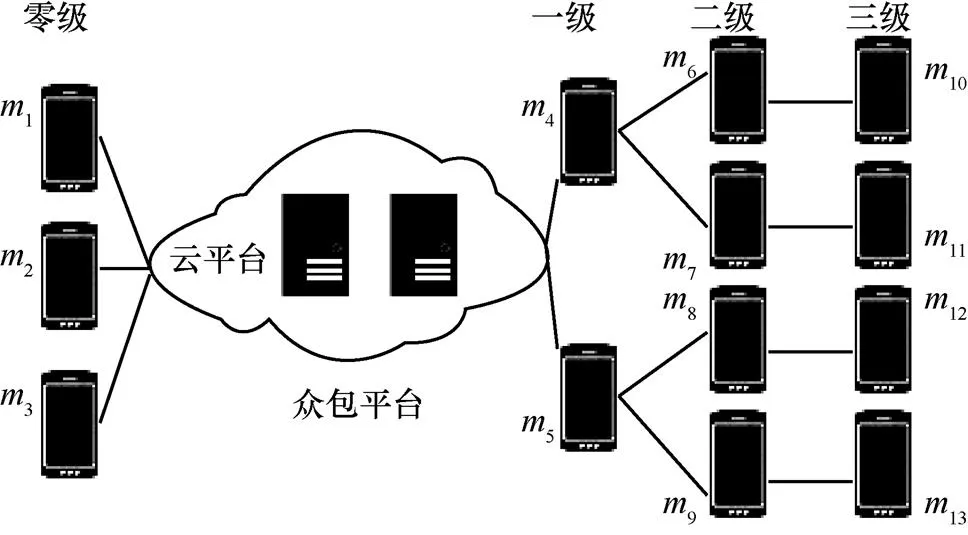
图2 WoM模式下移动用户的森林关系图

3.2 移动用户模型

3.2.1 用户行为

WoM模式移动众包市场中移动用户的行为如下。

移动用户感知众包任务，用户直接从众包平台或通过其他移动用户的邀请感知众包任务。

移动用户制定感应计划，确定感应数据贡献量。本文假设市场中的移动用户是完全理性的，移动用户基于自身收益最大化制定感应计划。因此，WoM模式移动众包市场中，一级、二级和三级移动用户在制定感应计划时需要考虑其邀请者和被邀请者的感应计划。

移动用户上传感应计划到众包平台，完成感应数据的收集后提交感应数据和邀请列表到平台。

移动用户从众包平台获取报酬。

图3 移动用户WoM模式任务感知和任务邀请

3.2.2 用户效应

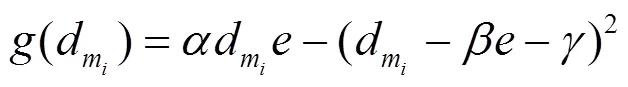
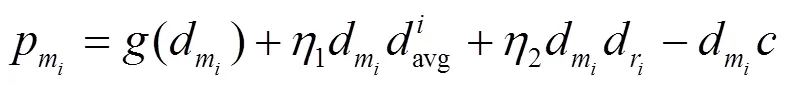
4 移动用户的博弈分析

本文基于博弈论研究WoM模式移动众包市场中移动用户间的行为交互，分析并预测市场中移动用户的贡献，预测结果为众包人设定众包任务和预算评估提供参考。在本文所描述的众包服务中，移动用户提交感应数据量的多少由移动用户自身决策，由于移动用户之间存在邀请与被邀请的关系，所以这一决策存在先后关系，且邀请者的决策直接影响被邀请者的决策。上述的用户交互特点与斯塔克伯格博弈模型特征相适应，所以本文基于斯塔克伯格模型对WoM模式下移动用户间的行为交互展开分析。

4.1 移动用户博弈的斯塔克伯格模型

WoM 模式下的移动用户行为交互问题可以建模成两阶段的斯塔克伯格博弈模型，这是一个由两博弈方组成的完全信息博弈模型，其中，一博弈方作为领导者，另一方是追随者[20]，第一个阶段是领导者做出决策的过程，第二个阶段是追随者做出决策的过程。在WoM模式下，邀请者作为斯塔克伯格模型的领导者，先做决策；被邀请者作为一个整体为追随者，后做决策。在WoM模式的移动众包市场中，移动用户间决策的先后顺序由加入到众包任务的时间顺序决定。本文采用逆向归纳法分析两阶段的斯塔克伯格博弈，首先分析第二个阶段追随者的决策过程，得到追随者的最佳对策；然后，根据第二阶段的结果反推出第一阶段博弈的最佳对策。假设在博弈中参与人均是完全理性且自私的，参与人只考虑最大化自身收益。在WoM模式移动众包市场中，由于邀请者无法知晓其被邀请者的后续行为，所以博弈只存在于邀请者与其直接被邀请者间。

图4 WoM模式三级用户关系

接下来，本文分别针对一级博弈和二级博弈展开建模分析。

1) 一级博弈

参与人的效应函数：领导者m的收益函数为

2) 二级博弈

参与人的效应函数：领导者m的收益函数为

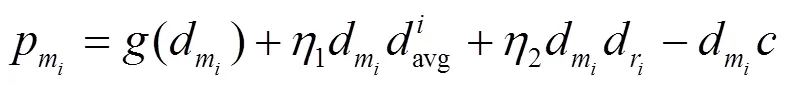
4.2 斯塔克伯格均衡

本文针对以上建模的一级博弈和二级博弈分别展开分析，探索博弈是否存在唯一的斯塔克伯格均衡。

1) 一级博弈分析

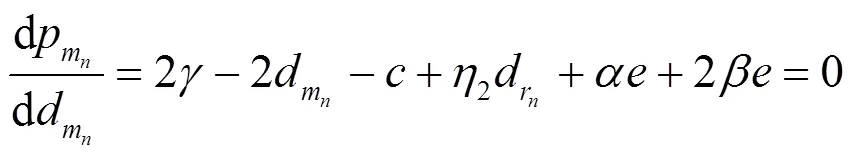
2) 二级博弈分析

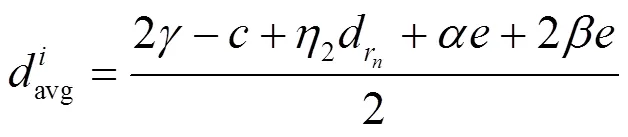
情况1 领导者设定其邀请者属于一级用户，有

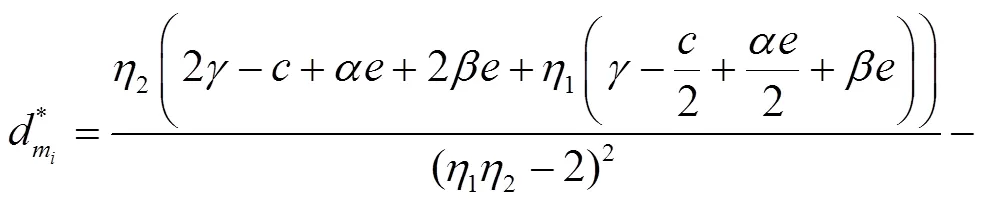
情况2 领导者设定其邀请者属于二级用户，有

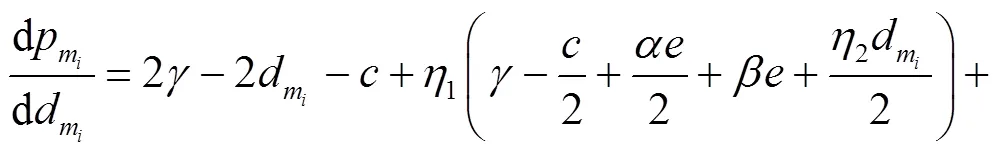
4.3 斯塔克伯格均衡的存在唯一性

本节将证明上述一级博弈和二级博弈中斯塔克伯格均衡的存在唯一性。在本文所讨论的斯塔克伯格博弈中参与人有领导者和追随者，本文分别对每个参与人的最佳对策进行证明。在这里以一级博弈过程为例证明，二级博弈的均衡证明可同理。

定理1 斯塔克伯格均衡存在且唯一

证明 首先，本文证明斯塔克伯格博弈中参与人的最佳对策唯一。

令上述一阶导数为0，可求得

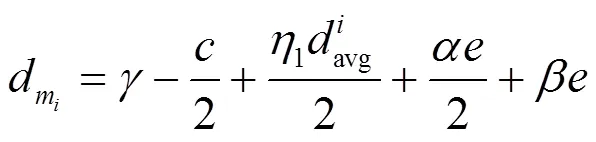
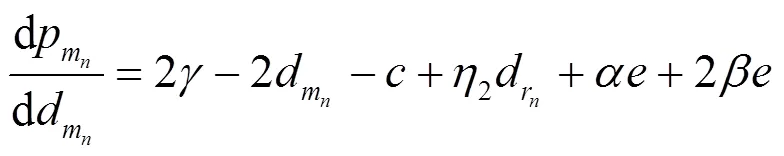
令上述一阶导数为0，可求得

斯塔克伯格均衡是斯塔克伯格博弈中每个参与人的最佳对策组合，如前所述，斯塔克伯格博弈中领导者和参与者都有唯一的最佳对策。因此斯塔克伯格均衡存在且唯一。证毕。

4.4 移动用户均衡算法

基于上述分析，本文提出计算斯塔克伯格均衡的算法，如算法1所示。

算法1 计算斯塔克伯格均衡算法

10) else

13) else

15) end if

16) end if

17) else:

19) end if

20) end for

5 仿真实验

5.1 仿真环境

表1 仿真参数设置

5.2 移动用户的最佳对策

图5 零级用户效应函数

图6 一级用户效应函数

图7 二级用户效应函数

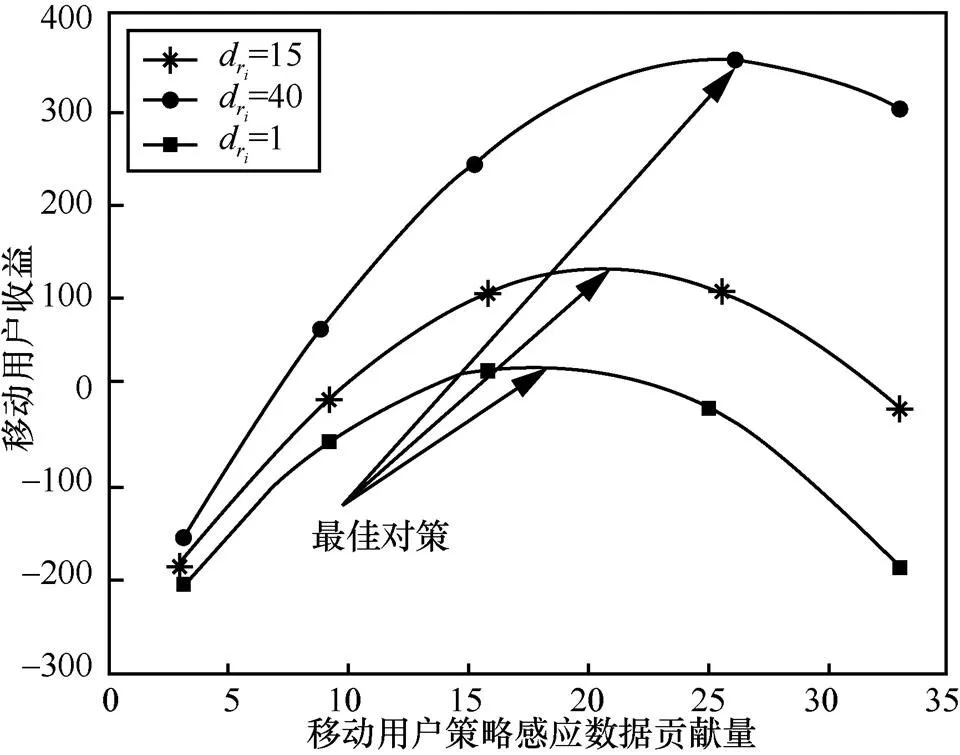
图8 三级用户效应函数

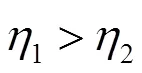
综上所述，WoM模式的任务感知和邀请行为为用户带来更高的效应且提高了用户的任务完成质量，因此用户将倾向于进行WoM模式的任务感知和用户邀请。

5.3 斯塔克伯格均衡的唯一性

本文以斯塔克伯格模型将WoM模式市场中的移动用户间交互建模成一级博弈和二级博弈。上文分别研究了一级博弈和二级博弈中均会存在着唯一确定的斯塔克伯格均衡。这里给出了一级和二级博弈中领导者和追随者最佳对策的曲线，根据斯塔克伯格均衡的几何意义，在领导者和追随者各自最佳对策曲线的交点处取得斯塔克伯格均衡。

图9展现了一级博弈的斯塔克伯格均衡。二级博弈要考虑领导者的邀请者类别，图10描述了领导者设定其邀请者进行DM模式任务感知时的斯塔克伯格均衡，图11描述了领导者设定其邀请者进行WoM模式任务感知时的斯塔克伯格均衡。对比这几种不同的斯塔克伯格均衡发现二级博弈中领导者在均衡处取得的策略（数据贡献量）明显大于一级斯塔克伯格博弈。这是因为一级博弈中领导者是以DM模式感知众包任务，而二级博弈中领导者是以WoM 模式感知众包任务，不同的感知方式导致用户所获得的收益不同，不同程度上激励用户做出感应数据量的决策。

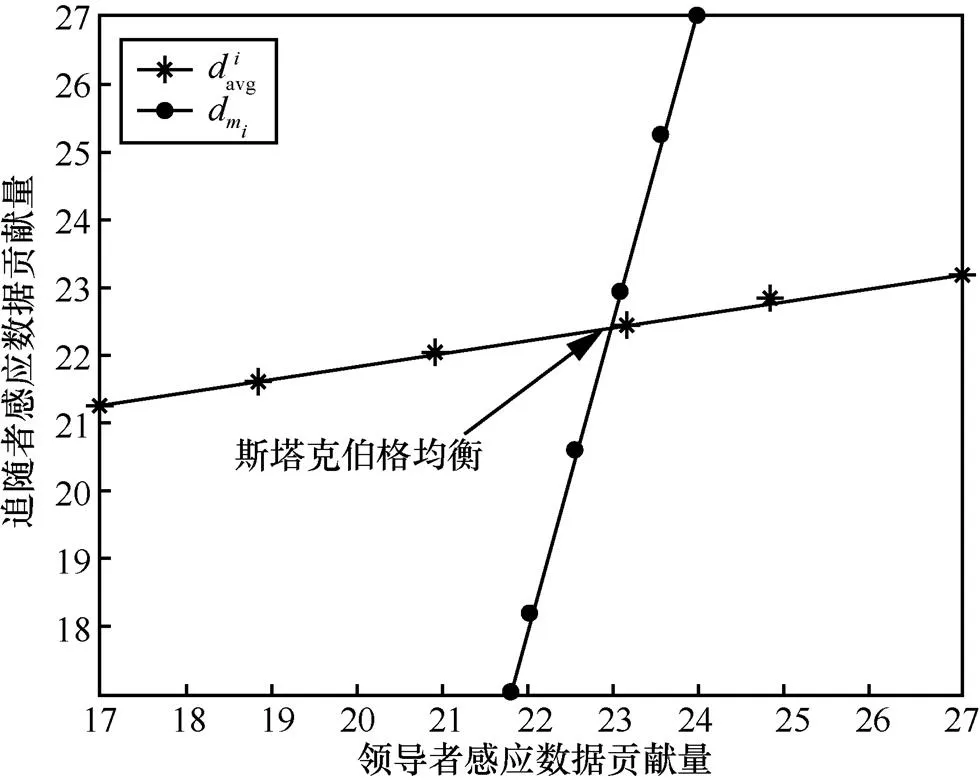
图9 一级博弈的斯塔克伯格均衡

图10 二级博弈的斯塔克伯格均衡情况1

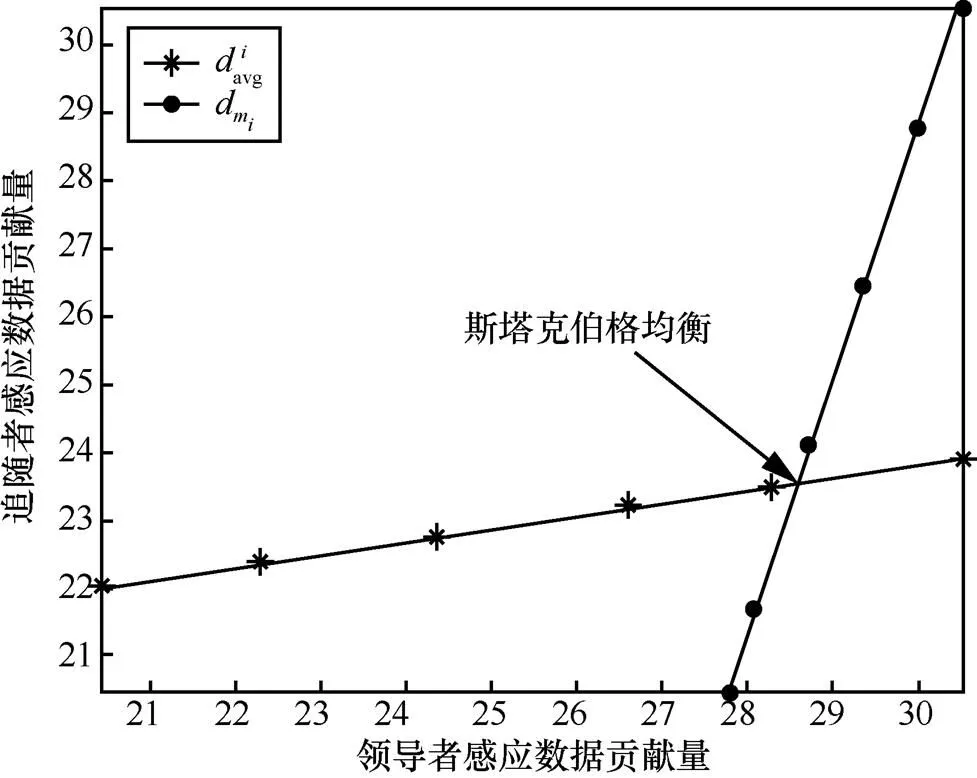
图11 二级博弈的斯塔克伯格均衡情况2

5.4 任务推荐值对用户效应和最佳对策的影响

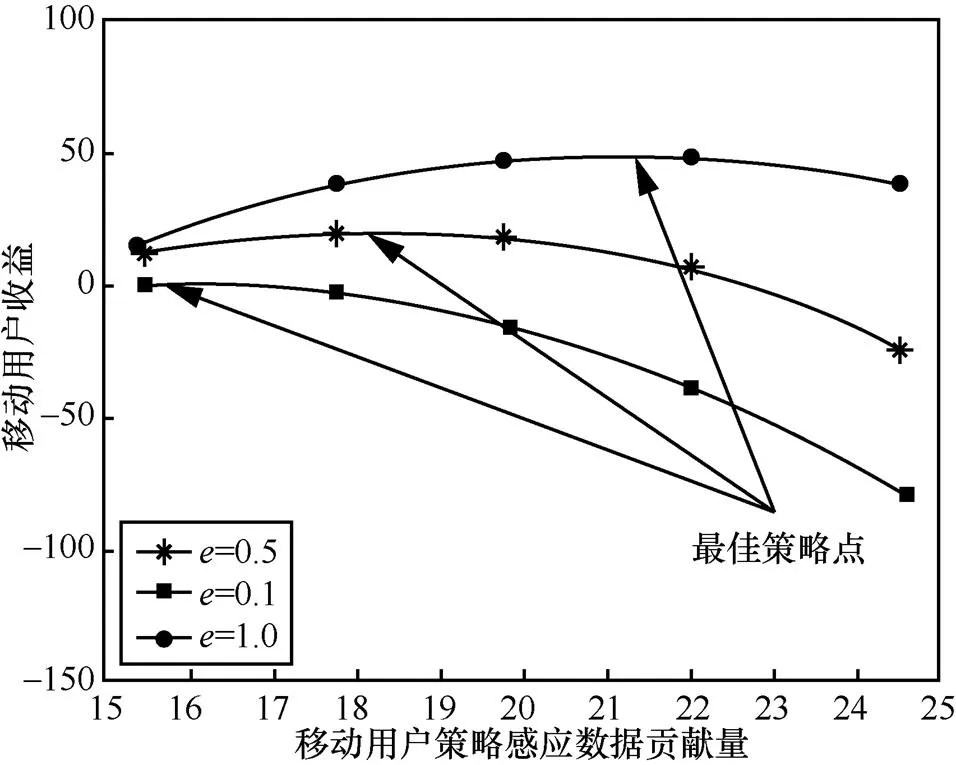
图12 任务推荐值对零级用户效应函数和最佳策略的影响

图13 任务推荐值对一级用户效应函数和最佳对策的影响

图14 任务推荐值对二级用户效应函数和最佳对策的影响

图15 任务推荐值对三级用户效应函数和最佳对策的影响

5.5 回报率、对斯塔克伯格均衡的影响

图16 回报率和对一级博弈斯塔克伯格均衡的影响

图17 回报率和对二级博弈斯塔克伯格均衡的影响情况1

图18 回报率和对二级博弈斯塔克伯格均衡的影响情况2

这种实验现象的出现是合理的，这是由于回报率的增加或减小会直接影响与WoM模式相关移动用户的效应，众包人给予的回报率越大可以更好地激励WoM模式相关移动用户做出高质量的数据感应。

6 结束语

本文针对WoM模式移动众包市场中移动用户的行为交互问题进行分析并以斯塔克伯格博弈模型建模，用逆向归纳法分析博弈过程得到唯一确定的斯塔克伯格均衡。通过仿真实验评估了移动用户的效应函数性能，验证了斯塔克伯格均衡的存在唯一性，并讨论了相关参数对斯塔克伯格均衡的影响。市场中，众包人通过对移动用户的交互行为进行博弈建模预测用户的感应数据贡献量并评估报酬范围，这为众包人制定众包任务提供理论支持，对WoM模式移动众包市场运行具有重要意义。

接下来的工作将考虑从众包人的角度分析WoM模式移动众包市场中的博弈问题，设计出有关激励机制进一步促进移动用户以WoM模式进行众包任务感知，提高移动用户参与度。

[1] PENG J, ZHU Y, SHU W, et al. Behavior dynamics of multiple crowdsourcers in mobile crowdsourcing market[J]. IEEE Network the Magazine of Global Internetworking, 2016, 30(6):92-96.

[2] LI H, OTA K, DONG M, et al. Mobile crowdsensing in software defined opportunistic networks[J]. IEEE Communications Magazine, 2017, 55(6):140-145.

[3] LANE N D, MILUZZO E, LU H, et al. A survey of mobile phone sensing[J]. IEEE Communications Magazine, 2010, 48(9):140-150.

[4] KHAN W Z, XIANG Y, AALSALEM M Y, et al. Mobile phone sensing systems: a survey[J]. IEEE Communications Surveys & Tutorials, 2013, 15(1): 402-427.

[5] WANG Y, JIA X, JIN Q, et al. Mobile crowdsourcing: framework, challenges, and solutions[J]. Concurrency & Computation Practice & Experience, 2017, 29(3):1-17.

[6] TRAN-THANH L, VENANZI M, ROGERS A, et al. Efficient budget allocation with accuracy guarantees for crowdsourcing classification tasks[C]//International Conference on Autonomous Agents and Multi-Agent Systems. 2013:901-908.

[7] WANG Z, HUANG D, WU H, et al. QoS-constrained sensing task assignment for mobile crowd sensing[C]//IEEE Global Communications Conference (GLOBECOM’14). IEEE, 2014:311-316.

[8] AMIN R G, LI J, ZHU Y. A new harmony search based allocation algorithm for location dependent tasks in crowdsensing[C]// International Conference on Progress in Informatics and Computing. 2016: 581-585.

[9] POURNAJAF L, XIONG L, SUNDERAM V, et al. Spatial task assignment for crowd sensing with cloaked locations[C]//Proceedings of International Conference on Mobile Data Management. IEEE, 2014: 73-82.

[10] ZHAI L, WANG H. Crowdsensing task assignment based on particle swarm optimization in cognitive radio networks[J]. Wireless Communications and Mobile Computing, 2017:1-9.

[11] HE S, SHIN D H, ZHANG J, et al. Near-optimal allocation algorithms for location-dependent tasks in crowdsensing[J]. IEEE Transactions on Vehicular Technology, 2017, PP(99):3392-3405.

[12] MINDER P, SEUKEN S, BERNSTEIN A, et al. CrowdManager - combinatorial allocation and pricing of crowdsourcing tasks with time constraints[C]//ACM Conference on Electronic Commerce. ACM, 2012: 1-18.

[13] MAN H C, SOUTHWELL R, HOU F, et al. Distributed time-sensitive task selection in mobile crowdsensing[C]//The ACM International Symposium on Mobile Ad Hoc Networking and Computing. ACM, 2015:157-166.

[14] WU X, HUANG D, SUN Y E, et al. An efficient allocation mechanism for crowdsourcing tasks with minimum execution time[C]//International Conference on Intelligent Computing . 2017:156-167.

[15] ZHANG H, MA Y, SUGIYAMA M. Bandit-based task assignment for heterogeneous crowdsourcing[J]. Neural Computation, 2015, 27(11): 2447-2475.

[16] WANG L, YU Z, HAN Q, et al. Multi-objective optimization based allocation of heterogeneous spatial crowdsourcing tasks[J]. IEEE Transactions on Mobile Computing, 2017, PP(99):1637-1650.

[17] YANG D, XUE G, FANG X, et al. Crowdsourcing to smartphones: incentive mechanism design for mobile phone sensing[C]//Annual International Conference on Mobile Computing and Networking. 2012:173-184.

[18] PENG J, ZHU Y, SHU W, et al. When data contributors meet multiple crowdsourcers: Bilateral competition in mobile crowdsourcing[J]. Computer Networks, 2016, 95(11):1-14.

[19] SUN Y, ZHU Y, FENG Z, et al. Sensing processes participation game of smartphones in participatory sensing systems[C]//Annual IEEE International Conference on Sensing, Communication, and Networking. IEEE, 2014: 239-247.

[20] DONG X, ZHANG X, YI Z, et al. Incentive mechanism for crowdsensing platforms based on multi-leader stackelberg game[C]// International Conference on Communicatins and Networking. 2016: 138-147.

[21] WENNERSTROM H, SMITH D B. A game theoretic approach to sensor data communications in an opportunistic network[C]// International Conference on Communications. 2015:6306-6311.

[22] PENG J, WU M Y, ZHU Y, et al. How multiple crowdsourcers compete for smartphone contributions[C]//IEEE Conference on Computer Communications. IEEE, 2015:516-521.

Game-theoretical analysis of mobile contributors in mobile crowd sourcing network with word of mouth mode

ZENG Feng1, WANG Runhua1, PENG Jia2, CHEN Zhigang1

1. School of Computer Science and Engineering, Central South University, Changsha 410000, China 2.State Key Laboratory of Air Traffic Management System and Technology, Nanjing 210000, China

The crowdsourcer who calls for sensing service can recruit enough mobile contributors quickly with the word of mouth mode, improving the quality of sensing tasks. The behavior of mobile contributors in mobile crowdsourcing with the WoM was investigated. It was supposed that each mobile contributor was rational, seeking for the highest utility. The behavior of mobile contributors with a two-level Stackelberg game was formulated. In the first-level game, a mobile contributor who directly worked for the crowdsourcer acted as the leader, while contributors invited by first-level contributors were followers called the second-level contributors. In the second-level game, the second-level contributors were the leaders and contributors invited by them were followers. The Nash equilibrium for each Stackelberg game was proved was existed and unique, and designed an algorithm to reach the equilibrium. Backward induction approach to compute the best response of each game was adopted, and the simulation results show the correctness of theoretical analysis for the interaction among contributors in crowdsoucing with WoM.

mobile crowdsourcing, word of mouth mode, game theory, Stackelberg game

TP309

A

10.11959/j.issn.1000−436x.2019029

2018−07−11；

2018−12−29

国家自然科学基金资助项目（No.61672540, No.61502159）

The National Natural Science Foundation of China (No.61672540, No.61502159)

曾锋（1977− ），男，广东梅州人，博士，中南大学副教授，主要研究方向为边缘计算、群智感知网络、车联网与人工智能等。

王润华（1996− ），女，安徽安庆人，中南大学硕士生，主要研究方向为移动众包网络、群智感知网络与博弈论等。

彭佳（1990− ），女，土家族，湖南张家界人，博士，空中交通管理系统与技术国家重点实验室工程师，主要研究方向为群智感知网络、博弈论与机制设计、智能交通与空中交通网络优化等。

陈志刚（1964− ），男，湖南益阳人，博士，中南大学教授、博士生导师，主要研究方向为计算机网络及分布式计算。