基于集对分析法的水利工程安全人因分析

，，，，

(1.三峡大学水利与环境学院，湖北宜昌443000；2. 武汉市汉阳市政建设集团有限公司，湖北武汉430000；3. 贵州省水投水务集团有限公司，贵州贵阳550002；4. 福建省水利水电工程局有限公司，福建泉州362000)

近年来，中国高度重视水利工程施工安全管理，加强了水利工程安全管理力度，但事故总起数与伤亡人数依旧偏高[1]。统计中国近10 a间的火灾、交通、煤矿等事故，得出人因事故占总事故发生率的88%[2]。这表明人的因素已成为诱发事故的最主要因素之一[3]。因此，基于人因因素开展水利工程安全评价，对科学认识水利工程安全水平、预防控制事故发生具有重要意义。

人因分析作为水利工程施工安全评价的重要内容，众多学者对此进行了深入研究。Jan K Wachter等[4]通过分析安全事故数据，强调了人对减少事故发生的重要性；Zheng等[5]建立HFACS模型揭示水利工程事故中人因致因机理；王岗等[6]通过研究水利工程施工作业过程中各因素与施工环境的联系，运用多级可拓理论构建了水利工程施工环境评价指标与安全等级的关联函数；孙志禹等[7]运用实证贝叶斯方法，研究了水利工程中人因事故引发的人员伤亡概率问题；孙开畅等[8]基于人因分析分类系统,识别水利工程高危作业人因因素，通过引入认知地图理论，识别和分析事故中的关键人因因素；宋四新等[1]提出适用于水电工程施工安全风险分析的HFACS模型，建立了结构方程模型分析事故涉及人因因素之间的影响程度；郑霞忠等[9]基于Euclid理论，从作业人员等4个方面建立了水利工程施工安全熵评价模型，分析水利工程施工安全水平。

上述研究从多个角度阐述了水利工程安全事故中的人因因素，对分析事故诱发机理具有重要意义，但在水利工程施工安全评价中，上述研究较少考虑评价过程中的模糊、随机、中介和信息不完全等这些不确定性因素。鉴于此，笔者同时考虑水利工程施工安全评价中的确定性和不确定性因素，采用集对分析法，同时在指标权重确定过程中引入区间数学理论建立客观的权重值，对水利工程施工安全现状水平及安全态势进行分析，以期为水利工程施工安全管理工作提供指导建议。

1 水利工程HFACS模型建立

HFACS模型是调查和分析安全事故中人因失误的系统性工具，其基于Reason的瑞士奶酪模型，将事故致因的多重因果性自下而上依次表示为组织影响、不安全行为的监督、不安全行为的前提和不安全行为4个层次，可以同时考虑到安全事故中的直接因素和潜在因素[10]。

针对水利工程施工的复杂性和危险性，根据文献分析[7-8]和现场调研，结合《企业施工安全标准化基本规范》等安全标准规范，综合考虑事故致因分析的合理性。应用HFACS模型分析事故中人因因素，根据水利工程施工安全管理、施工作业和技术措施等特点，对原框架进行修改，使其满足本行业法律法规和安全生产标准化体系。调整后的水利工程HFACS 模型共包括 5 类事故致因，23个人因因素，模型结构见图 1。

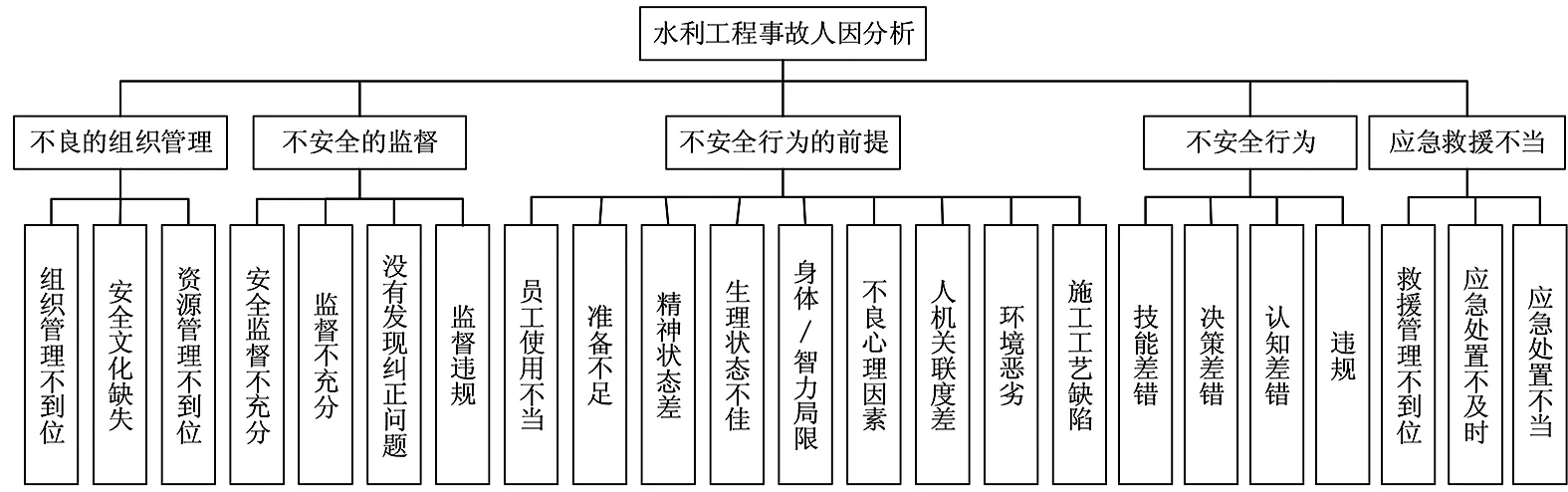
图1 改进后的水利工程事故HFACS模型

2 集对分析评价方法

2.1 集对分析法

安全评价方面集对分析法常被用来解决致因因素的确定性和不确定性问题[11-12]。集对分析法中把客观事物之间的联系视为一个确定不确定性的系统，通过2个相关集合构建集对，建立同、异、反联系度，对集对中元素特征的同一性、差异性、对立性进行分析[13-14]。依据水利工程人因分类系统模型建立的指标体系，将水利工程安全管理涉及到的人因因素评价标准分数记作集合X，实际得分记作集合Y，组成集对记作：H=(X,Y)，分解两集合间的联系，得到N项特性联系，S为两集合共有特征,P表示两集合相互对立的特征，将剩下的特性计作F，将水利工程施工评价中涉及到的指标间联系度表示为：

(1)

由于实际问题中研究对象的复杂性，联系度表达式通常根据具体问题会进行不同层次扩展，建立为一种多元联系数表达联系度公式，见式(2)：

(2)

式中wk——特征的权重。

2.2 集对势

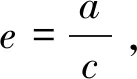
2.3 安全等级划分

根据均分原则，设置水利工程安全等级U={Uj,j=1,2,3}，见表2。

2.4 悲观势

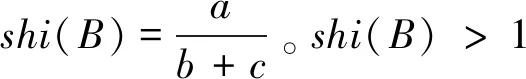
表1 集对势等级分析

表2 安全等级划分标准

3 指标综合权重的确立

在运用集对分析的过程中，指标权重确立的科学与否关系到评价结果的客观性。由于专家的自身经验及知识储备的差异性，会使得某些指标权重的确立存在不确定性；同时在传统的AHP法中会依据专家在专业领域中的威望确立专家权重，使得在决策过程中不能体现专家客观认识度[15]。为保证指标权重确立的客观性，考虑到区间数学理论在解释不确定性问题中的优势，在指标权重确立的过程中，运用区间数来建立区间判断矩阵，根据数据的差异性和相似性，确立专家置信度，进而根据相关公式计算得到指标的综合权重。基于区间数学理论计算指标权值的具体步骤如下。

a) 确定专家的置信度:

(3)

式中ri——第i位专家的置信度；λi、ηi——在进行归一化处理后，第i位专家和其他专家的评判结果间的相似性水平、差异性水平。

b) 确定指标主观权重：

(4)

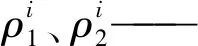
c) 确定指标客观权重：

(5)

式中ωt2——专家对第t项评价指标的客观权重；bdt——计算中间变量值；gt——专家主观权重值的ωt1可靠度。

d) 确定指标综合权重：

(6)

4 应用实例

以四川省内某水利工程为例，为评估该水利工程安全管理现状状况，结合本文建立的水利工程HFACS 模型涵盖 5 类事故致因，23 类人因因素，采用不确定型AHP法确立各个因素权值，应用集对分析理论评价该水利工程的安全管理现状。

4.1 指标赋权

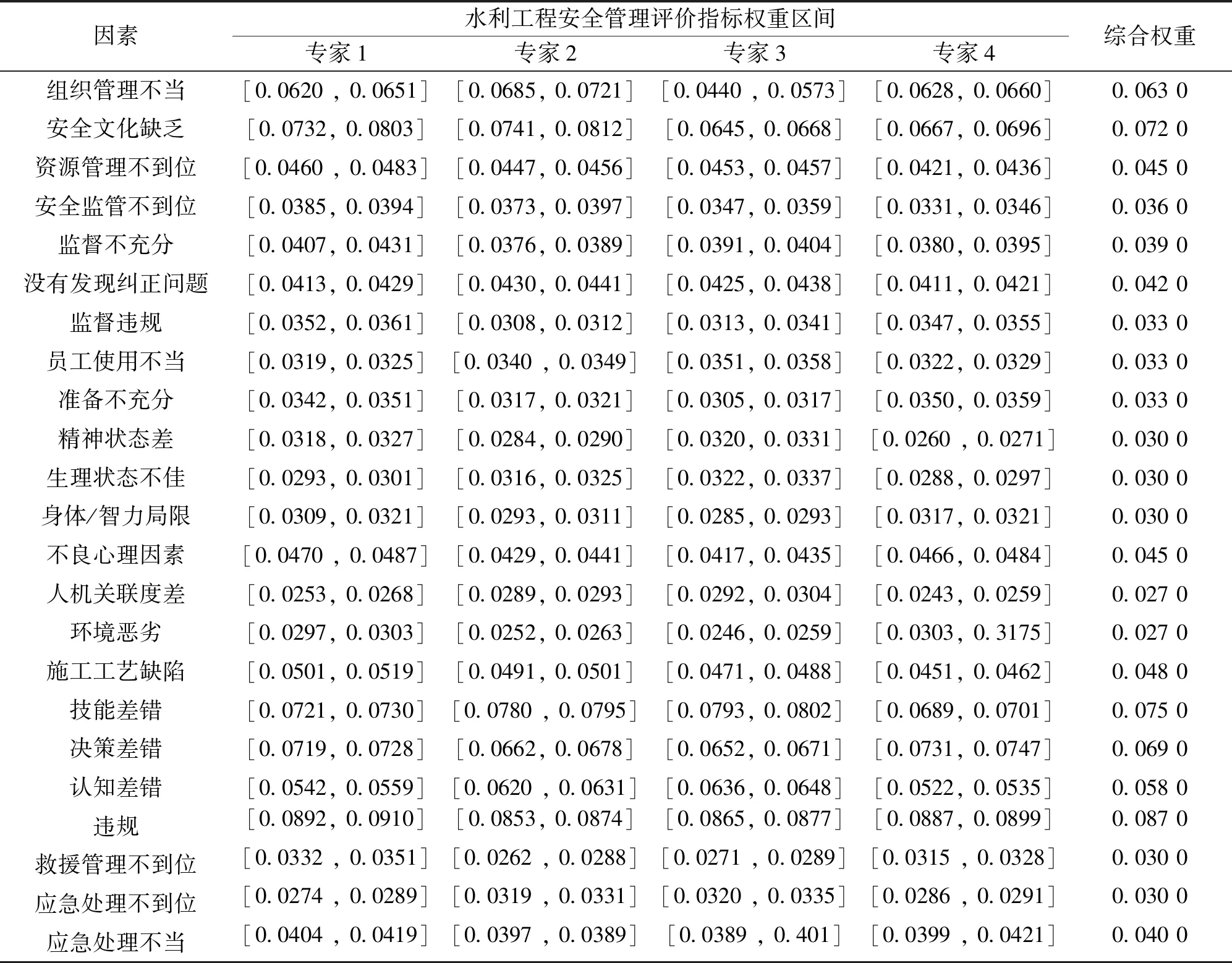
运用区间数学理论，由4位专家针对该水利工程23类指标权重值进行评判，4位专家的置信水平依次为0.253 1、0.247 3、0.249 5、0.250 1。根据式(3)—(6)计算指标的综合权重见表3。

计算各指标综合权重ωt=(0.063，0.072，0.045，0.036，0.039，0.042，0.033，0.033，0.033，0.030，0.030，0.030，0.045，0.027，0.027，0.048，0.075，0.069，0.058，0.087，0.030，0.030，0.040)

4.2 联系度计算

通过调查问卷的形式对该水利工程进行等级评定，根据集对分析模型中“同、异、反”3 种不同情况，对问卷中23 项指标设置“好”“一般”“差”3 个选项，向水利工程管理层、技术员、安全员、水利工程监管部门、参与工程建设的专家及验收人员发放了 100份问卷(表4)。

表4 各级指标问卷调查统计数据

运用 SPSS 软件对调查问卷数据进行信度检验，得到Cronbachα值为0.813，表明问卷数据具有可信度。归一化处理后得到矩阵R。

将ωt和R代入式(2)进行计算，得到水利工程事故人因联系度μ=0.653+0.251i+0.092j。

4.3 集对分析评价

a) 集对势分析。通过集对分析法计算得到该水利工程的同一度a=0.653，差异度b=0.251，对立度c=0.092。由表1可以看出，该水利工程集对势同一趋势为主，但同一趋势较弱，为弱同势。差异度b=0.251表明部分指标有变坏趋势，需要对表中部分指标进行调整。

b) 联系度分析。在联系度计算式中，当i=1时，此时μ=0.812，根据表2可知此时的安全状态为“好”，当i=-1时，此时μ=0.310,安全状态为“一般”。此水利工程联系度μ∈[0.310,0.812]，处于“一般”与“好”等级间，这表明该水利工程安全管理中的人因管理工作较好。

c) 悲观势分析。根据联系度表达式，在最不利情况下悲观势为1.903，表明该水利工程安全现状处于“安全”等级。

d) 不确定性分析。系统的不确定性由差异度决定，差异度b值与系统不确定性有同趋性，此水利工程差异度b=0.251。表明此水利工程的不确定性较高，虽从总体来看，安全状况较好，但仍需对某些人因因素及时排查整改。

5 结论

水利工程安全管理现状评价是工程安全管理中的重要环节，结合HFACS模型构建水利工程安全管理中的人因因素，应用集对分析理论将安全评价等级转化为同、异、反联系数，在水利工程安全管理现状评价的过程中，可以较好考虑水利工程安全管理系统的确定和不确定性问题，保证水利工程施工安全评价结果的客观真实。

运用集对分析中集对势、联系度、不确定性和悲观势对评价进行定量分析，解决了HFACS 模型只能定性分析问题的局限，不仅更加客观地从整体上把握水利工程人因安全现状，还可以分析安全管理的未来趋势，弥补了确定性评价结果的单一性。