基于网络分析法的通用装备维修合同商保障能力评估

王 谦，程中华，白永生，马全跃，宋 星

(1.陆军工程大学石家庄校区， 石家庄 050003； 2.陆军第九综合训练基地， 河北 张家口 075000)

通用装备是我军装备体系中极为重要的一部分，配备数量大、分布范围广、使用率高。通用装备维修保障作为军队装备发展建设过程中的一个环节，也具有十分重要的地位。在和平时期，装备维修保障对于提高装备完好率、使用率发挥着相当大的作用。在战争时期，装备维修保障更是能够为部队顺利使用装备、更好地发挥装备作战效用具有决定性的影响。军民融合企业在我国国家安全和经济发展中占有重要地位，而装备性能的充分发挥需要维修保障工作的支持。当前，随着通用装备配备的数量以及装备使用率的增加，其维修保障费用也随之提高，部队在装备维修保障方面的负担也不断加重。缓解通用维修保障任务重与现有部队维修保障力量不足、维修保障经费不断增加与经费有限之间的矛盾，走军民融合的发展道路成为提高装备维修保障能力的必然选择。

借鉴国外维修保障实践经验，结合我军通用装备维修保障的实际情况，将通用装备军民融合维修保障分为3种形式：合同商辅助性保障、完全外包型保障和军地联合保障[1]。在合同商选择中，由于部队无法全面准确地衡量合同商的各项信息，通常就是通过检查资质并进行招标来选择合同商。在大力推进军民融合式维修保障建设的进程中，合同商参与通用装备维修保障可能会给军方带来风险[2]。因此，如何选择最佳合同商，对更好地完成通用装备军民融合维修保障具有决定性的作用。本文对影响军民融合企业装备维修保障能力的指标要素进行选取和分析，构建了基于网络分析法(Analytic Network Process，ANP)的通用装备维修合同商保障能力影响因素评价模型，为合同商保障能力的提高提供参考建议[3]。

1 ANP典型结构及超矩阵算法

网络分析法(ANP)[4]，是对层次分析法(AHP)的进一步拓展[5]。该方法将以往对层次结构的决策指标体系扩展为对网络结构决策指标体系研究，解决不同层次间元素的相互影响问题。将ANP引入到通用装备维修合同商保障能力影响因素研究分析中，综合考虑各层次因素间的相互影响和反馈性。通过计算极限超矩阵确定各影响因素的排序并得到综合权重，可以作为确定通用装备维修合同商保障能力影响因素的一种方法。

在ANP中，系统元素由控制层元素和网络层元素组成[6](其结构如图1)。控制层包括总目标及决策准则，网络层是由所有受控制层支配的元素组组成[7]。

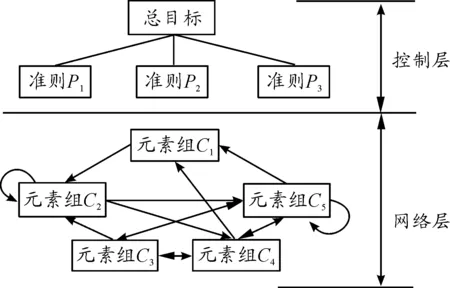
图1 ANP结构

基本步骤为：

1) 建立模型；

2) 计算超矩阵；

3) 计算极限超矩阵并确定权重和综合排序[8]。

2 基于ANP的通用装备维修合同商保障能力影响因素分析

2.1 建立影响因素指标体系

指标体系的建立，既要立足部队对装备维修保障的需求，还要考虑科学性、系统性、定性指标和定量指标相结合等一般原则。通过广泛查阅资料，对通用装备维修合同商保障能力的诸多因素进行系统理论分析[9]，并在征求相关领域权威专家意见的基础上，本文从合同商资质、发展潜力、技术能力、价格成本、管理水平等五个方面构建合同商保障能力因素指标体系[10]，如图2所示。

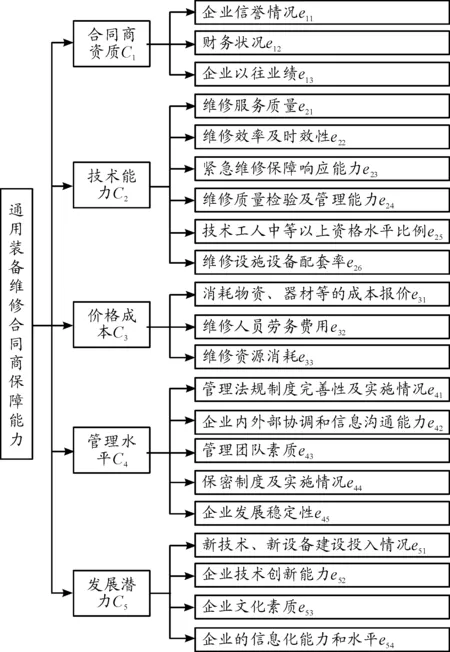
图2 通用装备维修合同商保障能力影响因素指标体系

在以往的研究中，人们通常将这些影响因素之间以相互独立的关系进行处理，但这并不符合实际情况。例如：由经验可知，维修人员劳务费用会影响到维修效率及时效性，新技术、新设备建设投入情况会影响维修服务质量，技术工人中等以上资格水平比例会影响企业的信息化能力和水平等等。通过分析，各因素之间有如表1所示的影响关系。

2.2 基于ANP的通用装备维修合同商保障能力影响因素网络模型

通过全面衡量各种因素之间影响关系，建立了ANP典型结构的通用装备维修合同商保障能力影响因素的网络模型，如图3所示。模型在控制层将通用装备维修合同商保障能力影响因素作为研究目标，网络层有五个指标集，每个指标集中均有二级指标(共21个)。单、双箭头分别表示指标之间存在影响关系和互相反馈关系。

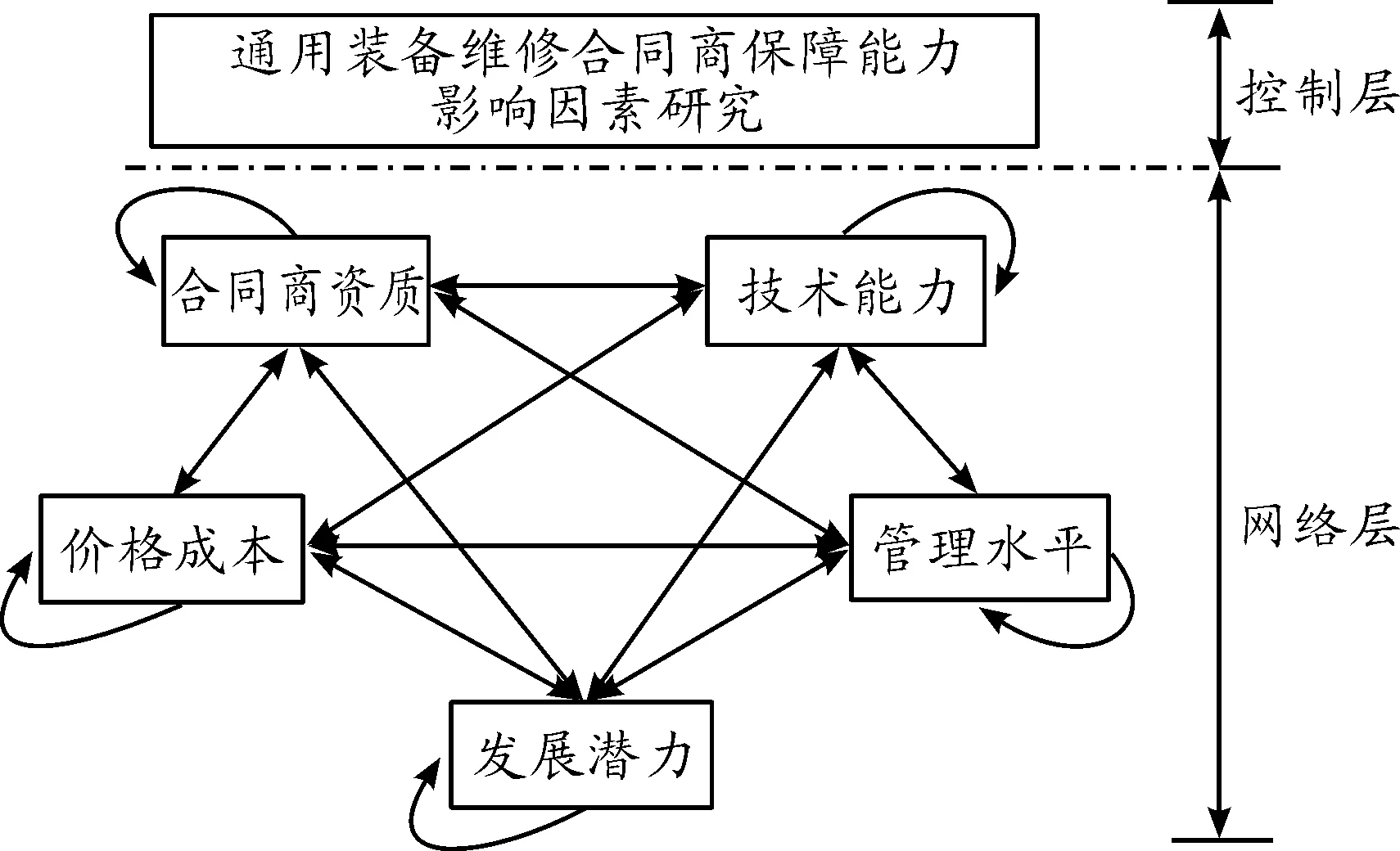
图3 通用装备维修合同商保障能力影响因素ANP指标体系网络模型

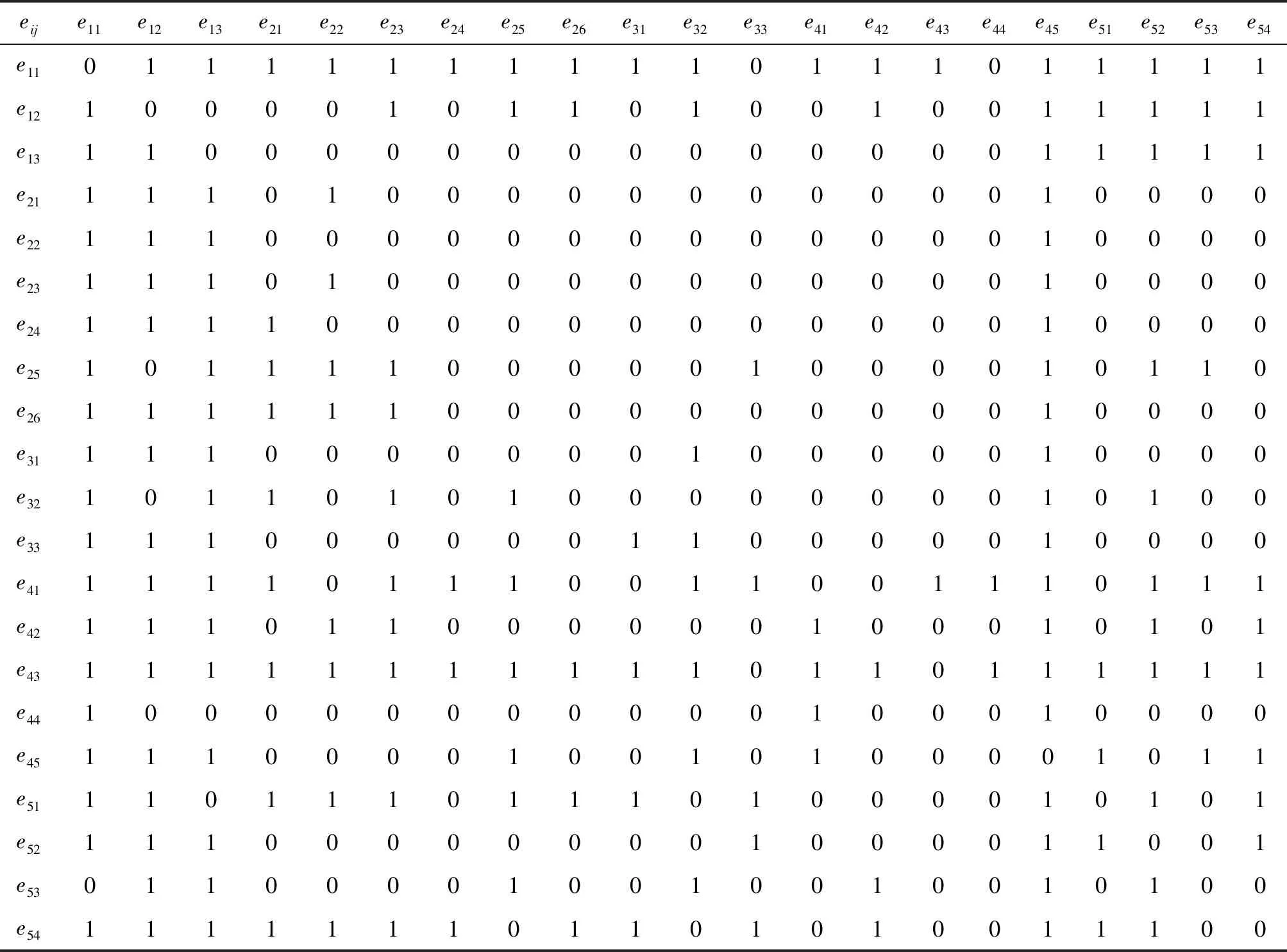
表1 网络结构中的因素影响关系

注：1表示有影响，0表示无影响。

2.3 计算通用装备维修合同商保障能力影响因素指标的综合权重

在对ANP模型计算时，极限超矩阵等计算过程非常复杂，通过人工计算较难完成。本文利用Satty等推出的超级决策软件Super Decision(SD)，进行程序化的ANP计算。

1) 对各指标之间重要程度进行比较分析

在分析通用装备维修合同商保障能力影响因素这一目标下，根据已经建立的ANP网络模型，通过征询相关领域权威专家的意见，构造判断矩阵。图4给出了以价格成本为标准的一级因素指标之间重要程度。图5表示判断矩阵的一致性检验结果为0.092 63，低于0.1，此结果可接受。图6给出了合同商资质C1中元素按其对企业发展稳定性e45的影响力大小而进行的二级指标优势度。按同样的方法进行比较，文中不进行一一列出。

2) 计算未加权超矩阵和加权超矩阵

通过利用超级决策软件Super Decision进行计算。表2为发展潜力C5指标集中各指标之间影响程度得到的未加权超矩阵中各元素值，表3为发展潜力C5指标集中各指标之间影响程度得到的加权超矩阵中各元素值。由于篇幅所限，不一一列举。

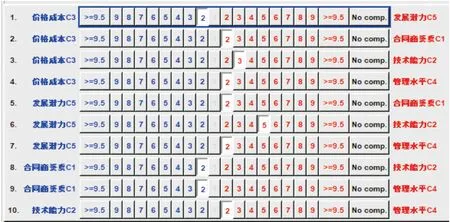
图4 以价格成本为标准的一级因素指标之间的重要程度

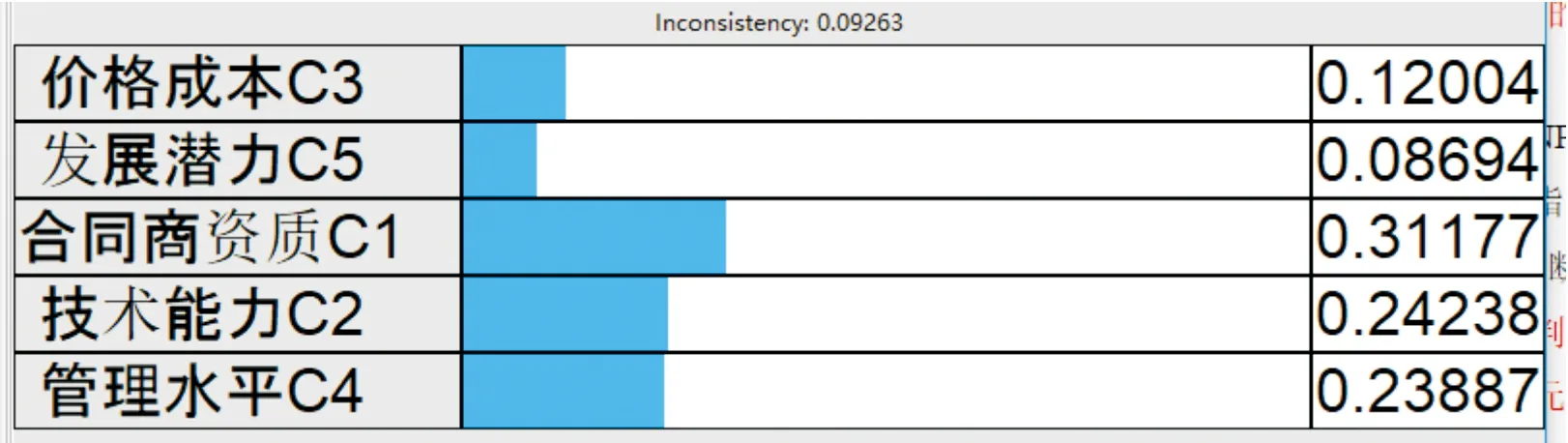
图5 一级因素指标比较判断矩阵的一致性检验

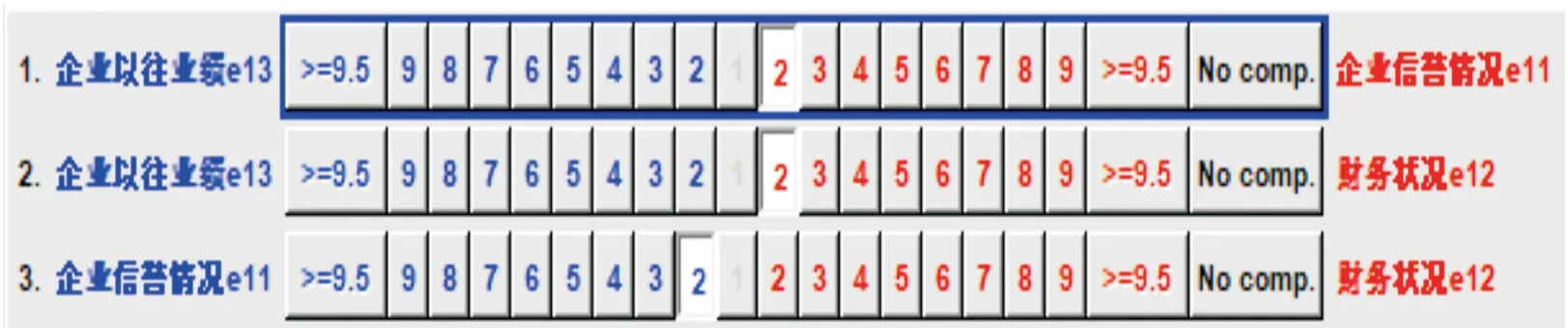
图6 合同商资质C1中元素按其对企业发展稳定性e45的影响力大小的二级指标优势度

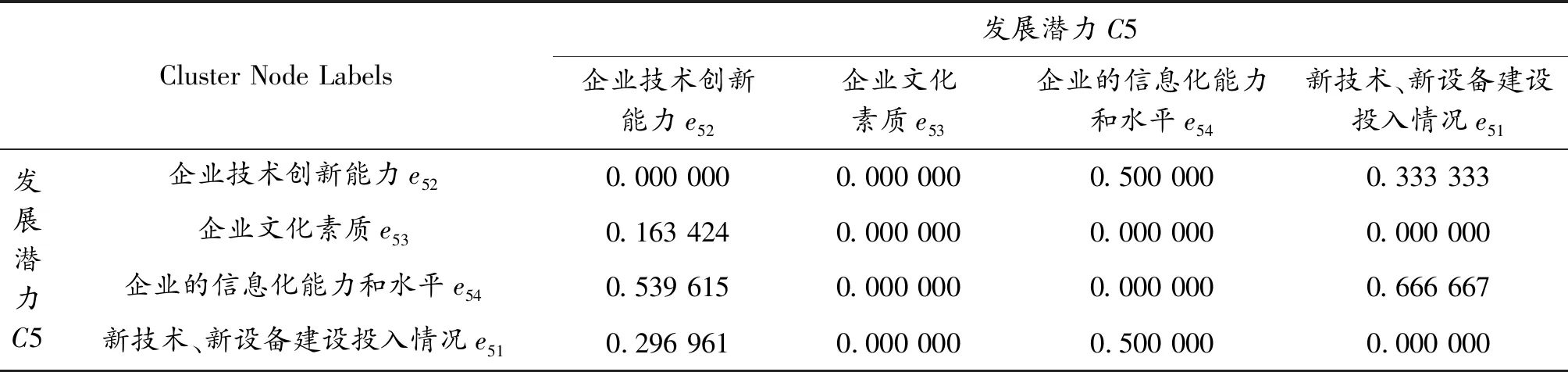
表2 C5指标集中未加权超矩阵中各元素值

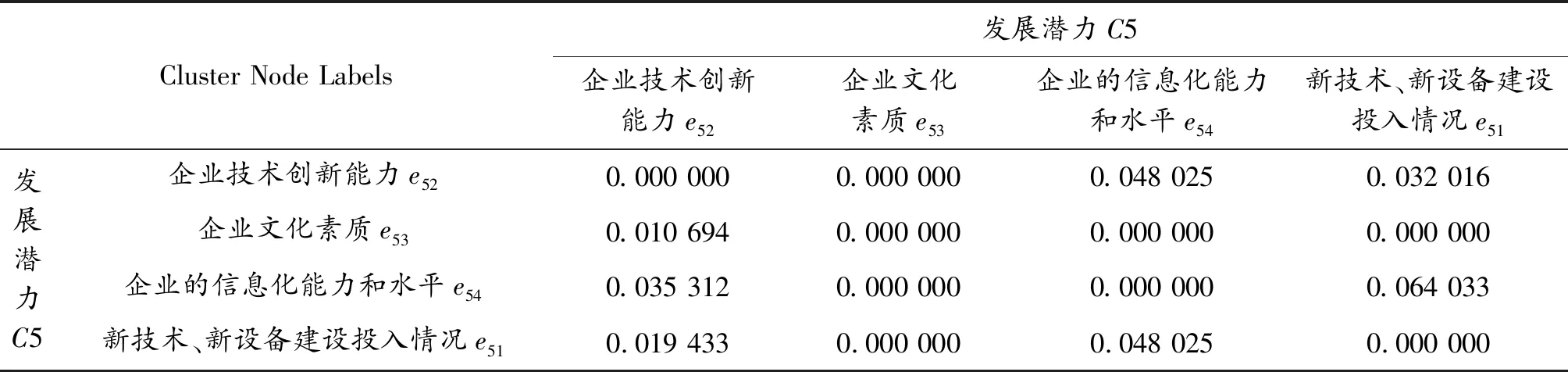
表3 C5指标集中加权超矩阵中各元素值

3) 计算极限超矩阵，确定综合权重

计算集内权重和综合权重如表4所示。

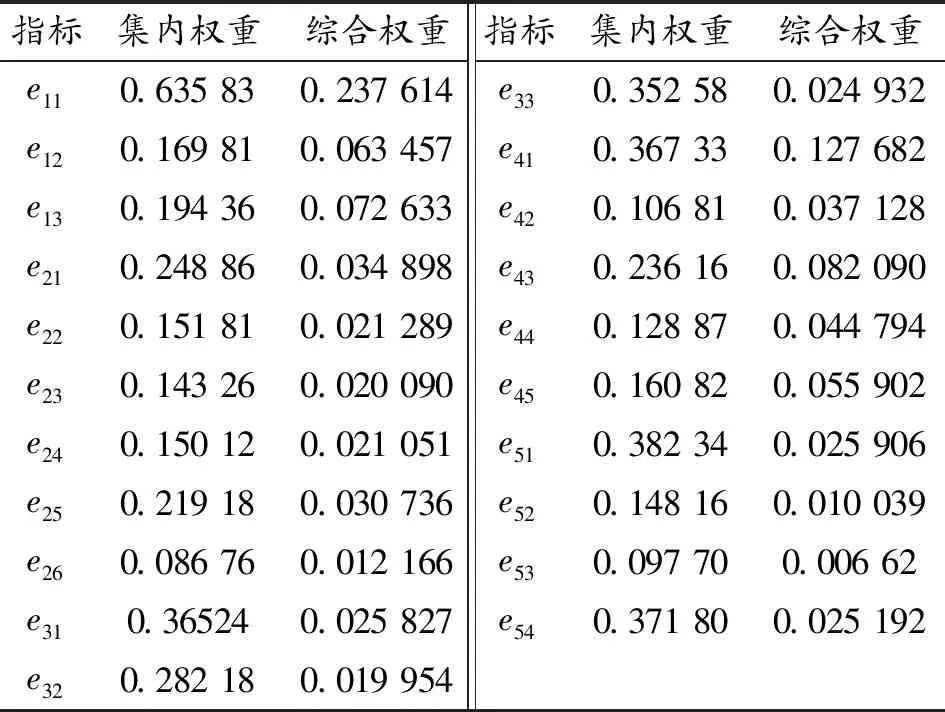
表4 集内权重和综合权重

2.4 结果分析

通过ANP网络模型可知，对通用装备维修合同商保障能力影响因素权重较大的指标有：企业信誉情况e11(0.236 717)、管理法规制度完善性及实施情况e41(0.127 104)、管理团队素质e43(0.082 074)，与实际情况相符。可见，部队在选择通用装备维修合同商时，关键还是要对企业信誉情况进行综合衡量。对大量通用装备进行维修保障，最重要的是与信得过的企业签订合同。再者，从排名前几的因素来看，部队关注的是企业整体的能力，而不是单单考虑个人素质的大小。

3 结论

与运用传统AHP法进行分析相比， ANP法克服了对影响因素的关系间单一和独立的不足，充分考虑了各影响因素之间的相互作用和反馈关系。通过对各影响因素进行两两比较，利用超级矩阵的形式量化影响程度大小，最终确定出各影响因素的权重。