一种长机故障情况下机群编队协同定位算法

刘晓洋,徐胜红

(海军航空大学 a.研究生管理大队； b.控制工程系， 山东 烟台 264001)

面对现代战争日益复杂的作战环境，机群编队协同作战这种新型空战模式受到了越来越多的关注[1]。协同定位作为协同作战的关键技术之一，其定位精度的高低直接影响整个编队协同作战效果。目前，机群协同定位主要采用高低精度搭配的主从式结构，然而在编队执行任务时长机很可能在敌方的干扰作用下失去与僚机的通信，无法为编队协同定位提供高精度的定位信息，导致机群定位效果不佳。因此，如何在长机故障情况下实现协同定位已成为急需解决的重要问题。

针对机群编队缺少误差有界绝对导航信息的问题，文献[2]提出了一种基于CEC与捷联惯性导航(SINS)组合的相对导航算法，提高了平台的导航精度，弥补了SINS误差随航时积累的不足，但该算法无法满足动平台编队协同作战的要求。文献[3]在无GPS条件下，提出了一种基于机间相互测距信息并利用几何图形平移旋转来估计各飞机导航误差的方法。该方法有效延缓了惯导位置误差的发散速度，但没有考虑飞机高度信息，只是在平面内进行了机群协同定位，且该算法需要机群队形的先验知识，有较高的局限性。文献[4]通过编队成员INS位置信息和机间测距信息作差得到量测值来提高各成员INS的位置精度，但该方法建立的模型维数过高，且各成员两两之间均要求通信，因此对计算机和数据链的要求较高。本文在对多平台INS输出信息进行最优综合实现INS误差修正[5]的基础上，提出了一种分布式机群编队协同定位算法，在保证长机失联前后编队协同导航系统模型变动较小的情况下抑制编队整体定位误差发散。

1 问题描述与方案设计

协同导航系统定位算法结构如图1所示，长机搭载精度较高的INS/GPS组合导航系统，其他成员设为僚机，除搭载较低精度的INS之外，均配备有光电测距测角传感器等相对导航设备，用以测量与长机之间相对距离和方位等相对信息。长机通过机载数据链广播高精度导航信息，为僚机提供量测信息。当长机因被击落等原因与编队失去联系后，僚机无法获得高精度的量测信息，若仅依靠搭载的低精度INS则定位误差会迅速发散。

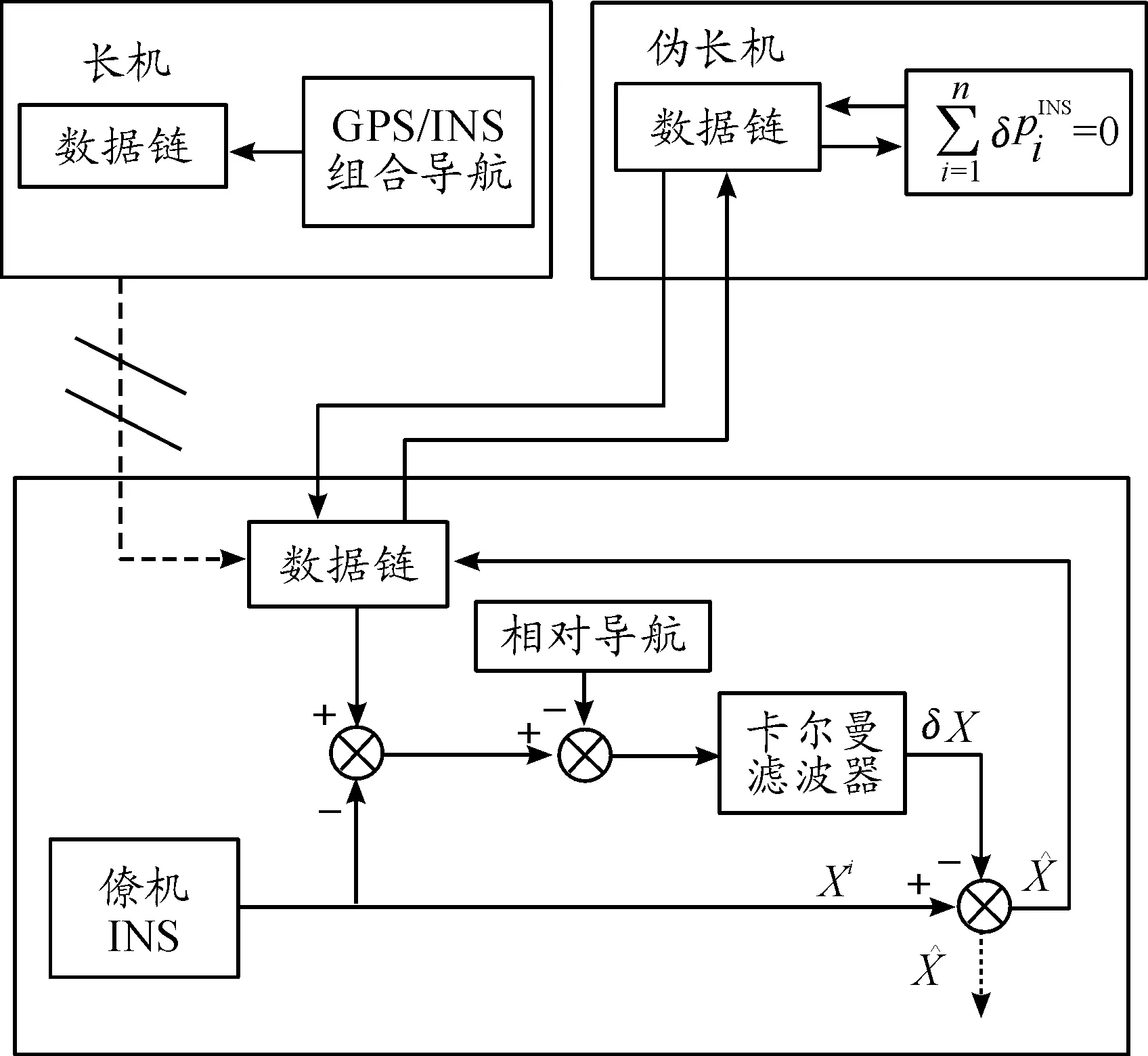
图1 协同导航系统定位算法结构

此时，可选择其中的某一架僚机作为相对导航参考点，视其为伪长机。伪长机的选取可依据与其他无人机的距离关系，假设僚机i与僚机j之间的直线距离为dij，则僚机i与编队其他成员的距离和Di可以表示为

选作伪长机的僚机i所对应的Di应满足以下关系：

Di=min(D1,D2,…,Dn)

选定伪长机后，其他僚机一方面以伪主机为基准点测量相对距离和相对方位等相对导航信息作为僚机卡尔曼滤波器的量测信息，另一方面通过机载数据链向伪长机提供通过僚机卡尔曼滤波器得到的状态估计。伪长机与长机类似，通过机载数据链为僚机提供量测信息，不同之处在于，除了提供量测信息外，伪长机卡尔曼滤波器还反馈其状态估计给僚机用于重置僚机状态。自此，整个机群编队构成了一个卡尔曼滤波闭环系统。为了更加简洁地说明算法，本文以3机为例建立系统模型。

2 系统数学模型

2.1 僚机部分系统方程

选取地理坐标系为导航坐标系(n系)，僚机 的INS误差状态方程为

(1)

式中，状态量Xi为

εbxiεbyiεbziεrxiεryiεrzi▽xi▽yi▽zi]T

系统噪声Wi为

其中，δλi、δφi、δhi为三维位置误差，δvEi、δvNi、δvUi为三维速度误差，εbxi、εbyi、εbzi为3个陀螺仪随机常值漂移，φEi、φNi、φUi为平台坐标系与导航坐标系之间误差产生的3个平台失准角，εrxi、εryi、εrzi为3个陀螺仪一阶马尔科夫漂移，▽xi、▽yi、▽zi为3个加速度计一阶马尔科夫漂移。

僚机i状态方程为自身INS与伪长机INS误差状态方程的叠加，即

(2)

如图1所示，在导航坐标系(n系)中，僚机i量测值Zi是由僚机i通过数据链收到的伪长机INS信息与自身INS信息和僚机测量的相对导航信息依次相减得到的，即

(3)

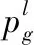
(4)

结合式(3)和式(4)可得僚机状态量与量测值的关系为

(5)

由于系统模型是在n系下建立的,而相对导航的测量是以机体坐标系(b系)为基准，因此需要对相对导航坐标转换。在b系中，僚机测量的相对导航信息存在误差，通过激光传感器测得的相对距离、仰角和方位角均可分为真实值与误差值两部分，将如图2所示沿着b系三个坐标轴方向分解，有

(6)

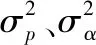
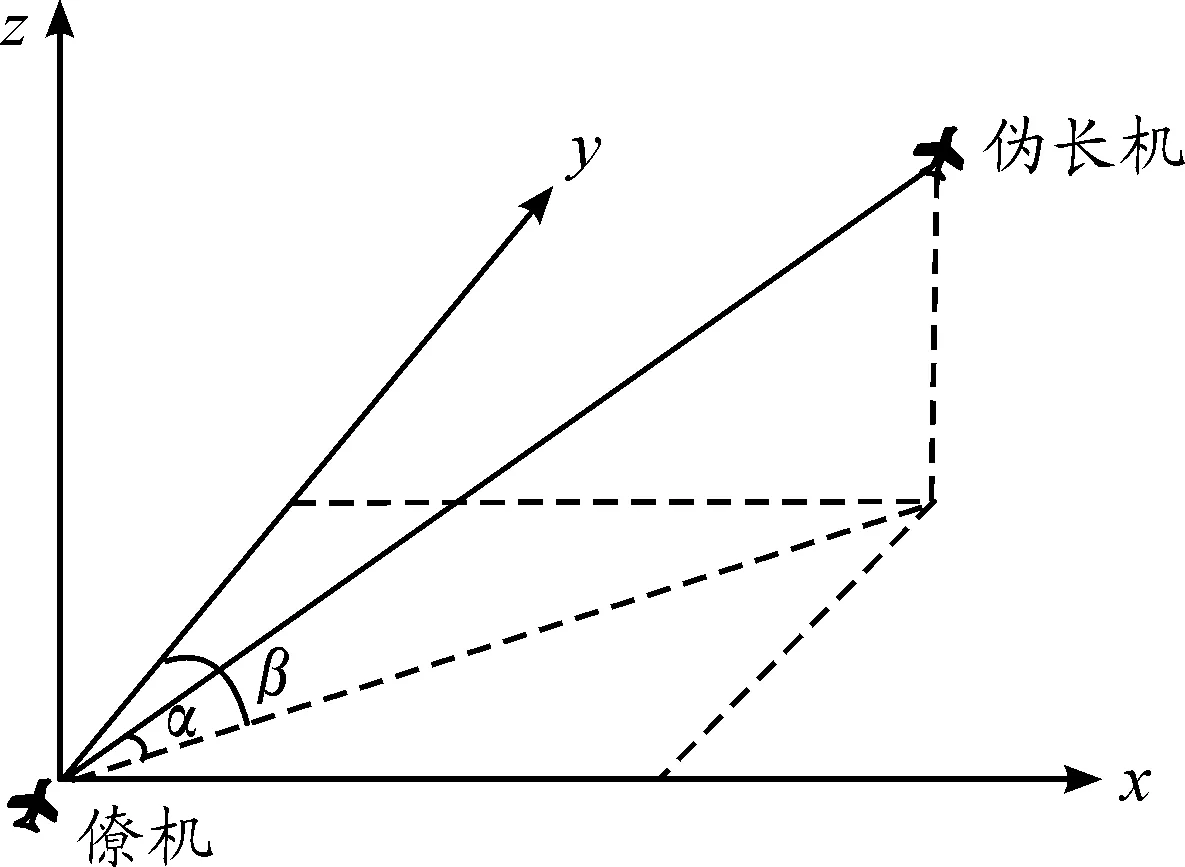
图2 僚机相对速度(位置)测量示意图

假设相对导航测量误差比较小，则有cos(ωα)≈1、cos(ωβ)≈1、sin(ωα)≈1、sin(ωβ)≈1，忽略高阶小量，即φvωα≈0、φvωβ≈0、φαωβ≈0，式(6)可以写成以下形式：

(7)

式中,

b系到n系的变换矩阵[6]为

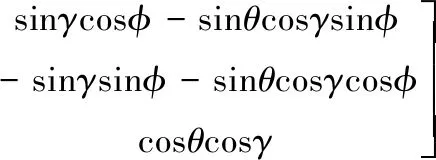
(8)

式中，γ、θ、φ分别为僚机真实横滚、俯仰和航向角，由于惯性导航系统解算的姿态角误差极小，用惯性导航系统解算出的姿态角可以近似替代真实姿态角，即

(9)

则由式(7)可以得到相对导航在n系的误差值为

(10)

INS输出的三维位置信息为经、纬、高，相对导航传感器输出的三维位置信息为三个方向的距离，常规单位是m，为了与相对导航距离信息量纲匹配，对INS输出的经度和纬度进行了转换

(11)

结合式(4)、(5)、(10)和(11)，僚机i量测方程为

Zi(t)=Hi(t)Xi(t)+Vi(t)

(12)

式中,

2.2 伪长机部分系统模型

伪长机滤波器的状态量是各编队成员状态的组合

由INS的误差服从正态分布特性可知，多套INS系统在同一位置工作时通过对其输出加权平均可以提高定位精度。

(13)

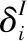
依据式(13)可以构造伪长机的量测方程:

ZG=HG·XG+VG

(14)

式中，ZG=0，VG=0，HG= [I3×303×15I3×303×15I3×303×15]。

3 滤波算法

机群编队协同导航系统的联邦滤波器由僚机和伪长机滤波器两部分组成，滤波算法的运行流程如图3所示。

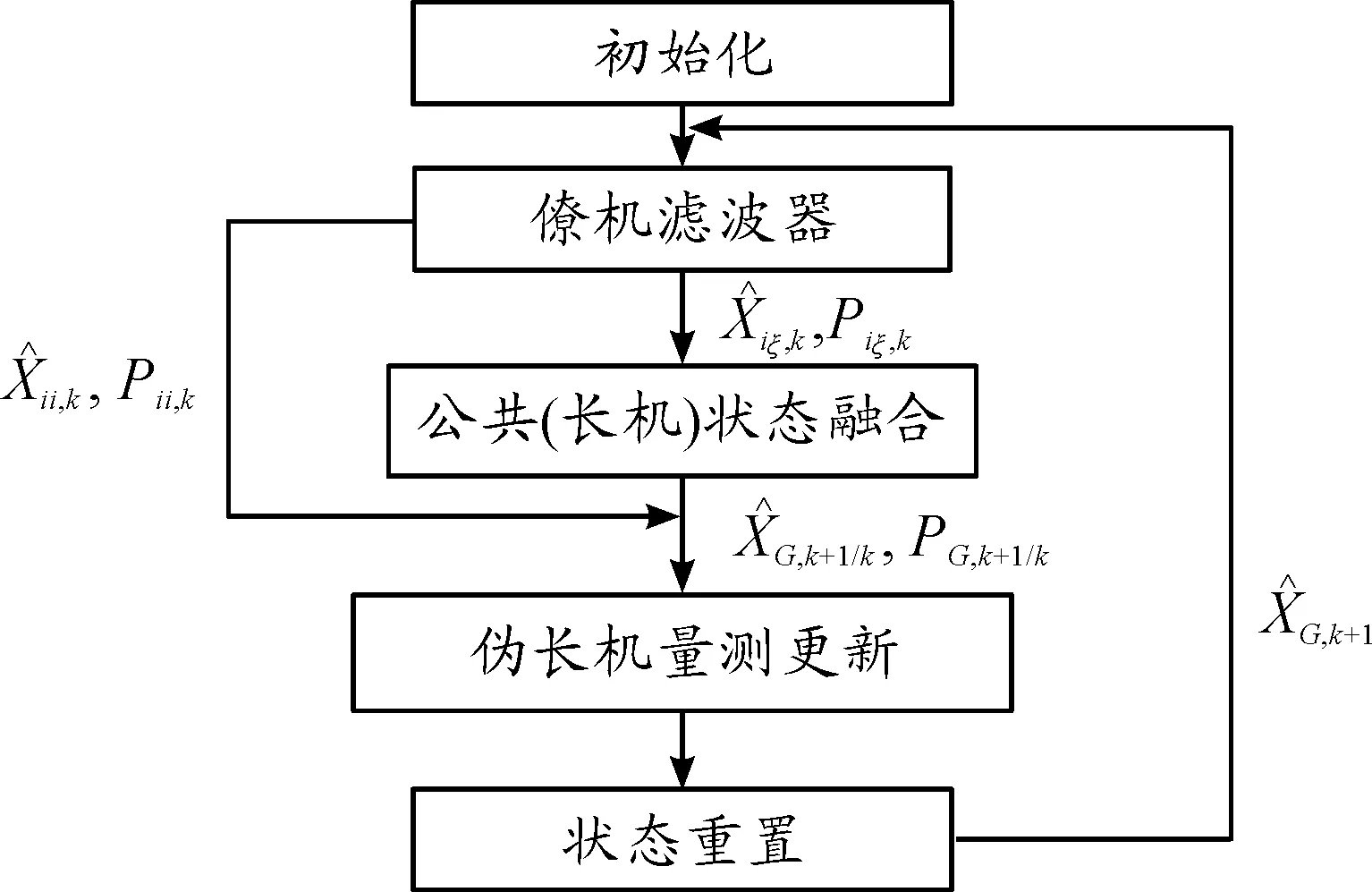
图3 滤波算法流程

1) 状态重置

利用伪长机滤波器状态估计重置各僚机滤波器的状态量，即

(15)

这样可以保证式(13)的约束能反馈给僚机，抑制僚机滤波状态估计误差发散。

2) 僚机滤波器时间更新和量测更新

各僚机部分滤波器独立地进行时间更新和量测更新。

时间更新

(16)

(17)

量测更新

(18)

(19)

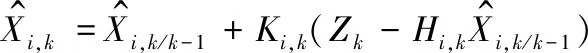
(20)

3) 信息融合

利用联邦卡尔曼滤波中公共状态估计的融合算法[7]，将各僚机部分滤波器得到的伪长机状态估计和其对应的协方差阵融合，得到除长机部分滤波器以外的全局估计。

(21)

(22)

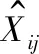
4) 伪长机部分波器量测更新

伪长机部分滤波器不进行时间更新，状态一步预测和协方差一步预测值由僚机滤波器状态估计提供，并且伪长机状态部分由融合后的结果替换。

(23)

(24)

由于长机部分滤波器不进行时间更新，因此其无需估计均方误差。这样主滤波器只需计算简化后的滤波增益和状态估计，即使主滤波器包含所有状态也能保证较低的计算量。

(25)

(26)

4 仿真分析

为了验证本文提出算法的有效性，进行了计算机数字仿真分析。在仿真计算中惯性导航和相对导航设备相关参数如表1所示。飞行航迹包括起飞、爬升、转向、匀速直线运动和降落等状态，仿真时间1 000 s。以北向为例，某一次仿真实验中3架飞机INS解算误差和滤波估计误差如图4所示。

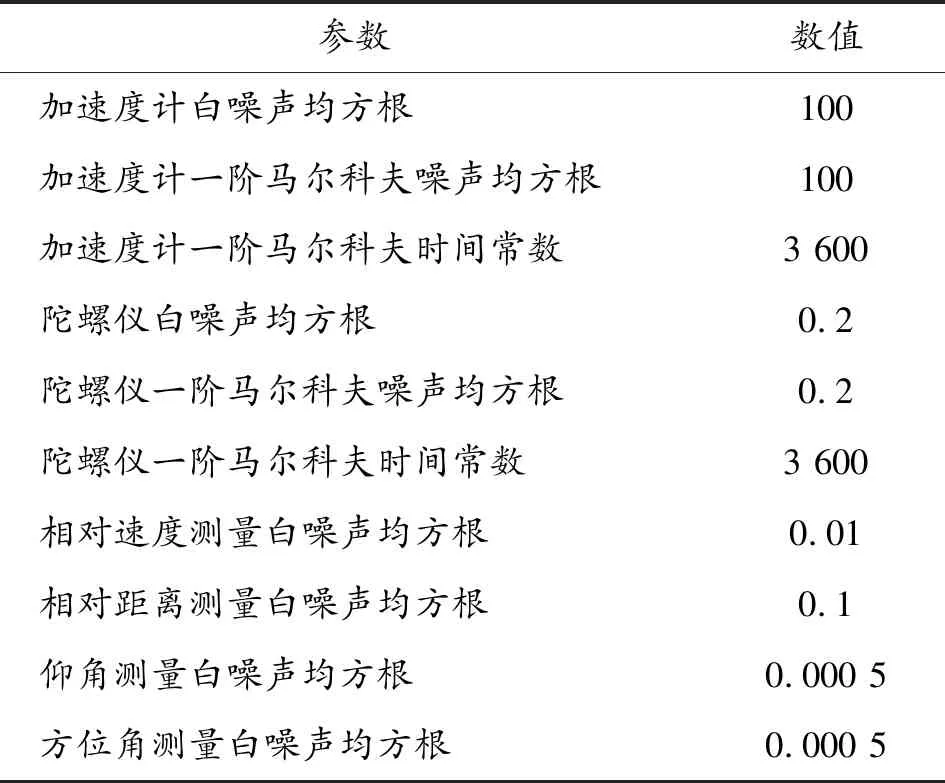
表1 INS和相对导航传感器的相关误差参数

图4为长机故障后编队各成员仅依靠自身惯性导航系统和采用本文所提协同导航算法后的北向定位误差。可以看出利用所提算法，各成员定位误差明显小于仅依赖INS时的误差，即协同定位误差的发散速度明显小于独立定位时发散速度。但图4仅为INS误差有正有负时的情况，若所有编队成员INS误差均为正或负，则最后结果只能说明协同定位使得各成员位置估计误差圆半径介于INS解算误差圆半径的最大值与最小值之间。即便如此，对于机群来说，其整体定位误差也优于各成员独自定位。

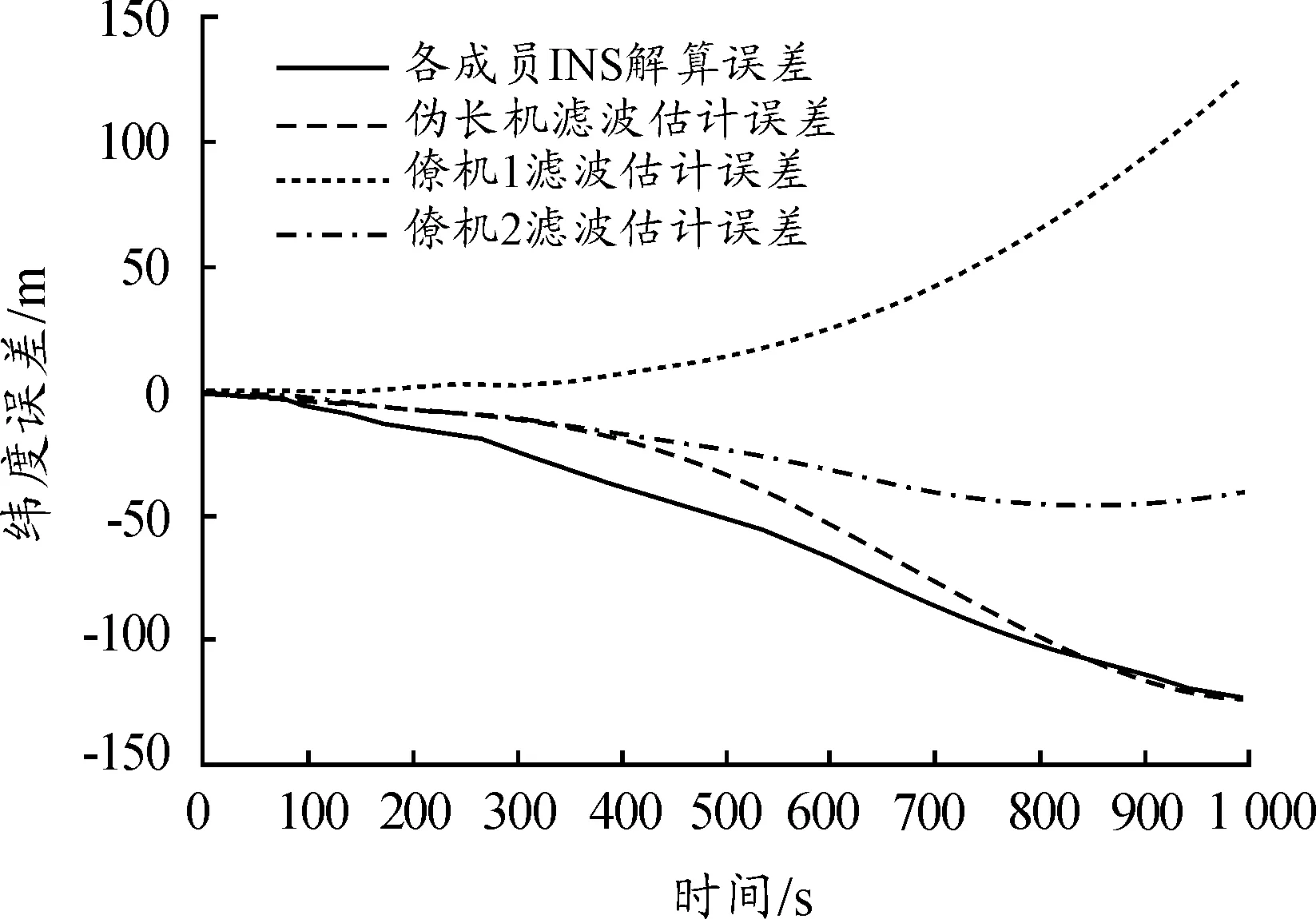
图4 编队各成员北向INS解算和滤波估计误差

由图4还可以看出，各成员协同定位估计误差曲线基本重叠，说明通过协同定位算法各成员位置估计误差大小极为接近。图5协同定位误差曲线局部放大进一步说明了这个结论。表2列出了仿真最后一步3架飞机INS解算误差值和协同定位估计误差值，直观印证了上述结果。

本文以3架飞机为例进行算法仿真验证，由于INS解算误差有正有负，随着编队成员数量增加，算法抑制定位误差发散的效果会越来越显著。

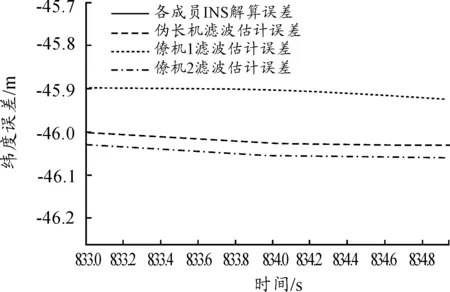
图5 编队各成员北向滤波估计误差局部图

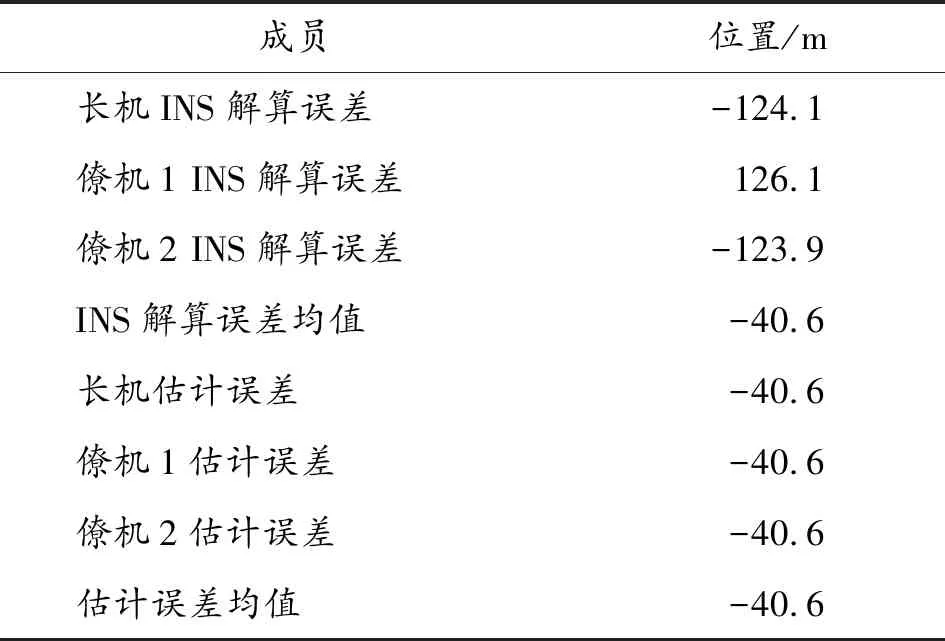
表2 编队各成员INS解算和估计误差

5 结论

1) 在建立协同导航系统模型的基础上，提出了基于同性能INS误差特性的机群编队协同定位算法。

2) 该算法对原有主从式协同导航模型改动较小，使机群编队故障前后能够迅速反应，保证了编队系统的稳定性。

3) 计算机仿真结果表明各成员定位估计误差为所有INS输出误差均值，算法起到了抑制编队整体定位误差发散的作用。