不锈钢车顶弯梁拉弯成形回弹缺陷分析

郑勇福 王 博 张 洋 柳铁伟 邴 政 王俊元

(中车长春轨道客车股份有限公司工程技术部，130062，长春//第一作者，教授级高级工程师)

拉弯成形工艺是不锈钢轨道客车车体钢结构冲压件制造中的关键工艺之一，主要用于车顶弯梁和立柱等弯曲半径比较大的板弯型材的弯曲成形。拉弯成形工艺的优势在于在板弯型材弯曲成形过程中通过同时施加轴向拉力和弯矩，改变型材内部的应力分布，加大材料的塑性变形量，消除弯曲过程中的起皱缺陷，减小回弹，提高成形精度[1]。

拉弯成形过程从表面上看，在专用拉弯设备的作用下型材产生弯曲变形，模具结构简单，过程简单。实际上在成形过程中拉伸力和弯矩的共同作用下弯曲和卸载时，型材断面内部应力应变的变化比较复杂。尤其是多段弧组合和直线与弧组合成的拉弯件卸载后,零件成形角度、弧长、断面形状都要发生变化,导致回弹量较难控制，外形精度难以保证。

本文以典型不锈钢轨道客车车顶弯梁为例，对拉弯成形中回弹缺陷的补偿问题进行分析探讨。

1 车顶弯梁拉弯成形回弹缺陷

1.1 拉弯模具常规设计方法和成形缺陷

某不锈钢轨道客车两种车顶弯梁分别为3段弧组合类型、3段直线与2段弧组合类型，如图1和图2所示。

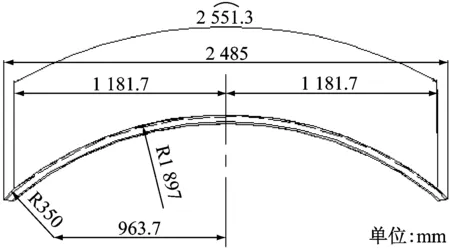
图1 3段弧组合车顶弯梁

两种车顶弯梁按常规模具设计方法是等弧长设计，对回弹则通过改变半径尺寸进行角度补偿。回弹补偿数值取得方式有两种。

(1) 经验值法：根据车顶弯梁结构尺寸、形状和材料性能，依靠设计者的经验和以往相似结构件参数给出拉弯成形回弹值进行拉弯模具的设计。通过反复进行拉弯试模、修模，最终生产出合格拉弯件。

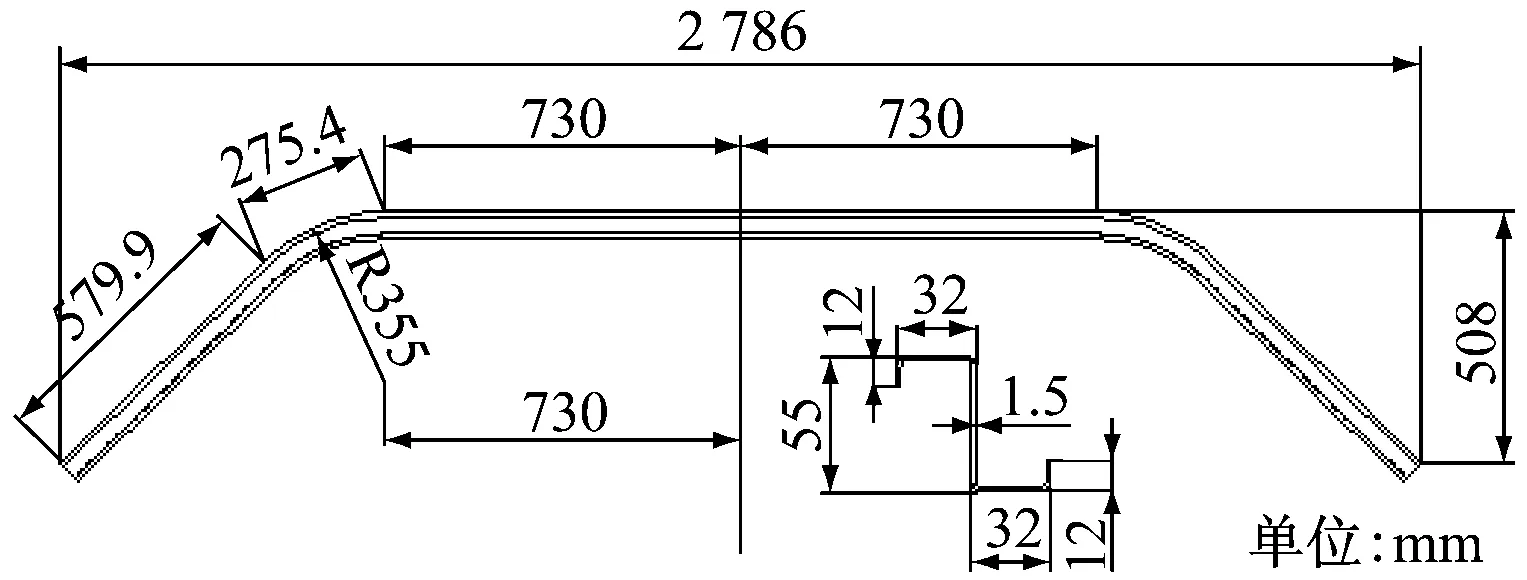
图2 直线与弧组合车顶弯梁

(2) 仿真软件数值模拟法：使用PS2F专用仿真模拟软件或其他冲压成形仿真模拟软件对拉弯成形过程进行数值模拟计算，得出回弹变形量和模具的数模曲线，直接生成模具图，然后进行试模调整。

车顶弯梁拉弯使用的设备为数控张臂式拉弯机(见图3)[2]，该设备可采用位移控制模式拉弯成形，在拉弯成形过程中通过程序控制拉弯夹钳运行轨迹来控制材料每一点的延伸量，实现边拉伸边弯曲，逐点逼近和包裹模具，最终实现车顶弯梁的成形。

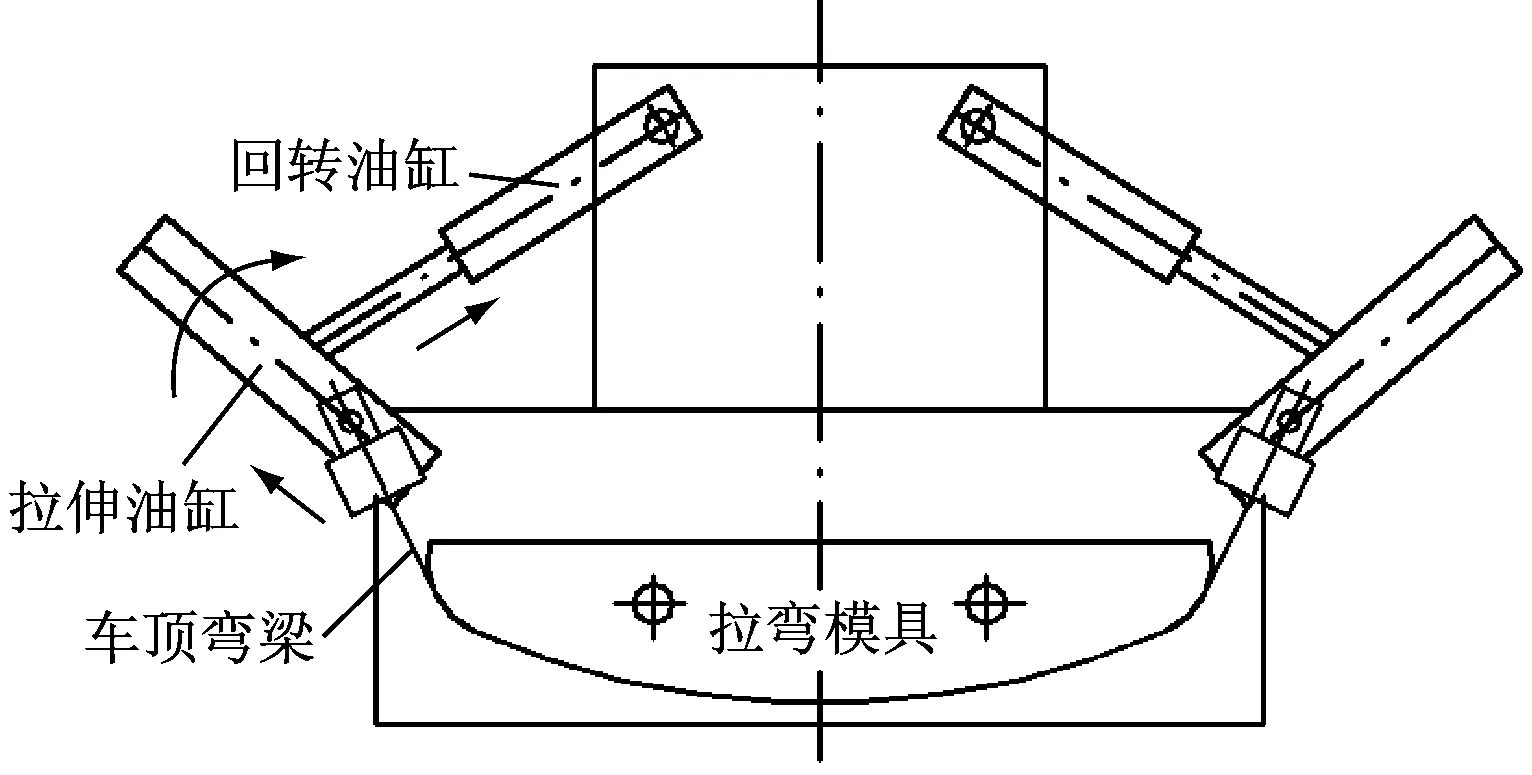
图3 数控卧式拉弯机工作示意图

按常规方法设计的模具最终拉弯成形后产生的回弹缺陷有3种：角度回弹、轴向收缩回弹、滞后回弹。以往仅对角度回弹研究较多，对后两种回弹缺陷往往忽略，以至于在模具设计阶段对回弹变形量的计算和补偿均存在误差。为此，分析研究车顶弯梁拉弯成形轴向收缩回弹、滞后回弹对提高车顶弯梁拉弯成形精度具有重要意义。

1.2 轴向收缩回弹

车顶弯梁拉弯成形轴向收缩回弹是指车顶弯梁拉弯成形卸载后材料沿型材中心轴线方向产生收缩变形。图4和图5为两种车顶弯梁最终拉弯成形后的样板检测外形状态。检测时一侧靠近样板，另一侧小圆弧处有间隙。产生原因是型材拉弯成形后中间段弧长变小，两切点向中心产生偏移。一般情况下实测最大间隙在2～4 mm。

图4 3段弧组合车顶弯梁轴向收缩回弹示意图

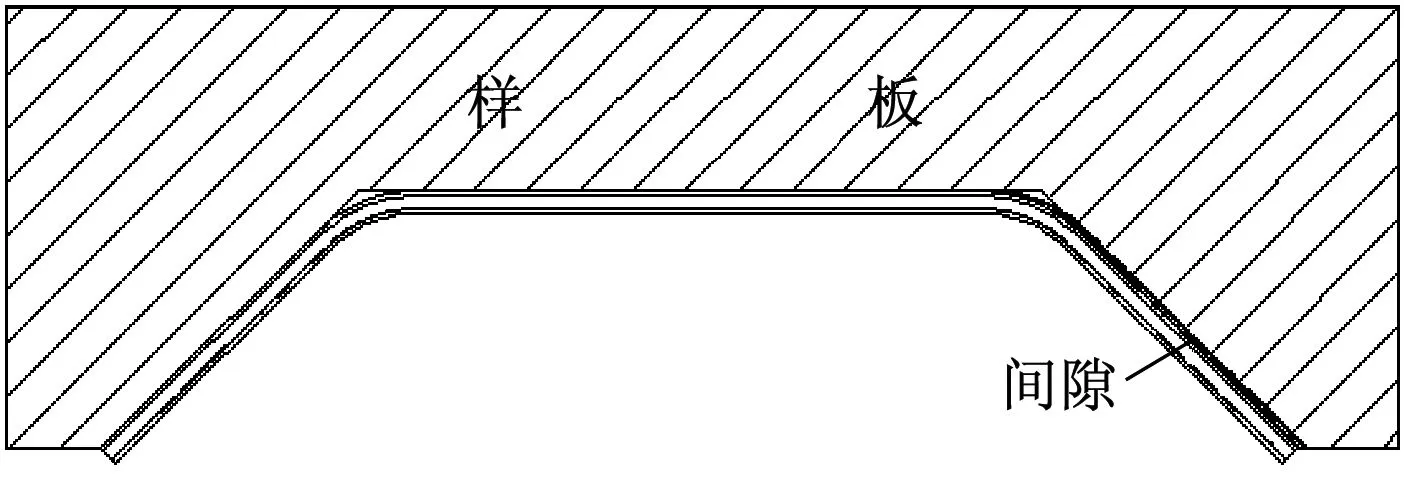
图5 直线与弧组合车顶弯梁轴向收缩回弹示意图

1.3 滞后回弹

在生产中发现不锈钢车顶弯梁拉弯成形卸载回弹后，除了产生瞬时回弹变形外，回弹现象没有停止，随着时间的推移一直继续发生着，既存在滞后回弹现象。具体表现为车顶弯梁的半径变大，角度外涨，这种现象据文献介绍在其他高强度钢以及铝合金成形中普遍存在[3]。滞后回弹现象对零件的成形精度及后续的组装使用中产生很大的影响。

图6所示为不锈钢车顶弯梁成形后自由放置24 h后滞后回弹状态。滞后回弹后如果间隙超过2 mm，零件将无法使用，需要进行二次调修。

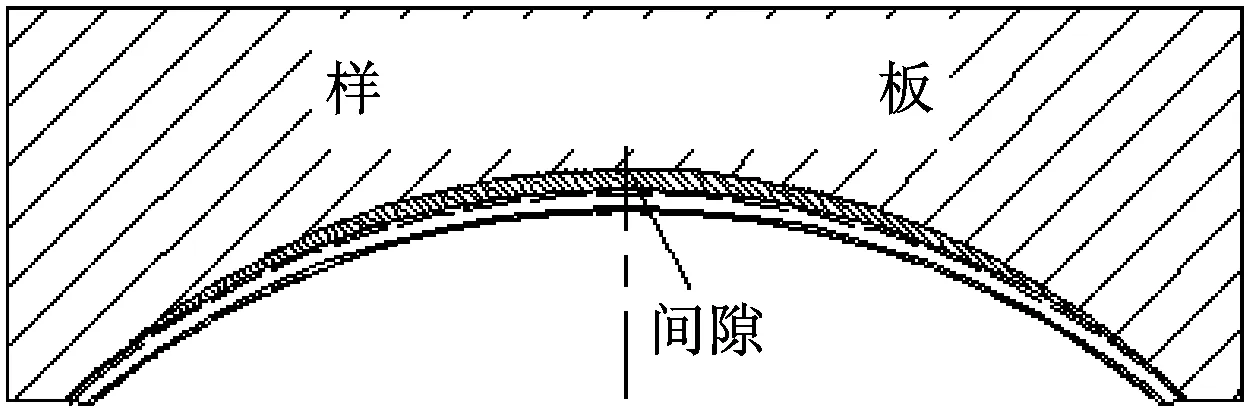
图6 车顶弯梁滞后回弹示意图

2 回弹缺陷产生原因及补偿措施

2.1 轴向收缩回弹原因及补偿措施

车顶弯梁拉弯成形过程的基本路径有预拉伸—拉弯—补拉(选择性使用)3个阶段。

从图7中可以看出，在拉弯成形过程中，拉伸应力和弯矩产生的应力合并后型材断面内全部处于正应力的状态，弯曲中性层已经移到型材外部。拉弯件卸载后由于内外皮部分产生应力应变差，将产生回弹变形，释放应力，使之回到平衡状态。其中图7中三角形部分产生角度回弹，矩形部分产生轴向收缩回弹收缩。

回弹的产生是因为使用的材料为金属材料,属于弹塑性材料，不管材料变形到何种程度,始终存在着弹性应变部分εp和塑性应变部分εe(见图8)，卸载后弹性应变部分要回缩。弹性应变的大小与实际变形量有关。需要进行试验或者模拟计算来确认回弹量。

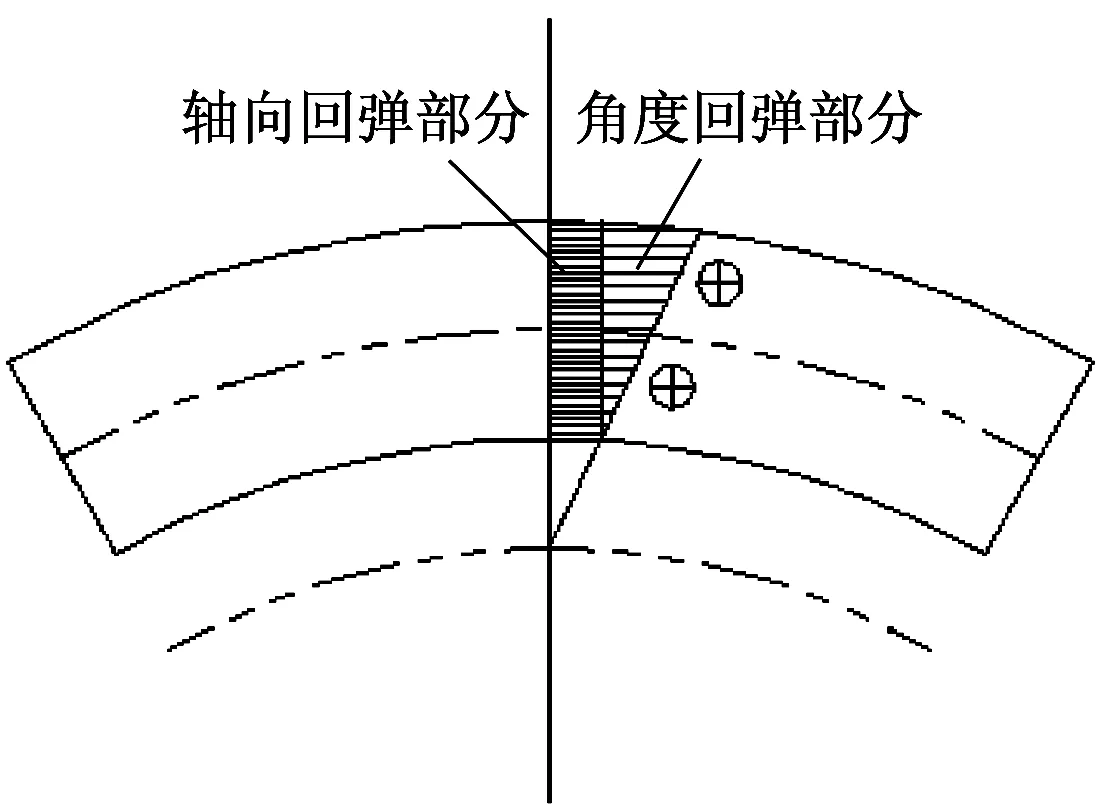
图7 车顶弯梁拉弯成形的断面应力分布

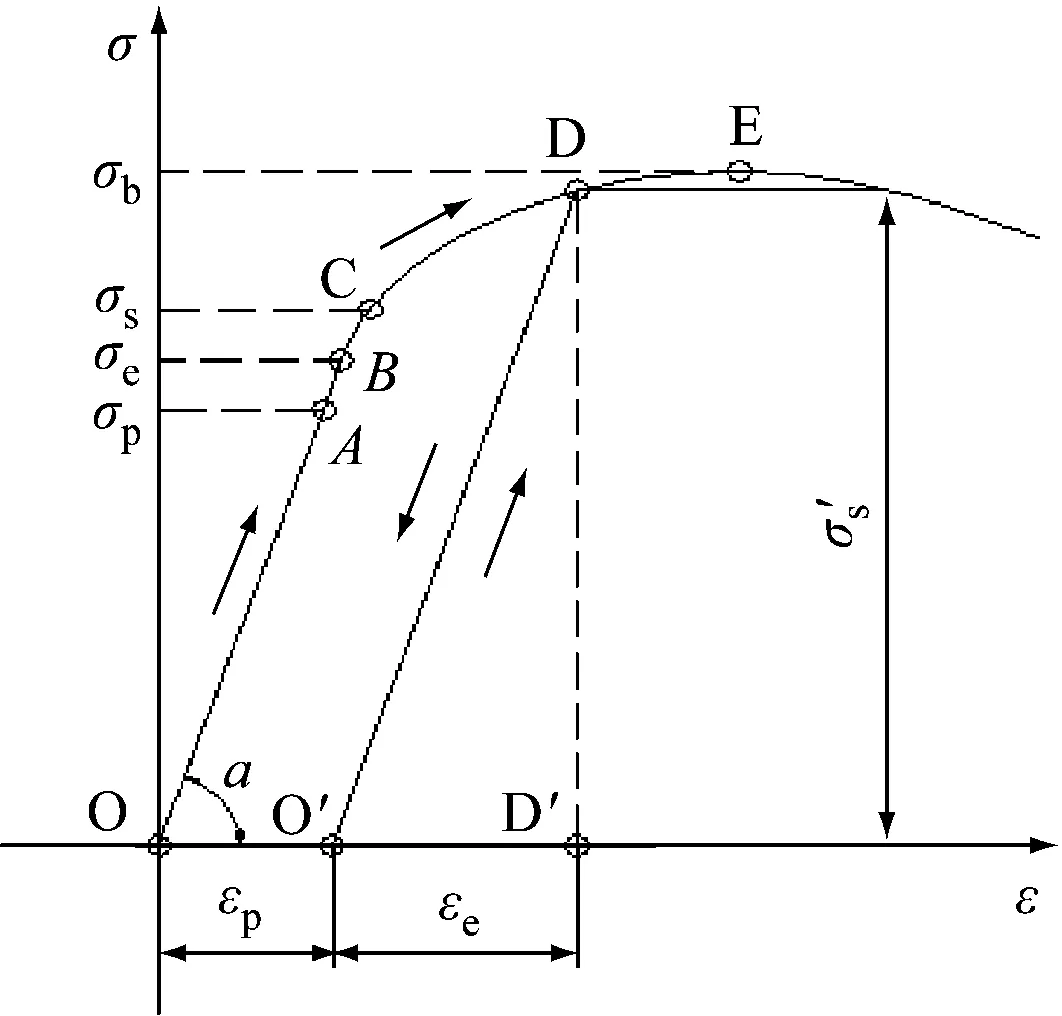
图8 金属材料应力应变曲线

为了证明拉弯成形中的轴向收缩回弹现象和轴向收缩回弹在总应变中的占比，对1 mm和1.5 mm厚SUS301L-ST不锈钢板和1 mm厚的6005-T4铝型材板进行以下数值模拟分析试验(见图9)：采用国标中的单向拉伸试验方法，试样的平行段长度为50 m；单向拉伸试验中一端固定，另一端拉伸；按照3.1%(即单向拉伸变形量为1.55 mm)、4.5%(即单向拉伸变形量为2.25 mm)和15%(即单向拉伸变形量为7.50 mm)的变形率进行模拟计算；然后卸载，并计算回弹后的拉伸变形量。由表1可以看出，回弹值与材料的性能及实际变形量有关，与板厚无关。

图9 单向拉伸变形回弹模拟试验显示界面

表1 单向拉伸变形回弹模拟值

根据以上计算方法得到的该种材料回弹率在总应变中的占比，并按图1所示进行车顶弯梁轴向回弹收缩量的计算(弯梁材料为板厚1 mm的SUS301L-ST不锈钢板)。用PS2F软件模拟拉弯成形过程的应力应变状态(见图10)，弯梁型材内皮部分的平均延伸率为3.1%，切点之间圆弧弧长l为2 553.13 mm，则收缩量为：

Δl=l×δ=8.68 mm

式中：

δ——回弹率，%。

以上模拟值基本与实际模具的补偿量相近，该件弧长实际补偿量为9 mm。

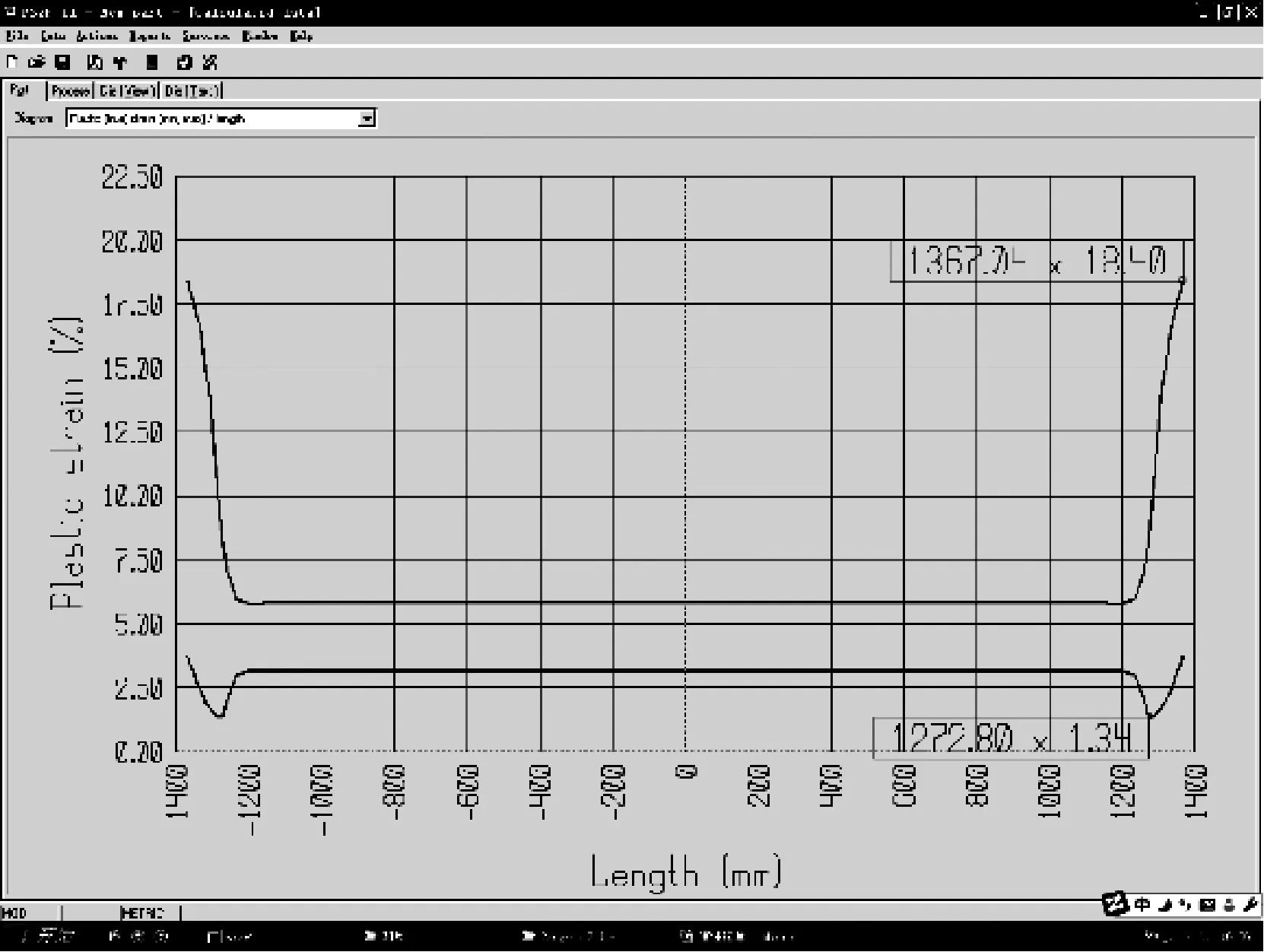
图10 3段弧组合车顶弯梁应变曲线模拟界面

图2所示的车顶弯梁中间直线段部分的拉弯成形总变形量，用PS2F软件模拟结果为4.5%(见图11)。中间直线段长度L为1 460 mm，直线段轴向收缩回弹收缩量为：

ΔL=L×δ=5.11 mm

以上模拟值基本接近实际回缩量。

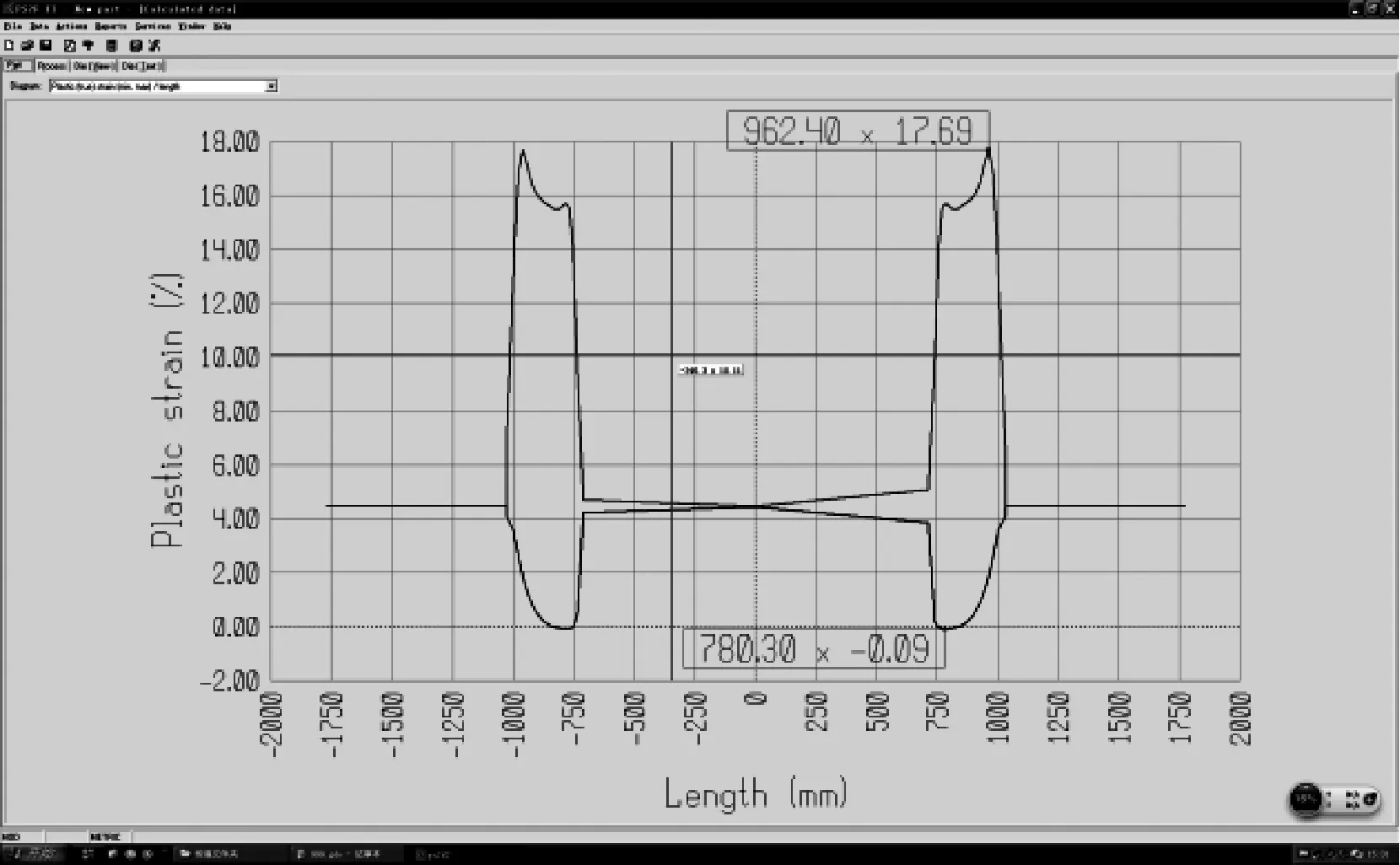
图11 直线与弧组合车顶弯梁应变曲线模拟界面

2.2 滞后回弹原因及补偿措施

不锈钢车顶弯梁拉弯成形后产生滞后回弹，主要表现为随时间的推移，角度外涨，是典型的滞后回弹现象。滞后回弹产生的原因目前没有统一的观点,通常认为滞后回弹产生的原因是成形件卸载后内部应力不能完全瞬时释放，部分残余应力应变的释放有个过程,导致拉弯成形件在无外力作用下延时产生滞后回弹外涨。文献介绍的对滞后回弹的分析方法介绍较少，比较典型的是利用金属材料的黏弹塑性理论通过Abaqus软件建模进行分析模拟计算[4]。

根据黏弹塑性理论，材料卸载后产生回弹Δα总包括弹塑性状态下的瞬时回弹Δαs和黏弹性理论下的滞后回弹Δαz两部分，即

Δα总=Δαs+Δαz

对不锈钢车顶弯梁需要求出滞后回弹，关键是要求出滞后回弹在总回弹总中所占的比值。

不锈钢车顶弯梁滞后回弹主要发生在中间的大圆弧处，两端的小圆弧处几乎不产生滞后回弹变形，所以车顶弯梁的滞后回弹仅需补偿中间部分。

对图1所示车顶弯梁补偿值近似算法是：采用Abaqus软件数值模拟计算出该种材料在单向拉伸状态下滞后回弹与总回弹量值，通过模拟计算的车顶弯梁瞬时回弹量模拟数值反算出滞后回弹值。

由图12可见，1 mm厚SUS301L-ST不锈钢板在单向拉伸状态下，中间弧段在应变量为3.1%时，1 000 s后对应的总回弹量为0.174 3 mm，滞后回弹量为0.000 5 mm,换算结果为：

Δαz/Δα总=0.002 86

最终,根据车顶弯梁瞬时回弹量计算出滞后回弹值。测算中选择1 000 s后的滞后回弹量,其原因是该种材料滞后回弹曲线表明在1 000 s后的滞后回弹趋于稳定(见图12)。

图12 SUS301L-ST材料滞后回弹曲线

3 结论

(1) 车顶弯梁拉弯成形过程中,型材在拉伸力和弯矩的作用下,不仅产生角度回弹，还会产生轴向收缩回弹和滞后回弹，这会影响拉弯成形件外形精度。

(2) 拉弯成形轴向收缩回弹主要影响多段弧组成的拉弯成形件。这些成形件拉弯成形回弹收缩后弧长缩短，切点向中心偏移，降低了零件的的外形精度。产生轴向收缩回弹的原因是材料拉弯时处于正应力状态，卸载后弹性部分会产生收缩回弹。因此,在模具设计中,需要对此方向的回弹进行补偿。补偿方案是：对拉弯成形过程采用PS2F软件或其他软件进行数值模拟，确认中间段的实际变形量，再通过材料单项拉伸试验确定弹性收缩率，得出切点之间变化的回弹收缩值，并通过实际试模再进行调整补偿。

(3) 不锈钢车顶弯梁滞后回弹缺陷是因为拉弯件内部卸载后留有残余应力，而残余应力释放有时间过程所导致。滞后回弹与材料性能及变形量等有关。对滞后回弹的补偿量近似算法是:通过数值模拟得到拉弯成形中的应变量，通过Abaqus软件的单项拉伸模拟得到滞后回弹量与总回弹量的比值，然后近似计算得出补偿量。