中国碳金融市场价格跳跃扩散效应及风险研究

赵 昕，丁贝德

（中国海洋大学 经济学院，山东青岛 266100）

一、引 言

气候变化问题日益受到国际社会关注，已成为人类生存发展面临的共同挑战。当前以工业经济为主的人类活动，产生大量二氧化碳排放，加剧了以全球变暖为主要特征的气候变化问题。作为全球最大的碳资源储备国和最具减排潜力国家，中国目前缺少完善的交易体系，在国际碳金融市场中处境被动。为了实现减排目标，掌握市场领导权，中国从2013年开始逐步建立深圳、北京、天津、上海、广东、湖北、重庆和福建8个试点碳排放权交易平台，并在2017年开始尝试建设全国统一碳金融市场。值得注意的是，我国碳交易尚处于探索阶段，交易活跃度较低，经常出现连续多日无交易的现象，这导致碳排放权市场价格出现跳跃性波动，收益存在突增或骤降现象。此时，识别碳金融市场收益波动的跳跃行为，分析其跳跃扩散效应并度量动态跳跃风险，对当局及参与者加强风险控制、提高碳金融市场稳健性具有现实意义。

国外学者对碳金融市场的研究主要集中在三个方面。一是价格波动的动态溢出效应：Reboredo[1]建立条件自回归极差模型，发现了EU碳市场和原油市场之间价格波动的动态溢出和杠杆效应；Balcılar等[2]分析了能源期货与碳期货合约的结构性变化和价格波动溢出效果。二是如何精确刻画碳市场的价格变化：Byun等[3]发现GARCH族模型能够较好地预测碳期货波动，其中基于正态分布假设的GJR－GARCH模型预测效果最好；Chevallier[4]以欧盟EUA、CER的期货合约为研究对象，建立方差风险溢价模型，描述了欧洲二氧化碳交易价格的时变过程。三是捕捉碳交易价格的跳跃行为：Sanin等[5]建立基于混合分布假设的ARMAX－GARCH模型，从时变跳跃概率的角度对欧盟二、三阶段配额交易价格的动态波动进行分析，发现模型能够刻画EU ETS市场跃动特征；Kim等[6]根据贝叶斯理论建立SVJ和SVCJ模型，分析EUA期货价格跳跃波动。

中国试点碳排放权交易所自2013年运行以来，成交量和成交额不断增长，引发国内学者对碳金融市场价格波动溢出问题的关注：Zhang[7]分析了EU碳交易市场与化石能源市场间的价格动态波动溢出效果；汪文隽等[8]建立多元GARCH（1，1）－BEKK模型检验了广东、湖北、深圳碳市场价格的波动溢出效应；Wang[9]发现了碳市场和能源市场之间收益与波动的非对称溢出效应；孙春[10]通过DCC－MGARCH（1，1）模型，发现EU碳市场和中国碳市场之间存在明显的价格波动溢出效应，且EU碳市场对中国碳市场的溢出效应更明显。碳金融市场的风险度量也备受关注：张晨等[11]引入Monte Carlo模拟算法，构建Copula－ARMA－GARCH模型计算碳金融市场多源风险的整合VaR；杜莉等[12]建立GARCH、ARCH模型研究中国碳金融市场的价格波动，通过异方差分析各区域碳市场的极端风险；王婷婷等[13]采用不同的分位数回归模型对中国五大碳市场进行实证分析，发现QAR－GARCH模型更适合中国碳金融市场风险的刻画；邱谦等[14]建立基于正态分布、t分布和GED分布的三类GARCH模型，发现t分布度量碳金融市场的风险较为理想。

总体而言，现有文献鲜有研究中国碳金融市场价格的跳跃扩散效应。虽然王倩[15]分析了中国试点碳市场间的溢出效应，但采用不含跳跃因子的传统模型无法准确识别跳跃特征，并且在没有考虑跳跃行为的前提下，对碳金融市场进行风险度量，缺乏有效性。目前，学者们常用Duffie等[16]提出的SVCJ模型描述资产价格的时变跳跃特征，Eraker等[17]比较SV、SVJ、SVIJ、SVCJ模型后发现SVCJ模型对收益波动跳跃的刻画能力最强，Ignatieva等[18]又进一步探讨了SVCJ模型的指数放射效果。曾昭法等[19]、王垒等[20]也将SVCJ模型用于证券、股票和期货市场的波动跳跃研究。此外，Mcneil等[21]提出的极值理论为捕捉金融资产价格的极端波动提供了思路。鉴于此，本文运用SVCJ模型量化中国碳金融市场价格的跳跃扩散效应，并结合极值理论的POT模型，尝试建立SVCJ－POT－VaR模型度量中国碳金融市场的动态极端跳跃风险。

本文的贡献在于：一是采用SVCJ模型对中国6个代表性碳金融市场的收益进行估计，该模型能识别收益序列波动的跳跃行为；二是给出跳跃扩散效应测度指标，细致地探讨不同市场间的跳跃强度与跳跃信息传递特征；三是建立SVCJ－POT－VaR模型，在考虑收益率跳跃变化的前提下，度量中国碳金融市场的动态极端跳跃风险，并进行准确性检验，以期为全国统一碳金融市场的构建和风险防控提供实证支撑。

二、模型设定与构建

（一）SVCJ模型

连续时间分析框架下，SVCJ模型假设t时刻各碳排放权现货交易价格为Pt，取自然对数价格Yt＝lnPt，t时刻的价格波动为Vt，则该模型的动态过程可以表示为：

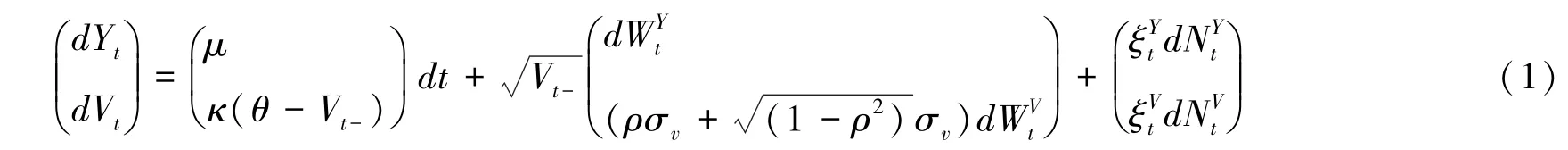
其中，t－表示时刻t之前的临近点；是具有顺势相关系数为ρ的标准一维维纳过程；参数μ度量资产价格的期望收益；κ表示波动均值回归系数；θ表示波动长期均值水平；σv代表波动的标准差；和是强度为λ的泊松过程，用来控制跳跃发生的到达时刻，模型假设收益与波动同时发生跳跃，即；表示跳跃幅度，其相关系数为ρJ，并满足。由于相关系数存在，该模型能够捕捉收益和波动之间的杠杆效应以及扩散项之间的关系。

本文采用基于贝叶斯理论的马尔科夫链蒙特卡罗（MCMC）方法估计模型参数，需要将连续时间框架下的SVCJ模型进行Euler离散处理。在选取日数据的前提下，令时间间隔Δ＝1，由此得到SVCJ模型的离散表达式：

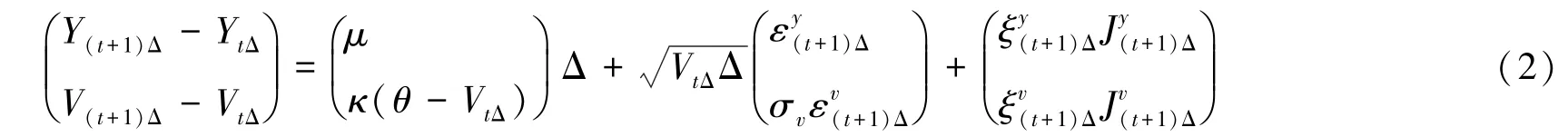
其中，Y（t＋1）Δ－YtΔ＝ln（Pt＋1）－ln（Pt），表示资产价格的自然对数收益率；Δ 是离散时间间隔，本文取Δ＝1；服从固定强度为λΔ的伯努利分布，其取值为0或1，取1时表示以λ的概率发生跳跃，反之则不发生；表示标准随机正态变量，其相关系数为ρ；其他参数的含义随机微分方程中保持一致。对Euler离散化的方程进行MCMC估计可能产生潜在偏差，因此本文选择提高迭代模拟次数，以减少离散化偏差，提高模型精度。

MCMC方法将未知参数和潜在变量看作随机变量，在 SVCJ模型中，待估的变量可以表示为，根据贝叶斯规则，待估变量的后验分布可以表示为似然函数、待估变量先验分布函数和某个标准化常数的乘积形式：

其中，c为标准化常数，V是波动过程，Y是T×1维观测值向量，Jy、Jv是跳跃次数，ξy、ξv是跳跃幅度，Θ是参数向量。为解决式（3）后验分布的复杂性和非标准型，本文选用基于Gibbs抽样的MCMC方法进行模拟，以产生平稳的马尔科夫链，得到后验样本的均值。

（二）POT模型

极值理论对金融资产价格的极端波动有较好的描述能力，主要包括区组最大值法（BMM）和超越阈值法（POT）。由于BMM方法对数据有季节性要求，因此在金融领域常用POT方法。该方法对给定的阈值，假设超越阈值的数据服从广义帕累托分布（GPD）。根据Mcneil等[21]的研究结果，采用标准化残差序列可以满足独立同分布条件。由（2）式易得到标准化残差：

当u→∞时，Fu（x）可以用GPD分布近似表示：

其中，β为位置参数，且β＞0，ξ为形状参数，若ξ≥0，x≥0，则GPD是厚尾的，若ξ＜0，0≤x＜－β/ξ。阈值可由Hill图法和平均超额函数综合确定。若Nu代表样本数据中超过阈值的数量，n表示样本总数，则F（u）可用（n－Nu）/n近似。Zt的尾分布可以表示为：

当置信水平为q时，的分位数可以表示为：

POT模型不需要对样本数据的整体分布做假设，受数据特征的影响较小，对我国碳金融市场进行刻画比传统模型更具有理论优势。

（三）SVCJ－POT－VaR 模型

风险价值（Value at Risk，VaR）已成为被学术界广泛认可的风险度量方法。VaR是指在市场正常波动、给定置信水平时，某一金融资产在未来一段时间内的最大可能损失。VaR可以直观地给出损失水平，数学表达式为：

式中，ΔP为金融资产在持有时间为Δt时的损失量，e为置信水平，VaR为最大可能损失。若按波动率是否具有时变性，风险价值可以分为动态VaR和静态VaR。静态VaR模型认为每个时点的波动率为持有期内的平均值，动态VaR则考虑了收益序列的波动集群特征与波动的时变性。

在SVCJ－POT－VaR模型中，首先对SVCJ模型进行参数估计，求得标准化残差，然后建立POT模型，求得的q分位数，最后通过式（9）计算求出收益率序列的动态VaR：

（四）跳跃扩散效应测度指标

对6个碳排放权现货交易市场的收益建立SVCJ模型后，本文对各市场的跳跃扩散效应进行测度。根据文献[22]统计思想，将跳跃扩散效应的测度指标定义如下：

1.跳跃扩散强度

跳跃扩散强度（Jump Diffusion Intensity，JDI）表示一个市场的跳跃引起其他市场发生跳跃的程度，主要描述市场间发生的跳跃行为在整个样本中的比重。假设跳跃发生在同日，其计算公式如下：

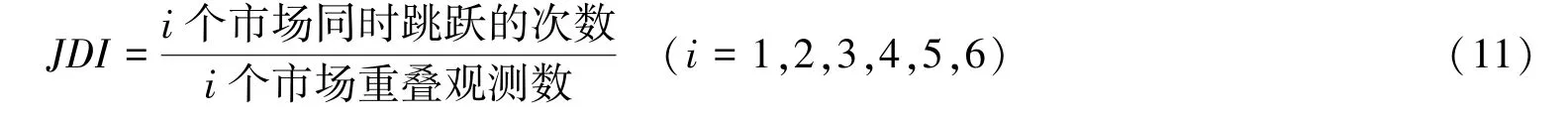
当i取6时，（11）式测算了中国碳金融市场的整体跳跃扩散强度，刻画了收益与波动的总体跳跃行为在样本区间内所占的比例。

2.条件跳跃扩散概率

条件跳跃扩散概率（Conditional Jump Diffusion Probability，CJDP）描述跳跃在市场间传播的可能性，即一个市场的跳跃信息在其他市场到达的概率。假设跳跃到达日相同，且不考虑市场间共同跳跃对其他市场的影响，给出下列计算公式：

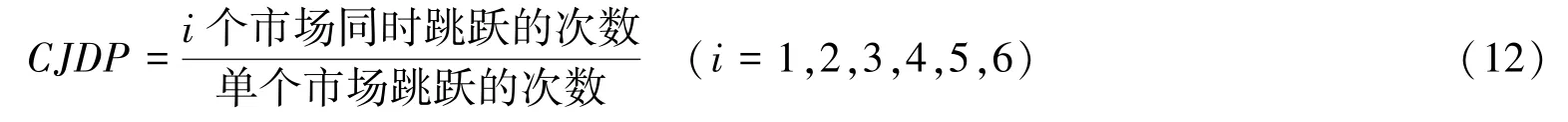
需要注意的是，跳跃概率的估计不再是0/1向量。为了识别跳跃行为，本文借鉴相关研究，给出了跳跃次数的公式：

其中，l为阈值，取跳跃次数概率的平均值；当跳跃次数的概率超过阈值时，表示识别到跳跃行为发生。

三、实证研究

（一）样本选取与说明

中国各碳排放权交易所只有现货交易，期货交易处于讨论设计阶段，因此本文以各交易所的现货交易数据为研究样本。样本分别来自北京、上海、广州、天津、深圳和湖北6个碳排放权交易所，数据来源为碳K线数据库。重庆碳排放权交易所的交易量长期低迷，缺乏活跃度，不作为研究对象。福建碳排放权交易所在2017年1月才进入运行阶段，数据量不满足模型要求，在此也不作考察。为了保证数据有效性，样本均取自2014年4月2日至2018年1月26日的每日成交价，取百分比自然对数收益率：

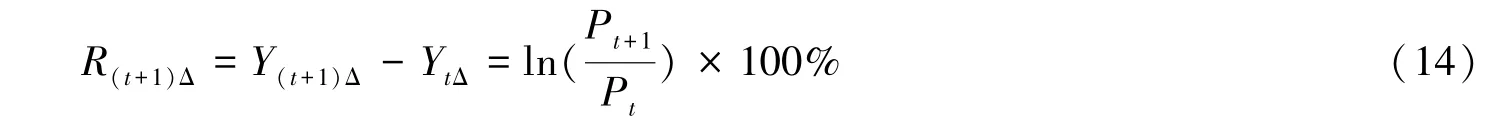
用SPSS 22.0对各碳排放权交易所的收益率序列进行描述性统计分析，结果如表1。

表1 各交易所收益率描述性统计

从表1可知，各收益序列的均值都为负，上海交易所平均收益率最高，广州最低；天津交易所的收益率极差和标准差最大，波动幅度最高；北京和湖北地区偏度为负，收益率序列呈现左偏；峰度系数均大于3，表明各碳排放权交易所的收益序列具有显著的尖峰特性。

最后，用ADF方法对数据进行平稳性检验，结果如表2所示。各交易所的收益率数据在1%、5%和10%的显著性水平上均小于临界值，因此认为各收益率序列平稳。

表2 各交易所收益率序列ADF检验结果

（二）SVCJ模型参数估计

在Gibbls抽样过程中，经过多次迭代可得到后验条件分布和参数估计值。Markov链在足够次数的迭代后，如果每个时刻状态的边际分布都平稳，则Markov链收敛。由于先验分布不会影响MCMC方法的参数估计值，本文选择先验分布为μv～N（0，1），μy～N（0，1），ρ～U（－1，1），ρJ～N（0，4），λ～Beta（2，40），利用winbugs迭代20 000万次，为保证Markov链收敛，选择前10 000个抽样值进行“燃烧”舍弃，用后10 000次抽样作为参数的稳定分布抽样，得到参数估计结果。见表3。

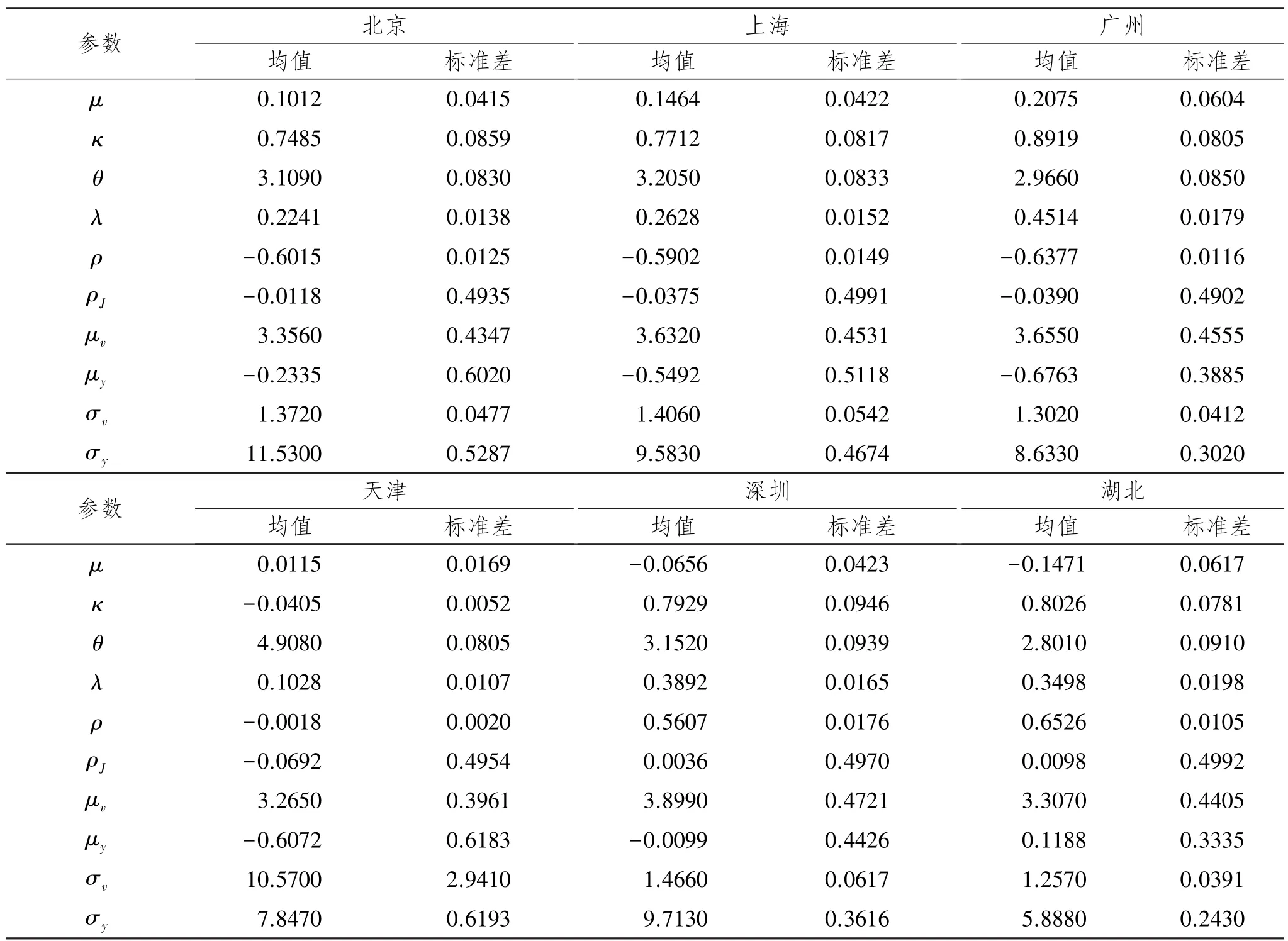
表3 SVCJ模型参数估计结果

由表3可知，期望均值μ较小，深圳和湖北市场为负，相对而言更小。天津的波动回归系数κ最小，表明随着碳排放权交易的进行，波动将持续更久，其他市场的κ值相近，波动向均值回归速度较快，波动缺乏持久性。天津市场的波动长期均值水平θ最高，表明市场活跃度提高、交易机制完善后，该市场的价格波动依然明显。波动跳跃的均值μv在6地均为正值，说明波动为正向跳跃，但收益跳跃的均值μy在湖北市场外均小于零，表明我国碳金融市场的收益以向下跳跃为主，受负面信息影响居多。北京市场的收益跳跃标准差σy最大，说明北京市场的跳跃变化幅度较大。σv显示在衡量波动的变化上，天津市场波动更活跃，波动绝对水平高，收益率数据的“厚尾”形态更加明显；其他市场则表现出一致的“平稳”波动特征。ρ与ρJ衡量了收益与波动之间的扩散冲击效果，在北京、上海、广州和天津均为负值，表明收益与波动之间存在显著的杠杆效应，深圳和湖北市场的杠杆效应则不明显。

图1展示了6个市场的跳跃概率、波动跳跃幅度以及收益跳跃幅度，根据式（13）的识别，北京、上海、广州、天津、深圳、湖北市场依次跳跃244次、286次、451次、154次、406次、344次。跳跃控制变量λ与跳跃频数呈现一致趋势，说明模型估计良好。总体来看，中国各碳金融市场的价格波动幅度较大，收益与波动有显著的跳跃行为，存在“断崖式”变化特征。

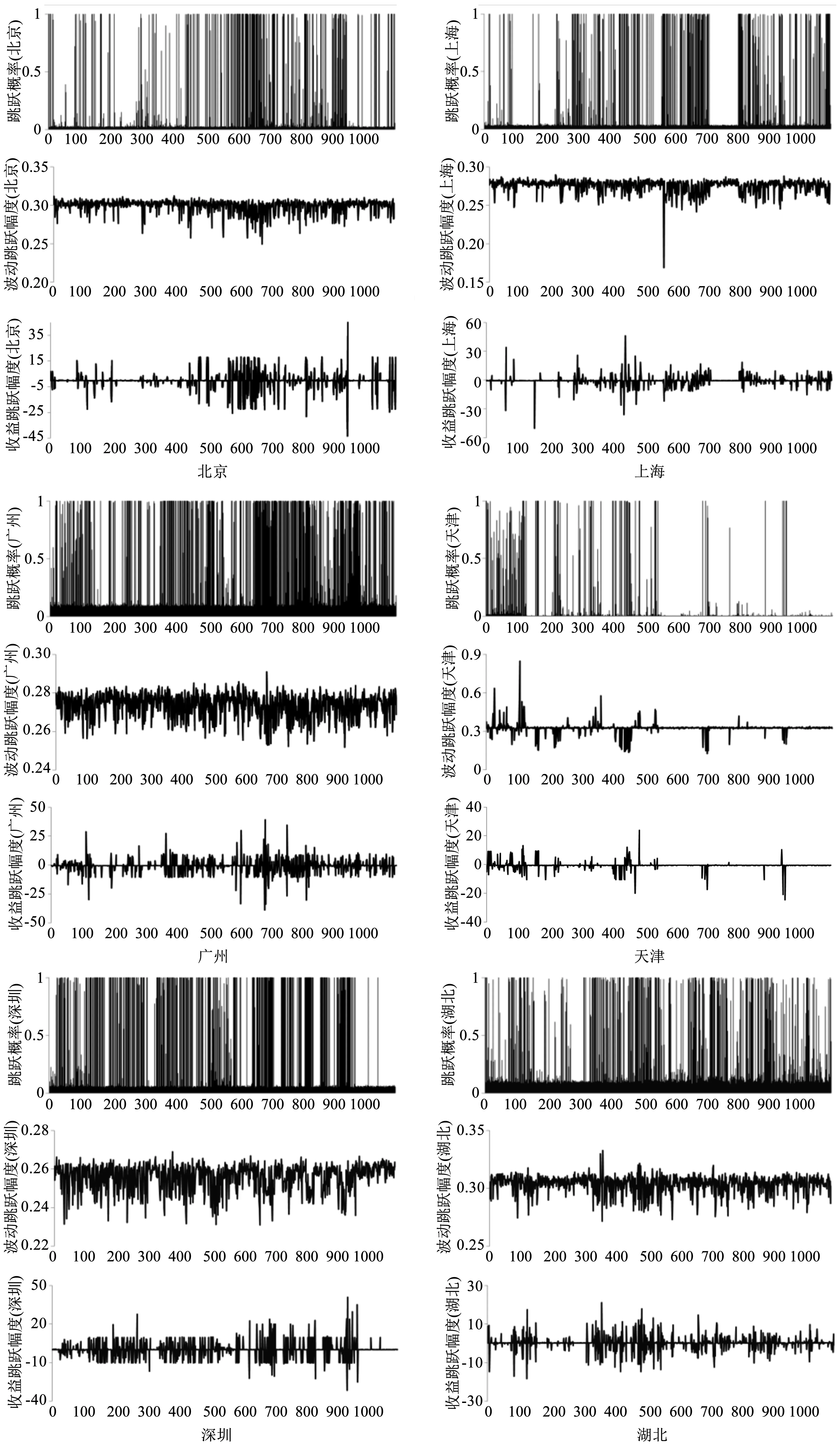
图1 6个市场的跳跃概率、波动跳跃幅度和收益跳跃幅度

（三）跳跃扩散效应分析

利用式（11）、（12）分析跳跃扩散强度和条件跳跃扩散概率，表4和表5列示了结果。

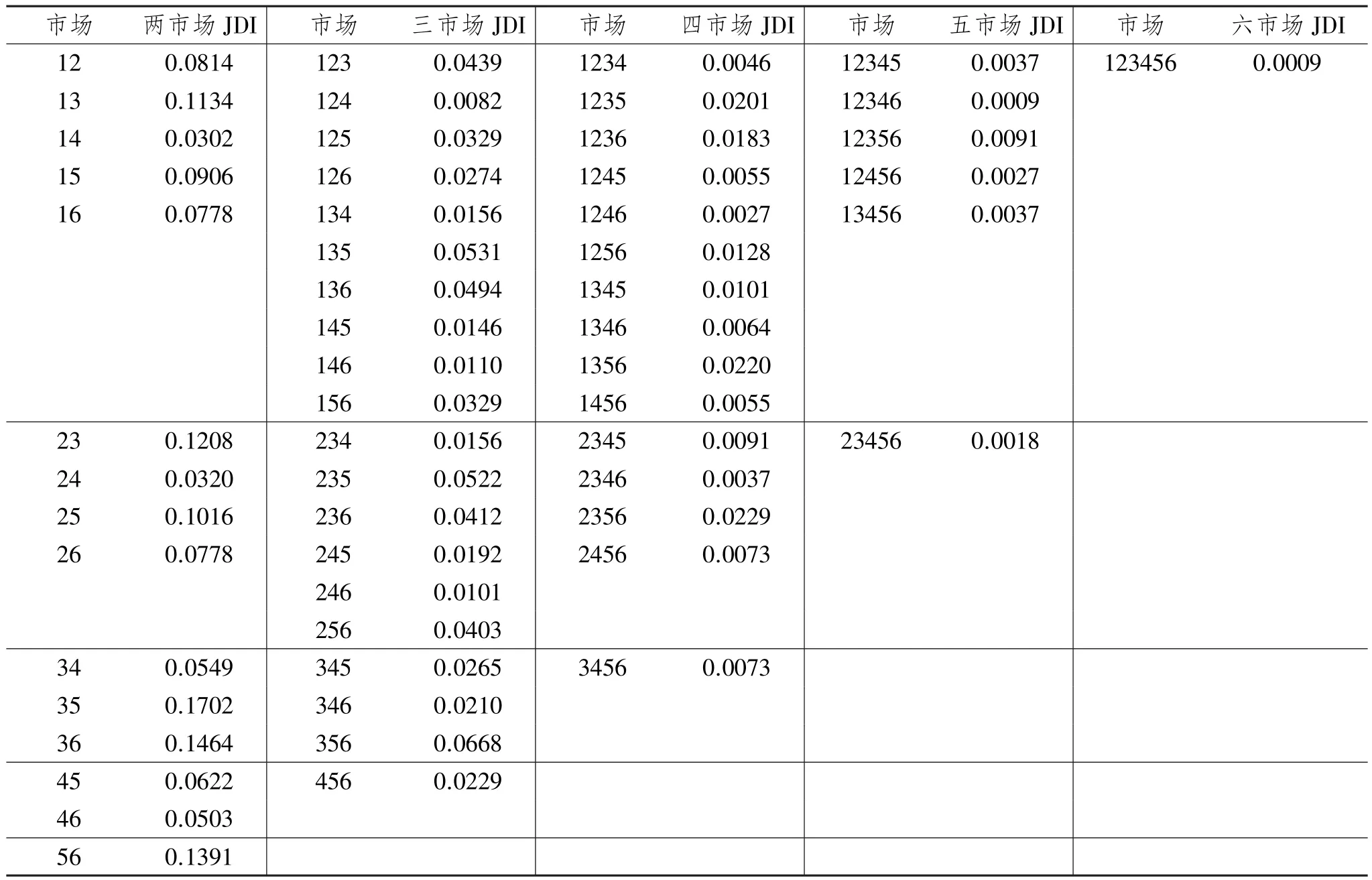
表4 6个市场收益的跳跃扩散强度

表4中，各编号组表示对应市场同时发生跳跃的在全部样本中的比重。两市场下，广州和深圳间的跳跃扩散强度最大，达到0.170 2，表示广州与深圳市场相互引起的跳跃行为占总体观测数的比例最高。三市场下，广州、深圳和湖北间的跳跃扩散强度最大，达到0.066 8，说明这三个市场的共同跳跃行为具有更强的一致性。当考虑四市场情况时，上海市场的收益跳跃行为与广州、深圳和湖北市场有更明显的跳跃扩散效果，因此这四个市场的跳跃扩散强度最高。五市场情况下，虽然北京、上海、广州、深圳和湖北市场间跳跃扩散强度最高，但总体来看共同跳跃行为逐渐减少，表明市场联动效果较弱，跳跃传递现象不够明显。六市场JDI考察了中国碳金融市场的整体跳跃扩散强度，然而仅有1次共同跳跃，强度为0.000 9，跳跃扩散强度微弱。

表5 6个市场收益的条件跳跃扩散概率

条件跳跃概率可以直观描述跳跃在不同市场间到达的可能性。限于篇幅，本文仅列示条件跳跃扩散概率前6大的情况。由表5可知，两市场下，广州的跳跃信息最有可能到达北京。三市场下，北京的跳跃信息引起广州和深圳共同跳跃的可能性最高。四市场下，上海市场的跳跃信息更充足，有0.196 7的概率引起北京、广州和天津市场的共同跳跃。五市场情况下，北京对上海、广州、深圳和湖北的条件跳跃扩散概率最高。六市场下考虑了单一市场的跳跃信息对全国碳金融市场的传递效果，天津市场的条件跳跃扩散概率最高，这与其波动跳跃较大的趋势一致。总体来看，单个市场的跳跃行为引起其他市场共同跳跃的可能性都较小，跳跃信息在市场间缺乏有效的传递路径。

（四）POT模型参数估计

计算动态VaR之前要先计算各收益率序列的静态VaR。根据SVCJ模型得到的参数估计结果计算标准化残差序列，通过POT模型和对数似然估计的方法估计GPD分布的形状参数ξ和位置参数β。本文利用R3.4.1的EVIR包绘制平均超额函数图和Hill图综合确定阈值μ。各样本序列的阈值及GPD分布参数结果如表6所示。

表6 GPD分布的参数估计结果与静态VaR计算值

图2分别给出了北京市场残差序列GPD拟合的超出分布图（左上）、分位数图（右上）、返回水平图（左下）以及密度直方图（右下）。由图2可以发现，超出分布图与分位数图基本围绕直线分布，返回水平图显示估计点基本分布在置信区间内，分布密度函数与直方图保持一致趋势，拟合效果较好。图2给出了不同阈值水平下的位置参数与形状参数变化，当u＝1.38时，参数保持稳定状态，因此阈值选取是合理的。

同样，对其他5个市场进行相同的诊断检验，参数估计依然保持有效性，限于篇幅，不再展示诊断检验图。

图2 北京市场的GPD参数诊断图

根据GPD分布的参数结果可以计算出静态风险价值。在95%的置信水平下，深圳市场的静态VaR最高，由价格波动带来的最大损失达到8.807 5%，天津市场最低，仅有2.673 9%。当置信水平提高到99%后，天津市场的静态VaR达到最高，说明在市场价格正常波动下，该地区碳排放交易的价格风险极大，这与极差呈现一致特征。

（五）动态VaR模型的后验分析

在静态VaR计算值的基础上，通过SVCJ－POT－VaR模型可以计算出各序列的动态风险价值。为了检验模型的准确性，本文采用Kupiec失败频率检验法[23]，将每日实际损失大于当日动态VaR值的时刻记为一次失败数。由于VaR代表一定置信水平和持有期的最大损失，因此取相反数表示，检验结果见表7。

表7 动态VaR的后验检验

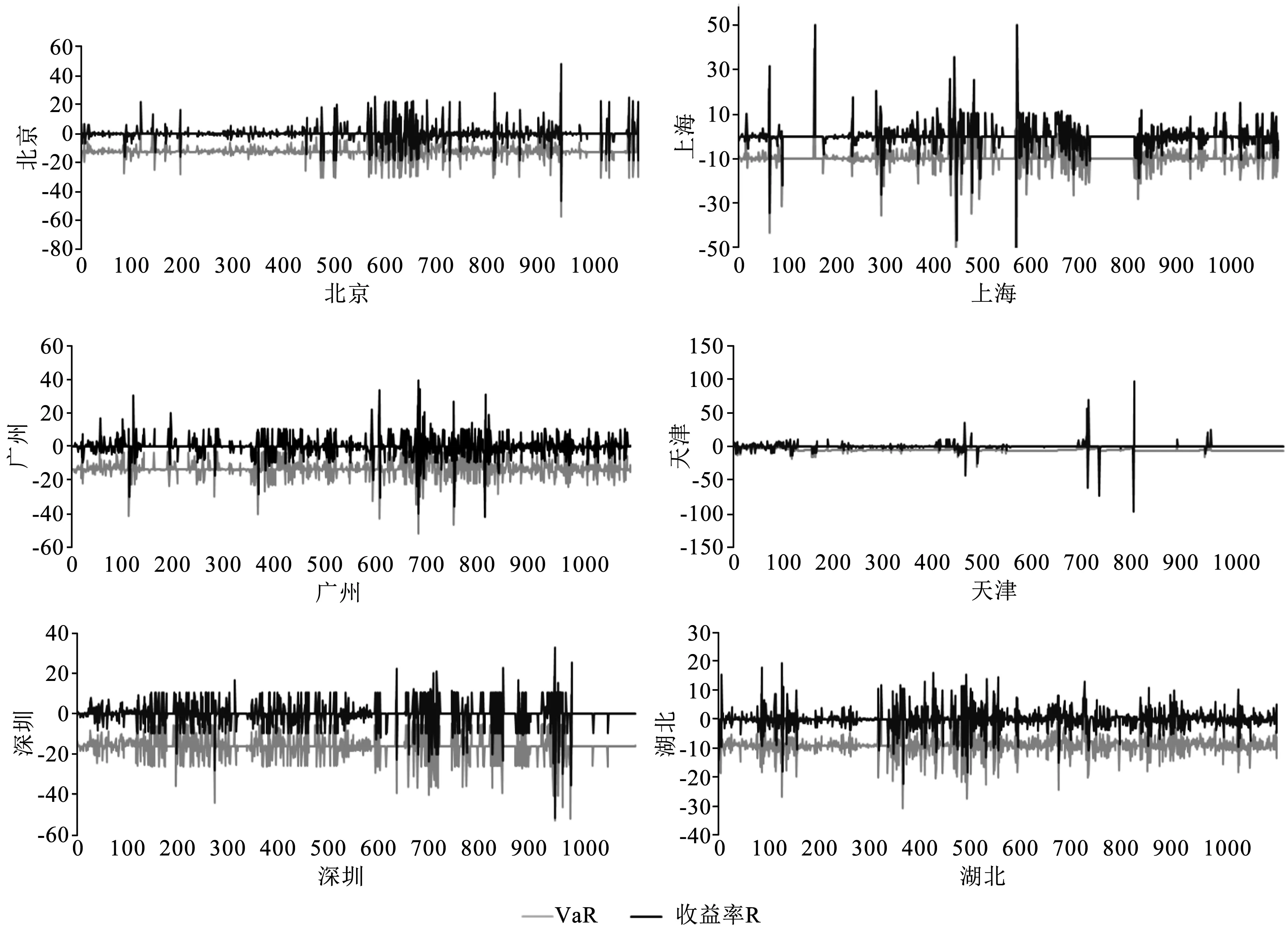
图3 95%置信水平下动态VaR与收益率序列对比

由表7可知，在95%置信水平下的Kupiec检验中，6个交易所LR统计量的p值均大于0.05，未拒绝模型有效性假设，表明考虑极端跳跃行为的SVCJ－POT－VaR模型对我国碳金融市场的收益率风险测度是合理的。99%置信水平下，p值大于0.01，LR统计量依然位于接受区域，模型通过检验。图3展示了95%置信水平下动态VaR与收益率序列的对比，可以发现SVCJ－POT－VaR模型能够有效测算中国碳金融市场的风险价值，当价格出现极端变化时，模型依然有能力捕捉到这种跳跃行为。

四、结 论

本文以中国6个代表性碳排放权交易所的百分比对数收益序列为研究对象，利用SVCJ模型捕捉收益的跳跃性变化，研究跳跃扩散效应，并对收益的跳跃现象构建了SVCJ－POT－VaR模型，测算各碳金融市场的动态跳跃风险价值，得到如下结论：

1.中国碳金融市场的收益率波动幅度较大，存在明显的跳跃现象，并且各市场之间存在跳跃扩散效应，还未形成一个统一稳定的碳金融市场。

2.广州和深圳市场的跳跃扩散强度更高，跳跃现象在全国碳金融市场中占较大比例，但6个市场的联动性较弱，整体跳跃扩散效果不明显。

3.天津市场的跳跃信息向其他市场传递的概率最高，市场稳定性最差，当出现不可控的政策调整或风险事件时，天津市场最有可能引起全国碳金融市场的波动。

4.在考虑收益率波动的极端跳跃性时，SVCJ－POT－VaR模型对中国碳金融市场具有良好的风险测算能力。

由此，中国碳金融交易的参与者要积极了解市场价格的跳跃行为及其扩散效应，避免极端风险事件引起的跳跃现象带来更多风险；同时，投资者和监管部门可以借助量化模型，对价格波动产生的风险水平进行监测，以保障中国统一碳金融市场稳健有效地运行。