鄂尔多斯盆地姬塬地区长6储层矿物含量与孔隙度的线性关系

李小燕 ，乔华伟 ，张建魁 ，马俊杰 ，闫江涛 ，李树同

（1.中国科学院兰州文献情报中心/中国科学院西北生态环境资源研究院,兰州730000；2.甘肃省油气资源研究重点实验室/中国科学院油气资源研究重点实验室，兰州730000；3.中国科学院大学，北京100049；4.中国石油长庆油田分公司第三采油厂，银川710065；5.中国石油长庆油田分公司第五采油厂，西安710020）

0 引言

目前，在全球常规油气资源产量日益降低的情况下，非常规油气资源量的开采是能源供给增产的主攻方向，然而非常规储层的低孔、低渗特征是影响资源开发的重要瓶颈。前人主要从沉积环境和成岩作用两大方面对储层的致密成因做了大量的定性研究［1-4］，但随着地质学研究逐渐向精细化、定量化方向发展，许多学者尝试从矿物含量与孔隙度的关系角度进行了半定量的研究［5-15］。对鄂尔多斯盆地主成分含量的研究发现，塔巴庙和苏里格东区石英含量与物性呈正相关，岩屑含量与物性呈负相关［5-6］，长石含量与物性关系不明显［5，7］；但在广安须家河组中，砂岩物性与石英含量、岩屑含量之间均无明显的相关性，而与长石含量呈正相关［6］。对胶结物的含量研究发现，在普光气田和鄂尔多斯盆地周家湾地区，碳酸盐胶结物含量和硅质含量与储层物性之间也具有良好的负相关关系［8-9］。对储层中黏土矿物含量与物性的关系研究发现，鄂尔多斯盆地中生界砂岩储层中伊利石和高岭石含量对孔隙度几乎没有影响，自生绿泥石对孔隙度的影响则具有两面性［10］，但在环江油田延长组中，伊利石含量与孔隙度之间呈负相关性［11］；在苏北盆地台兴油田阜三段和泌阳凹陷1009井中，高岭石含量与孔隙度呈正相关，绿泥石、伊利石含量与孔隙度呈负相关［12-13］；在川西须家河组和鄂尔多斯盆地华庆地区，高岭石和伊利石与物性之间无明显的相关性［8］，绿泥石含量与孔隙度呈正相关性［8，14-15］。可以发现，不同学者对不同地区矿物组分含量与储层孔隙度关系的研究所得出的结果存在较大的差异。研究结论差异性较大的原因既可能受区域背景的影响，更可能是受定量分析方法局限性的影响。

前人对储层物性的定量研究方法多为单因素（单一矿物）分析，而储层物性是受多因素（多种矿物）共同作用的结果。基于单因素分析的局限性，本文采用多元逐步线性回归法分析不同矿物含量对姬塬地区长6储层孔隙度的综合影响，以期通过矿物含量达到尽可能准确地预测储层孔隙度的目的。

1 地质背景

图1 研究区位置及鄂尔多斯盆地构造分区［16］Fig.1 Location of the study area and tectonic division of Ordos Basin

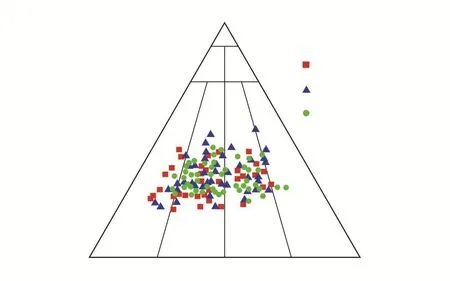
图2 姬塬地区长6储层的岩石类型［20］Ⅰ.石英砂岩；Ⅱ.长石石英砂岩；Ⅲ.岩屑石英砂岩；Ⅳ.长石砂岩；Ⅴ.岩屑长石砂岩；Ⅵ.长石岩屑砂岩；Ⅶ.岩屑砂岩Fig.2 Rock types of Chang 6 reservoir in Jiyuan area

姬塬地区位于鄂尔多斯盆地的中西部，横跨陕北斜坡、天环坳陷两大构造单元［16］（图 1）。长6油层组位于延长组中部，分为长63、长62、长61共3个小层，长63-长61沉积期整体上为一个湖退过程，湖平面下降，湖盆逐渐萎缩，形成一套水退型三角洲沉积，主要发育三角洲前缘亚相［17-20］。从长63沉积期开始，研究区主要发育来自北西方向的三角洲前缘碎屑沉积物；长62沉积期，由于盆地基底下降速率相对放缓，沉积物充填作用相对增强，来自西北和北东2个物源方向的碎屑物向半深湖方向推进，此时进入到三角洲平原沉积；至长61沉积期，来自北东方向物源的沉积物形成巨大的朵状三角洲沉积体系［21-22］。长6油层组岩性自底部的前三角洲亚相泥岩向上逐渐转变为三角洲前缘亚相粉砂岩与泥岩互层［23］。由于长6储层物性较低、具有较强的非均质性，导致含油砂体在纵、横向上的变化较大，严重制约了油气的开发效率［18，24］。

2 多元逐步线性回归原理

多元线性回归分析是一元线性回归分析的推广，在数理统计中，多元线性回归模型可表达为

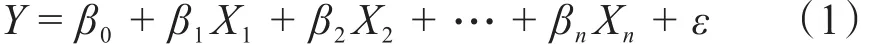
式中：Y为因变量，即观测量；Xi（i=1，2，…，n）为自变量，即影响观测量的因素；β0为回归常数，βi（i=1，2，…，n）为多元偏回归系数；ε为除去自变量后的随机误差（残差），且 ε服从 ε～ N（0，σ2）分布。

多元线性回归过程就是求解多元偏回归系数、检验评价回归方程并解释其合理性的过程。多元偏回归系数βi的求解通常采用最小二乘法，使得估计值Y^与观测值Y之间的残差在所有样本上的平方和（SSe）达到最小，即：

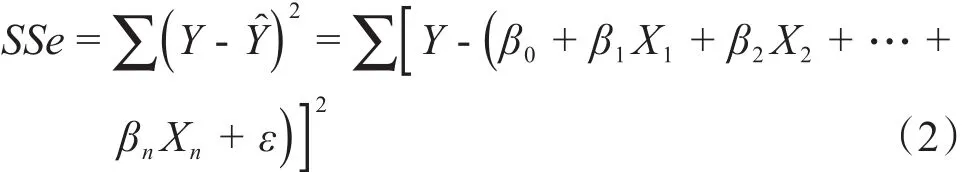
由高等微分学的原理可知，若使式（2）的值最小，必有 SSe 对于β0,β1,β2,…,βn的偏导数为 0，即

由式（3）可以建立关于β0和βi的n+1个方程，解出回归常数β0和偏回归系数βi，建立回归模型。同时，可以得到回归效果的相关参数，残差平方和（SSe）、回归平方和（SSr）、复相关系数（R）、F统计量（F）、t统计量（tj）：

式中：m为样品数，个；n为自变量数；cij为（XTX）-1矩阵中对应的元素。其中，复相关系数R是检验回归方程是否具有显著性的参数之一，当R＞R(0.05,m-n-1)时（显著性水平α＝0.05），说明多元回归方程具有较好的显著性［25］，R值越接近于1，说明回归效果越好［26］。F值是检验回归方程显著性的另一个参数，在多因素回归方程中，F检验相比于R检验更加准确，也更能说明方程的显著性，因此多用F检验法进行多元回归方程的检验［25］。t值用于检验回归系数的显著性，一般当t＞t(0.05,m-n-1)时，说明方程相应的回归系数具有较高的可信度。根据t值的大小依次剔除对应的不显著变量，当t＜t(0.05,m-n-1)时，说明相应的因素Xi对于Y的作用不显著，此时可以考虑将其剔除，然后用保留的因素再次回归，再次剔除对因变量Y影响不显著的因素Xi，如此重复，直至所有变量都能满足显著水平α=0.05的要求［27-28］，确定最终回归模型。

3 长6储层基本特征

对鄂尔多斯盆地姬塬地区长6储层岩石72口井519块薄片的统计观察并投点发现，其岩石类型主要为长石岩屑砂岩、岩屑长石砂岩，偶见长石砂岩（图2）。碎屑组分的体积分数为82.6%～83.8%，其中石英体积分数为29.3%～30.4%，长石体积分数为33.9%～36.2%，而岩屑和云母的体积分数分别为9.8%～12.1%，6.7%～8.1%，总体含量表现为长石＞石英＞岩屑＞云母［20］。在长6储层岩石岩屑成分中，变质岩岩屑体积分数为5.4%～6.7%，火成岩岩屑和沉积岩岩屑体积分数相差不大，分别为2.1%～2.6%，2.3%～2.8%（表1）。

519块薄片观察发现，长6砂岩储层孔隙类型主要为原生粒间孔［图3（a）］、长石溶蚀孔［图3（b）］，含少量的微裂缝和自生矿物晶间孔。通过薄片镜下观察以及X射线衍射（XRD）实验发现，研究区长6砂岩储层中胶结物、黏土矿物较为丰富（表2，3）。胶结物中碳酸盐矿物体积分数为3.30%～5.29%，铁方解石含量最高，体积分数为2.75%～4.60%；铁白云石和方解石含量次之，体积分数分别为0.22%～0.67%和0～0.26%；白云石体积分数仅为0.02%。硅质胶结分布较为广泛，但含量较低，体积分数为1.02%～1.25%。黏土矿物类型则以高岭石、绿泥石和伊利石等为主，其含量分布整体上表现为高岭石＞绿泥石＞伊利石（表3）。高岭石是姬塬地区长6储层中重要的黏土矿物类型，其主要以孔隙或喉道填隙物的方式充填残余粒间孔和长石溶蚀孔［图3（d），（e）］，其含量在长6 各小层中均较接近，体积分数为3.76%～3.98%。绿泥石是长6储层中含量仅次于高岭石的另一种重要的黏土矿物，主要以粒间孔填隙物的形式出现［图3（c）］。长6各亚油层组中绿泥石填隙物含量相差较小，其平均体积分数约为3.54%，在黏土矿物中占比为37.76%，在绿泥石中占比超过95%［20］。伊利石则主要呈丝缕状以搭桥式贯穿粒间孔中，集中出现时以网格状分布［图3（f）］，其含量较高岭石和绿泥石均低，体积分数为1.10%～1.73%。

表1 姬塬地区长6储层岩石成分［20］Table 1 Contents of rock composition of Chang 6 reservoir in Jiyuan area%

图3 姬塬地区长6储层的孔隙类型及其矿物分布特征（a）原生残留粒间孔，池 335 井，2 303.36 m，长 61；（b）长石溶蚀孔，76 井，2 338.63 m，长 62；（c）颗粒表面的薄层绿泥石膜、粒间绿泥石［20］，峰 11 井，2 369.17 m，长 61；（d）粒间高岭石，池 335 井，2 303.36 m，长 61；（e）粒间高岭石，盐 28 井，2 442.78 m，长 63；（f）粒间自生伊利石，盐 76 井，2 385.8 m，长 63Fig.3 Pore types and mineral occurrence characteristics of Chang 6 reservoir in Jiyuan area

长6储层中各种矿物组分含量较为丰富，石英脆性矿物可能对储层原生孔隙的保存具有一定的积极意义；长石矿物易被溶蚀，有利于局部次生孔隙的发育；相对较高的岩屑含量易造成储层被压实；不同的矿物胶结类型对孔隙的影响机制也有所不同。因此，通过多因子回归分析，能够提取出影响长6储层孔隙度的主要因子（矿物）、剔除次要影响因子、并确定主导因子之间的数学关系，建立孔隙度与矿物含量之间的关系模型，同时为储层孔隙度的预测提供理论算法。

4 回归结果分析

4.1 单因素分析矿物含量对储层物性的影响

根据长6储层岩石中主要的矿物组分类型，随机选取研究区岩石样品的相关数据做回归分析，分别建立储层孔隙度与单矿物含量之间的关系（图4）。

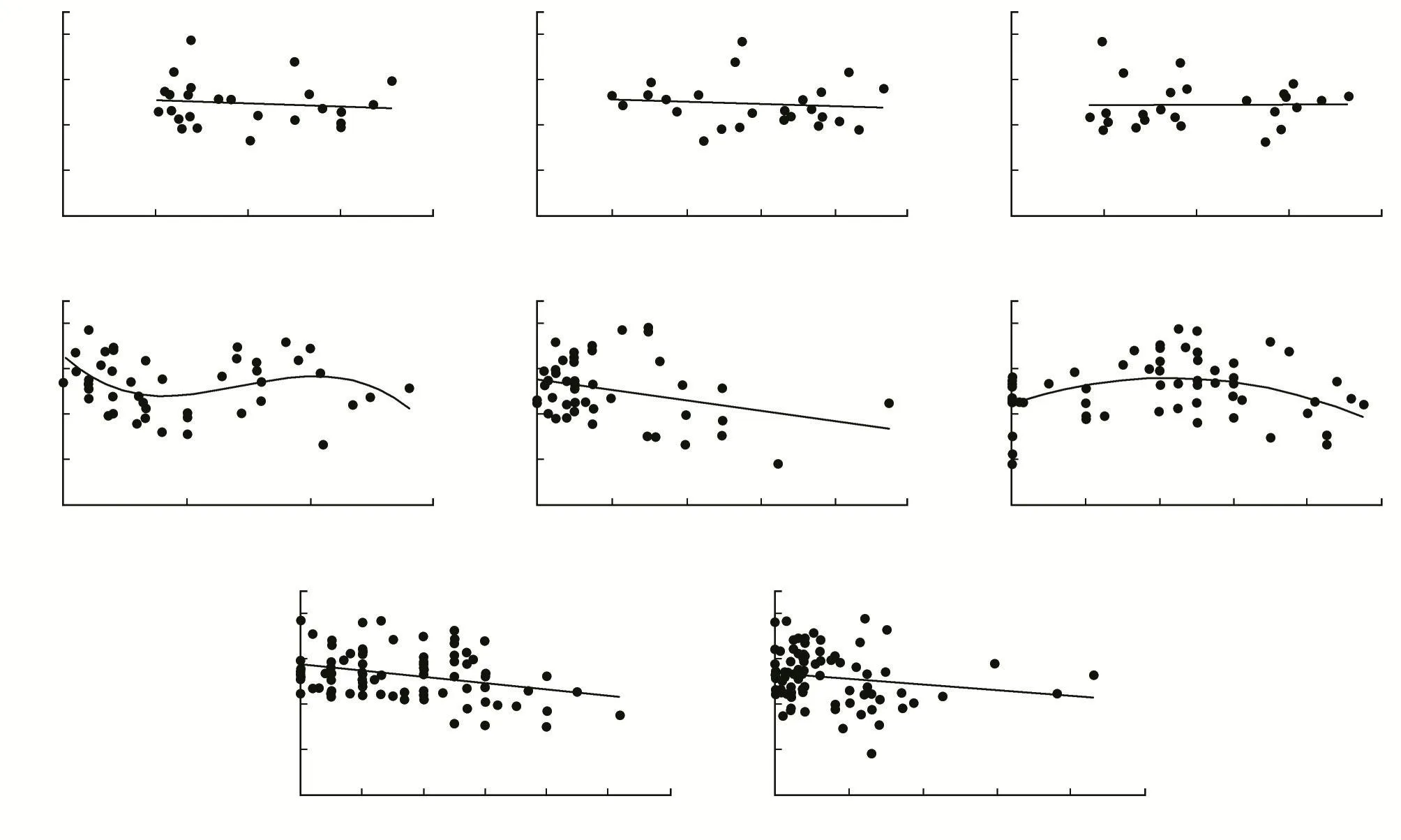
图4 长6储层孔隙度与矿物含量的关系Fig.4 Relationship between porosity and mineral content of Chang 6 reservoir

表2 姬塬地区长6储层胶结物含量［20］Table 2 Cement content of Chang 6 reservoir in Jiyuan area

表3 姬塬地区长6储层黏土矿物含量［20］Table 3 Clay mineral content of Chang 6 reservoir in Jiyuan area

孔隙度与石英、长石、岩屑含量之间无明显的相关性［图 4（a）—（c）］；孔隙度与绿泥石含量之间表现出较为复杂的分段关系［图4（d）］，孔隙度与伊利石含量呈较强的正相关［图4（e）］，而孔隙度随高岭石含量的增加有先增大后减小的趋势［图4（f）］；储层孔隙度与硅质含量和铁方解石含量均呈负相关性［图 4（g），（h）］。从图 4 中可以看出，虽然孔隙度与某些单矿物含量具有相关性［图4（d）—（h）］，但其相关性并不显著。且由一元回归方程的检验标准可知，只有当回归方程相关系数R大于临界相关系数R(α,m-n-1)时，回归方程才具有较高的可信度。查询相关系数临界值检验表得R2(0.05,24-1-1)=0.164。由图4中的8个回归方程相关系数可知，显然有R2＜R2(0.05,24-1-1)，因此其相关系数检验均未通过，说明孔隙度与单矿物含量之间可能并不存在较好的相关性。因为在地质作用过程中，各种矿物之间可能会发生相互转化，因此，储层孔隙度可能受多种矿物含量的共同影响。

4.2 多因素分析矿物含量对储层物性的影响

考虑到长6储层中单矿物含量与孔隙度之间可能并不存在明显的相关性，以及一元回归在储层物性分析中的局限性，拟进行多元逐步线性回归分析。以储层岩石的主要矿物：石英（x1）、长石（x2）、岩屑（x3）、绿泥石（x4）、伊利石（x5）、高岭石（x6）、硅质（x7）以及铁方解石（x8）等8种单矿物的含量为自变量，以储层孔隙度（y）为因变量进行多元回归分析。同时，为了在逐步线性回归过程中严格筛选出满足多元回归方程的自变量，选取自变量的显著性水平α=0.05（置信度为95%）作为评判标准，其回归过程与结果如表4所列。

从表4可以看出，共建立了孔隙度与8种矿物含量关系的回归方程模型。由模型1到模型8的建立过程采用的是反向多元逐步回归分析法，回归方程的复相关系数R由大逐渐变小，但基本都大于复相关系数R的临界检验值（除模型7与模型8外），说明回归方程均具有一定的显著性，因此无法通过R检验选择最佳的回归模型。

在多元回归过程中，综合F检验、t检验以及标准误差s分析认为，长6储层孔隙度最优回归方程为模型2：y=21.131-0.086 x2-0.113 x3-0.554 x4-0.370 x5-0.199 x6-0.659 x7-0.465 x8。从回归模型结果可以看出，长6储层孔隙度受多种矿物含量的共同影响，但绿泥石含量（x4）、伊利石含量（x5）、硅质含量（x7）及铁方解石含量（x8）的影响较大，而长石含量（x2）、岩屑含量（x3）和高岭石含量（x6）对长6储层物性影响较小，石英含量（x1）对储层孔隙度几乎没有影响。长石和高岭石含量对储层孔隙度的影响甚微、甚至没有影响，这可能与长石和高岭石之间的转化而体积几乎不变相关。Moncure等［29］通过理论计算也得出，1 mol的硅酸盐矿物溶蚀会产生0.66 mol的高岭石和0.30 mol的石英，因此对于一个相对封闭的成岩体系而言，长石、石英和高岭石三者之间存在某种自相关性，也就是说三者间的相互转化对孔隙度几乎没有影响。这与多元回归模型分析得出的结果具有良好的一致性。

表4 长6储层孔隙度与矿物含量逐步回归分析结果Table 4 Stepwise regression analysis of porosity and mineral content in Chang 6 reservoir

5 多元回归模型检验

为了验证回归模型2的可靠性，对建立的模型数据进行自检验（图5）分析，以及随机选取研究区另外13组长6储层岩石样品的相关数据进行他检验（表5、图6）分析。从图5回归模型的自检验可以看出，长6储层的实测孔隙度与模型计算孔隙度之间具有良好的协调性，仅个别数据点（样品3和样品12）偏离实际孔隙度较远，但均在误差允许的范围内，因此说明该回归模型具有一定的可信度。同时也表明，在准确建立了储层孔隙度多元回归模型的地区，也可通过相关因子（矿物含量）对未知孔隙度进行预测。

图5 长6储层孔隙度回归模型偏差自检验分析Fig.5 Self-verification analysis of deviation of porosity regression model of Chang 6 reservoir

为了进一步检验该回归模型的优越性和可预测性，随机选取的研究层位的13组岩石样品进行孔隙度预测（表5），发现实测原始孔隙度与模型预测孔隙度相对接近，说明回归模型对孔隙度均具有一定的预测能力。

为了更直观地反映模型的可靠性，将模型预测孔隙度与原始孔隙度进行相关性分析（图6）发现，模型2的预测值具有一定的可靠性。其中无截距回归方程的斜率反映了实测孔隙度数据与模型孔隙度数据之间的偏差，其值越接近于1，说明两者之间的相对精度越高。由图6可知，模型2的无截距回归方程的系数为0.995 3，基本接近于1，说明两者的相关程度较高。最优化回归方程的斜率同样反映了实测孔隙度数据与模型孔隙度数据之间的偏差，其截距的大小反映了偏差的大小，截距值越接近于0，说明偏差越小。从图6中的最优化回归方程可以看出，模型2的最优化回归方程斜率较大、截距为2.87，说明模型2的预测精度有2.87%的误差。同时，由最优化回归方程和无截距回归方程间的夹角可以看出，2种回归方程之间的夹角较小，说明模型2在孔隙度预测方面具有较高的可信度。

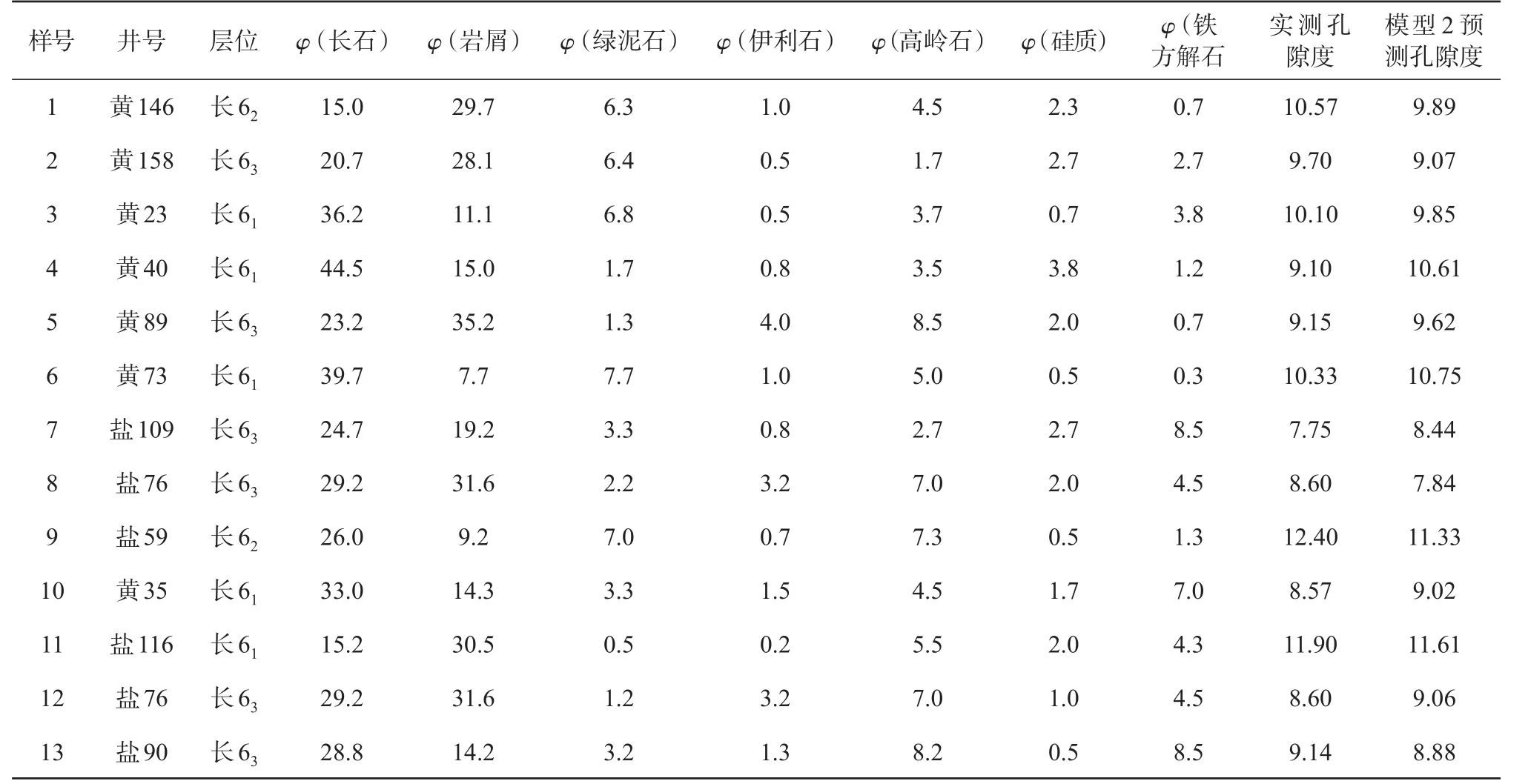
表5 长6储层孔隙度回归模型预测分析Table 5 Predictive analysis of porosity regression model of Chang 6 reservoir %

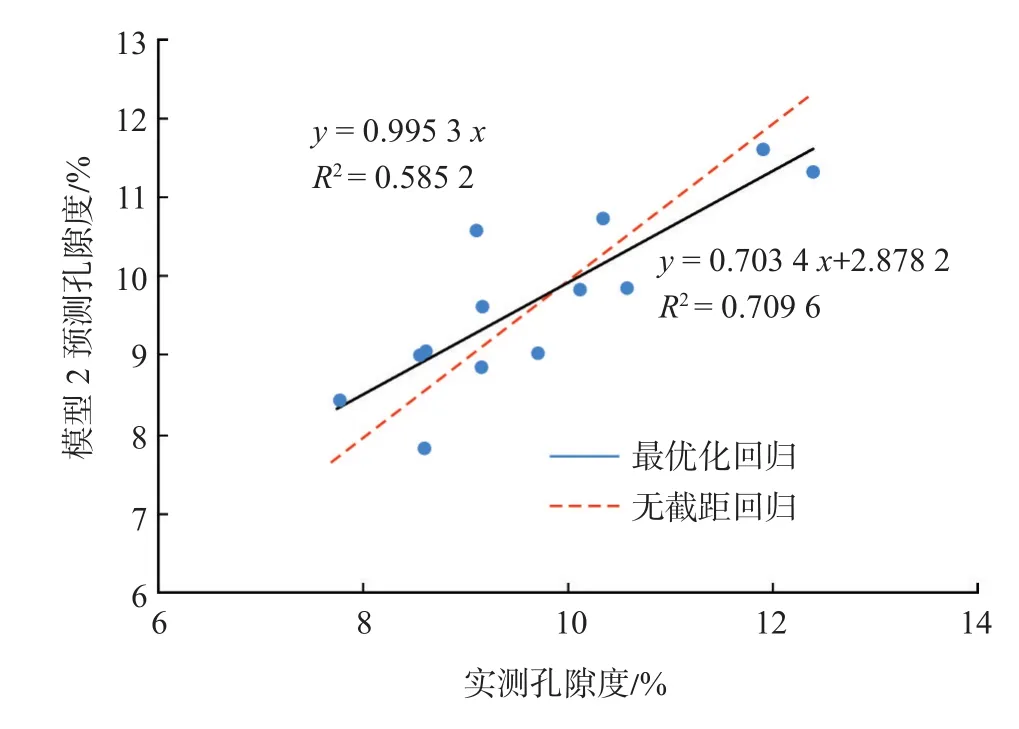
图6 长6储层孔隙度回归模型他检验分析Fig.6 Check analysis of porosity regression model of Chang 6 reservoir

6 结论

（1）通过多元逐步线性回归法，建立了长6砂岩储层孔隙度与矿物含量的定量模型：y=21.131-0.086 x2-0.113 x3-0.554 x4-0.370 x5-0.199 x6-0.659 x7-0.465 x8（模型2）。其储层孔隙度受多种矿物的共同影响，但绿泥石含量、伊利石含量、硅质含量及铁方解石含量的影响较大，而长石、岩屑和高岭石的含量对物性影响较小，石英含量对孔隙度几乎没有影响。

（2）基于逐步线性回归模型的建立过程与结果，长石、高岭石和石英含量对储层孔隙度的影响甚微，可能与这3种矿物间的相互转化而体积几乎不变有关。

（3）对最终回归模型进行自检验和他检验表明，实测孔隙度和模型预测（计算）孔隙度之间具有较好的拟合度，说明利用回归模型预测储层孔隙度具有一定的可靠性。同时也说明多元逐步线性回归法在分析多因素影响储层孔隙度的问题中具有良好的可行性。