丁坝长度对弯道水力特性影响的数值模拟研究

张 岩， 吴伊平， 崔鹏义， 黄远东， 张红武

(1.上海理工大学 环境与建筑学院， 上海 200093； 2.清华大学 水沙科学与水利水电工程国家重点实验室， 北京 100084)

1 研究背景

丁坝作为河流弯道整流的构筑物，一般修建于河流弯道的凹岸侧并向河道中心延伸，其中非淹没式丁坝最为普遍，其后可形成一定范围的束水区，凹凸两岸的部分水流在此得以混合，使弯道中水流流向和流速得以调整，从而减少对凹岸侧的冲击和淘刷，缓解凸岸侧泥沙易堆积的问题[1]。目前，对设置丁坝的河道中流体特性的分析研究可以通过数值计算及模型试验两类途径，大多聚焦在速度分布、水面特性、混流区涡流、丁坝水头损失等方面[2-7]。Kang[8]采用大涡模拟(LES)方法研究了直道水槽中的矩形丁坝周围的三维流场，并细致分析了丁坝前后的流体结构。薛海等[9]对弯道中水砂两相的河流流体进行了数值模拟研究，通过分析，肯定了下挑丁坝在改善河流流态中的作用效果。魏文礼等[10-11]运用大涡模拟结合VOF模型研究了90°弯道明渠中有无丁坝共4种工况下的水流水力特性，表明VOF模型用于研究弯道中环流现象效果良好。模型试验方面，郭维东等[12]设计了弯道水槽模型，借助测速仪器对设置丁坝后的流场形态进行了测试分析。Vaghefi等[13]、Nath等[14]在流态研究的基础上进一步通过试验研究了Froude数对弯道中丁坝冲刷效应的影响。

丁坝周围流动特性的研究多集中于直河道、直坝和T型坝等坝型，对弯道中丁坝的研究也多集中坝型和布置方式等方面。此外，弯道中丁坝长度直接关系到实际河道的治理，是必须考虑的问题。郑艳等[15]采用RNGk-ε模型，对设置有非淹没型丁坝的直河道进行了二维方向的数值模拟，探讨了运用RNGk-ε模型模拟丁坝河道流场的可行性，对坝长与尾流段尺寸的定量联系进行了探讨。本文基于前人的研究，选用 RNGk-ε湍流计算模型以及VOF气液两相流计算模型，对60°的河流弯道中未布设丁坝和布设0.15、0.25、0.35 m三个不同长度直丁坝进行数值模拟，采用魏文礼等[16]的相关试验数据进行模型验证，对比分析4种工况的流场结构和水面形态，为河流弯道治理和丁坝设计施工提供参考，具有理论和实际意义。

2 数值模型

2.1 计算区域和网格划分

本文研究的模型参考何婷婷等[17]研究中使用的模型尺寸和弯道角度，为了更好展现丁坝对其后尾流区流态的影响，将丁坝群简化为独立丁坝，采用的弯道模型如图1所示，弯道中心角为60°，凹岸侧弯角半径为1.6 m，凸岸侧弯角半径为0.8 m，河流过水截面为宽0.8 m，高0.4 m的矩形截面。弯道进出口各设4 m过渡直道与弯道相连。丁坝布设在弯道中心30°断面的凹岸，为非淹没式丁坝，高度为0.40 m，丁坝厚度为0.01 m，布设0.15、0.25、0.35 m三种长度的丁坝，尺寸如图1(c)所示，初始水深为0.25 m，其上部定义空气高度0.15 m，河道水槽断面如图1(a)。为更好地分析弯道中流速的变化，沿弯道行进方向每15°布置一个流速监测断面，共布置5个，如图1(b)所示。

使用GAMBIT2.4.6软件生成计算网格，采用混合网格，并在丁坝附近设置加密区，其余区域以丁坝为中心沿河道进出口方向划分为渐变网格，网格尺寸在丁坝坝头处取最小为0.001 25，相邻的网格按照1∶ 1.06 上下的增长率沿上下游河道递增，经独立验证的网格总数量在20万左右，坝长0.15 m工况下模型的计算网格设计见图2。

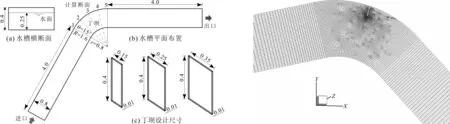
图1 研究采用的河流弯道丁坝物理模型(单位：m) 图2 网格划分

2.2 数值模拟方法

本文通过求解描述水流运动的三维Navier-Stocks方程、RNGk-ε湍流模型等，计算弯道中丁坝对于流速分布及流动特效的影响；河道中水流自由液面的水位变化运用VOF气液两相流模型来求解，液体和气体运动具有相同的速度场和压力场，气液两相流采用一组方程描述[18-19]。同时，在VOF的模型里，针对性加入了体积分数变量αq(第q相流体的体积分数)，表示所划分的网格里第q相流体的充盈情况。

第q相流体的体积分数αq的连续性方程为：

(1)

体积分数满足：

(2)

动量方程：

(3)

式中：xi、xj分别为i、j方向上的坐标；ui、uj分别为流体时均速度在i、j方向上的分量，m/s；p为压力，Pa；μt为湍流黏性系数，Pa·s；ρ为体积分数平均密度，kg/m3；μ分子黏性系数，Pa·s；gi为重力加速度在i方向上的分量，m/s2。

RNGk-ε方程[20]

k方程：

(4)

ε方程：

(5)

湍流黏性系数(湍流黏度)：

(6)

湍动能产生项：

(7)

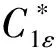
3 模拟结果及分析

3.1 不同工况流场结构分析

研究没有布置丁坝及丁坝长度分别为0.15、0.25、0.35 m共 4种工况(即工况1～4)的弯道水流特性。图3为不同工况弯道计算模型中距模型底部0.15 m高度平面上的流线图和速度云图，比较发现，在弯道流入端直道河流区段，流速及流线分布较为均匀，大致相对于河道中间轴对称分布。图3(a)所示，在无丁坝工况下，河流进入弯曲段河道, 在重力和离心力的合力效果下，靠近凹岸处静压增大，动压及流速减小，由于凹型河岸对河流的阻挡，水流对河岸产生冲击作用；靠近凸岸处上游静压减小，动压及流速增大，但凸岸下游易产生流动分离，造成泥沙淤积。另外，水流流经弯道后，流线出现弯曲、紊乱，研究发现，受弯道影响，弯道流出端的下游河道中凹岸附近的水流平均速度明显大于凸岸。弯道中布置丁坝后(图3(b)～3(d))，可以明显看出，坝后形成逆时针尾流区(平均流速较小)，随着坝体长度增长，尾流段的区域范围相应拓宽变长。弯道凹岸布置丁坝致使河岸收窄，过流断面减小，流速明显增加；并且当丁坝的长度变长，过流断面流线密度也相应变大，平均流速由约0.4 m/s(丁坝长0.15 m)增加到约0.6 m/s(丁坝长0.35 m)，靠近凸岸处流速较大。另外，在丁坝的挑流作用下，河流主要流体区段束紧，增加了坝后河道截面上水流速度的梯度，即速度的不均匀性，随着坝长增加，不均匀程度及影响范围进一步增加。当水流沿流出端河道区段继续流出，由于河流流体的耗散效应，水流速度变缓且缓慢恢复到均匀分散的状态，流线紊乱程度进一步降低。

3.2 弯道不同断面流速分布

图4为不同工况中弯道计算断面的速度分布云图，各计算断面位置参考图1。在弯道入流处截面，靠近中心线附近的流速最快，流速分布相对均匀；当流经弯道时，水流受到前方凹岸阻挡，使得近岸局部水压变大，两岸液面出现水面横比降的同时水流开始往凸岸流动，河流截面中出现横向环流；对比不同断面的速度分布情况可以观察到，最大速度随之往凸岸靠拢，由图4(a)可看出最大速度约0.45 m/s出现在弯道靠近凸岸壁面附近。观察单一横向断面流速分布，可以看到对于河道底端区域，其流速明显比顶部大。将图4(b)、4(c)、4(d)对比，发现弯道中布设丁坝后，水流流速分布情况明显发生改变，水流被丁坝阻挡后流向凸岸，断面3丁坝处最大流速由图4 (a)中的0.3 m/s增加到图4 (b)中0.35 m/s、图4 (c)中0.5 m/s和图4 (d)中0.6 m/s，即随着丁坝长度的增加而增大。河流流经转折弯曲河道，在重力以及离心力合力作用下，高流速区也开始由凸岸侧向河道中心偏移，对比不同工况中断面4、5的速度分布可看出，在丁坝后侧的尾流区，凹岸最大流速由0.3 m/s降低至0.1 m/s左右；凸岸流速增加的同时向凸岸偏移，且相对未布置丁坝的工况，偏移程度明显加大，两岸之间速度分布的不均匀性增加，而从断面5的速度分布可看出，随着水流向弯道下游流动，流速不均匀性减小，最大流速逐步往凸型河岸侧靠近。丁坝的布设打断了断面环流，其对流速分布的改变将有利于缓解水流对凹岸冲刷和凸岸泥沙淤积的现象，对工况2、3、4进行比较，随着丁坝长度的增加这种影响效果越明显。

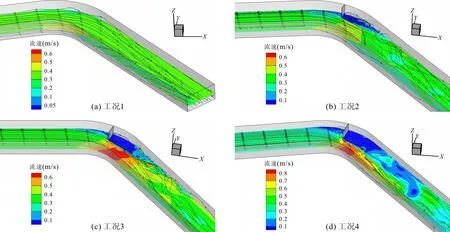
图3 不同工况下z = 0.15 m高度平面流速及流线云图

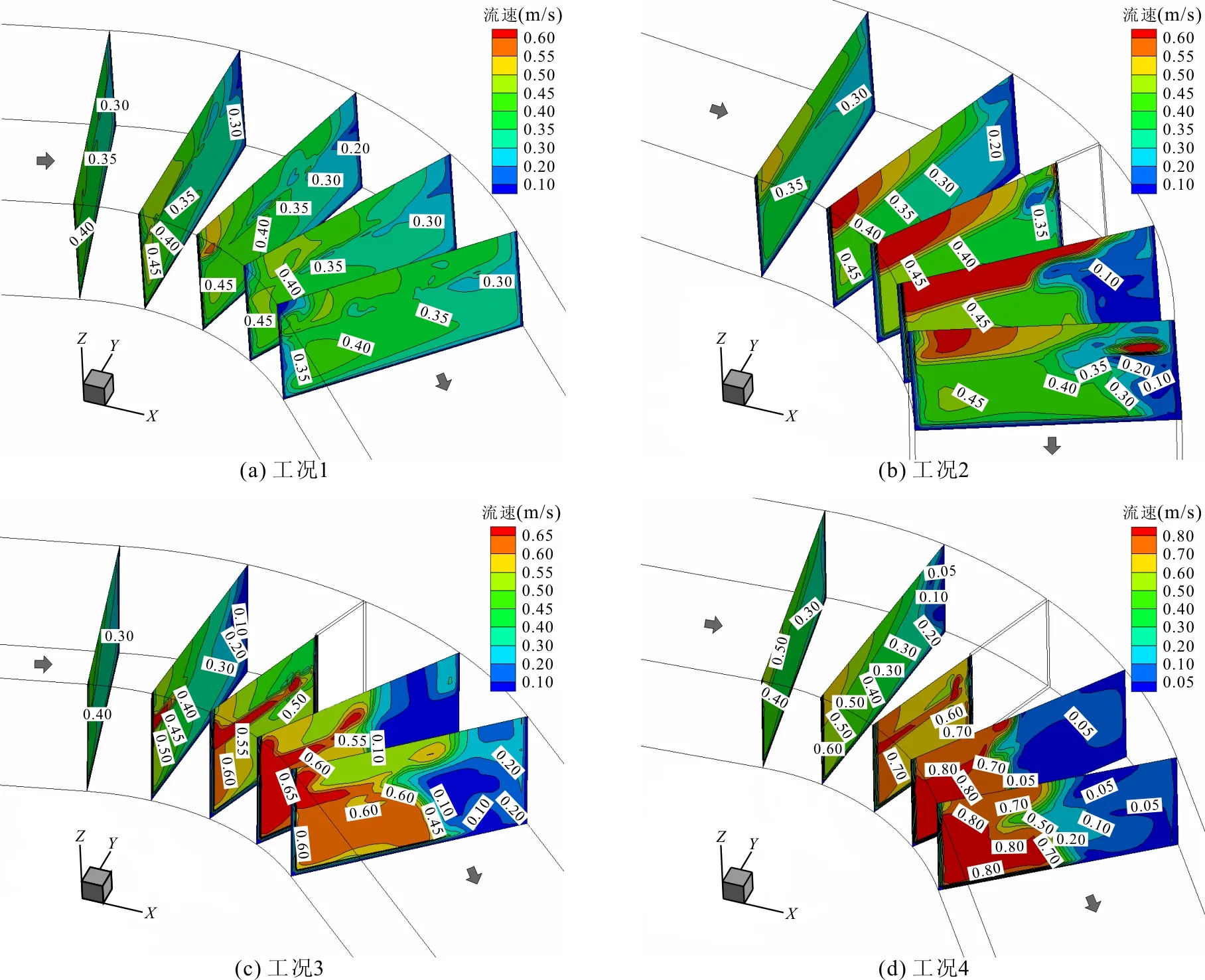
图4 不同工况各计算断面流速分布云图

3.3 湍动能及湍流黏度分布特性

湍动能大小表示水流脉动大小及混合程度的强弱，不同工况下距河道底部0.15m高度平面上湍动能分布如图5所示。工况1未设置丁坝时，湍动能分布较均匀，并且平均值较小，约0.0003 m2/s2；在弯道后凸岸附近湍动能相对较大，达到约0.001 m2/s2，这是由于在弯道凸岸处发生流动剧烈分离时所形成的旋涡在下游流场中对流扩散所致。从工况2、3和4可以看出，随着弯道丁坝长度的增加，坝后湍动能平均大小逐渐由约0.006 m2/s2增至约0.018 m2/s2，且影响范围也逐渐增大；另外，由于丁坝绕流的剧烈分离流动，湍动能分布还具有以下几个特点：(1)丁坝的布设使得坝后平均湍动能增加，其不均匀性也随之增加，坝后旋涡区流速较小，湍动能也相对较小；(2)在坝后沿流动分离及再附着的位置出现湍动能的最大值(最大值从坝长0.15 m的0.01 m2/s2到坝长0.35 m的0.018 m2/s2)，并且沿凸岸向下游扩散并减弱；(3)丁坝的布设大大增加了坝后凹岸附近湍动能水平。

湍流黏度μt的表达式如公式(6)所示。对于水固两相流，湍流黏度μt控制着悬移质固体扩散。图6表示不同工况下距模型底部0.15 m高度平面湍流黏度的分布情况。可以看出，对于未布设丁坝的弯道(图6(a))，在弯道前的直河道内μt分布比较均匀，大小约为0.04 m2/s3；当流经弯道时，由于过流断面的变化及离心力的作用，水流横向流速梯度和紊动程度明显增加，湍流黏度在弯道入口处增强，约为0.1 m2/s3。流过转折弯曲河段，在离心力影响下，靠近凸岸和下游河道中心均可看到湍流黏度较强区域，大小约为0.16 m2/s3，这与上文湍动能的分布规律类似。

对图6(b)、6(c)、6(d)进行对比，发现布设丁坝后，随着尾流区域回流旋涡的产生，旋涡处湍流黏度均值超过0.2 m2/s3，且最大值出现在坝后漩涡中心处，湍流黏度的分布情况也反映了丁坝后涡流的运动变化情况；丁坝的长度逐渐增加，其后尾流区湍流强度不断增大，旋涡发展变大，分布更加密集，平均湍流黏度也不断增加至超过0.3 m2/s3。

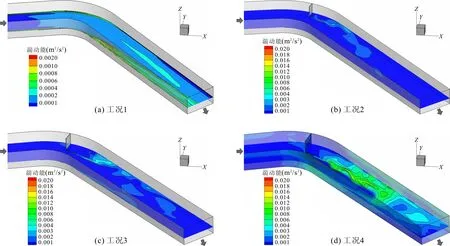
图5 不同工况水流湍动能分布云图

3.4 水面形态分析

水面横比降是带有弯曲段河道的重要流态参数。弯曲段水流在重力及离心力的合力影响下，凹岸局部压强增大引起凹岸侧液面提升、凸岸侧液面下移。

本文参考张红武等[21]和孙一等[22]的相关研究，弯道水面横比降计算采用的公式如下：

(8)

式中：n为计算断面标号，详见图1；Za、Zb为弯道凹岸侧、凸岸侧计算水位值，m；B为弯道河段宽度值,m。计算得到不同工况各计算断面的水面横比降及体积分数值如图7所示。由图7(a)可得，对于未布置丁坝的河流弯道，在进入弯道的起始阶段，横比降增加较为迅速，从断面1到断面2水面横比降由0.0081增至0.0116，之后呈波动变化趋势。对比图7(b)、7(c)、7(d)可以发现，弯道中布置丁坝后，在进入弯道阶段的横比降仍然呈上升趋势；在坝前位置，坝体阻挡了水流的惯性运动，水面横比降迅速提升；在丁坝位置处的断面3，水流流经丁坝，迅速向丁坝后侧收缩，水面横比降减小；进入丁坝后部的尾流区，水流形成回流漩涡，凹岸水位相对下降，而凸岸由于横向环流的作用，水位提升，造成水流在流经丁坝后横比降呈迅速减小趋势，同时由于旋涡的存在，凹岸水位呈现一定波动；弯道出口后，水流缓慢恢复平稳状态。水面横比降变化趋势(即在坝前和坝后均有一个极大值)与魏文礼等[16]进行的弯道试验研究变化趋势一致，进一步验证了模拟结果的可靠性。

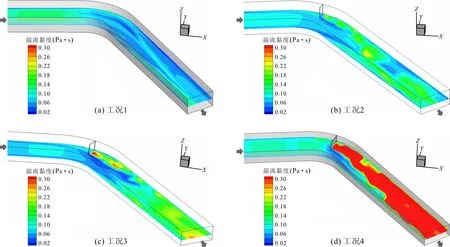
图6 不同工况水流湍流黏度分布云图

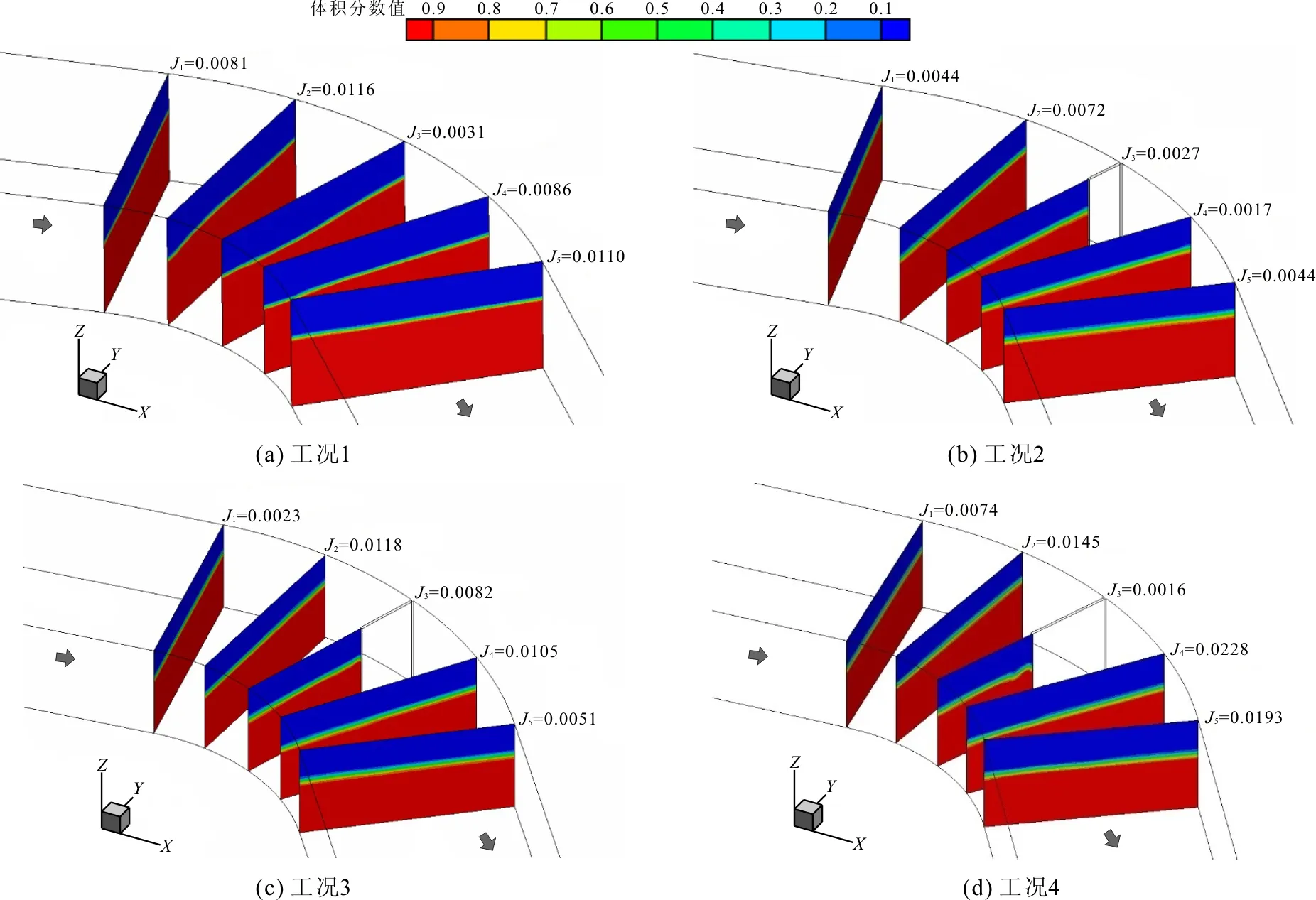
图7 不同工况各计算断面水面横比降云图

4 结果与讨论

本文采用RNGk-ε湍流模型和VOF模型，分析了60°弯道内丁坝长度对水流特性的影响，可以得到以下结论：

(1)当水流流经弯道时，受到重力及离心力的共同作用，水流冲刷阻水的凹岸，导致凹岸区域局部静压增大且流速减小；凸岸区域流速明显大于凹岸，受离心力作用水流从上游凸岸产生流动分离，导致在凸岸下游易产生泥沙淤积。

(2)坝体阻挡了水流的惯性运动，破坏了断面横向环流，减缓了凹岸受到的冲击；丁坝长度的增加使得丁坝前水面横比降增大，水流绕过丁坝向其后收缩，形成了明显的逆时针大旋涡，同时水面横降比得到调节。

(3)随着丁坝长度的增加，丁坝后部回流区尺度随之增大，湍动能及湍流黏度作用强度及范围随之增大，湍动能的最大值出现于坝后流动分离河段，湍流黏度的最大值出现在坝后旋涡中心附近。