传热结构自适应成长法的敏度过滤技术研究

季懿栋，丁晓红

（上海理工大学 机械工程学院，上海 200093）

随着电子产品的功率增大、体积减小，工作时积聚的热量急剧增加，寻找一种合适的散热方式变得尤为重要。自然对流等传统散热方式的效率低，无法满足当前散热要求。而强制对流等方法虽然效率高但需要较大空间，难以应用于小空间电子产品[1-3]。一种有效的方法是采用能量疏导方式。所谓能量疏导就是将一定体积的高导热系数材料敷设于元器件基板表面或直接嵌入其内部形成传热通道，从而将工作时产生的热量高效传导至外部环境[4]。

合理的传热通道布局设计，可以有效地提高传热效率。早期传热通道布局的设计依赖于经验或直觉，设计结果不仅传热效率低且难以应对实际工程中复杂的热边界条件。以热阻最小为目标，Bejan[5]提出构形理论并设计得到树形传热通道。此后随着拓扑优化技术发展，以SIMP（solid isotropic material with penalization）插值的变密度法[6]、渐进结构优化法（evolutionary structural optimization，ESO）[7]，以及水平集方法[8]为代表的各类结构拓扑优化方法都被应用于设计传热通道的分布。上述方法获得的设计结果的传热效率高且形态皆与树形结构相类似，然而，设计结果中存在棋盘格现象，灰度单元较多，过多细小分支，且不便于制造。Ding等[9]通过对自然界分支系统成长机理的研究，提出了自适应成长法，并应用于传热通道的布局设计中[10]。由该方法得到的传热通道布局简单清晰，但在较复杂热边界条件下，会出现平行通道分支。

本文提出一种包含敏度过滤的两层顺序优化生长新策略，从而解决了现有问题。通过不同热边界条件的典型二维散热问题，验证提出方法的有效性，并比较各类敏度过滤技术在该方法中的适用性。

1 传热结构自适应成长法

1.1 自适应成长法原理

自然界的生物分支结构，例如，植物根系，在生长过程中，其根系在自身遗传因素影响及重力性、向触性、趋水性等限制[11]下，自适应成长并尽可能多地将土壤中的营养物质传输到根部。如图1所示，植物根系在趋水性的作用下，根系向水源所在方向生长，以获得最大的生长动力，同时生长过程中长出大量分支。具有高导热系数的传热通道的功能是在不同边界条件的限制下，将基体中的热量尽可能多地传导至外部环境。图1中传热通道由风扇延展至具有高热量的CPU区域。由此可见，传热结构与自然生物分支结构在功能及形态上较为相似。因此，传热结构优化设计应如同自然分支结构一般可在给定的目标下，按照某种设计准则，向最优方向生长。传热结构自适应成长法中，通过在设计域内引入固定结构形式的基结构，将高自由度的材料拓扑优化问题转变为低自由度的以截面积为设计变量的拓扑优化问题。建立合适的数学模型并推导针对截面积变化的迭代公式，对截面积进行优化。优化后的几何形态即为用高导热材料铺设的传热通道的分布形态。

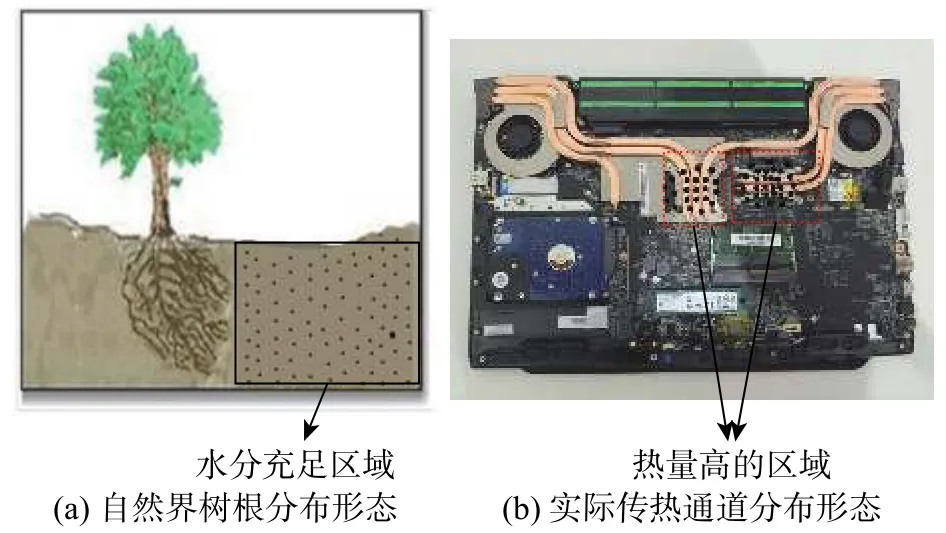
图1 自然界与实际通道的分布形态Fig.1 Distribution morphology in nature and practical channel

1.2 自适应法的数学模型及最优准则迭代公式推导

考虑如图2所示的典型稳态热传导问题的传热结构拓扑优化设计，该问题可以描述为：在具有内热源的设计域内，给定绝热边界和散热边界，以散热弱度最小为目标函数，在给定高导热材料体积的约束下，寻求各传热结构分支截面积的最佳分布。

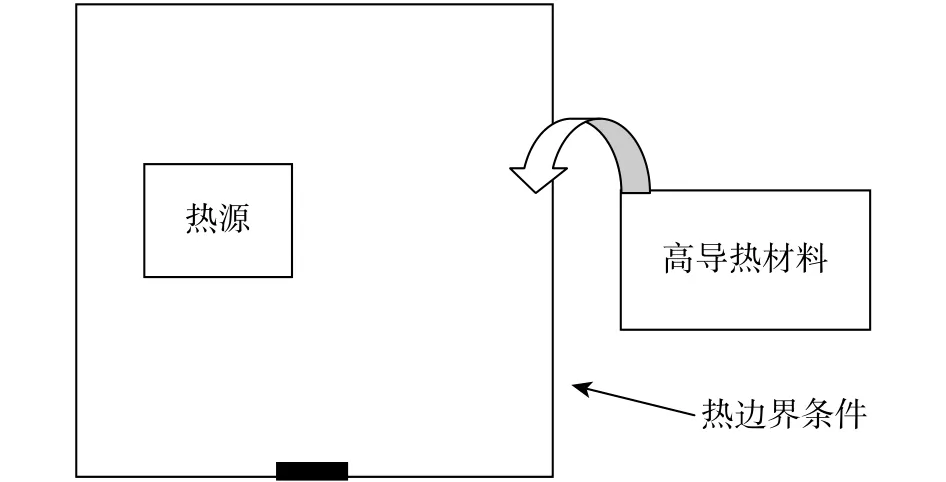
在传热结构自适应拓扑优化方法中通过引入设计变量xi与分支的截面积相关联。截面积Ai与相应的设计变量之间的插值关系可以表示为

式中：Amax，Amin分别为分支截面积的最大值和最小值；p为插值模型的惩罚系数。

通过该插值模型可以将设计变量Ai转化为设计变量xi。其中，p不同取值下的插值模型如图3所示。可以看出，当惩罚系数时，该插值模型对变量Ai具有惩罚效果，且p取值越大，惩罚效果也越明显。

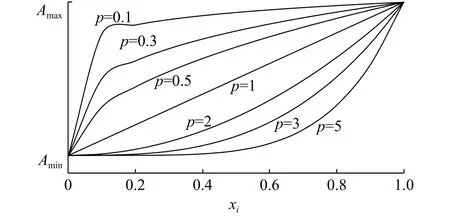
图3 插值模型Fig.3 Interpolation model

在引入变量xi后，稳态热传导问题中的传热结构拓扑优化设计的数学模型可表示为

式中：xi为各分支的截面积Ai对应的设计变量；n为基结构个数；T为各节点温度矢量；P为节点热载荷矢量；V为优化后基结构总体积；vi为第i个单元体积；q为体积约束因子；V0为初始体积；xmax，xmin分别为设计变量的上限与下限。

采用最优准则法进行求解，由式（2）构造拉格朗日函数。当该拉格朗日函数满足一定条件时[12]，目标函数f（x）可取最小值。综合考虑设计变量上下限的值、体积约束条件以及热刚度矩阵的对称性，最终得到优化迭代公式：

式中：K为导热系数比；为体积约束条件的拉格朗日乘子；ri为第i个单元的热耗散值；为迭代次数；α为阻尼系数。

2 改进的传热结构自适应成长法

2.1 敏度过滤技术

目前，传热结构自适应成长法得到的传热通道布局中存在一定数量的平行通道，而产生平行通道是算法数值不稳定的一种表现。解决该问题的方法有高阶单元法[13]、周长约束法[14]和敏度过滤方法[15]等。其中，敏度过滤更具有实际参考意义[16]。

敏度过滤技术[17]是利用过滤范围内所有单元的敏度信息修正中心单元的敏度信息，即采用过滤半径范围内各单元敏度的加权平均值代替中心单元的敏度值，从而避免数值不稳定现象的发生。由 Sigmund在 SIMP[18]中提出的敏度过滤（SIMP过滤）中首先定义某一单元邻域的集合

式中：单元e为中心单元；单元i为单元e邻域中的一个单元；xi与xe分别为单元i与单元e的空间中心位置；r为过滤半径。

SIMP过滤公式为

为了使拓扑优化结果的边界进一步清晰，Borrvall提出了修正的敏度过滤（Borrvall过滤）[19]，其公式为

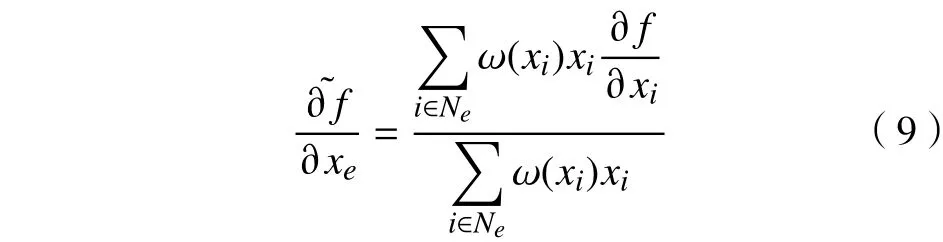
杜义贤等[19]借鉴标准粒子群优化算法（PSO）中的粒子状态更新方法，提出了一种改进的敏度过滤技术（PSO过滤），即根据单元及其相邻单元中敏度的极大值和极小值来修正该单元的敏度，公式为

式中：ω 为惯性权重；c1，c2为学习因子，为正常数。

ω控制着原单元敏度值对当前修正值的影响程度，学习因子反映了单元向邻域中2个敏度极值学习的程度。杜义贤等[19]通过数值算例验证认为，当学习因子而惯性权重时，PSO过滤方法能够得到更好的效果。

为了克服敏度过滤方法带来的边界扩散问题，龙凯等[20]提出了考虑密度梯度信息的敏度过滤方法（Density过滤），该方法在原有敏度过滤表达式中增加了密度梯度修正权函数项，来获取具有清晰边界的拓扑优化结果，其公式为

式中：λ为考虑密度梯度信息的修正权函数；β为密度界限值。

大量数值算例结果表明，在本文研究的问题中，为取得较为良好的拓扑优化结果，密度界限值β=0.2。

2.2 改进的传热结构自适应成长法流程

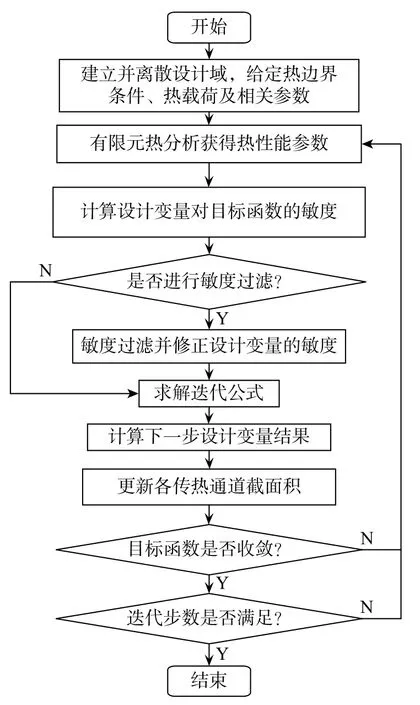
原成长法得到的设计结果形态清晰,但存在平行通道，针对这一问题提出了一种两层顺序优化的传热结构自适应成长法，第一层优化采用包含敏度过滤的自适应成长法，优化迭代收敛后所得的结果作为第二层优化的初始解；第二层优化采用无敏度过滤的自适应成长法继续生长，直至结果收敛。改进的传热结构自适应成长法流程如图4所示。

首先定义设计域，并建立基结构。根据具体工况，为设计域施加相应热边界条件以及热载荷，并给出成长参数及敏度过滤参数。

通过对设计域进行有限元热分析，获取设计域内各类热性能结果，从而为后续迭代作准备。计算各设计变量对目标函数的敏度值，并通过敏度过滤修正各设计变量相应的敏度值。随后采用求解得到的迭代公式计算出下一步的设计变量结果，并根据设计变量更新相应分支的截面积。重复以上步骤直到目标函数收敛后，去除敏度过滤这一步骤，并重复以上其他步骤。当相邻两次迭代的目标函数值的差值小于收敛容差且迭代步数达到要求，认为结果收敛。

3典型数值算例

3.1 底边单点热沉算例

考虑如图5所示的底边单点热沉同时内部均匀生热的数值算例问题。设计域Ωs为0.1 m×0.1 m正方形。设计域内部均匀生热，其生热率为6×104W/m3。在设计域的底边中部有散热边界，长度L=0.01 m，温度T0=0℃，其余边界绝热。覆盖设计域的材料为低导热材料，并用白色表示。相关成长参数以及敏度过滤相关参数如表1及表2所示。分别采用两层顺序优化的改进成长法与原成长法求解。

原成长法得到的设计结果如图6（a）所示，迭代历程如图6（b）所示。迭代收敛后，获得的传热通道分布形态大致呈“山”字形，传热通道的底部存在分别向两侧延展的传热通道分支。得到的传热通道的分布中，中央传热通道的顶部存在有三根平行的传热通道分支，同时两侧传热通道的顶端也各分布有三根高度依次递减的平行通道分支。

表1 成长相关参数Tab.1 Relevant parameters for growth

表2 敏度过滤参数Tab.2 Parameter for sensitivity filtering

加入不同敏度过滤的改进成长法得到的传热通道分布形态分别如图 7（a），7（b），7（c）以及7（d）所示。迭代历程如图7（e）所示，迭代均收敛。使用SIMP过滤的改进成长法得到的传热通道形态为“V”字形，底部有向两侧延展的传热通道分支。Borrvall过滤得到的传热通道中存在小部分未与传热通道相连接的传热通道分支。Density过滤得到的分布大致与SIMP过滤结果相似，其中央还生长有两根竖直传热通道分支。由PSO过滤得到的传热通道分布形态为“山”字形。观察不同结果可以发现，Density过滤所取得的拓扑形态中的平行通道数量最少，结构最清晰。由图7（e）所示的迭代历程可以发现，与其他三类敏度过滤结果以及原成长法结果相比，Density过滤能取得最小的散热弱度。Density过滤取得的散热弱度为27 055，而原成长法散热弱度为28 756。

图6 无敏度过滤的传热结构自适应成长法设计结果(1)Fig.6 Design result of the adaptive growth method without sensitivity filtering(1)

从最高温度、平均温度以及温度标准差三方面对比评价无过滤成长法与改进成长法得到的设计结果，如图8所示，改进成长法的温度性能大部分优于原成长法的温度性能。其中，加入Density过滤的改进成长法所得到的温度性能均最低，分别为68，42和16℃，比原成长法结果分别降低了18%，12%和5.9%。

3.2 中心单点热沉算例

考虑中心单点热沉同时内部均匀生热的数值算例问题。如图9所示，热沉为一正方形，长宽均为L=10 mm。其余边界条件与优化参数均与底边单点热沉算例一致。分别采用改进成长法与原成长法求解该问题。

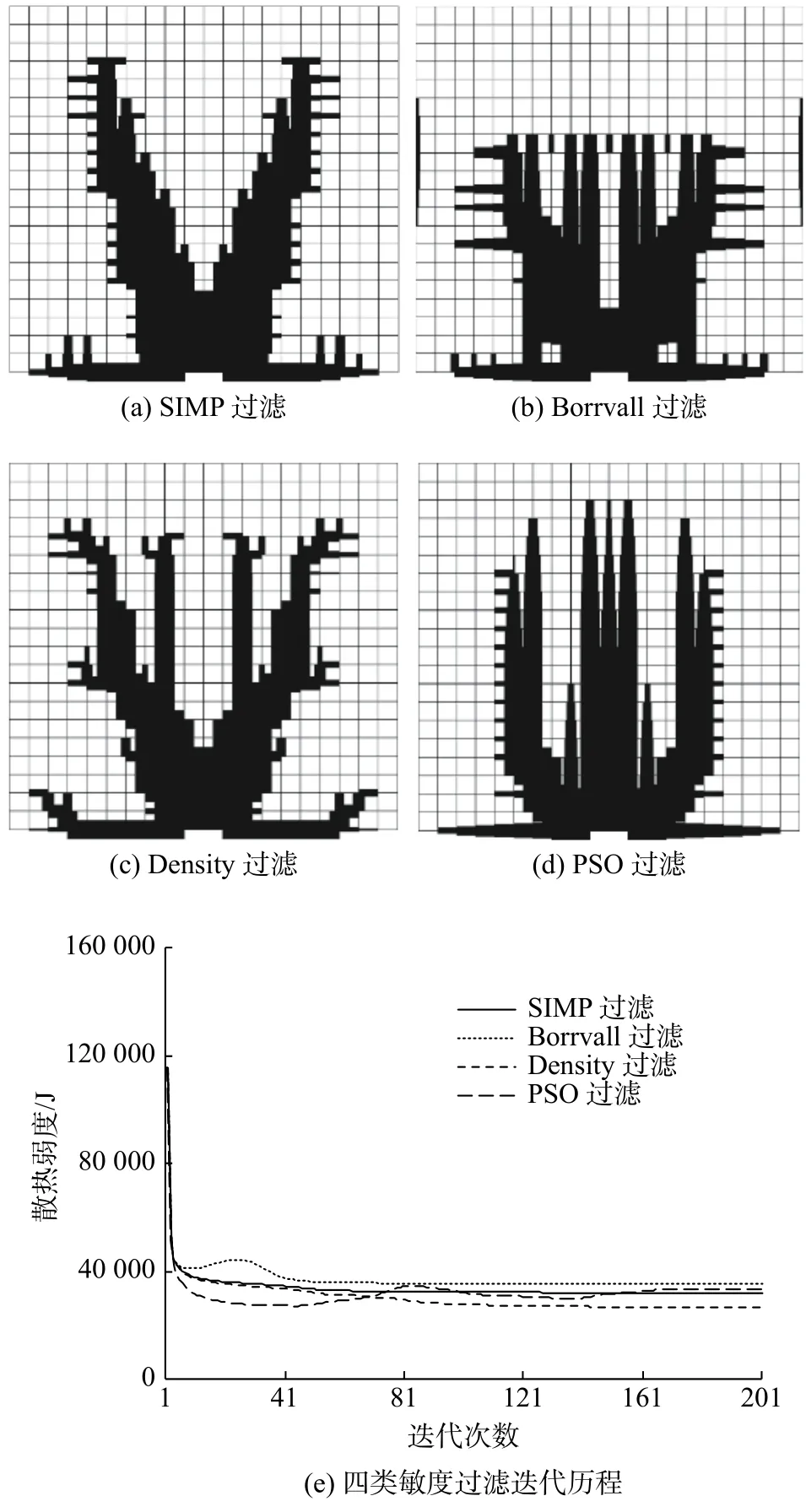
图8 改进成长法与原成长法设计结果的温度性能对比(1)Fig.8 Comparison of temperature performances obtained by the improved adaptive growth method and original adaptive growth method(1)

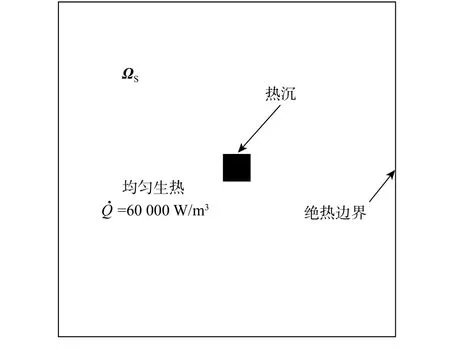
图9 中心单点热沉算例模型Fig.9 Design problem about single heat sink at the center of design domain

原成长法获得的传热通道的分布形态如图10（a）所示，迭代历程如图10（b）所示。传热通道的分布呈“米”字形，以热沉为圆心，垂直和竖直方向以及对角线方向都有传热通道存在。在垂直以及竖直方向的传热通道分支各分布有三根平行的传热通道。

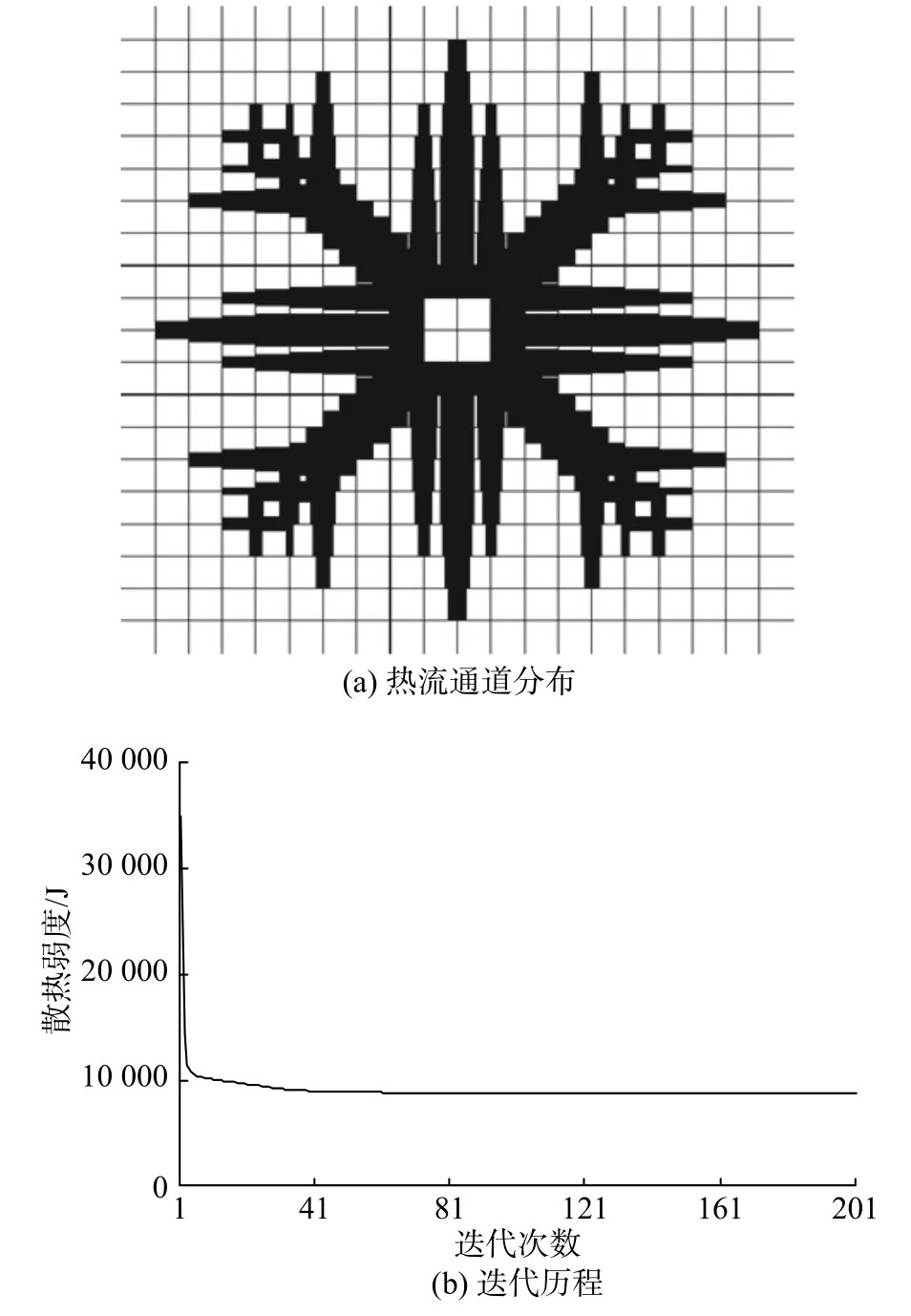
图10 原成长法设计结果(2)Fig.10 Design result of the original adaptive growth method(2)

加入不同敏度过滤的改进成长法得到的传热通道分布形态如图 11（a），11（b），11（c）以及11（d）所示，迭代历程如图11（e）所示，迭代均收敛。四类敏度过滤下的传热通道分布较为相似，呈“米”字形分布。以热沉为圆心，垂直和竖直方向以及对角线方向都有传热通道存在。加入Density过滤得到的传热通道分布中的平行通道数量最少，没有出现大量长分支，且分布清晰、边界不模糊。其余结果中均有较多平行通道。由图11（e）迭代历程发现，Density过滤取得的散热弱度比其他过滤方法及原成长法更小。Density过滤取得的散热弱度为8 080，而原成长法散热弱度则为8778。

图11 改进成长法设计结果(2)Fig.11 Design result of the improved adaptive growth method(2)

三类温度性能对比如图12所示，改进成长法得到的三类温度性能大部分优于原成长法的三类温度性能。其中，加入Density过滤的改进成长法得到的三类温度性能最低，分别为26，13和5.9℃，比无过滤情况分别降低了13%，7.1%和18%。

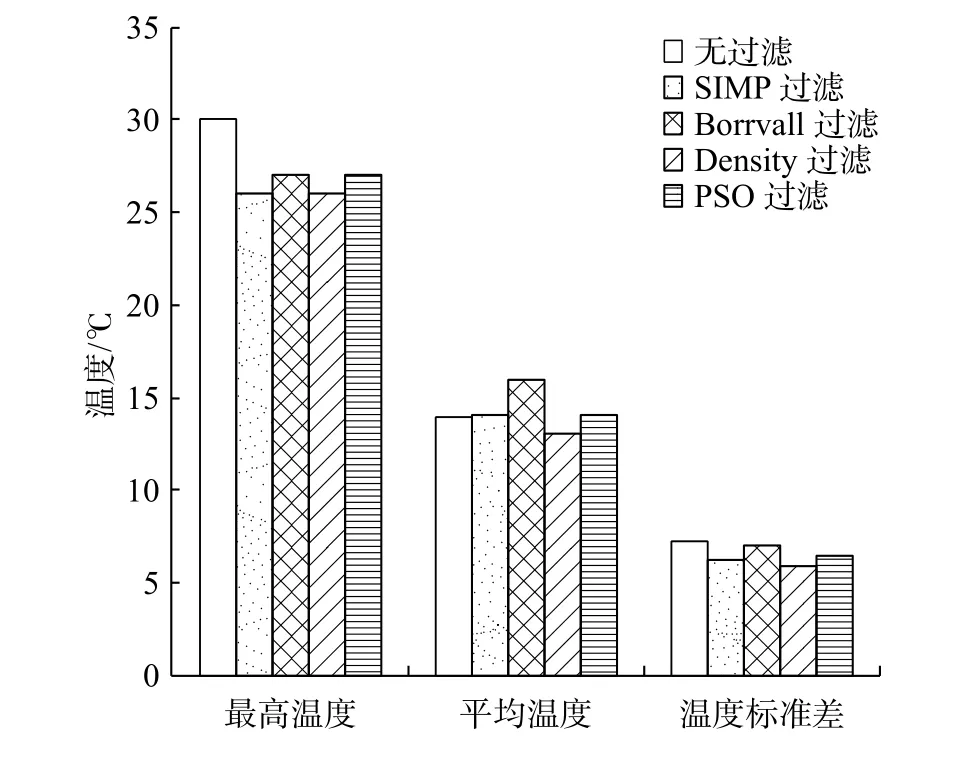
图12 改进成长法与原成长法设计结果的温度性能对比(2)Fig.12 Comparison of temperature performances obtained by the improved adaptive growth method and original adaptive growth method(2)

3.3 底边单点热沉不均匀生热算例

考虑底边单点热沉同时内部不均匀生热的数值算例问题。如图13所示，灰色部分表示生热区区域。其余边界条件与参数仍与底边单点热沉算例一致。分别采用两种方法求解该问题。

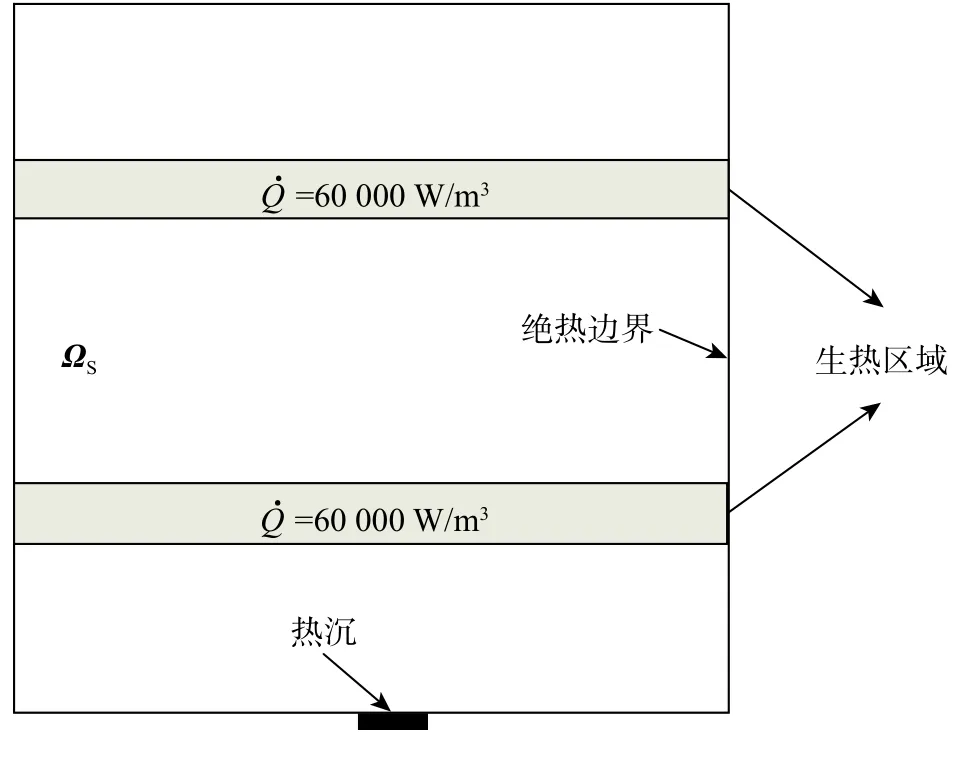
图13 底边单点热沉不均匀生热模型Fig.13 Design problem about single heat sink at the buttom of design domain

原成长法得到传热通道分布形态如图14（a）所示，迭代收敛情况如图14（b）所示。获得的传热通道分布形态呈“山”字形，存在平行传热通道分支与独立传热通道分支。

图14 原成长法设计结果(3)Fig.14 Design result of the original adaptive growth method(3)

改进成长法的设计结果如图 15（a），15（b），15（c）以及 15（d）所示，迭代历程如图 15（e）所示。可以发现，使用不同敏度过滤的改进成长法得到的传热通道分布均较为相似，大致呈“业”字形。在虚线框处，即有生热区域均有斜向传热通道分支出现。SIMP过滤与Density得到的结果在传热通道边界处均有一定数量的细小平行通道分支。其中，Density过滤得到的拓扑形态中虽然仍有一定数量的平行通道，但与其他3种过滤方法相比，图15（c）中平行通道最少。其他方法中平行通道较多且存在独立分支。由图15（e）迭代历程发现，Density过滤取得的散热弱度最小。Density过滤取得的散热弱度为2 398，而原成长法散热弱度则为 2 969。

改进成长法的三类温度性能与原成长法对比如图16所示，均优于原成长法设计结果。其中，加入Density过滤的改进成长法的设计结果的温度性能最佳，分别为21，13和5.1℃，比无过滤情况分别降低了22%，13%和12%。

3.4 讨 论

在以上3个数值算例中，加入Density过滤的改进成长法在拓扑形态、目标函数以及温度性能均取得最优的结果，这是由于在Density过滤中引入了密度修正权函数。在传热通道分布内部，即密度分布较为接近的区域中，Density过滤与SIMP过滤一致。而在分布的边界处，即密度分布变化较大的区域，修正权函数能消除密度较大单元的敏度对密度非常小单元的敏度修改，从而避免边界不断扩散，在SIMP过滤与Borrvall过滤中均无法避免这一问题。而在PSO过滤中，只考虑邻域中最大敏度与最小敏度对当前敏度的影响。因此，在本文研究的3个数值算例中，Density过滤能得到更为合理的传热通道分布，平行通道少且边界清晰。

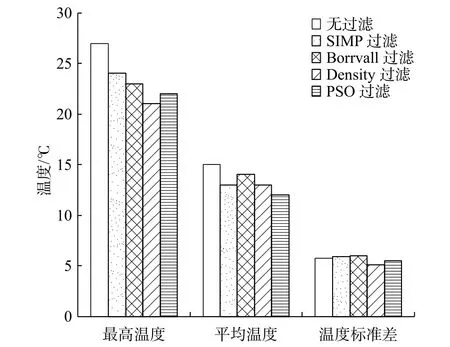
图16 改进成长法与原成长法设计结果的温度性能对比(3)Fig.16 Comparison of temperature performances obtained by the improved adaptive growth method and original adaptive growth method(3)

在3个数值算例中，对比了改进成长法与原成长法的设计结果，但未与只使用过滤的原成长法进行对比。为了进一步验证改进成长法，选取加入Density过滤的改进成长法与加入Density过滤的原成长法，对比分析两者的设计结果，对比数据如表3所示。

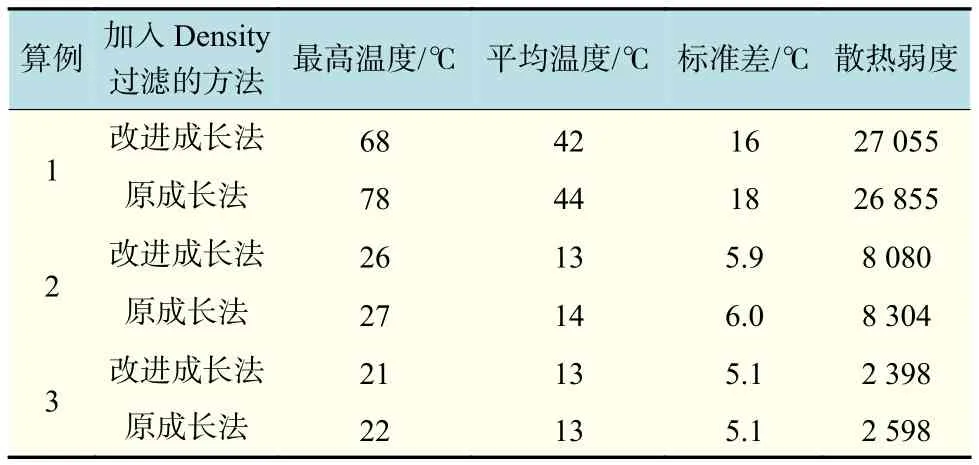
表3 改进成长法与原成长法对比Tab.3 Comparison between the improved adaptive growth method and original adaptive growth method

通过表3中的数据对比可以发现，加入Density过滤的改进成长法与加入Density过滤的原成长法在不同算例中不同热性能参数上十分接近，整体而言，改进成长法略优于原成长法。选择第一个数值算例，对比两种方法的拓扑形态。

图17（a）为加入Density过滤的改进成长法所得拓扑形态，而图17（b）为加入Density过滤的原成长法拓扑形态。两者的拓扑形态十分相似，其中，改进成长法的拓扑形态边界十分清晰，而原成长法的拓扑形态边界非常模糊。

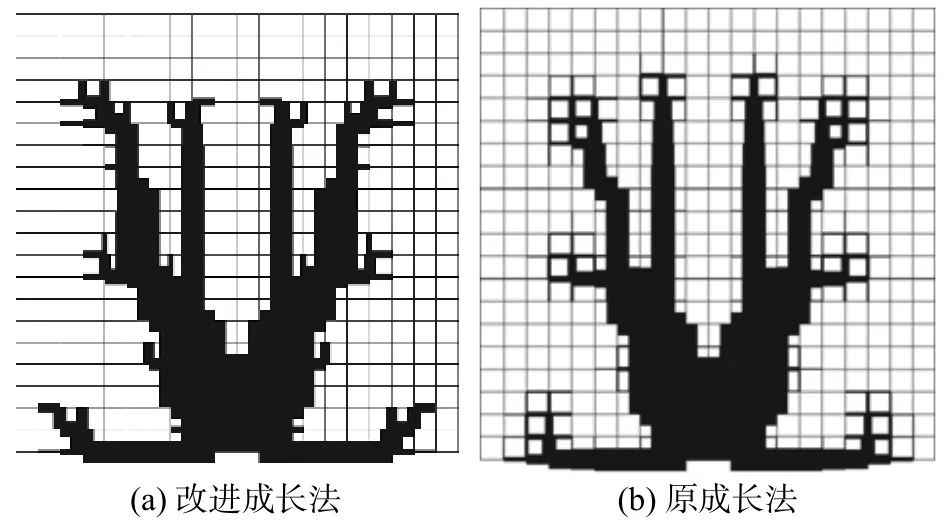
图17 不同方法拓扑形态Fig.17 Topology configuration by different methods

4 结 论

a.针对传热结构拓扑优化问题中普遍存在的棋盘格现象、无效细小分支过多等问题，在已有的传热结构自适应成长法基础上，提出了加入敏度过滤的两层顺序优化的改进成长法，解决了存在平行通道以及边界不清晰的问题。迭代公式以及敏度过滤有严格的数学推导，设计参数较少，迭代过程收敛性好。

b.与原成长法相比，改进成长法可用于各种复杂的热边界条件，尤其是热量不均匀分布情况下均能得到简单规则、对称且边界清晰的传热通道。同时，改进成长法所得到的热性能参数也大部分优于原成长法。此外，值得注意的是，不同边界条件下，加入密度梯度过滤技术的改进成长法得到的设计结果均最优。

c.加入 Density过滤的改进成长法与加入Density过滤的原成长法相比，热性能略有改善，拓扑形态更为清晰。