“输液装置”中液体是匀速流出吗？

(北京市第101中学,北京 100091)

医院输液装置大家应该都见到过,输液的过程中我们往往会看到药液一滴一滴是等时间间隔下落的．那么为什么液体会这样下落呢?

在人民教育出版社普通高中课程标准实验教科书物理必修2中,第5章“曲线运动”的第3节“实验:研究平抛运动”一节,介绍了描绘平抛物体运动的3个参考案例．其中第2个案例是利用倒置装水的饮料瓶喷出的细水柱显示平抛运动轨迹．书中给出的装置图如图1所示．这个装置和医院的输液装置类似,下面以图1装置为例进行分析,通过推导来理解液体匀速下落问题,从而类比理解输液装置中药液匀速下落问题．

图1所示装置模型平面图如图2所示．

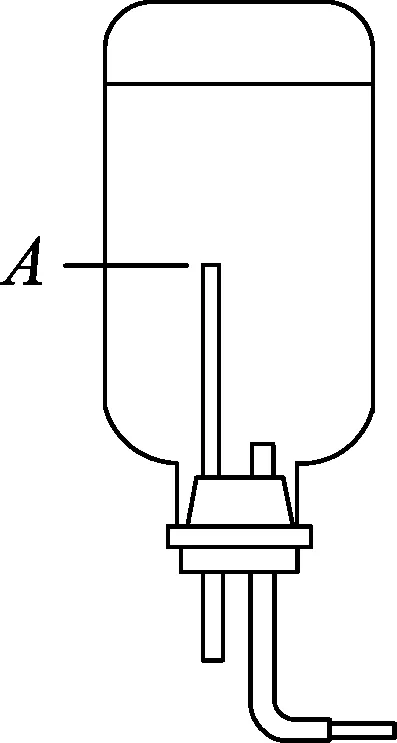
图1 图2

竖直的管子是和外界大气连通的小装置,设该装置在瓶内部最高处位置为A,瓶内液面到位置A的高度为hA,药液的密度为ρ液,设外界大气压强为p0,瓶内液面上方液体压强为p气,则

p0=p气+ρ液ghA,

即p气=p0-ρ液ghA.

如图2,瓶的内直径为d1,弯管的内直径为d2．液体流出过程中,相同时间内瓶内减少液体体积与从弯管内流出液体体积相同．某一时刻液体流出,瓶内液面会随之下降,该时刻液面下降速度设为v1,同时液体从弯管内流出时流速设为v2．则在极短时间Δt内,有

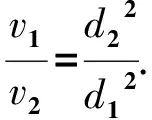
由功能关系可知,在Δt时间内,从弯管流出的液体体积ΔV可以等效理解为全部来自于瓶内液面下降部分对应液体．在Δt内,瓶内液面上方气体对下降液体ΔV做的功为

W气=p气ΔV=(p0-ρ液ghA)ΔV.

设瓶内液面位置A与弯管液体流出端高度差为H,相同时间内,外界大气、重力对流出液体做的功分别为

W大气=-p0ΔV，

WG=Δmg(hA+H)=ρ液ΔVg(hA+H).

忽略摩擦阻力及液体间粘滞阻力,研究Δt时间内流出的液体,合外力的总功为

W总=W气+W大气+WG=

(p0-ρ液ghA)ΔV-p0ΔV+ρ液ΔVg(hA+H)=

ρ液ΔVgH.

由动能定理可知

可得v22-v12=2gH.

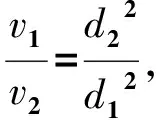
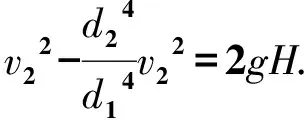
因此，液体从输液管中流出的速度为

从v2的推导结果可以看出,因为g、d1、d2和H都不变,所以弯管内液体流出速度不变,是匀速流出．同时也可以看出,当瓶内液面低于位置A时,H的值会随之减小,液体流速将变小．

如图2所示,弯管在瓶内与液体接触部分最高点位置为B点．A位置处压强一直等于外界大气压强,确保B位置处压强为一定值,这也是液体匀速流出的原因．若A比B位置低,随着瓶内液面下降,B位置处压强值会随之变化,液体将不会匀速流出．