变频供电异步电机端部绕组磁场分析

唐烈峥，阮江军，丁衡宇，黄 涛，刘海龙

(1.武汉大学 电气与自动化学院，武汉 430072；2国网湖南省电力检修公司，长沙 410004；3.国网江苏省电力工程咨询有限公司，南京 210000；4.中国船舶重工集团公司 第712研究所，武汉 430064)

0 引 言

异步电机端部漏磁会在绕组上产生时变电磁力，长期的电磁振动容易使绕组绝缘磨损和疲劳断裂[1-2]。而另一方面，随着电力电子和控制技术的进步，交流调速系统得到了快速发展，目前已逐步取代了传统的直流传动系统，其中变频调速是交流调速中应用最多的一种方式[3]。异步电机的变频调速虽然大大拓宽了其应用面，但也使定子电流及端部磁场中存在大量高次谐波分量，高次谐波的存在势必影响到端部绕组振动。

端部电磁场分析是振动计算的基础，常用的方法主要包括解析法和数值计算法。Lawrenson提出的方法是解析法中最为经典和具有代表性的[4]，其思路是将端部绕组分成许多短小的直载流导体，通过计算任意两段载流元之间的电磁力，并进行叠加得到绕组总体的电磁力分布，计算中将铁心结构简化为磁导率无穷大的理想磁镜面，并用附加的“气隙回转电流”补偿定转子的磁位差，此后，其他学者又进一步提出了分离变量法[5-6]、直接积分法[7]等有用方法，尽管很多文献报道了解析计算方法的研究，但由于难以准确描述端部复杂的结构，且不能考虑铁芯的饱和效应[8]，该方法计算精度较低。数值方法可以解决任意形状、任意类型的边界条件以及复杂的源分布问题，且计算成本低、效率高，已成为电机电磁场分析的主要方法。早期的研究由于受到计算能力的制约，主要采用准三维有限元法或有限差分法[1,9-12]，假设电磁场沿电机轴向按照正弦分布，并将定转子端部线圈电流以等效电流层代替，建立二维轴对称模型进行求解，但准三维有限元法难以考虑切向磁密，也不可能考虑齿部效应[13]。针对上述问题，许多研究者开始采用全三维有限元法计算端部绕组电磁场，Lin R在感应电机端部电磁场计算方面开展了大量工作[2,14-16]，文献[2]采用三维时谐场进行了异步电机端部绕组电磁分析。

针对变频器驱动异步电机的振动问题，丁衡宇等分析了电机本体所受的电磁激振力[18-20]，Chen F等计算了绕组在某一时刻的电磁力[21]，而未能进行瞬态分析，刘海龙等开展了变频异步电机底脚的振动试验研究[22]。

目前，国内外对变频器驱动异步电机的端部绕组磁场仿真分析鲜有研究。为此，本文首先采用二维场路耦合时步有限元法求解得到定子绕组电流，在此基础上通过三维瞬态磁场仿真分析端部绕组的漏磁，最后设计了与仿真模型一致的异步电机，并测量其端部绕组的磁密，仿真结果与试验测量值吻合良好，研究结果可为异步电机的优化设计提供一定参考。

1 理论基础

变频器驱动下异步电机端部绕组的电磁问题是一个电路、电磁场与运动系统等物理量相互耦合的非线性问题，直接求解难度较大。本文先采用二维场路耦合时步有限元法求得定子绕组电流，以此作为加载条件进行电机端部的三维磁场计算。由于变频器供电下电流和磁场中均存在大量高次谐波，时谐场只能考虑单次谐波的影响，因此文中均采用瞬态场进行求解。

1.1 二维场路耦合控制方程

1.1.1 场路直接耦合

电机本体的平面电磁场求解可以通过二维有限元法实现，定子绕组端部与转子端环等效为电阻、电感纳入路方程中，通过场-路方程相结合实现联立求解[23]，使模型可充分考虑转子绕组中的涡流、铁磁材料的非线性和端部参数对整体电磁场的影响。

由于定子绕组是绞线结构，忽略感应涡流，该区域满足下述电磁场方程[19]：

(1)

式中，A为矢量磁位；Js为源电流密度；υ为磁阻率，数值为磁导率的倒数。

考虑端部阻抗的定子绕组电压平衡方程为

(2)

式中，u为外施电压，R和Lσext分别为定子相绕组的总电阻和端部漏感，可用经典电机设计程序计算，由于端部不存在铁心，经典计算很准确；e为电极本体的定子感应电动势，可根据法拉第电磁感应定律按下式计算

(3)

式中，Leff为铁心有效长度；S为每相绕组电流区域面积；n为绕组区域剖分单元数，Aei为单元矢量磁位的平均值。

转子导条的涡流区域的控制方程为

(4)

式中，φ为电位；σ为电导率。

铁心与气隙非导电区域没有外加源项，电磁场方程如下：

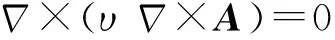
(5)

定子铁心外表面满足磁力线平行边界条件：

A=0

(6)

1.1.2 电磁场与运动问题间接耦合

电磁场间接耦合转子运动方程的基本思想是：固定时间步长，通过求解某一时步的电磁场获得电场转矩Tem，以此计算下一时刻电机转子的速度以及位置，如此进行下去便可得到场路耦合运动方程的求解，其中，转子的运动方程如下：

(7)

(8)

式中，Ω为转子角速度，Jm为转动惯量，TL为负载转矩。

1.2 磁场控制方程

以二维场路耦合时步有限元法得到的定子绕组电流作为加载条件，进行三维磁场计算，以矢量磁位为自由度进行求解，满足式(1)的控制方程。

2 仿真算例

2.1 电机模型

异步电机计算模型与文献[24]中所述一致，如图1所示。定子绕组采用三角形连接，电机结构参数如表1所示。逆变器采用双极性同步脉宽调制的控制方式，载波为三角波，频率fc设置为1650Hz；调制波为频率fr=50Hz的正弦波，调制系数H=0.8。

图1 异步电机计算模型

表1 电机主要结构参数

2.2 二维场路耦合时步有限元计算

场路耦合仿真中时间步长的设置对结果有较大影响，步长较长时会出现明显的三相不对称，且波形畸变严重，因此为提高计算精度，将步长取为0.00002s；为使电机尽快达到稳态，将转子的初始转速设置为2880r/min，仿真时长为0.8s。铁心为非线性铁磁材料DW465_50型硅钢片，在仿真中设置其磁化曲线，以充分考虑铁心饱和效应。定子A相绕组电流波形仿真结果如图2所示。

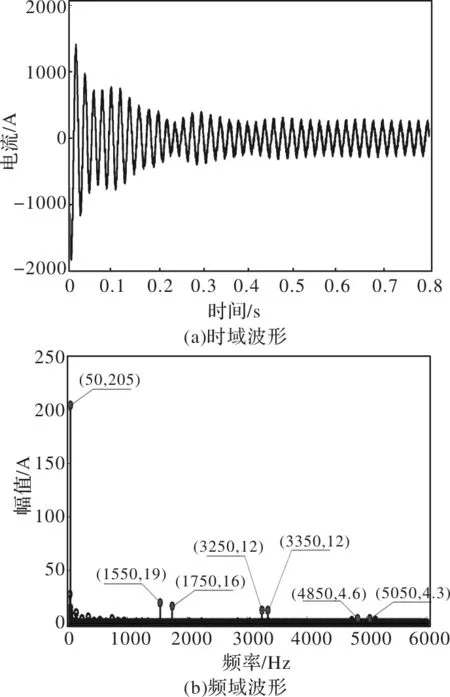
图2 定子A相绕组电流及其FFT

从图中可见，0.5s之后电机基本进入稳态运行；对定子A相电流进行快速傅里叶变换，主要谐波频率为1550、1750、3250、3350、4850和5050Hz，完全符合SPWM调制的频谱规律，可在一定程度上说明仿真的正确性。

2.3 三维磁场计算

以二维场路耦合时步有限元计算得到的定子绕组电流为加载条件，采用有限元法进行三维磁场求解，端部绕组计算模型如图3所示，考虑到分析难度，模型中忽略了转子铁心及导条涡流的影响，仅建立了定子铁心和绕组。仿真中时间步长设置为0.0002s，以充分考虑高次谐波的影响。

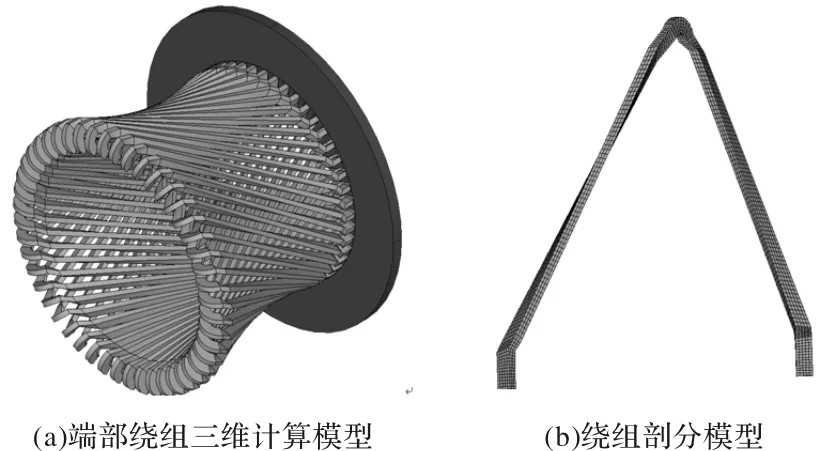
图3 计算模型及局部剖分图

仿真求解完后获取0.8s时刻定子绕组的电流密度分布如图4所示，可见电密加载方向以及大小及周期性均符合二极电机三相绕组电密的分布规律，从而进一步验证了加载方法的正确性。

图4 端部绕组电流密度

A相绕组中鼻子段某点各方向磁密的FFT如图5所示。受采样频率限制，最高频率只能分析到2500Hz，磁密主要高次谐波频率为1550Hz与1750Hz，由于磁密由电流分布决定，从理论上分析，两者应具有相同的特征频率，对比图2(b)和图5可知仿真结果与理论分析吻合较好。

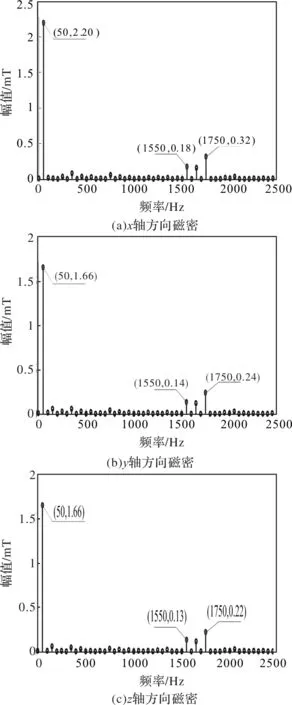
图5 定子A相绕组鼻子段磁密FFT

3 试验验证

3.1 试验布置

为验证所提仿真方法的有效性，设计了与仿真模型一致的三相鼠笼式异步电机，具体参数如2.1节所述，样机实物图如图6所示。

图6 测试电机实物图

定子电流由电流互感器获取。端部绕组磁密采用探测线圈的反电动势测量，本试验中采用了PCB板作为探测线圈，如图7(a)所示，并用环氧树脂板固定于端部绕组鼻子处，以测量3个不同方向的磁场，如图7(b)所示。

图7 用于磁场测量的探测线圈及其布置

3.2 测试结果

3.2.1 定子绕组电流

对测量的定子绕组A相电流进行快速傅里叶变换，结果如图8所示，主要谐波频率为1550、1750、3250和3350Hz。对比图2(a)可见，仿真得到的电流特征频率和基波幅值均与试验测量结果吻合良好。

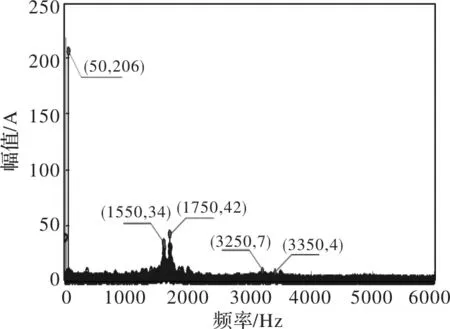
图8 定子绕组A相电流测量结果

3.2.2 端部绕组磁密

如前所述，磁密通过PCB线圈的反电动势间接测量，在正弦分析中，磁密的计算公式为

(9)

式中，Bm和Em分别为磁密和感应电动势的幅值，N和S为线圈匝数和截面积。

对测量到的感应电动势进行傅里叶变换，然后将每一频率分量的电动势代入式(9)即可得到磁密的频谱分布，结果如图9所示，主要特征频率均为1550 Hz和1750 Hz。对比图5可见，试验测量值与仿真结果在特征频率和幅值方面均较为接近，有效地验证了前述仿真模型的准确性。

图9 定子A相绕组鼻子段磁密测量结果

4 结 论

本文提出了变频器供电下异步电机端部绕组的磁场仿真方法，通过二维场路耦合时步有限元求得定子电流，在此基础上进行端部绕组的三维瞬态磁场分析。开展了模拟样机的试验测试，结果表明：仿真得到的定子电流及端部绕组鼻子段的磁密与试验测量结果和理论分析均吻合良好，为后续进一步研究变频器对端部绕组振动的影响提供了基础。