刷式密封泄漏特性数值方法研究与实验验证
孙 丹,丁海洋,李国勤,刘长胜,艾延廷
(1. 沈阳航空航天大学辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136;2. 沈阳鼓风机集团股份有限公司,沈阳 110142)
刷式密封是一种接触式动密封,具有优越的密封性能,已被广泛应用于汽轮机、燃气轮机和航空发动机等透平机械中[1-2],是传统迷宫密封简单实用的替代品。刷式密封流场复杂,准确计算刷式密封流场特性比较困难,开展刷式密封数值方法研究对准确计算刷式密封泄漏特性、优化刷式密封结构具有重要意义。
自20世纪80年代初至今,学者们先后提出了多种研究刷式密封泄漏流动特性的数值方法,包括等效厚度模型、多孔介质模型和流固耦合模型。Chupp等[3]最早提出了等效厚度模型模拟刷丝间的流动特性。王之栎、王宗根等[4]基于等效厚度模型研究了刷式密封的泄漏流动特性。Dogu等[5]将刷丝束处理为多孔介质,采用定常稳态求解方法,对刷式密封不同径向间隙下的泄漏特性进行了详细研究。Bayley[6]基于多孔介质模型,考虑了刷丝对流体的黏性阻力,对刷式密封泄漏特性进行了理论研究并与实验结果相比较。张元桥等[7]考虑了刷丝束与转子之间的摩擦热效应,利用多孔介质模型研究了压比、转速和后挡板保护高度对刷式密封泄漏特性的影响。孙丹等[8]基于流固耦合理论,采用数值方法分析了刷式密封的流场特性和刷丝在流场中的力学特性。研究结果表明,等效厚度模型是一种半经验公式,主要依据刷式密封实验数据统计分析,对实际情况的反映程度不足,因此很少被采用。多孔介质模型无法准确模拟刷丝束内部的实际流动情况,但计算相对简单,在精度要求不高的工程中应用广泛。流固耦合模型能够获得刷丝束内部流场细节,且能够模拟刷丝与流体之间的相互作用,计算精度较高。现有文献关于刷式密封泄漏流动特性的研究方法比较单一,综合分析不同数值方法的优缺点的文献较少,将数值方法与实验相验证的论文鲜有发表。
本文从数值方法和实验测试两方面研究了刷式密封泄漏流动特性,分别建立了多孔介质和考虑刷丝变形的流固耦合数值模型,设计搭建了刷式密封泄漏特性实验台,用实验方法研究了压比和密封间隙对泄漏特性的影响,对比验证了两种数值模型的求解结果,并研究了刷式密封的流场特性,旨在为准确预测刷式密封泄漏特性提供计算方法。
1 刷式密封泄漏流动特性数值方法
刷式密封三维模型如图1所示,刷丝束由柔软纤细的刷丝交错层叠排列而成,并沿着转子旋转方向与转子表面成一定角度,这使得刷丝对转子的瞬间径向变形或偏心运动具有更好的自适应性,能够保持良好的密封性能。
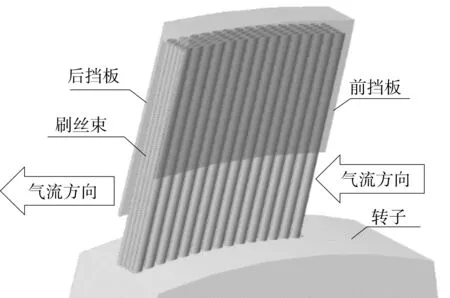
图1 刷式密封三维示意图
1.1 多孔介质模型
刷式密封中刷丝排列紧密且复杂,刷丝束中的流体流动非常复杂。在刷式密封泄漏特性的研究中,多孔介质模型是应用较广泛的理论模型。刷丝束内部流场的多孔介质理论模型与填充床渗透的流体流动相似,在刷丝束内部,流体的流动除了受到RANS方程中惯性阻力和黏性阻力的影响,还受到固体刷丝对流体的阻力作用,因此本文采用非线性Darcian多孔介质模型模拟刷丝束内部的流场特性,即在动量方程中加入黏性损失项和惯性损失项,按以下公式计算:
(1)
(2)
式中:Ai为黏性阻力系数矩阵;Bi为惯性阻力系数矩阵。
本文采用Ergun[9]方程推导刷丝束多孔介质区域的阻力系数,将轴向定义为z方向,将周向定义为n方向,将径向定义为m方向,则轴向、周向和径向黏性阻力系数分别为az、an和am,惯性阻力系数分别为bz、bn和bm,结合文献[10]推导出阻力系数计算公式如下:
(3)
由上式可以看出,刷丝束阻力系数由孔隙率和刷丝直径决定,其中刷丝束的孔隙率是指多孔介质区域中孔隙体积与总体积之比。本文通过对刷式密封几何结构的分析,结合文献[11]推导出了刷丝束孔隙率的计算公式:
(4)
式中:N为刷丝束密度;d为刷丝直径;w为刷丝束轴向厚度;φ为刷丝束倾斜角。
1.2 流固耦合模型
本文刷式密封流固耦合瞬态计算中,流体域满足的动量方程和连续方程如下[12-13]:
(5)

(6)
式中:ρ为密度;t为时间;U为速度矢量;u、v、w为速度矢量U在x、y、z方向的分量;Γ为平均有效扩散率;Su、Sv、Sw为动量守恒方程的广义源项。
刷丝束区域流场流动复杂,流场的湍流度和黏性系数体现出各项异性,需要对标准k-ε湍流模型进行修正,修正模型RNGk-ε如下[13]:
(7)
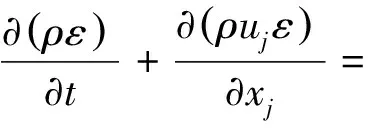
(8)
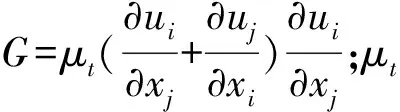
固体刷丝在非定常气动力作用下的瞬态响应可通过求解结构动力学方程获得[14],即:

流固耦合模型需通过流固耦合面对流体域和固体域进行数据信息传递。本文采用守恒差值法,在满足求解精度的要求、确保能量传递守恒的同时,使气动载荷和网格变形等信息通过流固耦合面进行信息交换与传递。通过传递函数[T]将刷丝网格位移Xs转换为流场的网格位移Xf,表达式如下[15]:
Xf=[T]Xs
(10)
在气动载荷作用下,刷丝与流体域耦合面应满足能量传递守恒要求,即:
(11)
由上可以得出载荷在两个物理场之间的传递关系:
Fs=[T]TFf
(12)
式中:Ff、Fs分别为作用在耦合面上的流体与刷丝载荷。
2 计算模型
2.1 求解模型
本文以密封实验台的迷宫与刷式混合式密封为研究对象,迷宫与刷式混合式密封二维结构示意图如图2所示,包括两组刷丝和三个迷宫密封齿,刷丝材料为镍基高温合金,弹性模量为213.7 GPa,泊松比为0.29。刷式密封的主要几何尺寸如表1所示。
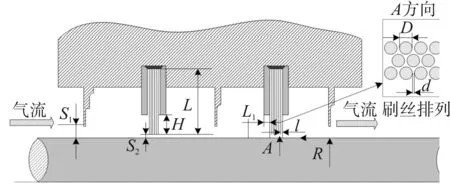
图2 密封实验件二维结构示意图
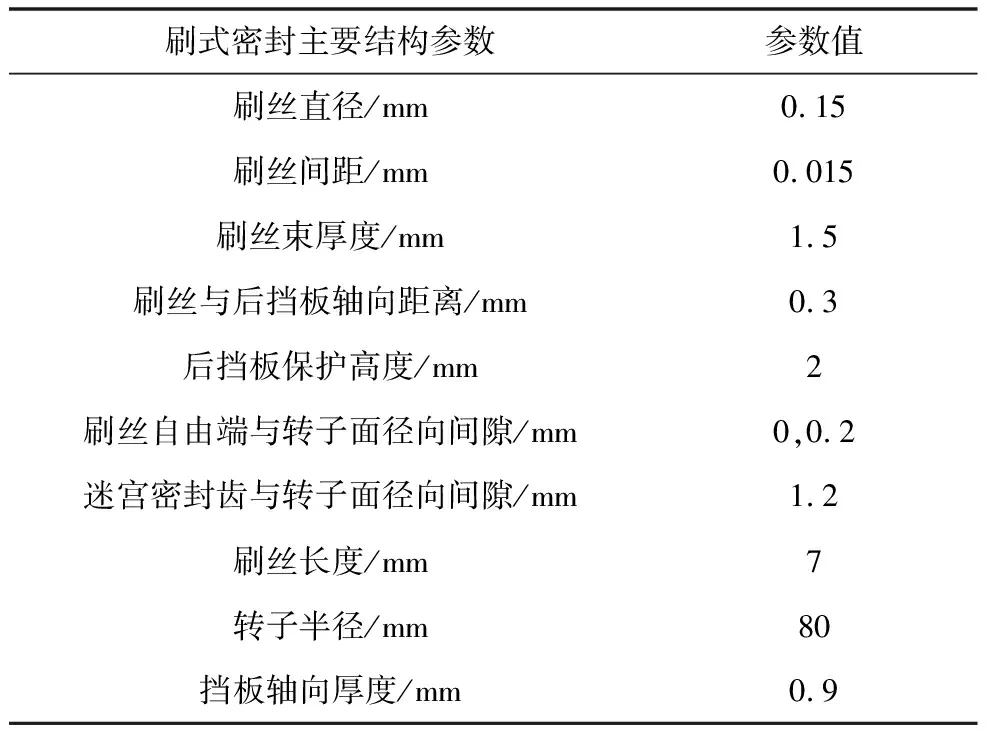
表1 刷式密封主要几何尺寸
2.2 网格划分
对于多孔介质刷式密封求解模型,由于采用多孔介质方法建模,迷宫与刷式混合式密封模型形状比较规则,可采用规则的四边形网格对其进行网格划分,将迷宫密封腔与刷丝束进行切分。刷丝束区域流体流动比较复杂,需对其进行网格加密,进行网格无关性验证之后,最终确定网格单元数为8万。
对于流固耦合刷式密封求解模型,考虑到刷式密封的周向对称性,为简化计算,采用最小周期性建模方法,对瞬态三维流固耦合模型进行网格划分,流体域网格分为迷宫密封腔和刷丝束两部分。图3为流固耦合模型的网格示意图,采用混合网格的方法,迷宫密封腔的流体采用规则的六面体网格。刷丝束区域流体流动比较复杂,采用对网格变形适应性更好的四面体网格。由于密封间隙较小,为准确捕捉气流通过密封间隙时的流体迹线,对刷丝端部与转子面间的密封间隙进行边界层网格加密处理。固体刷丝采用六面体网格。由于刷式密封内部流动较为复杂,网格质量对计算精度有一定影响,在进行了网格无关性验证后,最终确定流体域网格数为300万,固体域网格数为10万。
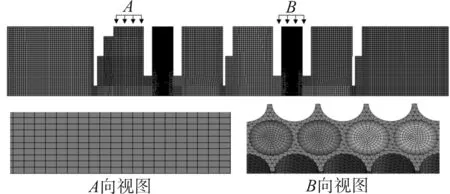
图3 流固耦合模型网格划分示意图
2.3 边界条件
图4给出了刷式密封多孔介质和流固耦合两种数值方法的边界条件示意图。流体介质为理想气体,采用等温模型,温度为常温298.15 K,刷丝排列方式为叉排交错式,则空气流动的雷诺数为[16]:
(13)
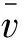

图4 刷式密封求解模型边界条件示意图
在刷式密封多孔介质模型中,将刷丝束部分设置成多孔介质区域,压力均为绝对压力,采用压力进口和压力出口边界条件,对流项和扩散项分别采用二阶迎风格式和中心差分格式。
在刷式密封流固耦合模型中,采用压力进口和压力出口边界条件,双向流固耦合面由固体耦合面和流体耦合面组成,固体域耦合面为刷丝的圆柱面和自由端底面,流体域耦合面为流体与固体耦合面接触的部分。对流固耦合面设置多场耦合可移动边界条件,周向对称壁面采用自由壁面边界条件,以便其可以随耦合面的变形而运动,转子面采用无滑移壁面边界条件。在非定常瞬态计算中,流体域与固体域的物理时间步长需保持一致,按照顺序求解的方法将定常稳态结果作为初始值,这有利于计算结果收敛。表2给出了求解模型的工况参数。

表2 密封模型工况参数
3 刷式密封泄漏特性实验验证
3.1 实验装置
本文搭建了刷式密封泄漏特性实验台,如图5所示。实验台由供气系统、密封系统、传动系统和润滑系统四部分组成。实验台的高压空气由螺杆式压缩机提供,存于储气罐中,最大可供压力为1 MPa。实验时由储气罐为密封气缸供气,采用中间进气、两端出气的方式,即从高压储气罐流出的高压气体经由分气缸分成四股气流,分别从气缸中部的上下、左右四个进气口径向供气。然后高压气体经过安装在气缸两端的两副相同的刷式密封件分别从气缸轴向两个端面流出。这一方面保证了进气均匀,另一方面避免了高压气流从气缸一端进气时产生的巨大轴向力,且确保气流全部经过两副刷式密封件泄漏,减小了实验误差。气缸内部结构如图6所示。

(a)密封装置气路示意图

(b)密封实验台
图6 气缸内部结构示意图
实验台转子长1 800 mm,实验段转子轴套直径为160.4 mm,转子转速在0~6 000 r/min范围间可调。实验件如图7所示,实验件内径为160.4 mm,轴向长度为26.94 mm,刷丝直径为0.15 mm,刷丝间隙为0.015 mm,刷丝长度为7 mm,后挡板保护高度为2 mm,刷丝束与后挡板轴向距离为0.3 mm。

图7 密封实验件实物图
3.2 实验结果与数值模型对比验证分析
刷丝自由端与转子间密封间隙分别设为0.2 mm和0 mm,图8和图9分别给出了不同压比下实验测得的泄漏量与两种数值方法计算的泄漏量随压比的变化曲线。可以看出,实验测得和流固耦合方法计算得到的刷式密封泄漏量随压比的增大而近似呈线性增大,而多孔介质方法在压比较大时,线性关系较弱。这是因为在大压比时,一方面刷丝束厚度有所降低,由公式(4)可以得出孔隙率会因此减小,从而使泄漏量稍微降低,另一方面是压比较大时,气流速度有所升高,雷诺数稍微增大,而计算采用层流模型,存在一定的误差,导致线性关系较弱。刷丝与转子面间隙为0.2 mm时泄漏量明显大于密封间隙为0 mm时的泄漏量,说明由密封间隙产生的直通效应是影响泄漏量的重要因素。
流固耦合模型的求解结果比多孔介质模型更贴近实验测量结果。多孔介质模型求解精度较低,主要原因是通过理论公式推导的孔隙率和阻力系数需要利用实验结果进行修正,具有求解模型的特定性。而流固耦合模型计算结果在大压比下与实验结果差距稍大,这是由于流固耦合模型在大压比下,刷丝之间相互接触,这减小了刷丝间隙,从而降低了流体有效流通面积,导致数值计算的泄漏量与实验测得的泄漏量差别稍大。但流固耦合模型能更准确地模拟流体在刷丝束间隙的流动细节。
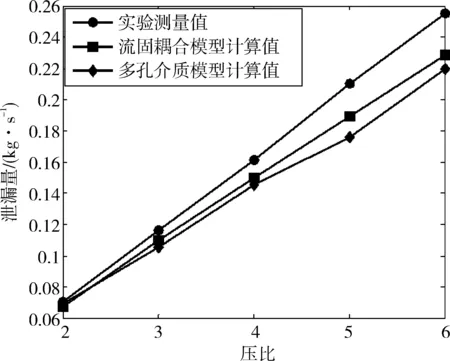
图8 0.2 mm间隙泄漏量随压比的变化规律

图9 0 mm间隙泄漏量随压比的变化规律
4 刷式密封流场特性分析
刷式密封刷丝在流场中受到高压气体的气流力作用,刷丝束内部流体迹线和压力分布非常复杂,而瞬态三维流固耦合模型可以较为逼真地模拟刷丝排列在流场中的运动轨迹以及流场特性。
4.1 刷式密封压力分布特性分析
图10给出了刷丝束密封间隙为0.2 mm、进口压力为0.5 MPa时,密封对称面的轴向压力分布图。从图10中可以看出,迷宫密封的密封腔内气流压力基本保持不变,压降主要发生在刷丝束区域。上游气流经过紧密排列的刷丝束,轴向压力逐渐降低,气流在后挡板内缘处加速膨胀,压力梯度较大,由压力分布情况可以发现,刷式密封中的刷丝束对提高密封的封严特性起到了重要作用。

图10 刷式密封压力分布
4.2 刷式密封速度分布特性分析
图11给出了刷丝束密封间隙为0.2 mm、进口压力为0.5 MPa时,刷式密封对称面的速度矢量分布图。由图11可以看出,在刷丝束区域,经过迷宫密封腔的气流进入刷丝间隙,流速从上游到下游逐渐增加。由于刷丝的阻滞作用,刷丝束根部气流流动非常微弱,在轴向压差作用下,下游流速增加较快,最大速度发生在刷丝自由端与转子间隙处,气流呈射流状喷出。此外,后挡板附近的气流径向速度急剧增大,在轴向速度的共同作用下,在后挡板内径转角处,气流大致以45°角呈射流状射出。

图11 刷式密封速度矢量分布图
4.3 轴向压力分布特性分析
为研究刷丝束内部的压力分布特性,分别定义了刷丝束的上端面、下端面、上游面和下游面。上端面为后挡板内径处刷丝束区域的周向环面,下端面为刷丝束自由端处的周向环面,上游面为前排刷丝沿周向旋转形成的圆环面,下游面为末排刷丝沿周向旋转形成的圆环面。
为了研究刷丝束内部压力分布随轴向位置的规律,将无量纲轴向相对位置a*定义如下:
(14)
式中:a为刷丝束轴向位置与刷丝束上游面的距离;h为刷丝束厚度。
图12和图13分别给出了刷丝束上端面和下端面沿轴向的压力分布特性曲线,可以看出上游气流在前挡板与刷丝之间的间隙处压力基本保持不变。由于上端面气流流动较微弱,气流经过紧密排列的刷丝束后轴向压力逐渐降低,后挡板和末排刷丝之间的间隙处压力梯度较小。下端面气流经过前排刷丝后压力迅速降低,压力梯度较大,之后以较小的压力梯度逐渐降低至下游值。

图12 刷丝束上端面轴向压力分布
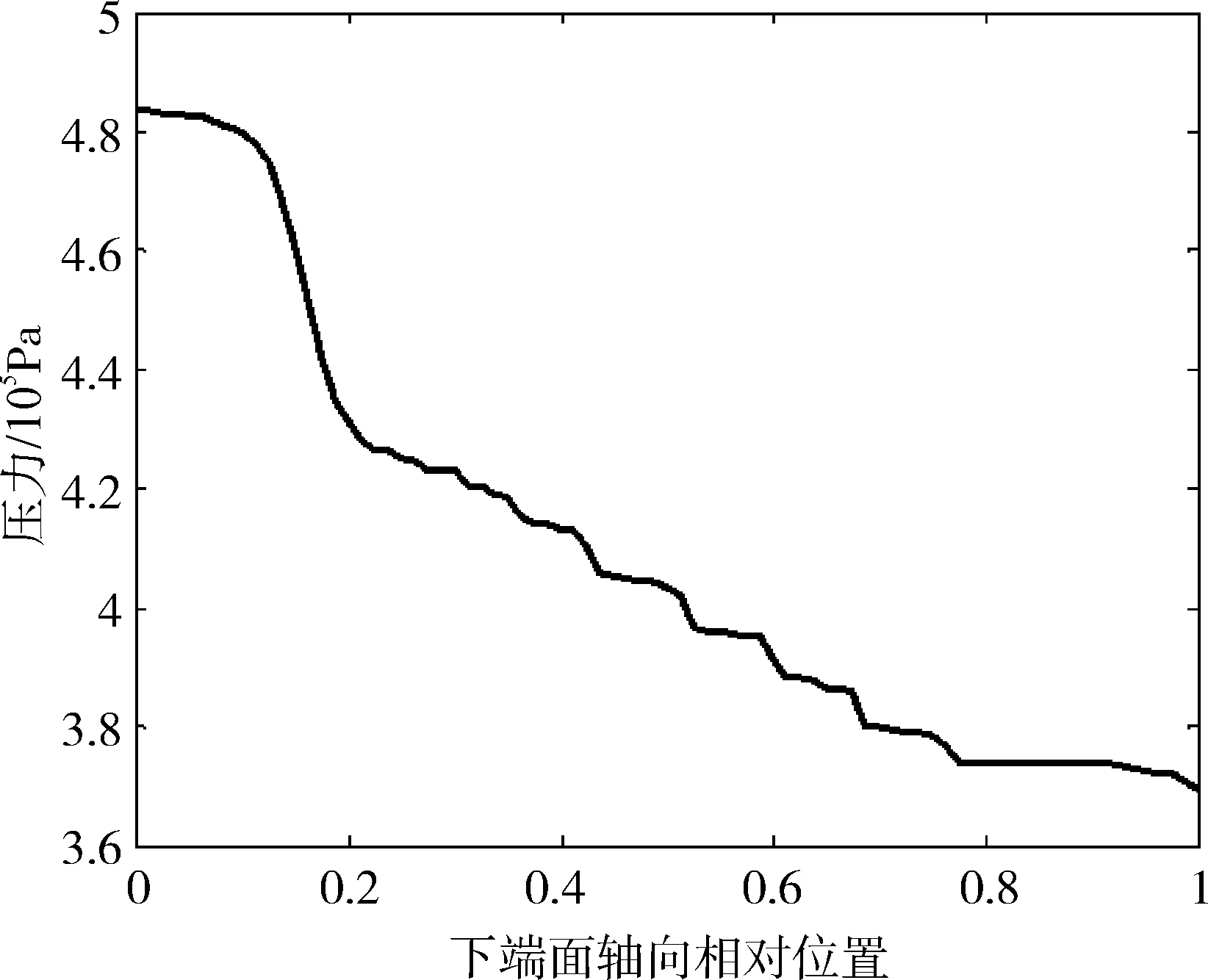
图13 刷丝束下端面轴向压力分布
4.4 径向压力分布特性分析
为了研究刷丝束内部压力分布随径向位置的规律,将无量纲径向相对位置r*定义如下:
(15)
式中:r为刷丝径向位置与刷丝自由端的距离;L为刷丝长度。
图14和图15分别给出了刷丝束上游面和下游面沿径向的压力分布特性曲线,可以看出,刷丝束径向压差沿轴向分布不均匀。在刷丝束的上游面,靠近刷丝自由端气流压力先急剧上升后迅速下降,在刷丝根部区域压力基本保持不变。下游面靠近刷丝自由端部分气流压力较小且基本保持不变,在后挡板内缘处压力急剧增大,径向压力梯度较大。径向压差的存在是刷丝产生“吹闭效应”的重要原因。

图14 刷丝束上游面径向压力分布
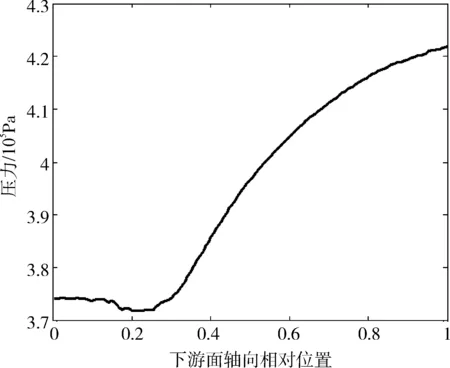
图15 刷丝束下游面径向压力分布
5 结 论
本文建立了稳态多孔介质模型和瞬态三维流固耦合模型,设计搭建了刷式密封泄漏特性实验台,通过实验研究了压比和密封间隙对刷式密封泄漏特性的影响规律,对比分析了两种数值方法的准确性,在此基础上,研究了刷式密封的流场特性,得出以下结论:
1)刷式密封的泄漏量随压比的增大而近似呈线性增大,随着密封间隙的增大,泄漏量显著增大,密封的直通效应是影响泄漏特性的重要原因。
2)对比分析了两种数值方法的准确性,流固耦合方法比多孔介质模型更贴近实验结果,但求解时间较长,多孔介质方法计算时间短,但需要在实验结果中对孔隙率和阻力系数进行修正,求解没有普适性。
3)刷丝束根部区域气流流动微弱,在轴向和径向气流的共同作用下,最大速度发生在下游密封间隙处和后挡板内缘转角处,大致以45°角呈射流状射出。
4)刷式密封压力降低主要发生在刷丝束内部,压力沿轴向逐渐降低,下端面前排刷丝束压力梯度较大。刷丝束上游面沿刷丝自由端至固定端,径向压力先急剧增大后显著减少,在刷丝束根部区域基本保持不变。下游面径向压力先基本不变后显著增大,径向压差的存在是产生“吹闭效应”的重要原因。

