拟牛顿布谷鸟混合算法∗
宋庆庆 贺兴时 郭 旭
(西安工程大学理学院 西安 710048)
1 引言
布谷鸟算法是2009年YANG模拟布谷鸟的寻窝产卵行为,提出了一种新的智能优化算法,该算法依赖于布谷鸟的巢寄生性和莱维飞行(Lévy flight)搜索原理[1]。布谷鸟算法(CS)有很好的全局搜索能力,但由于它的随机性强造成CS的局部搜索能力相对较弱,在后期优化效率地,因此需要进一步完善[2~4]。拟牛顿法是一种解决优化问题的有效方法,局部寻优能力强,但是拟牛顿算法对初值依赖性大,如果初始选的不合理,很可能造成算法不收敛[5]。目前拟牛顿法已经很好地与粒子群算法[6~7]、蝙蝠算法[8]遗传算法[9~10]、蚁群算法[11]结合。本文结合两算法的优点,在布谷鸟搜索后期可以加入拟牛顿法来优化布谷鸟算法的搜索性能,同时两算法又能相互克服缺陷。
2 拟牛顿布谷鸟算法
2.1 布谷鸟算法
在布谷鸟算法中的三点理想化条件:1)每只布谷鸟一次只产一个蛋,并且随机选择一个鸟窝来存放它;2)最好的鸟窝(解)将会被保留到下一代;3)可用鸟窝的数量n是固定的,鸟窝主人发现外来鸟蛋的概率是 Pα,其中 Pα∈[0,1]。在这种情况下,鸟窝主人可以将该鸟蛋丢弃,或者干脆放弃这个鸟窝,在新的地方重新建立一个鸟窝。在上边三个理想化条件下,布谷鸟根据Levy飞行进行搜索,步长更新公式为
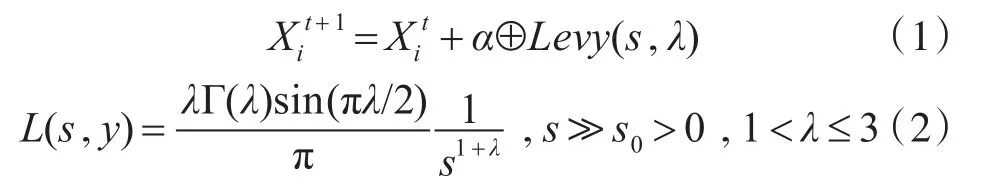
式(1)中⊕表示点对点乘法;式(2)s0表示初始步长。CS的具体操作步骤详见文献[2]。
2.2 拟牛顿法的步骤[12-13]
已知目标函数 f(X)及梯度g(X),终止准则ε。
2)计算搜索方向 dk。做直线搜索 f(X(k)+αkdk)=minf(X(k)+αkdk),求出步长因子 αk,并令xk+1=xk+αkdk。
3)判断是否满足终止条件,若满足则停止,否则转5)。
4)修正Bk产生Bk+1,使得拟牛顿条件成立。5)k=k+1,转至2)。
2.3 拟牛顿布谷鸟算法步骤
2)保留上一代最好鸟窝位置 fmin,利用式(1)、(2)对其他鸟窝进行位置更新,然后得到一组新的鸟窝位置Pt对这组鸟窝位置进行测试,与上一代鸟窝位置Pt-1=比较,让测试值较好的鸟窝位置替代测试值较差的鸟窝位置,从而得到一组较优的鸟窝位置
3)产生服从均匀分布的随机数 r∈(0,1),与布谷鸟的鸟蛋被鸟窝主人发现的概率Pα对比,保留P中发现概率较小的鸟窝位置,对概率较大的鸟窝位置进行随机改变,从而得到一组新的鸟窝位置。将这组鸟窝位置进行测试,与P=的每个鸟窝位置的测试值进行比较,用测试值较好的鸟窝位置替代测试值较差的鸟窝位置,从而得到当代全局最优鸟窝位置
4)以P′为初始位置,采用拟牛顿算法精确搜索目标位置,若达到终止条件,算法结束,并输出最优个体所在的位置,否则返回第2)步。
3 数值模拟
本文比较NQCS和CS对测试函数库中的8个测试函数[14~15]的优化性能。除了 Sphere是单峰函数以外,其他都为多峰函数,测试函数的最优值都为0,如表1所示。种群规模n=25,Pα=0.25,参数β=1.5 ,控制步长α取1,其他参数根据具体情况设定。

表1 测试函数
表2是NQCS和CS的测试结果表,表中的数据是在不同维度下计算函数的平均最优值、标准差、最大值、最小值。首先对与Cube函数、Himmelblau函数、Sphere函数来说NQCS的平均最优值远远小于CS并且计算精度上至少高出2个数量级,Zakharov函数和Zakharov函数甚至高出20个数量级,对于其他三个函数虽然不是很明显但也可看出NQCS的平均最优值结果优于CS的。其次在标准差方面,对于8个函数来说NQCS的标准差也都低于CS可以得出NQCS是比CS稳定的。接着是最大值最小值,发现仍然对于Cube函数、Himmelblau函数、Zakharov函数、Sphere函数、Schwefel 2.4函数NQCS的最值明显小于CS的最值,Cosine Mixture函数、Quintic函数、Ackley函数的最值也是NQCS较小。因此可以初步得出在计算精度上NQCS是优于CS的。
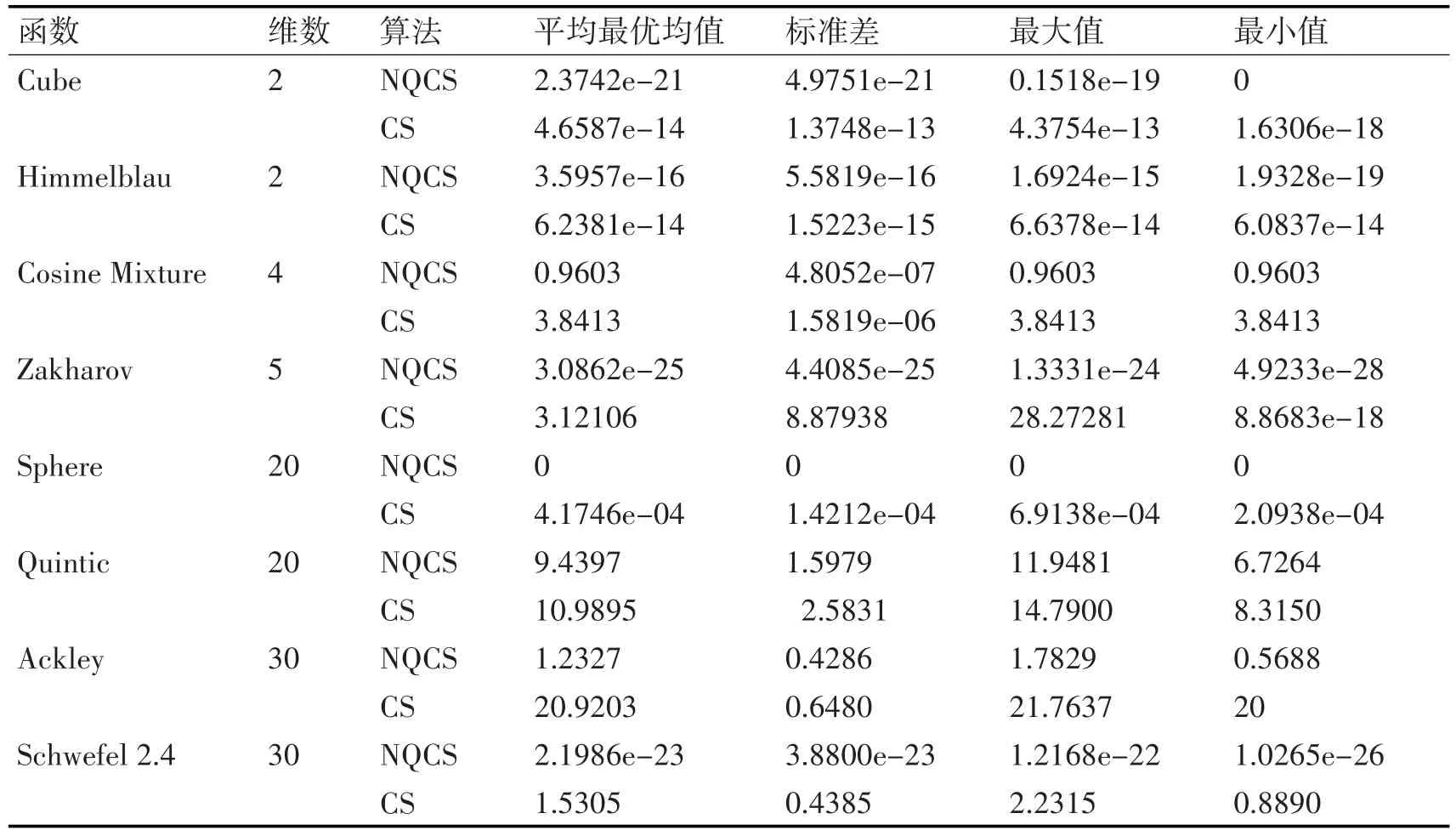
表2 两种算法的测试结果
两个算法在8个测试函数上均独立运行20次,因而在每个测试函数上,每种算法都有20个样本。采用T检验比较分析NQCS和CS的性能。本实验的T检验的自由度为38,显著水平为0.05。P值代表显著性水平,当P小于0.05时,表示NQCS显著优于CS,反之则不显著。
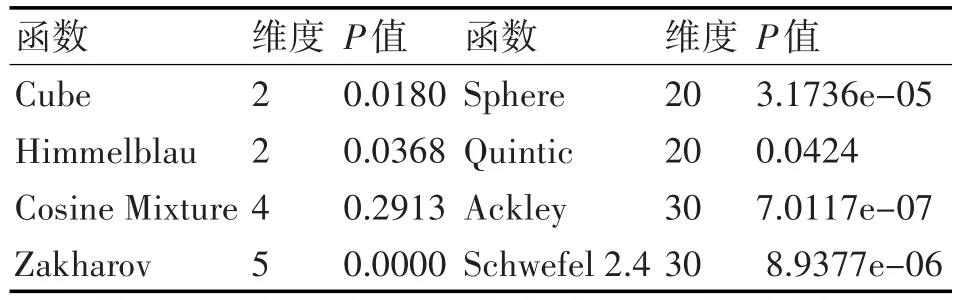
表3 两算法的T检验结果
从表3中NQCS和CS的T检验结果可以看出Cube函数、Zakharov函数、Sphere函数、Quintic函数、Ackley函数、Schwefel 2.4函数P值小于0.01,表明NQCS非常显著的优于CS。Himmelblau函数的P值大于0.01小于0.05,表明NQCS显著优于CS。Cosine Mixture函数的P值大于0.05表明在统计学角度上NQCS是不显著优于CS的。
因此综上所述,NQCS在大部分测试函数上显著优于CS。
4 结语
本文拟牛顿算法和布谷鸟算法相结合,建立了一种混合算法NQCS。先采用CS为BFGS提供一个较好的初始点,然后再用BFGS更进一步搜寻局部精确解。这样既可以避免CS局部精细搜索能力差,又能弥补拟牛顿算法对初值敏感的不足。通过8个基准函数测试其性能,实验结果表明NQCS明显比CS具有更高的收敛精度和更好的全局最优值。

